基于響應面法的印制電路板組件有限元模型修正

基于響應面法的印制電路板組件有限元模型修正

王開山，李傳日，龐月嬋，郭恒暉

(北京航空航天大學可靠性與系統工程學院，北京100191)

摘要：在將印制電路板及元器件材料視為正交各向異性前提下，提出基于響應面法的印制電路板組件(Printed Circuit Board Assembly，PCBA)有限元模型修正法。利用相關性分析篩選出對PCBA模態頻率影響較大參數作為修正參數；據修正參數數目選擇合適的試驗設計獲取樣本點，構造多項式響應面模型；通過最小二乘法確定多項式系數并檢驗響應面擬合精度；用響應面計算結果與模態試驗結果誤差絕對值構造目標函數；通過多目標遺傳算法(MOGA)迭代計算獲得優化修正參數并代入有限元模型獲得修正模型。以某航空電子產品某PCBA為案例，對比修正前后各階模態頻率與試驗值誤差。結果表明，修正后模型各階模態頻率與試驗值相對誤差均明顯減小，驗證該方法對PCBA模型修正的有效性。

關鍵詞：各向異性；印制電路板組件；模型修正；相關性分析；響應面法；優化求解

中圖分類號:V414；TB330.1；TH113文獻標志碼：A

基金項目：國家自然科學基金資助項目(51175086)；福建省自然科學

收稿日期：2014-08-19修改稿收到日期：2014-10-23

Finite element model updating of printed circuit board assembly based on response surface methodology

WANGKai-shan,LIChuan-ri,PANGYue-chan,GUOHeng-hui(Beijing University of Aeronautics and Astronautics, School of Reliability and Systems Engineering，Beijing 100191, China)

Abstract:On the premise of taking the materials of the printed circuit board and its components as orthotropic, a method based on response surface was proposed to update the finite element model(FEM) of printed circuit board assembly(PCBA). The parameters which have great influence on the modal frequencies of PCBA were screened out and taken as the updating parameters by correlation analysis. The sample points were acquired by using an appropriate experimental design according to the number of the updating parameters to construct a polynomial response surface model. The least squares method was used to determine the polynomial coefficients and then to test the fitting accuracy of response surface. The absolute value of error between the result of the calculated response surface and that of an actual test was taken as an objective function. The optimized parameters were obtained taking advantage of the iterative calculation of the multiple objectives genetic algorithm (MOGA). The updated model was then obtained by substituting the optimized parameters into the non-updated FEM. Taking the PCBA of an aircraft electronic product as an example, the comparison between the modal frequencies of non-updated and updated FEM shows that the relative error of modal frequencies of the updated FEM to the actual test is obviously reduced and thus verifies the effectiveness of the model updating methodology suggested.

Key words:orthotropic; printed circuit board assembly(PCBA); model updating; correlation analysis; response surface methodology; optimization

振動會造成電子產品發生故障，尤其對機載電子產品，在壽命周期內需經受嚴酷的動力學環境，致故障更嚴重。為提高電子產品可靠性，須增強其抗振能力。有限元仿真因周期短、成本低等優勢已成為產品動力學分析的重要方法。對產品進行有限元仿真前需進行實物模態試驗作為仿真結果檢驗及模型修正標準。模態試驗時通常無法將PCB與元器件分開，只能對裝配體即PCBA進行整體試驗，使對應的PCBA有限元模型精度非常重要。

工程實踐中通常按各向同性給出PCB及元器件材料參數的經驗值[1-2]，但其仿真結果往往與模態試驗結果相差較多。因不同PCB板鋪層、工藝不同材料參數有差異；元器件材料參數因器件種類、封裝不同存在較大不同。即使同一塊PCB板也會因不同位置電路、通孔分布表現出材料參數的各向異性。為提高仿真精度，需將PCB及元器件材料視為各向異性對PCBA模型進行修正。

響應面法因具有易于迭代、優化特點廣泛用于結構優化設計。因此利用該方法進行動力學模型修正的研究成為熱點。鮑諾等[3]利用響應面法對歐洲航空科技組織的基準GARTEUR飛機模型進行修正。費慶國等[4]在響應面方法基礎上結合軟件MATLAB與ANSYS的集成實現鋼架結構模型修正。常濤等[5]利用響應面法對PCB裸板進行模型修正。而對工程遇到最多的PCBA模型修正研究尚處空白。本文在響應面方法基礎上，結合相關性分析及優化算法給出PCBA模型修正的一般流程及方法原理，并以某航空電子產品某PCBA為算例，驗證該方法的合理性及有效性。

1PCBA模型修正流程

PCBA有限元模型修正的一般流程見圖1。包括參數篩選、響應面模型構建及優化求解三大模塊。所涉關鍵技術方法有相關性分析、試驗設計、響應面擬合、擬合優度檢驗及遺傳算法等。

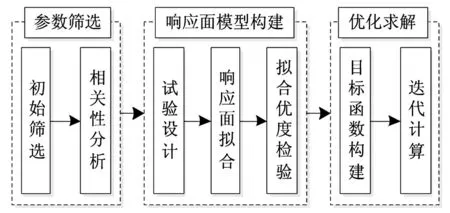
圖1　PCBA模型修正流程 Fig.1 The model updatingprocess of the PCBA

2修正參數篩選

2.1參數初始篩選

對輸出響應量，因模態頻率易測量、精度高，故本文選前三階模態頻率作為響應特征量。影響PCBA模態頻率因素有模型的幾何尺寸參數、密度及材料參數[6]。幾何參數、密度易控制及測量，波動性不大；材料參數由鋪層、工藝、電路分布、通孔分布等不同導致的不確定性較大為造成PCBA動力學仿真結果不準確的主要因素[7-8]。據此將PCB及元器件材料參數作為初始篩選參數，包括PCB、元器件各自三個軸向彈性模量、平面泊松比及平面剪切模量計18個參數。并將其視為正交各向異性；對元器件，封裝種類不同其材料參數亦不同。本文為簡化僅考慮器件均塑料封裝情況，將所有元器件視為同種材料進行處理。

2.2相關性分析

初始篩選的18個參數均波動性較大，但并非所有參數均對輸出參數(前三階模態頻率)產生較大影響，需定量相關性分析,篩選對模態頻率影響大的參數。Speraman等級相關系數可從全局角度考量輸入對輸出的相關性，計算式為

(1)

式中：R(xi)為將不確定參數抽樣值(x1,x2,…,xn)按升序或降序排列時xi的排序號；R(yi)為將響應計算值(y1,y2,…,yn)按升序或降序排列時yi的排序號；n為抽樣次數。

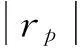
3響應面模型構建

多項式響應面為用統計學回歸分析進行函數擬合的近似方法，通過確定性試驗設計擬合出響應面函數近似模擬真實輸入、輸出間隱式關系，使系統分析可建立在響應面函數上。與一次、高次(三次及以上)響應面相比，二次響應面能較權衡近似精度與計算量間的矛盾，故工程中應用較廣[11-13]。

3.1試驗設計

基于多元線性回歸的多項式響應面需數據樣本，構造的樣本試驗點在修正參數區間內分布對響應面近似精度影響較大。全因子設計將每個因素的不同水平組合均進行一次試驗，因該方法為因子與水平的完全組合，結果真實可靠；但計算量過大只適合因素較少情況[14]。因素較多時常采用中心點復合設計、Box-Behnken Design及D-最優設計等，均能用最少試驗樣本點獲得理想的響應面模型[15]。

3.2響應面擬合

PCBA前n階仿真模態頻率y為因變量，xi(i=1,2,…,k，k)為修正參數個數。多項式響應面函數表示為

(2)

式中：xi∈[xil,xiu]，xil,xiu分別為修正參數xi取值上下限；β0,βi,βij,βii為待定系數[16-17]。

可將試驗樣本點代入函數方程用最小二乘法估計多項式系數β0,βi,βij,βii。

3.3擬合優度檢驗

利用相對均方根誤差RMSF及R2判斷系數法可定量檢驗響應面精度，計算式為

(3)

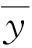
4優化求解

模型修正問題轉化為多目標優化問題，即

(4)

采用多目標遺傳算法(MOGA)對構建的目標函數進行迭代計算獲得修正后參數，代入有限元模型計算可得修正后模型。

5案例分析

所選案例為某航空電子產品中某PCBA，實物見圖2(a)。在不影響產品動力學特性前提下，在CAD軟件中按原則對該PCBA的數字樣機進行必要簡化，見圖2(b)。遵循原則為，①去掉尺寸較小的孔；②去掉尺寸較小的凸臺；③去掉尺寸較小的圓角；④去掉不必要的倒角；⑤適當省略對整體PCBA模態特性影響較小的小體積及小質量器件。

圖2　PCBA實物及有限元模型 Fig.2 The physical model and finite element modelof the PCBA

5.1模態試驗及初始仿真

對PCBA進行自由狀態模態試驗，提取前三階頻率；在ANSYS中按各向同性給出PCB及元器件材料參數的經驗值，邊界條件設為自由狀態，選擇合適的網格劃分形式劃分網格后進行初始仿真，初始材料參數見表1。初始仿真與模態試驗結果對比見表2。由表2看出，初始仿真與試驗結果誤差較大，需進一步修正。

表1　初始材料參數

表2　初始仿真與試驗結果對比

5.2參數篩選

將PCB與元器件材料視為正交各向異性，計算前三階模態頻率與18個參數的Speraman等級相關系數，結果見圖3。由圖3看出，前三階模態頻率與印制電路板Y向彈性模量P-Ey、印制電路板XY平面的剪切模量P-σxy及元器件XY平面剪切模量C-σxy的相關性超過0.3，因此將其確定為修正參數。

圖3　相關性分析結果 Fig.3 The results of correlation analysis

5.3響應面模型構建

修正參數僅3個，用全因子方法進行試驗設計。每個因素取3個水平，所選水平值需能覆蓋其整個區間，3個因素所選3個水平為：P-Ey為6.5E+9、8.75E+9、1.1E+10；P-σxy為1E+9、2.648E+9、4.297E+9；C-σxy為3E+8、2.45E+9、4.6E+9；共進行27次有限元仿真試驗，每組試驗只改變修正參數值，控制邊界條件及網格劃分等設置條件與初始仿真一致，即邊界條件均為自由狀態，網格數均為8 244；將試驗所得樣本點歸一化后代入響應面方程，用最小二乘法估計出多項式系數。構建的前三階響應面方程為

(5)

取13個樣本點進行擬合優度檢驗，計算R2判斷系數及相對均方RMSE，結果見表3。R2趨近1表明響應面與真值之間差異程度小；RMSE趨近0表明響應面精度高。

表3　R 2及RMSE檢驗

5.4優化求解

用前三階模態頻率與試驗值的誤差絕對值構造三個目標函數，采用MOGA遺傳算法迭代計算獲得優化修正后參數，并與初始參數對比見表4。將修正后參數代入有限元模型計算獲得修正后模型，仿真與試驗值對比見表5。

表4　模型修正前后參數對比

表5　模型修正后仿真與試驗結果對比

模型修正前后模態頻率相對誤差對比見表6，MAC值對比見表7。由表6知，修正后各階仿真模態頻率與模態試驗各階結果相對誤差均明顯減小。由表7知，修正后各階MAC值均較修正更接近1，從而驗證基于響應面法對PCBA模型修正的合理性及有效性。

表6　模型修正前后相對誤差對比

表7　模型修正前后MAC值對比

6結論

(1)基于相關性分析、響應面擬合及優化求解相結合方法可準確對PCBA模型進行修正，有效提高模型精度；用響應面替代真實模型進行動力學模型修正可避免多次調用有限元程序，提高分析效率。

(2)本文將所有元器件按同一種材料處理，但實際上不同種類元器件材料參數差異較大，可對不同種類元器件分別定義為不同變量進行分析修正效果可能更好。

參考文獻

[1]王紅芳，趙玫．基于動態特性的印制板結構改進[J]．振動與沖擊,2000,19(1):49-51.

WANG Hong-fang, ZHAO Mei. The structure improvements based on the dynamic characteristics of the printed circuit board[J]. Journal of Vibration and Shock, 2000, 19(1): 49-51.

[2]楊宇軍,葉松林,游少雄,等．插板式PCB的內置式減振設計方法及其PSD動力學仿真[J]．振動與沖擊，2007，26(2)：39-42.

YANG Yu-jun, YE Song-lin, YOU Shao-xiong, et al. The vibration damping design method of PCB and its PSD dynamics simulation[J]. Journal of Vibration and Shock, 2007, 26(2): 39-42.

[3]鮑諾,王春潔,趙軍鵬,等．基于響應面法的結構動力學模型修正[J]．振動與沖擊,2013,32(16):30-34.

BAO Nuo,WANG Chun-jie,ZHAO Jun-peng,et al.The structural dynamics model updating based on response surface methodology[J].Journal of Vibration and Shock,2013,32(16):30-34.

[4]費慶國,韓曉林,蘇鶴玲．響應面有限元模型修正的實現與應用[J]．振動、測試與診斷,2010,30(2):132-134.

FEI Qing-guo, HAN Xiao-lin，SU He-ling. The implementation and application of finite element model updating based on response surface[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(2): 132-134.

[5]常濤,郭勤濤,張保強．應用模型修正方法的印制電路板參數識別[J]．振動、測試與診斷，2013，33(3)：111-116.

CHANG Tao, GUO Qin-tao, ZHANG Bao-qiang. Parameter identification of printed circuit board using model correction method[J]. Journal of Vibration，Measurement & Diagnosis, 2013,33(3):111-116．

[6]Heinonen O, Pajunen S. Optimal design of stiffened plate using metamodeling techniques[J]. Journal of Structural Mechanics, 2011, 44(3): 218-230.

[7]Friswell M I, Mottershead J E, Ahmadian H. Combining subset selection and parameter constrants in model updating[J]. Journal of Vibration and Acoustics, 1998, 120(4): 854-859.

[8]Friswell M I, Garvey S D, Penny J E T. The convergence of the iterated IRS method[J]. Journal of Sound and Vibration, 1998, 211(1): 123-132.

[9]莊楚強．應用數理統計基礎(4版)[M]．廣州:華南理工大學出版社,1992.

[10]Dougles C. Montgomery design and analysis of experiments [M]. John Wiley & Sons, Tnc, 2008.

[11]郭勤濤,張令彌,費慶國．用于確定性計算仿真的響應面法及其試驗設計研究[J]．航空學報,2006,27(1): 55-61.

GUO Qin-tao, ZHANG Ling-mi, FEI Qing-guo. Response surface method and its experimental design for deterministic computer simulation[J]. Journal of Aeronautics,2006,27(1):55-61.

[12]宗周紅,高銘霖,夏樟華．基于健康監測的連續剛構橋有限元模型確認(I)-基于響應面法的有限元模型修正[J]．土木工程學報,2011,44(2)：90-98.

ZONG Zhou-hong, GAO Ming-lin, XIA Zhang-hua. The finite element model validation of continuous rigid frame bridge based on health monitoring(I)-the finite element model updating based on response surface[J]. China Civil Engineering Journal, 2011, 44(2): 90-98.

[13]Kwon J H, Hwang S M, Lee C M, et al. Application of response surface methodology in microspeaker design used in mobile phones[J]. Institute of Electrical and Electronics Engineers Transactions on Magnetics, 2009, 45(10): 4550-4553.

[14]Montgomery D C. Design and analysis of experiments [M]. John Wiley & Sons, Tnc, 2008.

[15]Montgomery D C．試驗設計與分析[M]．北京：中國統計出版社,1998:563-575.

[16]費慶國,張令彌,李愛群,等．基于統計分析技術的有限元模型修正研究[J]．振動與沖擊,2005,24(3):23-26.

FEI Qing-guo, ZHANG Ling-mi, LI Ai-qun, et al. The finite element model updating based on statistical analysis techniques[J]. Journal of Vibration and Shock,2005,24(3): 23-26.

[17]費慶國，韓曉林，蘇鶴玲．響應面有限元模型修正的實現與應用[J]．振動、測試與診斷,2010,30(2)：132-134.

FEI Qing-guo, HAN Xiao-lin, SU He-ling. The implementation and application of finite element model updating based on response surface[J]. Journal of Vibration, Measurement & Diagnosis,2010,30(2):132-134.

第一作者鄭書河男，博士，副教授，1976年10月生