基于PHD的多目標檢測前跟蹤改進方法?

柳 超,關 鍵,黃 勇,王國慶

(1.海軍航空工程學院電子信息工程系,山東煙臺264001;

2.中國人民解放軍92853部隊,遼寧葫蘆島125106;

3.海軍航空工程學院信息融合技術研究所,山東煙臺264001)

0 引言

多目標檢測前跟蹤問題是當前微弱目標檢測和數據融合領域研究的熱點和難點問題,其難點主要體現在多目標環境下往往需要復雜的數據關聯[1-2]。文獻[3]提出了一種基于粒子濾波的多目標檢測前跟蹤方法,雖然可以避免數據關聯,但是當目標數大于2個時,狀態轉移矩陣的討論和計算都變得非常復雜,很難推廣應用到目標數更多的場合。

近年來,基于有限集統計學理論(Finite Set Statistics Theory,FISST)的多傳感器多目標跟蹤方法得到了快速發展。這種方法通過隨機有限集建模并利用集合的微積分運算推導出最優多目標貝葉斯濾波器,成功地規避了數據關聯所帶來的困難和麻煩。2003年,Mahler提出了概率假設密度(Probability Hypothesis Density,PHD)濾波器[4],其實質是隨機集多目標狀態在其后驗概率密度下的一階矩,相比最優多目標貝葉斯濾波器,PHD濾波器的運算復雜度有很大降低;之后,Vo給出了PHD濾波器的兩種收斂實現方式：序貫蒙特卡洛PHD[5],也稱概率假設密度粒子濾波(Particle Filter PHD,PF-PHD),和高斯混合PHD[6](Gaussian Mixture PHD,GM-PHD),使得基于FISST的多目標跟蹤方法向工程應用邁進了一大步。

在PHD的檢測前跟蹤應用方面,Punithakumar K在文獻[7]中首次將PF-PHD應用于紅外圖像的多目標TBD中,提出了PF-PHD-TBD方法。該方法引入多目標跟蹤的思想,建立起目標的運動模型和傳感器測量模型,在信噪比較低的情況下取得了較好的效果,證明了PFPHD-TBD方法在多個微弱目標檢測及跟蹤方面的有效性。由于該方法對目標數目和狀態的估計精度還不夠高,文獻[8-12]等又各自從不同角度對PF-PHD-TBD算法進行改進,并分別取得了一定效果。

目前,PF-PHD-TBD性能表現不佳的原因,除了信號層觀測模型建立不準確導致的測量值不滿足理論假設外,其僅僅采用基本粒子濾波實現對PHD近似也是一個重要原因。尤其當目標維數較高時,不僅計算復雜,而且對權重起作用的因素往往只是與測量值有直接關聯的狀態矢量,與測量無關的狀態矢量沒有被充分利用,由此導致粒子權重之和即目標的數目估計不準確,從而造成聚類不穩定和狀態估計精度低等問題。Rao-Blackwellised粒子濾波(RBPF)[13-15]被認為是通過邊緣化線性變量減少狀態空間維數的有效辦法。與基本粒子濾波相比,它將目標的狀態空間進行降維分解,分別運用線性與非線性濾波器進行處理,顯著降低了粒子狀態維數,減少了所需粒子數和計算量,并且充分利用各維狀態矢量的信息,提高了狀態估計精度。在RBPF濾波與隨機有限集結合方面,文獻[16-17]分別作出了嘗試,將RBPF應用于多目標的跟蹤,取得了不錯的效果,但是目前尚未見到RBPF應用于隨機集多目標檢測前跟蹤的相關文獻。因此,本文提出一種結合RBPF的PFPHD-TBD方法,用于改進隨機集框架下多目標檢測前跟蹤的性能。

1 狀態模型及觀測模型建立

1.1 目標運動模型

假設在k時刻目標的數目為N k,目標的狀態為5維向量：

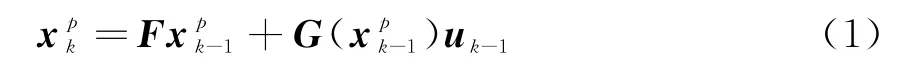
式中,F為狀態轉移矩陣,u k為獨立的高斯白噪聲。u k～N(0,Q k),其中Q k為噪聲協方差。包含所有目標的觀測集合為

1.2 傳感器觀測模型

將回波信號表示為距離-多普勒-方位域的觀測數據。設單元(i,j,l)(i=1,…,Nr,j=1,…,Nd,l=1,…,Nb,其中Nr,Nd和Nb分別表示距離、多普勒和方位的維數)處的功率觀測值z(i,j,l)k為

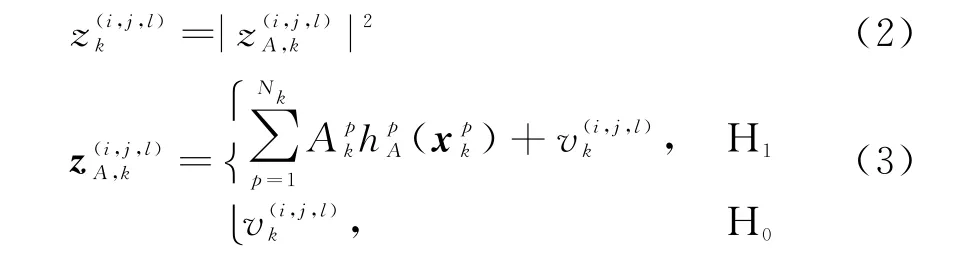
式中,H1,H0分別表示存在和不存在目標,為(i,j,l)處的觀測噪聲。若以,…,Nr,j=1,…,Nd,l=1,…,Nb}表示k時刻的所有量測,則聯合似然函數為

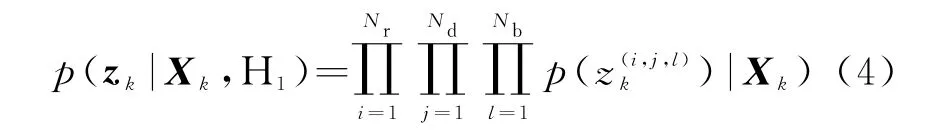
如果用Cr(s k),Cd(s k),Cb(s k)分別表示目標實際影響到的區域,則聯合似然比的計算可簡化為

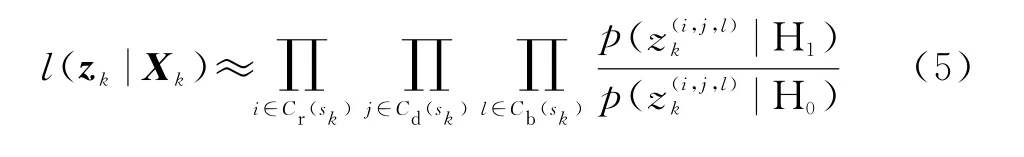
2 PF-PHD-TBD算法

在k-1時刻用一組有權重的粒子來表示目標的后驗概率分布：

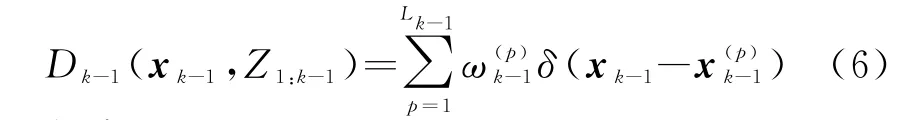
狀態預測：

設k-1時刻有L k-1個粒子,k時刻新生粒子的采樣數為J k,則預測密度為

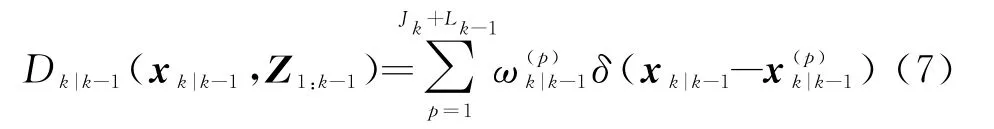
其中,對于存活粒子p=1,2,…,L k-1,按下式采樣：

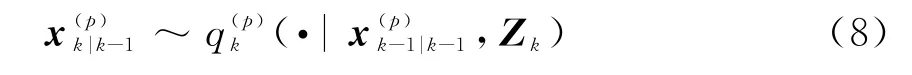
并計算其權重為

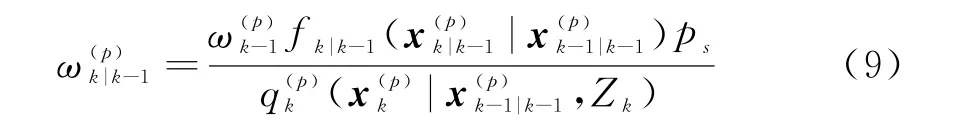
對于新生粒子p=L k-1+1,…,L k-1+J k,按下式采樣：

并計算其權重為

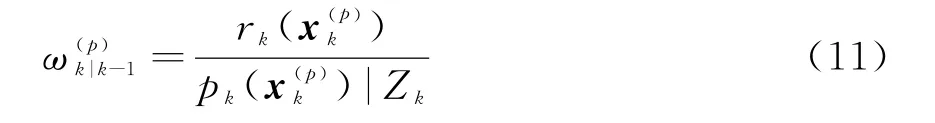
狀態更新：

對于k時刻粒子p=1,…,L k-1+J k的更新權重可由下式計算：

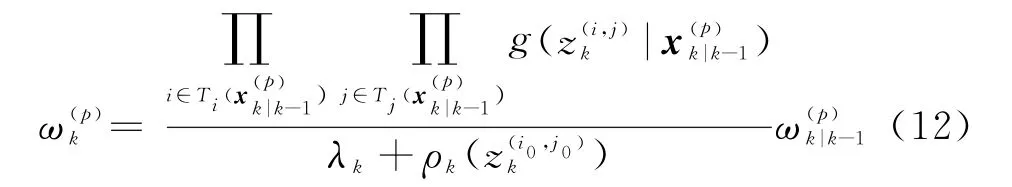
式中,λk為雜波分布的歸一化常數,通常設為1,

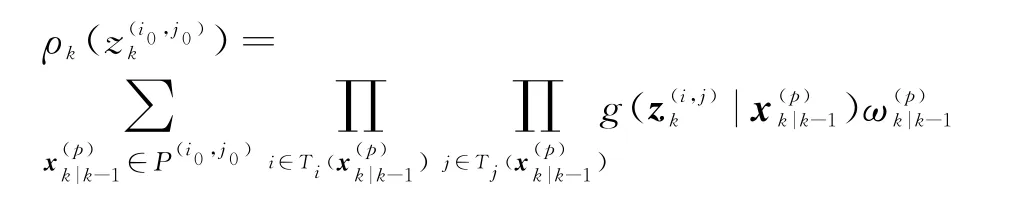
任一分辨單元(i0,j0)內粒子集合為

3 RBPF-PHD-TBD算法

將RBPF濾波與PF-PHD-TBD方法相結合,其主要思想是在粒子的預測和更新過程中,用RBPF取代基本粒子濾波,充分利用線性狀態與非線性狀態的關聯特性,提高權重計算的準確度。其詳細計算步驟如下：

步驟1 狀態預測

對于k時刻“存活”粒子,先將其狀態向量進行分割,,和分別表示向量x k在k時刻的線性和非線性部分,則粒子的狀態方程和測量方程改寫如下：

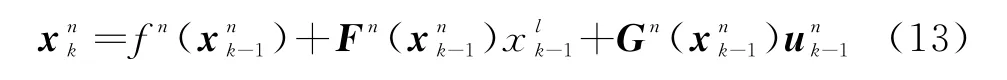
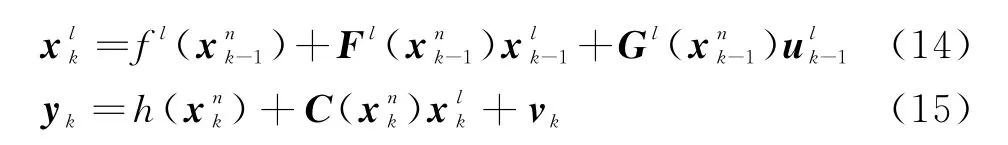
式中,;v k～N(0,R k)。

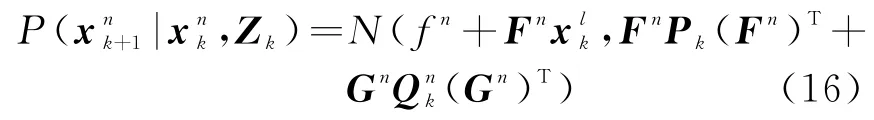
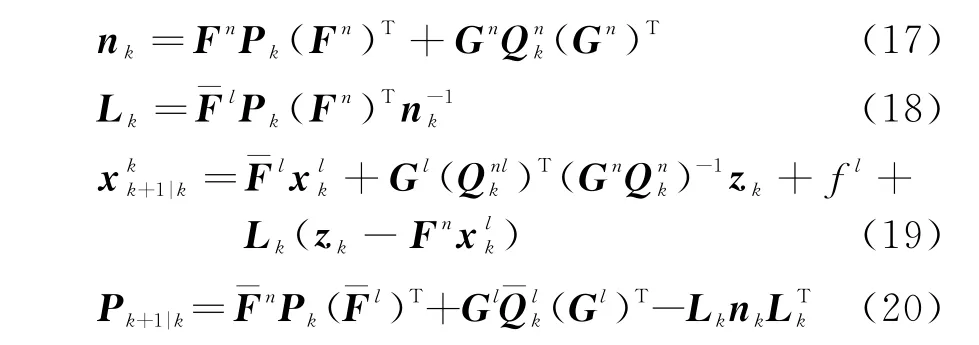
對所有的k時刻“存活”粒子,根據式(9)計算粒子的權重。

對于k時刻“新生”粒子,根據“新生”粒子初始化方法求取其狀態分布和協方差,即

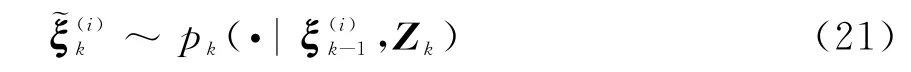
步驟2 狀態更新

對于k+1時刻所有的“存活”粒子和“新生”粒子,根據式(12)計算粒子的權重,經過重采樣之后提取權重較大的粒子的非線性狀態作為更新后粒子的非線性狀態;然后,對粒子線性部分的均值和協方差作卡爾曼濾波更新：

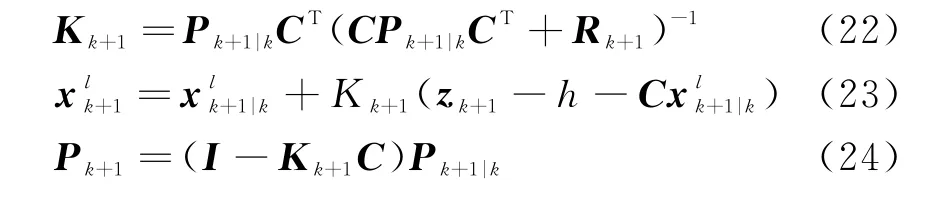
4 仿真驗證

假設在雷達的觀察區域內存在4個目標,各個目標在不同的時刻出現和消失,即目標數是時變的;4個目標的幅度是固定的,且都設為20;背景噪聲方差根據目標功率和信噪比產生,信噪比計算公式為SNR=10 lg(P/2σ2),且SNR=9 dB;仿真時間為40幀,當前目標在下一時刻的存活概率為e k|k-1=0.95;不考慮目標分裂的情況,每一幀新生目標數目服從均值0.2的泊松過程;設定初始存活粒子數L k=2 000,每一幀新生粒子采樣數J k=2 000,初始存活粒子與新生粒子均服從觀測區域上的平均分布。觀察區域大小為40 km×60 km。具體場景設置如表1所示。

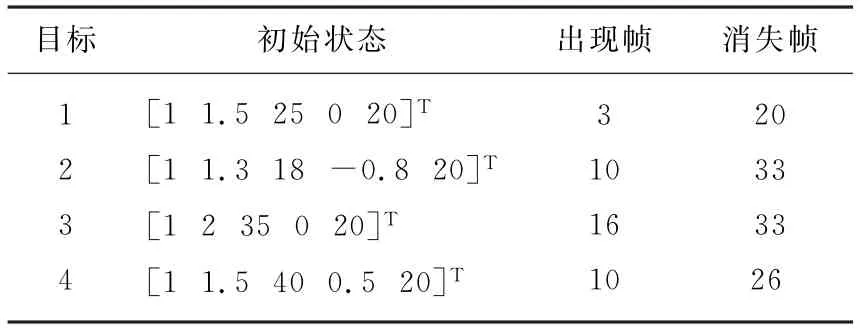
表1 目標運動狀態設定

目標滿足近似勻速運動模型,

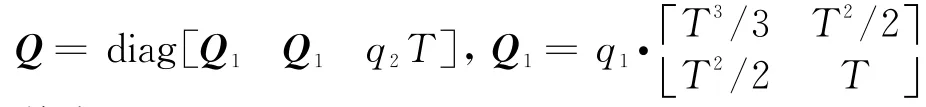
根據RBPF濾波思想可以將目標狀態改寫為X k=[x n,x l]T,其中x n=[x y I]表示與量測有關 的 目 標 位 置 與 強 度 信 息,表 示 獨 立于量測的目標速度信息。改寫后的動態方程為

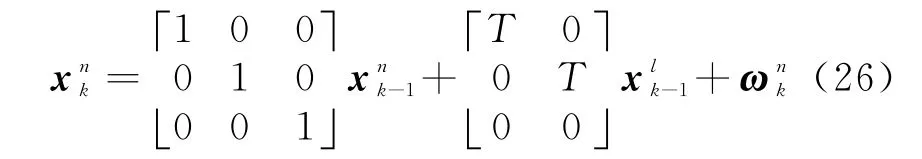
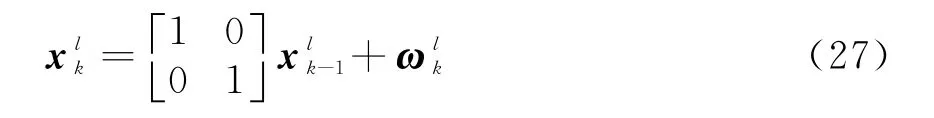
通過將目標的狀態方程和量測方程與式(13)～(15)比較可以得到各個狀態轉移矩陣如式(28)所示;將式(28)中各公式代入式(16)～(24)可對RBPF-PHD-TBD的算法步驟進行簡化。

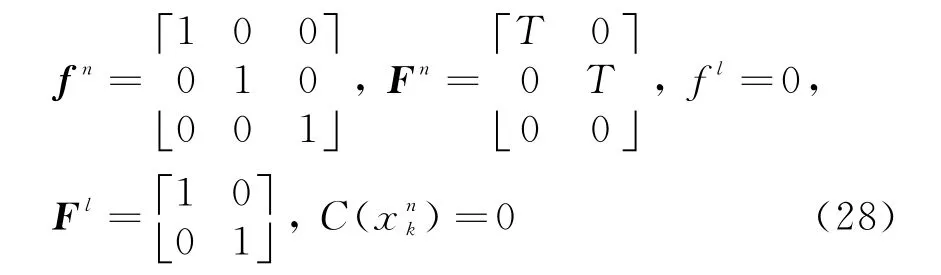
對于單目標檢測前跟蹤,其評價指標通常為最小均方誤差;對于多目標檢測前跟蹤,其評價指標不容易定義,這是因為算法在估計每一個目標狀態的同時還要估計目標的數目(集合的勢),而真實目標狀態的集合和估計得到的目標狀態集合的勢并不一定相等。目前評估多目標跟蹤性能的方法有很多,比如最優子模式指派距離,Hausdorff距離和 Wasserstein距離等。 本文中采用Wasserstein距離,其定義為任意兩個非空子集^X,X上,

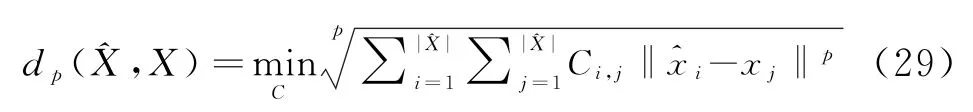
仿真結果如圖1～圖5及表2所示。

圖1為兩種算法分別對目標進行跟蹤得到的粒子云狀態。其中,深色的表示PF-PHD-TBD,淺色的表示RBPF-PHD-TBD。可以看到,兩種算法都能較好地檢測并跟蹤到目標,但是PF-PHD-TBD出現了許多錯誤的粒子云,將會輸出錯誤點跡,而RBPFPHD-TBD的粒子云與目標位置完全相符,不會輸出錯誤點跡;并且,就粒子云的體積來看,RBPFPHD-TBD明顯小于PF-PHD-TBD,即粒子分布更加集中,這是由于其狀態估計的協方差更小。圖2為對粒子提取狀態后分解到兩個坐標軸之后的跟蹤點跡,深色的表示PF-PHD-TBD,淺色的表示RBPF-PHD-TBD。可以看到,與圖1所示本質上一致,即兩種算法都能跟蹤上目標,但是PF-PHD-TBD會輸出許多錯誤點跡,從而造成虛警。

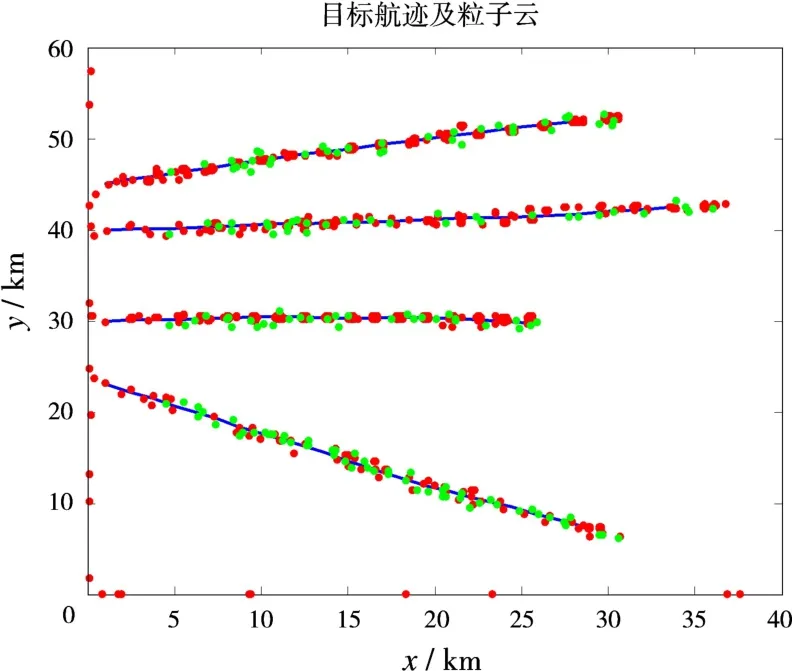
圖1 目標跟蹤的粒子云

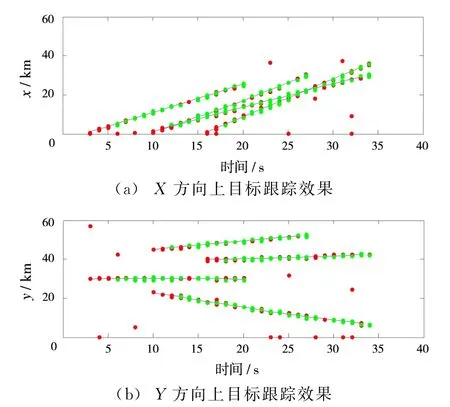
圖2 分解后目標跟蹤效果

圖3為10次仿真后兩種算法估計的目標數目平均值,從總體上看,RBPF-PHD-TBD的估計更加準確,與目標真實數目更加接近,這是由于其充分利用了各維狀態信息,通過狀態之間的關聯實現粒子權重的更準確計算。

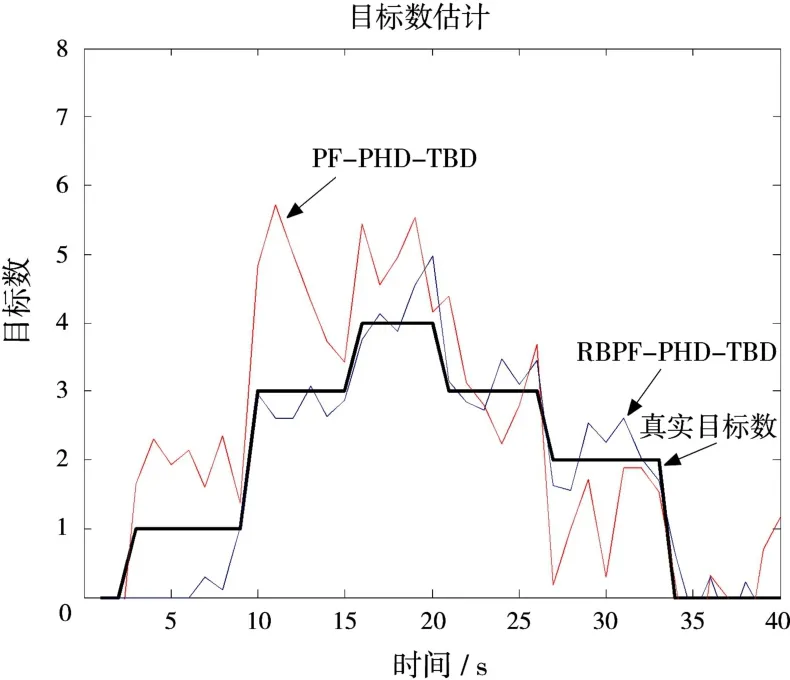
圖3 目標數估計

從上述3張圖中還可以看到,PF-PHD-TBD對目標數目的變化非常靈敏,一是能夠在接近目標出現的時刻作出數目估計,并跟蹤上目標;二是在有目標消失的時刻也響應迅速,但是卻存在目標估計數變化劇烈、估計不準確的問題。相比之下,RBPF-PHD-TBD在開始時刻則有幾幀延遲,需要多幀積累之后才作出響應,在其他時刻,對目標數目變化的響應也比較穩健,因此當有目標出現或消失時變化并不像PF-PHD-TBD一樣劇烈。

圖4為10次仿真中脫靶距離比較,可以看到在目標存在的大部分時刻,RBPF-PHD-TBD的跟蹤誤差都明顯小于PF-PHD-TBD。

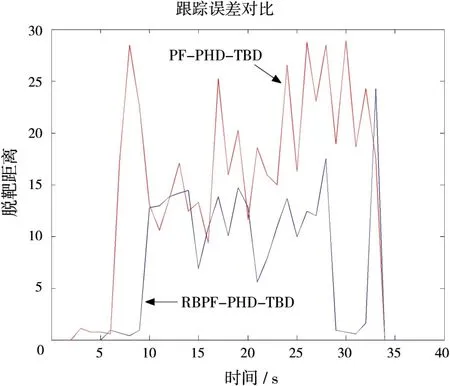
圖4 Wasserstein距離

對兩種算法的運行時間進行統計,求出10次實驗中的運行時間并取平均值。所用電腦配置為：處理器,Core i5-4570 3.20GHz;操作系統,Win7旗艦版64位(Direct X 11);內存,8 GB(DDR3 1 600 MHz)。

表2為10次實驗的平均運行時間,可以求出RBPF-PHD-TBD的運行時間大致為PF-PHDTBD的37.8%。圖5為每一次實驗的運行時間,其中橫軸上序號11表示的是10次實驗的平均運行時間。從表2與圖5可以看到,采用RBPF濾波顯著降低了算法的計算負擔,提高了實時性。

表2 兩種算法平均運行時間

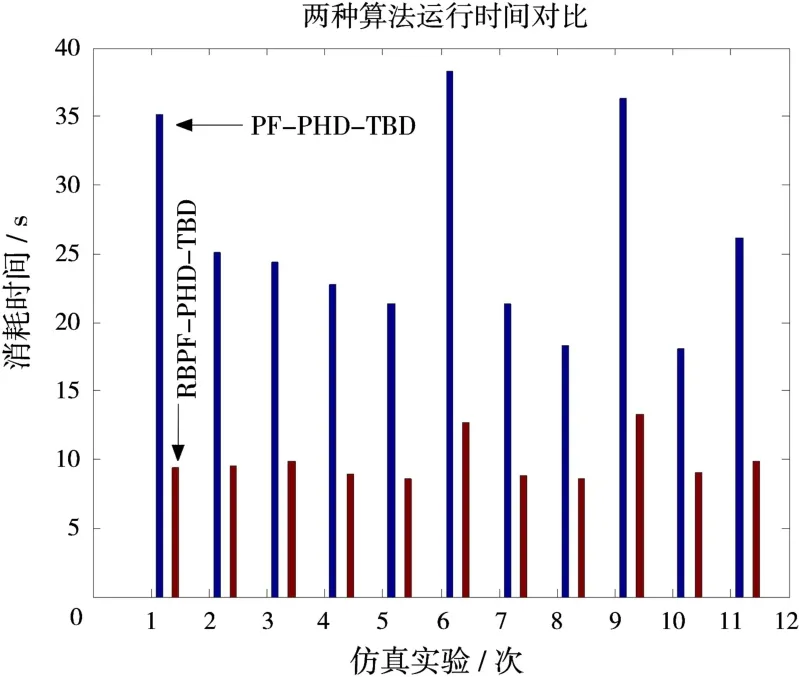
圖5 兩種算法運行時間

5 結束語

本文提出了一種采用Rao-Blackwellised粒子濾波的PHD多目標檢測前跟蹤改進方法。該方法將目標的多維狀態空間進行分解,分別用線性和非線性濾波器進行跟蹤,降低了傳統PF-PHD-TBD的運算復雜度,使其運算時間降低為原來的大約37.8%;同時,由于充分利用了各維狀態信息及狀態關聯特性,其對目標數目的估計更加準確,狀態估計方差更小,粒子云更加集中,跟蹤精度更高。

[1]王云奇,孔令講,易偉,等.一種耦合檢測和JPDA濾波的多目標跟蹤算法[J].雷達科學與技術,2014,12(2)：143-148.

WANG Yuqi,KONG Lingjiang,YI Wei,et al.Integration of Detection with JPDAF for Multi-Target Tracking[J].Radar Science and Technology,2014,12(2)：143-148.(in Chinese)

[2]尹帥,袁俊泉,吳順華,等.一種改進的JIPDA多目標跟蹤算法[J].雷達科學與技術,2014,12(3)：285--290.

YIN Shuai,YUAN Junquan,WU Shunhua,et al.An Improved JIPOA Algorithm for Multi-Target Tracking[J].Radar Science and Technology,2014,12(3)：285-290.(in Chinese)

[3]BOERS Y,DRIESSEN J N.Multitarget Particle Filter Track-Before-Detect Application[J].IEE Proceedings Radar,Sonar and Navigation,2004,151(6)：351-357.

[4]MAHLER R.Multitarget Bayes Filtering via First-Order Multitarget Moments[J].IEEE Trans on Aerospace and Electronics Systems,2003,39(4)：1152-1178.

[5]VO B N,SINGH S,DOUCET A.Sequential Monte Carlo Methods for Multitarget Filtering with Random Finite Sets[J].IEEE Trans on Aerospace and Electronics Systems,2005,41(4)：1224-1245.

[6]VO B N,MA W K.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Trans on Signal Processing,2006,54(11)：4091-4104.

[7]PUNITHAKUMAR K,KIRUBARAJAN T,SINHA A.A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-Before-Detect[C]∥17th Conference on Signal and Data Processing of Small Targets,San Diego,CA：SPIE,2005：1-8.

[8]HABTEMARIAM B K,THARMARASA R,KIRUBARAJAN T.PHD Filter Based Track-Before-Detect for MIMO Radars[J].Signal Processing,2012,92(3)：667-678.

[9]林再平,周一宇,安瑋.改進的概率假設密度濾波多目標檢測前跟蹤算法[J].紅外與毫米波學報,2012,31(5)：475-480.

[10]占榮輝,劉盛啟,歐建平,等.基于序貫蒙特卡羅概率假設密度濾波的多目標檢測前跟蹤改進算法[J].電子與信息學報,2014,36(11)：2593-2599.

[11]林再平,周一宇,安瑋,等.基于概率假設密度濾波平滑器的檢測前跟蹤算法[J].光學學報,2012,32(10)：1-8.

[12]LEHMANN F.Recursive Bayesian Filtering for Multitarget Track-Before-Detect in Passive Radars[J].IEEE Trans on Aerospace and Electronics Systems,2012,48(3)：2458-2480.

[13]胡振濤,付春玲,劉先省.基于RB粒子濾波的多傳感器目標跟蹤融合算法[J].光電子·激光,2012,23(3)：566-571.

[14]GONZALEZ-DUARTE S,CHACON-MURGUIA M I.Rao-Blackwellized Particle Filter for Multiple Object Tracking in Video Analysis[C]∥11th International Conference on Electrical Engineering,Computing Science and Automatic Control,Campeche：IEEE,2014：978-985.

[15]趙增順,林艷艷,馮翔,等.基于高斯粒子群優化的RBPF濾波算法[J].計算機應用研究,2015,32(2)：423-426.

[16]VIHOLA M.Rao-Blackwellised Particle Filtering in Random Set Multitarget Tracking[J].IEEE Trans on Aerospace and Electronics Systems,2007,43(2)：689-705.

[17]莊澤森,張建秋,尹建君.Rao-Blackwellised粒子概率假設密度濾波算法[J].航空學報,2009,30(4)：698-705.