半潛船裝載特定貨物前初穩(wěn)性高度可行域探討*

汪　洋　謝新連　李曉君

(大連海事大學(xué)綜合運輸研究所　大連　116026)

半潛船裝載特定貨物前初穩(wěn)性高度可行域探討*

汪洋謝新連李曉君

(大連海事大學(xué)綜合運輸研究所大連116026)

摘要：對于載運重大件的半潛船，多數(shù)權(quán)威機構(gòu)只規(guī)定了初穩(wěn)性高(GM)的最小限值，但未對GM最高限值做出規(guī)定.GM過大時，船舶橫搖周期就會變短，船舶在風(fēng)浪中會產(chǎn)生劇烈搖蕩.為保障運輸安全，從提供足夠的復(fù)原力及避免諧搖這兩個角度出發(fā)，推導(dǎo)出半潛船穩(wěn)性高可行域計算公式.在裝載某一特定重大件前，利用該公式初步判斷半潛船裝載該重大件時初穩(wěn)性高是否滿足要求.以一艘半潛船運載自升式鉆井平臺為例，利用該計算公式對其穩(wěn)性進行了分析，同時根據(jù)該公式提出提高船舶航行穩(wěn)性的方法.

關(guān)鍵詞：半潛船；初穩(wěn)性高度；最低復(fù)原力；諧搖

汪洋 (1991- ):男，碩士生，主要研究領(lǐng)域為綜合運輸

0引言

近年來隨著對海洋能源的開發(fā)和利用不斷增加，油氣生產(chǎn)設(shè)備、鉆井平臺等大型裝備的整體運輸需求快速增長，為適應(yīng)海洋資源的開發(fā)利用，迫切需要安全可靠的重大件運輸工具，半潛船應(yīng)需而生[1].由于鉆井平臺等油氣生產(chǎn)裝備的質(zhì)量和尺寸都很大，對半潛船的穩(wěn)性提出了較高要求.

初穩(wěn)性高GM是衡量船舶穩(wěn)性的一個重要指標(biāo)[2].GM值過低，船舶在受到風(fēng)浪作用橫傾時難以提供足夠的復(fù)原力回復(fù)到平衡狀態(tài)[3].GM值過大，船舶的橫搖周期就會變短，在風(fēng)浪中會產(chǎn)生劇烈搖蕩，對船舶的安全性同樣有不利影響[4].然而，國際上很多權(quán)威機構(gòu)只對半潛船的GM最低限值作出了要求，卻沒有規(guī)定GM的上限.因此，確定半潛船GM的合理取值范圍值得研究.

貨物裝上船后，船舶的穩(wěn)性變化是復(fù)雜的，且對于不同的貨物，船舶穩(wěn)性也不同.本文試圖從滿足最低復(fù)原力及避免諧搖2個方面，推導(dǎo)出船舶裝載某一特定貨物后為保證穩(wěn)定航行所要求的船舶空載穩(wěn)性高度的取值范圍.通過與實船空載穩(wěn)性高度做簡單對比，即可對船貨組合體穩(wěn)性作出預(yù)判斷.

1半潛船初穩(wěn)性高度限定標(biāo)準(zhǔn)

國際上有很多機構(gòu)對半潛船的穩(wěn)性高度做出了要求.如國際海事組織(IMO)在RESOLUTION A.749(18)決議中要求GM不小于0.15 m[5]，中國船級社《半潛船檢驗指南》[6]、中國海事局《船舶與海上設(shè)施法定檢驗規(guī)則》[7]、GL Noble Denton公司“Guidelines for Marine Transportations”[8]都指出半潛船GM不應(yīng)小于 1.0 m.雖然各機構(gòu)對半潛船GM的最低值的規(guī)定存在一定差異，但是，值得一提的是，所有的機構(gòu)只對船舶GM最低值做出要求，并沒有對其設(shè)置上限.

當(dāng)船舶與波浪發(fā)生諧搖時，船舶的橫搖幅度很大，容易發(fā)生險情，船舶在航行過程中應(yīng)避免與波浪的諧搖.船舶諧搖取決于船舶橫搖固有周期與波浪周期之比，而橫搖固有周期由船寬、GM等因素決定.因此，通過以上關(guān)系可推導(dǎo)出GM的最高限值.

2初穩(wěn)性高度限值計算

2.1滿足最低復(fù)原力要求

船舶受到風(fēng)浪等因素作用時，發(fā)生橫傾，重力作用點和浮力作用點不在同一鉛垂線上，會產(chǎn)生一個復(fù)原力矩.船舶的完整穩(wěn)性將取決于該復(fù)原力矩與擾動力矩的相對大小[9].而復(fù)原能力的強弱與初穩(wěn)性高度GM的大小呈正相關(guān)[10].因此，該復(fù)原力矩能否使船舶恢復(fù)到平衡狀態(tài)與船舶初穩(wěn)性高GM相關(guān).為了保證船舶橫傾時有足夠的復(fù)原力，GM應(yīng)滿足一個最低限值.

本文采用中國船級社及GL Noble Denton公司等機構(gòu)的規(guī)定，要求半潛船的初穩(wěn)性高GM在任何情況下不得小于1.0 m，即：

GM≥1

(1)

令GMe為船舶空載時的初穩(wěn)性高度.當(dāng)半潛船載貨航行時，船貨組合體的GM值變?yōu)?/p>

GM=GMe+ΔGM

(2)

(3)

式中：ΔGM為裝貨后穩(wěn)性高度改變量；P為貨物重量；d為裝卸前吃水；zp為貨物重心距船舶基線高；e為裝貨后船舶排水體積改變量的浮心與裝貨前WL水線的距離.

基于半潛船的船體形狀特點，可以取：

(4)

式中：Δdp為吃水改變量.

在半潛船中，吃水改變量Δdp可近似等于：

(5)

(6)

式中：ρ為海水密度；Aw為水線面面積；L為船長；B為船寬.

由式(1)～(6)可得：

(7)

對于某一特定貨物，只有船舶GMe滿足式(7)計算的最低限值時，才能使船貨組合體的穩(wěn)性高度滿足最低復(fù)原能力的要求.

2.2避免諧搖

船舶在波浪中橫搖幅值的大小，與波浪擾動力的大小相關(guān)，也與橫搖調(diào)諧因數(shù)相關(guān).令Λφ表示橫搖調(diào)諧因數(shù)，它等于船舶橫搖固有周期與波浪周期之比，即[11]

(8)

式中：Tφ為船舶橫搖固有周期；T為波浪周期.

當(dāng)Λφ=1，即船舶橫搖固有周期等于波浪周期時稱為諧搖.此時，波浪對船做的功最多，船舶的橫搖幅度很大，穩(wěn)性最差.當(dāng)0.7<Λφ<1.3時，船舶處于諧搖區(qū)，船舶的穩(wěn)性仍會受到很大影響.因此，為保證安全航行，Λφ需滿足：Λφ≤0.7或Λφ≥1.3.

當(dāng)Λφ≤0.7時，船舶不處于諧搖區(qū)，但船舶的固有橫搖周期Tφ相對于波浪周期T較小，船舶的橫搖固有頻率較快，船體遇到風(fēng)浪后會產(chǎn)生急劇的搖擺.因此，當(dāng)Λφ≤0.7時，雖然船舶可以避免與波浪的諧搖，但這是以加快船舶橫搖頻率為代價的，對船舶的穩(wěn)性同樣有不利影響.在船舶航行中，也應(yīng)該盡量避免Λφ≤0.7這種情況.

當(dāng)Λφ≥1.3時，船舶的橫搖固有周期Tφ相對于波浪周期T較大.此時，船舶橫搖頻率較慢，在有效地避免諧搖區(qū)的同時，能夠保證船舶平穩(wěn)航行.綜合考慮，Λφ應(yīng)滿足：

(9)

船舶橫搖固有周期Tφ是表征橫搖的一個重要參數(shù)，對于狀態(tài)確定的船舶來說，Tφ是一個固定數(shù)值.Tφ的計算如下[12]

(10)

式中：k為系數(shù)，一般取0.4.

在深水中，波浪的波長、周期及波速之間的關(guān)系為

(11)

(12)

式中：T為波浪周期；λ為波浪波長；cw為波速.

然而，當(dāng)船舶以一定的速度和航向航行時，船體感受到的波速已經(jīng)不是波浪的實際速度，作用在船體上的波浪周期也已經(jīng)發(fā)生了變化，波浪的周期已經(jīng)不是自然周期T，而是遭遇周期Te.船舶在海上航行時，其航行方向與波浪去向的夾角稱為遭遇浪向角β.β如圖1所示，當(dāng)船舶順浪航行時，β為0o；橫浪時，β為90o；頂浪時，β為180°.

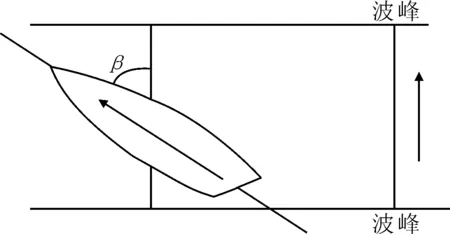
圖1　船舶遭遇浪向角β

假設(shè)船舶在規(guī)則波中以船速V,遭遇浪向角β航行時，波浪的遭遇周期Te為

(13)

由式(9)～(13)可得：

(14)

由式(2)～(6)及式(14)可得，為了使船舶避免諧搖，船舶空載時的初穩(wěn)性高度GMe應(yīng)滿足

(15)

綜合式(7)和式(15)，得

(16)

對于一個特定的重大件貨物，在裝貨前，可以利用式(16)對船貨組合體的穩(wěn)性進行簡要的判斷.將貨物的相關(guān)參數(shù)、船舶相關(guān)參數(shù)及航線所經(jīng)海域的相關(guān)參數(shù)代入式(16)計算得出船舶裝載該貨物時GMe所需滿足的取值范圍.若GMe滿足式(16)計算得出的取值范圍，那么，就可以認(rèn)為該半潛船裝載這個重大件后，具有足夠的穩(wěn)性.

當(dāng)知道船舶吃水與排水量的關(guān)系時，上式還可以用于計算半潛船下潛過程中的穩(wěn)性要求.

3算例驗證與分析

3.1算例

某半潛船，運載一件自升式鉆井平臺.該半潛船的相關(guān)參數(shù)如下：船長L為207.93 m；型寬B為44.5 m；最大航速為14 kn；船舶未載貨時GMe為15.64 m,吃水d為7.1 m，重量D為51 713.41 t.

該自升式鉆井平臺的相關(guān)參數(shù)如下：重量P為13 931.13 t；裝上船后重心高度zp為42.259 m.

航線為天津到新加坡.假設(shè)船舶以最大航速14節(jié)航行，遭遇浪向角β為60°，已知太平洋的平均波長為73 m.

根據(jù)式(16)計算，要使船舶裝載該自升式鉆井平臺后具有足夠的穩(wěn)性，船舶GMe應(yīng)在[10.54,18.35 m]這個區(qū)間內(nèi)，而此半潛船的GMe為15.64 m，屬于這個區(qū)間.因此，該半潛船裝載該自升式鉆井平臺后穩(wěn)性較好.

3.2分析

圖2～4分別為改變船速、遭遇浪向角以及貨物重心高度后，GMe取值范圍的變化情況.

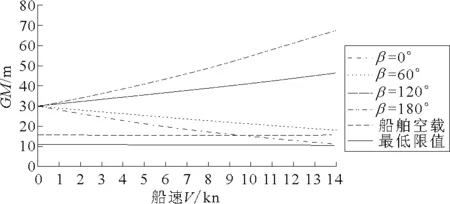
圖2　β分別為0°,60°,120°,180°，GM取值范圍隨V的變化

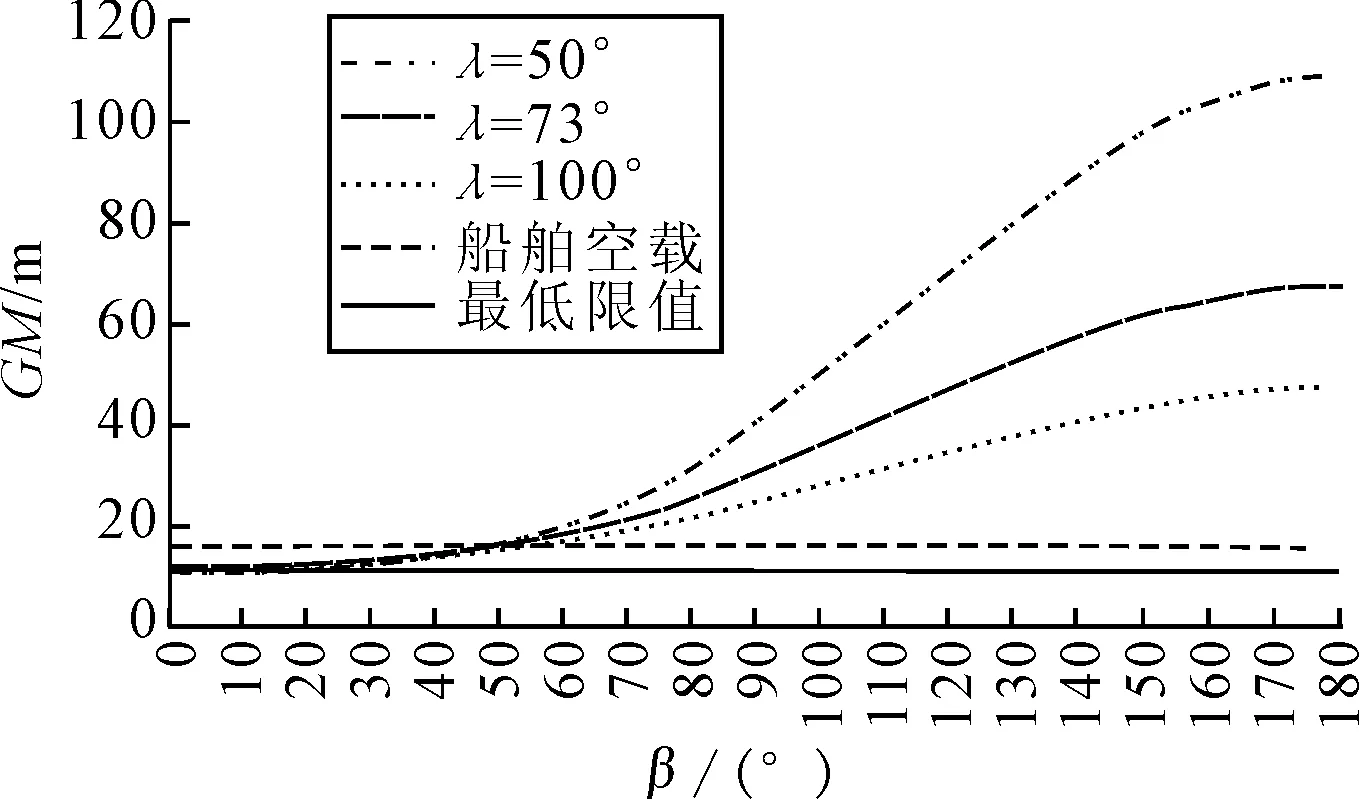
圖3　λ分別為50,73,100 m時，GM取值范圍隨β的變化

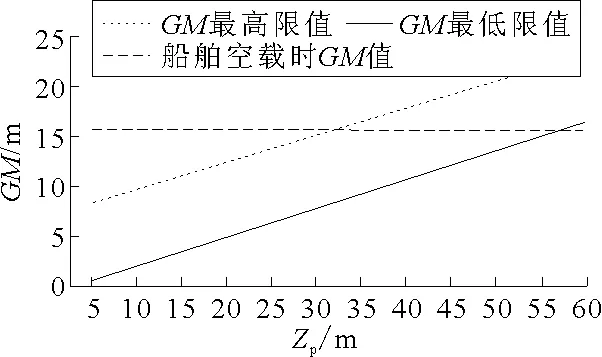
圖4　貨物重量不變，GM取值范圍隨貨物重心的變化

以圖2中的β=60o的曲線為例.令β=60°的曲線與GM最低限值曲線圍成的范圍為S,那么，對于GMe這條曲線上的所有點來說，在范圍S內(nèi)的點即滿足穩(wěn)性要求，而在范圍S外的點，不滿足穩(wěn)性要求.由圖2可知，β=60°,120°,180°時，無論船速為多少，GMe上的點都在相應(yīng)的S內(nèi)，即在這種狀況下無論船速為多少，船舶都滿足穩(wěn)性高的要求.而對于β=0°來說，只有當(dāng)航速小于等于9.24 kn時，船舶才滿足穩(wěn)性要求.

4結(jié)束語

本文提出了一個通用判別式，判別式能對半潛船裝載貨物后是否滿足穩(wěn)性要求進行簡要的判斷.對于一個特定的貨物，船舶以一定的速度、遭遇浪向角航行時，可以計算出為平穩(wěn)載運該貨物船舶空載GMe所需滿足的范圍.如果實船的GMe值在該范圍內(nèi)，則該船舶裝載這個貨物航行時，船貨組合體既可以滿足最低復(fù)原力的限定，也可以有效地避免與波浪的諧搖，船舶的穩(wěn)性可以滿足安全航行的要求.

若船舶裝載貨物后，船舶平穩(wěn)航行所要求的GM取值范圍不包括GMe,即船貨組合體不滿足穩(wěn)性要求，則可以通過改變以下條件來改變船舶的穩(wěn)性狀態(tài)：(1)調(diào)整航速；(2)改變船舶遭遇浪向角；(3)通過合理壓載調(diào)整船貨組合體的重心高度.

參 考 文 獻

[1]鐘毓凌,閔娟娟.半潛船操作仿真軟件的設(shè)計[J].中國水運,2009(9):86-87.

[2]胡麗芬,馬坤,紀(jì)卓尚,等. 破損艦船最小初穩(wěn)性高計算方法研究[J]. 武漢理工大學(xué)學(xué)報:交通科學(xué)與工程版,2012,36(6):1225-1227.

[3]張平,何斌.改善船舶完整穩(wěn)性的措施[J].江蘇船舶,2001(2):8-11.

[4]VOOTG A J,SOLES J J,DIJK R.Mean and low frequeney roll for semi-submersibles in wavcs[C].ISOPE Conff,2002:1-6.

[5]國際海事組織. 完整穩(wěn)性規(guī)則2008 [S].北京:人民交通出版社,2008.

[6]中國船級社. 半潛船檢驗指南(評審稿) [EB/OL].http://www.eworldship.com/uploadfile/2012/0904/20120904103904467.pdf, 2006.

[7]中華人民共和國海事局. 船舶與海上設(shè)施法定檢驗規(guī)則:2011 [S]. 北京: 人民交通出版社,2011.

[8]GL Noble Denton.Guidelines for marine transportations [EB/OL].http://www.dnv.com/industry/oil_gas/rules_standards/noble_denton_rules_guidelines.asp, 2010.

[9]TAYLAN M.Overall stability performance of alternative hull forms [J].Ocean engineering, 2002, 29(13):1663-1681.

[10]杜嘉立,姜華.船舶原理[M].大連：大連海事大學(xué)出版社, 2011.

[11]盛振邦,劉應(yīng)中.船舶原理[M].上海：上海交通大學(xué)出版社, 2003.

[12]黃志.雜貨船初穩(wěn)性測定及其誤差分析[J].集美航海學(xué)院學(xué)報，1996(1)：23-26.

中圖法分類號：U661.2

doi:10.3963/j.issn.2095-3844.2015.01.026

收稿日期：2014-05-27

Stability Judgment of the Semi-Submersible Vessel Before Laden

WANG YangXIE XinlianLI Xiaojun

(IntegratedTransportInstitute,DalianMaritimeUniversity,Dalian116026,China)

Abstract：For semi-submersible vessels carrying special heavy cargo, most authorities only provides a minimum limit of GM, without a provision for the maximum limit of GM. However, when GM is too high, the rolling period of the vessel will become shorter, which will cause severe shaking. From the aspects of providing sufficient righting arm and avoiding harmonic shake, this paper deduces a formula to calculate the feasible range of GM to maintain the stability of the semi-submersible vessel. Before the semi-submersible vessel loading a specific special heavy cargo, this formula can be used to preliminary judge whether the GM of this vessel meeting the requirement to load this cargo. Finally, a semi-submersible vessel carrying a jack up drilling platform is taken an example, by using this calculation formula, the stability of the semi-submersible vessel is analyzed and some methods improving sailing stability have been put forward.

Key words：semi-submersible vessel；metacentric height；righting arm；harmonic shake

*國家自然科學(xué)基金資助項目 (批準(zhǔn)號：50778029)