測點級聲學故障檢測中的報警頻次建模方法研究

任安民　 何　琳　程　果

(海軍工程大學振動噪聲研究所1)　船舶振動噪聲重點實驗室2)　武漢　430033)

測點級聲學故障檢測中的報警頻次建模方法研究

任安民1，2)何琳1，2)程果1，2)

(海軍工程大學振動噪聲研究所1)船舶振動噪聲重點實驗室2)武漢430033)

摘要：文中圍繞測點級聲學故障檢測方法開展研究，根據區間估計原理建立頻帶能量超標檢測流程，針對隨機報警事件干擾提出基于報警事件頻次建模的二級閾值檢測法，并利用實測數據進行了算法驗證.數據分析顯示，該方法能夠有效檢測正常工況下的隨機報警事件干擾，降低測點級聲學故障檢測的虛警率.

關鍵詞：聲學故障；頻帶能量；隨機報警事件；泊松分布；二級閾值

任安民(1980- )：男，博士生，助理研究員，主要研究領域為船舶振動與噪聲控制技術

0引言

潛艇聲學故障(acoustic fualt，AF)是指潛艇服役期間因設備故障或老化、隔振安裝失效、維修改裝等技術狀態變化，以及航行期間的武器發射、舵機運行、人員活動等瞬態偶發事件，導致的設計隱身指標受損、可探測性惡化，威脅潛艇隱蔽航行及任務執行的異常現象[1].實現潛艇聲學故障的檢測及修復，是維護潛艇聲隱身性、實現動態聲學特征管理的先決條件，正逐步受到各方關注.

根據故障信號特征不同，潛艇聲學故障可分為穩態聲學故障和瞬態聲學故障2大類；典型的聲學故障包括頻帶能量超標、“線譜事件”等，如總聲(振)級超標、1/3 oct頻帶級超標,以及線譜新增、線譜增強、線譜遷移等[2-4].根據故障檢測部位及危害程度不同，聲學故障又可進一步分為測點級、區域級和全艇級3類；測點級聲學故障定位于根據艇體單測點數據檢測發現振動噪聲異常，能夠及時、客觀描述測點所在部位聲學狀態，在實艇聲學狀態評估中應用廣泛.美軍自20世紀80年代起就關注艇載設備振動噪聲異常的檢測問題，最初以正常工況特征頻段振級加6 dB作為檢測基準，高出基準6～8 dB認為出現異常[5]；“全艇監控系統(TSMS)”裝艇應用后聲學故障概念進一步明確，主要依賴艇體結構振動及自噪聲測點進行故障檢測[6].近年來國內有關單位也相繼開展相關研究，但主要以設備振動狀態監測為主，缺乏針對艇體結構振動信息的檢測算法分析.

本文基于統計分析理論對測點級聲學故障在線檢測方法進行研究，圍繞測點級聲學故障檢測流程、虛警率控制等問題進行深入分析.在實現頻帶能量超標檢測的基礎上，針對實艇復雜干擾導致的隨機報警事件進行建模及二級閾值設計，實現對故障檢測虛警率的有效控制，為聲學故障修復提供有效決策信息.

1測點級聲學故障檢測基本流程

根據工程經驗及實測數據分析，艇體結構振動測點的頻帶能量總級服從或近似服從獨立正態分布，在2 000 Hz以下中低頻段檢驗特征量尤其符合檢驗條件.在此基礎上，根據區間估計原理可對測點總級進行假設檢驗，進而將給定置信水平下的總級超標事件檢測流程設計如下.

1.1確定采樣序列樣本容量

針對給定工況的艇體結構振動及自噪聲狀態進行數據采集，樣本容量N由下式確定

(1)

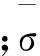
(2)

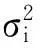
1.2計算總級及相關統計量

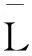
(3)

(4)

(5)

1.3離群值的剔除及檢驗

為滿足正態分布要求，計算總級閾值前應進行必要的離群值檢測與剔除，步驟如下.

(6)

(7)

步驟2.確定檢出水平α，在“Grubbs檢驗法臨界值表”中查出對應N與α/2的臨界值G1-α/2(N).

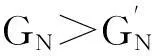
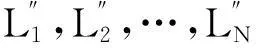
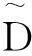
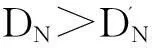
1.4建立基準閾值

將經過上述處理得到的總級序列重新記為L1，L2，…，LN，若以μ和σ分別表示樣本期望和標準差，則總級序列的概率密度函數f(L)可寫成

(8)

基于正態分布的區間估計原理，總級樣本落入區間(μ-2σ,μ+2σ)的概率約為95.5%，落入區間(μ-3σ,μ+3σ)的概率約為99.7%.據此認為總級實測值大于μ+2σ為小概率事件，以此作為測點級聲學故障檢測預警閾值，而將μ+3σ設為報警閾值.

2基于報警頻次建模二級閾值設計

實艇檢測過程中，由于海洋環境、人員活動等復雜因素干擾，檢測結果容易出現大量誤報警信息，給艇員正常操作及響應造成負擔，因而有必要對檢測結果進行分類識別、增強報警信息的針對性.在此使用“隨機報警事件(arbitrary alarm event，AAE)”對上述干擾做統一描述，考慮此類事件持續時間短、隨機性強、能量分布不規律，本文提出考察其單位時間報警頻次進行二級檢測閾值(double stages threshold，DST)設計，進而實現報警信息分類檢測.其本質上是參照時頻分析思想，在單時刻總級估值問題中引入報警事件的連續時間分布，實現報警事件的二次檢測.

2.1隨機報警事件的概率分布

測點級聲學故障檢測結果符合典型的“0-1分布”，或者1(超標)、或者0(未超標).假定給定工況下艇體振動處于穩定狀態，測點總級符合正態分布，則在此期間偶爾出現的隨機報警事件為小概率事件，且滿足以下條件.

1) 報警事件之間相互獨立，即在時刻t出現的總級超標事件在t+Δt時刻不一定重復出現.

2) 如果時間間隔Δt足夠小，那么Δt內發生隨機報警事件的概率與Δt近似成正比，即概率非線性度為Δt的高階無窮小.

3) 如果時間間隔Δt足夠小，那么Δt內發生兩次或多次隨機報警事件的概率是發生一次報警事件概率的高階無窮小.

4) 零時刻不會出現超標事件.

在此基礎上，根據泊松定理(二項分布的泊松逼近)及泊松分布概率密度函數，可以得到t1～t2時段內發生k次隨機報警事件的概率P(t1,t2).

(9)

式中：k為t1～t2時段隨機報警事件次數；λ為與t1～t2對應的大于0的常數，由報警事件頻次信息統計分析確定.

2.2參數選擇及二級閾值設定

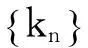
(10)

將λ代入式(9)，可得到時段Δt=t2-t1內發生k次隨機超標事件的概率.在此基礎上，根據測點級聲學故障檢測的檢測率、虛警率等指標要求，可對應建立針對隨機報警次數的二級閾值k0.假定給定工況下Δt內發生k0次以上報警事件，則基于一定置信水平認為發生聲學故障；若報警頻次低于k0則判定狀態正常.顯然，二級閾值k0取決于參數λ和檢驗置信水平，λ可通過報警頻次樣本統計獲取，置信水平需根據故障檢測要求設定，通常取95%以上.

3數據分析

3.1一級檢測閾值檢驗

為檢驗上述方法的有效性，本文利用實船航行測噪所獲數據進行算法驗證.首先選取主軸轉速22 r/min時殼體測點FJ01,FJ13分別建立總級序列，樣本時長1s、數量100組；其次，根據上述檢測流程計算檢測閾值，得到2測點對應預/報警限分別為64.81/65.32 dB,88.54/88.99 dB.另取相同工況(0～30 s)和80 r/min工況(31～60 s)的總級樣本各30組用于檢驗，結果見圖1～2.由圖1～2可見，工況相同的總級樣本大多落入零假設區間，FJ01出現1次錯誤預警、1次誤報警，FJ30發生1次誤報警；80 r/min工況對應總級樣本均高出預警限，2測點分別有66.7%和100%的總級樣本被判定為故障，客觀反映了實船運行工況變化.

3.2二級檢測閾值檢驗

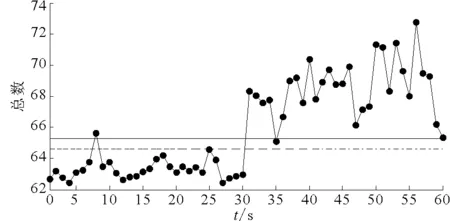
圖1　測點FJ01的總級超標檢測

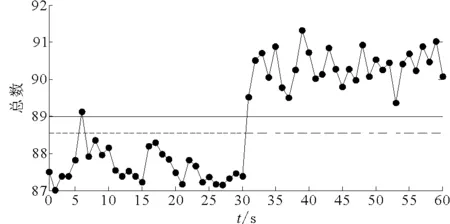
圖2　測點FJ30的總級超標檢測

針對檢測中出現的誤報警問題，引入二級閾值進行分類檢測.首先根據報警事件樣本進行報警頻次建模，取80 r/min工況下測點FJ12的數據記錄進行分析，樣本時長60 s、數量30組，統計不同樣本時長內報警次數均值見表1.由表1可見，30組樣本平均報警概率為1/12；若故障檢測周期以5 s計，則對應參數λ應等于0.417.

表1　隨機報警事件報警頻次統計

(9)

查閱泊松分布概率密度分布可知，k0=2，即以置信度95%認為正常工況下5 s內隨機報警事件次數不應超過2次；超過2次的小概率事件可判定為聲學故障.相同算法應用于測點FJ30得閾值k0仍等于2.

選取試驗記錄中包含一次設備啟動(約180 s前后)的數據樣本進行分析，檢驗二級閾值能否有效區分設別運行工況改變(即聲學故障)與隨機報警事件.首先根據區間估計原理建立一級檢測閾值，檢測結果見圖3a)，4a)，檢測結果中伴隨大量誤報警事件，檢測效果較3.1變差；在此基礎上引入二級閾值k0=2進行分析，結果見圖3b)，4b).由圖可見FJ12，FJ30的第36樣本點(與180 s對應)出現報警，說明聲學故障得以保留；除此之外僅FJ12的13號樣本點出現超標，其余樣本點均判定為正常，誤報警事件得到明顯抑制.

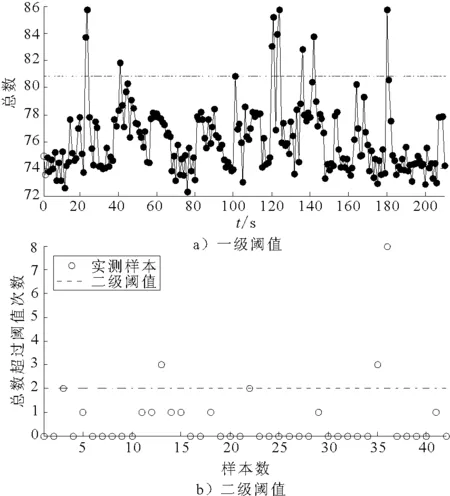
圖3　測點FJ12的二級閾值檢測效果

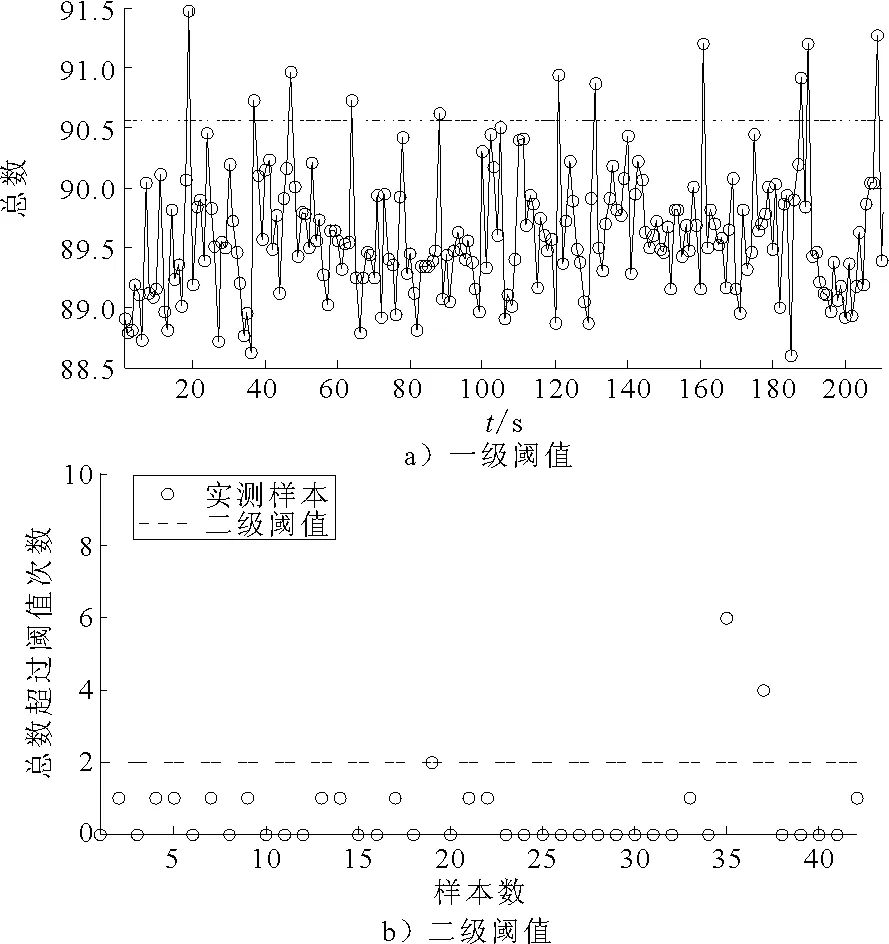
圖4　測點FJ30的二級閾值檢測效果

4結束語

本文分析了潛艇測點級聲學故障的檢測方法，根據區間估計原理建立了故障檢測基本流程，針對實船應用中的隨機報警事件干擾提出了基于報警事件頻次建模的二級閾值檢測法，并通過實船測試數據進行了算法驗證.數據分析顯示，該方法能夠有效區分典型聲學故障與隨機報警事件，顯著降低正常工況下監測結果中的誤報警問題，能夠為聲學故障修復決策提供更優的決策依據.

參 考 文 獻

[1]艦船動態隱身性能監測與管理[M].武漢:海軍工程大學出版社,2013.

[2]王之程,陳宗岐,于沨,等.艦船噪聲測量與分析[M].北京:國防工業出版社,2004.

[3]SETO M L.Application of tonal tracking to ship acoustic signature feature identification[J].Journal of Vibration and Acoustics,2011(133):1-3.

[4]徐榮武,何琳,湯智胤,等.水下航行器聲學故障檢測中距離有效性的評價[J].振動與沖擊,2011,5(30): 184-187.

[5]STRUNK W D.Considerations for the establishment of a machinery monitoring and analysis program for surface ships of the U. S. navy[C]. Proceedings of the 6th International Modal Analysis Conference,Orlando,FL,USA,1988:914-920.

[6]鄧秭珞.監測與控制聲特征信號的傳感器和作動器網絡[J].國外艦船工程,2005(9):17-19.

中圖法分類號：TP277

doi:10.3963/j.issn.2095-3844.2015.01.017

收稿日期：2014-11-09

Research on the Detection Algorithm of Sensor-level Acoustic Fault
Based on the Modeling of Alarming Frequency and Number
REN Anmin1,2)HE Lin1,2)CHENG Guo1,2)

(InstituteofNoise&Vibration,NavalUniversityofEngineering,Wuhan430033，China)1)

(NationalKeyLaboratoryonShipVibration&Noise，Wuhan430033，China)2)

Abstract：The detection algorithm of sensor-level AF was discussed in this paper,including the detection flow of frequency band energy overranging based on interval estimation theory.For solving the disturb of Arbitrary Alarm Events(AAE) to detection efforts of normal conditions, the double stages threshold was settled by alarm frequency and number modeling based on Poisson distribution,and algorithm effectiveness was verificated through noise measuring data onboard. The results showed that AAE could be distinguished from AF alarm under normal conditions using the algorithm, which could supress the false alarm effectively.

Key words：acoustic fault；frequency band energy；arbitrary alarm events；poisson distribution；double stages threshold