商業銀行匯率風險量化研究

劉飛　鄭曉亞

[摘要]本文應用有別于業界普遍采用的正態或對數正態分布函數量化研究中國商業銀行參與國際外匯市場所主要涉及的匯率收益率的風險特征，以期為處于國際化擴張中的商業銀行識別、計量與處置匯率風險提供參考。基于正態分布與非對稱拉普拉斯分布函數的比較實證研究表明，后者能夠更好地擬合匯率收益率尖峰、厚尾、偏態特征；進一步測度基于不同分布的匯率收益率在險價值，發現正態分布假設下的VaR顯著低估匯率風險，而非對稱拉普拉斯分布在度量匯率收益率在險價值方面更為有效。在商業銀行匯率風險管理過程中，非對稱拉普拉斯分布無疑是較為理想的選擇。

[關鍵詞]商業銀行；匯率風險管理；非對稱拉普拉斯分布：在險價值

中圖分類號：F830.9 文獻標識碼：A 文章編號：1008-4096（2015）04-0083-07

一、引言

隨著經濟全球化的日漸深入及中國企業“走出去”戰略的實施，中國企業國際化程度將日益提高。習總書記在2014年11月APEC工商領導人峰會上表示，未來十年中國對外投資將達到1.25萬億美元，這意味著中國今后的對外直接投資規模將增加3倍。國有企業、民營企業和中小企業將集群式“走出去”，在全球化背景下進行資源配置、產能合作與產業滲透。國務院隨即出臺了金融業支持企業“走出去”的一攬子措施。可以預見，隨著相關政策的逐步推進與政策效力的不斷釋放，由此衍生的跨境金融服務需求將為國內商業銀行帶來全新的發展機遇和潛在增長點。商業銀行如欲抓住發展契機，亟需為“走出去”客戶提供安全、便利、有效的本外幣跨境結算、中長期項目融資、投資并購等金融支持與延伸服務。在此背景下，深度參與國際金融市場是商業銀行有效整合國際金融資源、加速推進跨國經營活動的必要前提。

當前國際社會政治經濟環境日漸復雜，國際投融資活動愈加頻繁，國際金融市場中蘊含的市場、信用與操作風險越來越大。近十幾年來國際著名金融機構的破產倒閉案件和2007年美國次貸危機所引起的金融海嘯余波未息，如何在交易品種多樣化與風險種類多元化的國際金融市場進行跨幣種、跨市場、跨媒介資金交易，尋求交易收益與交易風險之間的有效平衡，成為國內商業銀行跨境交易執行主體與市場風險管理部門亟需加深理解的重要課題。

本文研究針對這一問題，通過實證研究，一方面，為國內商業銀行豐富跨境交易匯率風險測度指標，進而準確定位、有效衡量匯率風險提供參考；另一方面，將在工程科學、質量控制等領域得到廣泛應用的拉普拉斯分布引入金融風險管理范疇，在風險管理計量方法上進行新的嘗試與探索。

二、理論基礎與文獻綜述

1986年巴塞爾協定的補充協議《資本協議關于市場風險的補充協議》成功頒布，協議要求商業銀行必須量化市場風險并計算其相應資本金。市場風險管理的關鍵在于測度風險，即將風險定量化計算。最初的風險測度方法包括名義值法、敏感性法和波動性法等，由于涉及大量計算且不能為金融機構高管及監管人員提供一個關于整體風險的完整圖像，已越來越不能滿足金融市場測度風險的要求。這時，人們希望有一個簡單指標能夠完全反映其在某一特定市場價格變動和某一特定期間下持有一定頭寸的金融資產組合所帶來的可能損失額。在這種背景下，作為一種風險測度方法與風險測度指標，在險價值（Valueat Risk，即VaR）應運而生。匯率作為一種重要的金融市場指標，受國內外經濟形勢與外匯政策等因素的影響呈現出一定的波動性，特別是在浮動匯率制下，這種波動性顯得更加活躍，加劇了外匯持有主體①收益的不確定性，需要找到科學有效的方法來測度、管理風險。而誕生于20世紀90年代的VaR模型則為匯率風險提供了有效測度，使得外匯持有者能夠借助披露的VaR信息及時調整外匯頭寸、降低風險。

VaR將金融風險測度為一個確定的值，因其直觀簡潔的特點，廣泛應用于世界不同地區的銀行資本金（包括市場風險、信用風險和操作風險的資本金）分析與研究。VaR的計算方法主要有歷史模擬法、蒙特卡羅模擬法以及參數法三種，而實踐中通常多采用參數法。考慮到金融資產序列收益率具有典型的尖峰、厚尾、偏態特征，因而在采用參數法計算VaR時，確定合適的概率分布函數來描述這種特征，對提高VaR計算的準確性有著十分重要的意義。為此，許多學者進行了大量研究。陳守東和俞世典認為中國股票市場的收益率具有厚尾特征，在t分布和GED分布假定下的GARCH模型能夠更好地反映出收益率的風險特性。田新時和劉漢中基于Johnson分布族的非線性測度VaR。汪飛星等把PearsonⅦ分布應用到VaR模型的計算中。得到了很好的風險測度效果。王慧敏和劉國光利用跳躍式擴展模型和極值理論方法對滬深股市收益分布特征進行了研究，認為帕累托分布較好地擬合收益分布左尾部風險。潘志斌認為金融資產回報的尖峰厚尾現象可以通過g-h分布來描述，并運用g-h分布計算投資組合的VaR。黃炎龍將Skewed-t分布引入VaR的計算中，認為Skewed-t分布能更好地描述金融資產收益率序列的尖峰厚尾性和非對稱性特征。

綜觀前述研究成果，筆者發現，以前學者應用匯率收益率分布測度VaR時，較少運用非對稱拉普拉斯分布。盡管上述學者通過用其他分布來測度資產收益率分布，取得了一定進展。但是，由于多數分布形式比較復雜，有的分布函數沒有解析表達式，只能用特征函數來表示，給進一步研究帶來了很大的困難。鑒于此，本文嘗試利用Kozubowski和Podgorski提出的非對稱拉普拉斯分布對1999年1月1日至2012年2月14日三個重要發達市場國家匯率收益率數據進行分布擬合與檢驗，并基于擬合的非對稱拉普拉斯分布測度匯率收益率VaR。

三、分布模型

拉普拉斯分布誕生于1774年。因與正態分布相比擁有顯著的厚尾特征而在工程科學、質量控制、環境科學領域得到廣泛應用。近年來，與經濟金融學科相關的期權定價領域，圍繞拉普拉斯分布出現了實踐與應用：Kou在跳躍擴散模型中利用拉普拉斯分布較好地克服了基于正態分布假定推導出的傳統B-S模型的不足。在方法論方面，非對稱拉普拉斯分布在刻畫資產收益率尖峰、厚尾、偏態過程中衍生出兩種分布形式，即Kozubowski和Podgorski以及Huang等不同參數形式，兩者間的區別在于特定涵義的差異化參數。

（一）非對稱拉普拉斯分布的定義

我們稱隨機變量Yσ，μ服從非對稱拉普拉斯分布AL（μ，K，σ），假如參數μ∈R和σ≥0使得隨機變量Yσ，μ特征函數為：

四、樣本數據選取、擬合與檢驗

（一）樣本數據的選取

本文選取基于美元（USD）的三種主要貨幣英鎊（GBP）、歐元（EUR）和日元（JPY）所對應的匯率數據，利用非對稱拉普拉斯分布模型進行實證分析。考慮到歐元誕生日為1999年1月1日，為了使數據更具可比性，我們選取匯率時間序列數據從1999年1月1日至2012年2月14日，共3 422個樣本，數據來源為WIND咨詢金融終端。記P1為匯率的中間價序列，其收益率序列采用自然對數形式表示：

（二）樣本數據的主要統計量與參數估計

利用已觀測數據作為樣本，計算樣本描述統計量和參數極大似然估計值，結果如表2所示。

從表2可以看出，三種匯率的峰度遠大于3，尖峰特征比較明顯：在偏度方面，三種匯率的偏度也是一致，均表現為右偏。偏度、峰度的描述統計量表明匯率收益率并不服從正態分布，描述統計雖然不足以推導出一般性的結論，但卻能夠為進一步研究提供參考價值。為了進一步檢驗我們的判斷，利用STATA12.0軟件對樣本數據進行一種正態性的偏度一峰度檢驗，結果如表3所示。從檢驗結果可知，在1%顯著性水平下，匯率USD_JPY和USD_GBP無論是在偏度還是在峰度，抑或是把兩者結合在一起考慮都表現出顯著的非正態性。盡管在1%顯著性水平下，匯率USD_EUR的偏度（P=0.2583）不顯著，但其峰度（P=0.0000）非常顯著，當把兩者結合在一起考慮（P=0.0000）仍表現出顯著的非正態，結果如表3所示。對樣本進行KolmogorovSmirnov正態檢驗，結果與正態性的偏度一峰度檢驗完全一致。

（三）匯率收益的非對稱拉普拉斯分布參數估計與擬合圖

為了擬合非對稱拉普拉斯分布模型，我們運用最大似然估計量，分別計算三種匯率收益率分布估計參數μ、σ和κ，結果如表2所示。把其代入表1中的總體矩的理論值公式，即可得到分布特征參數的理論值，計算結果如表4所示。

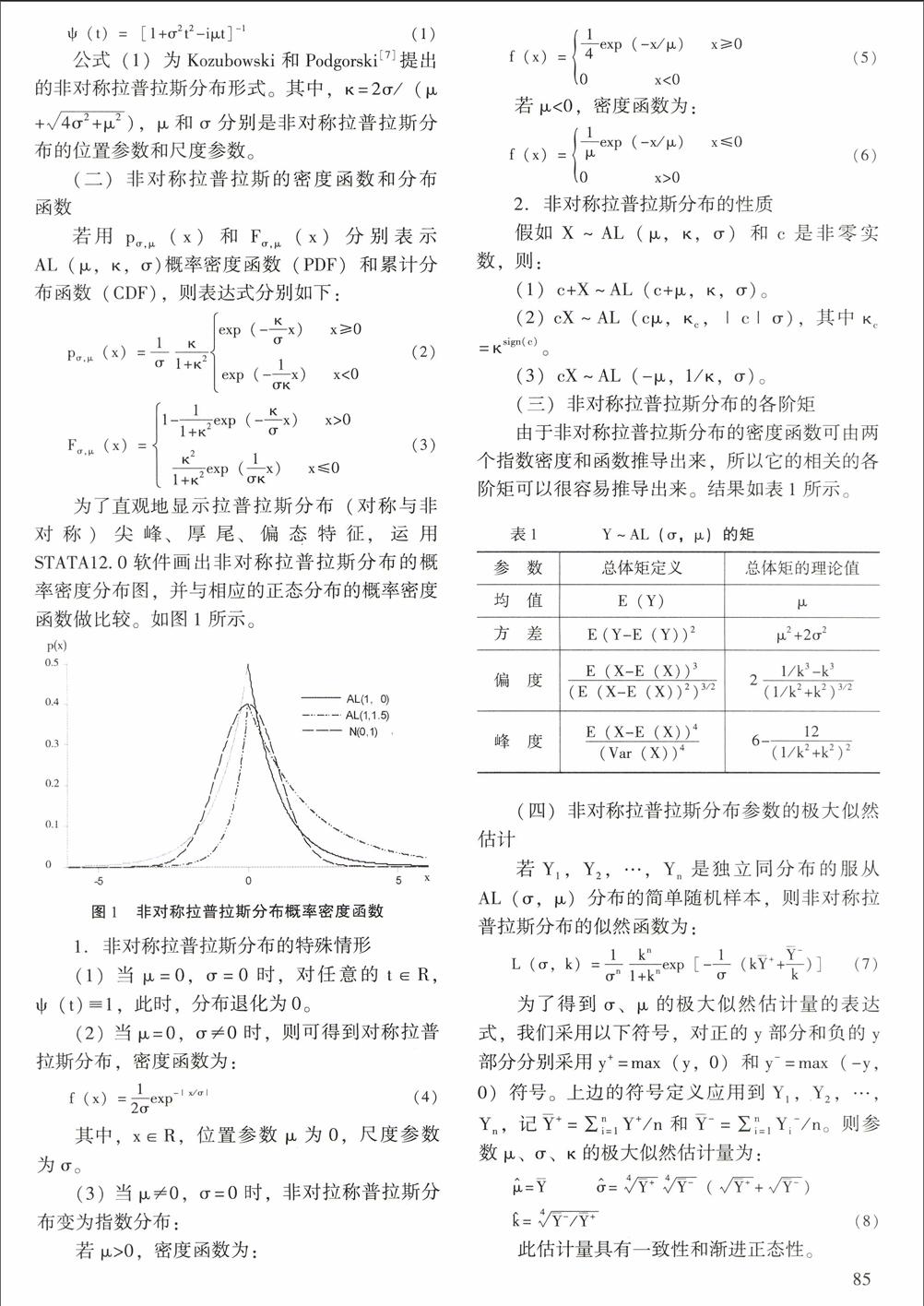
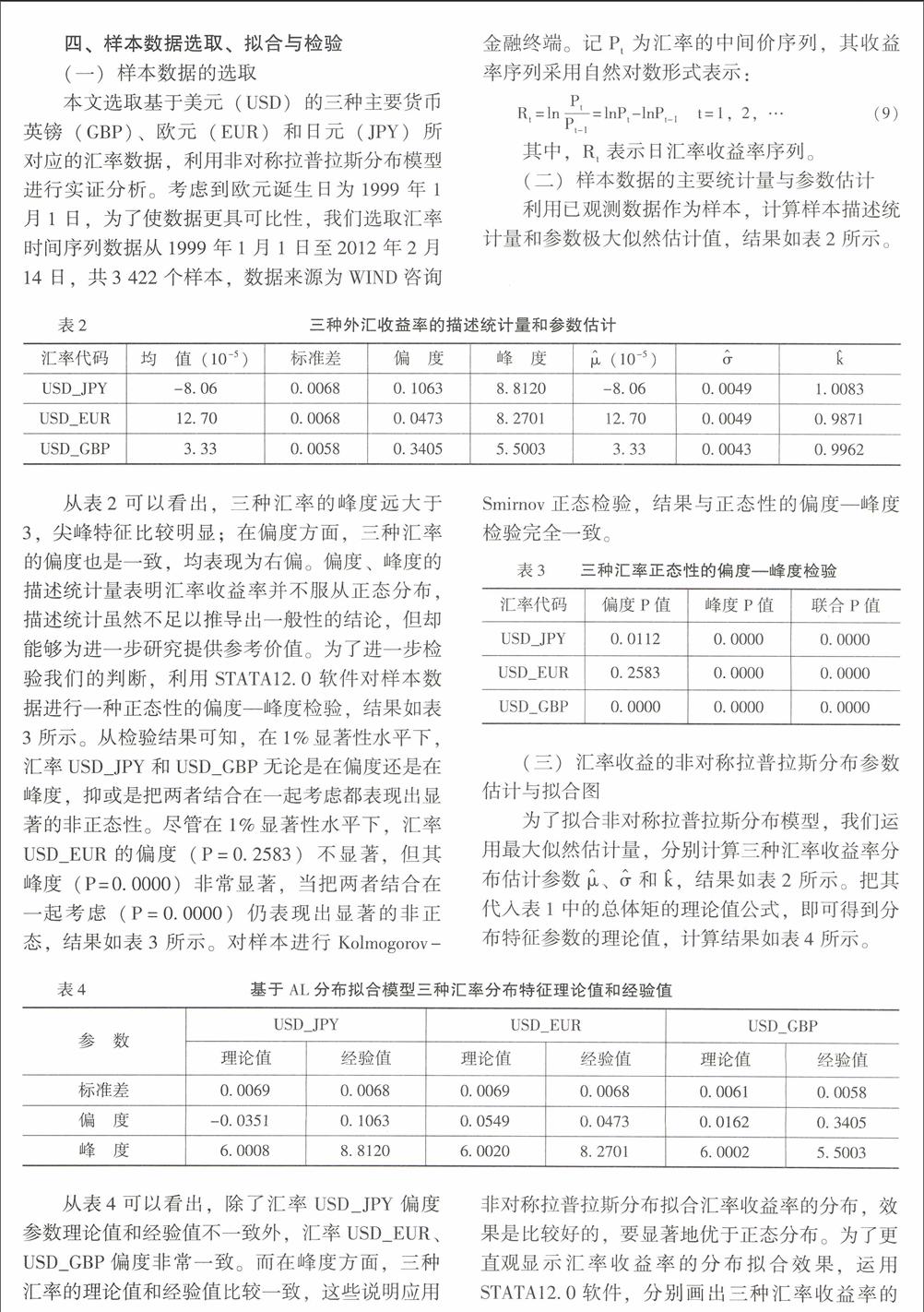
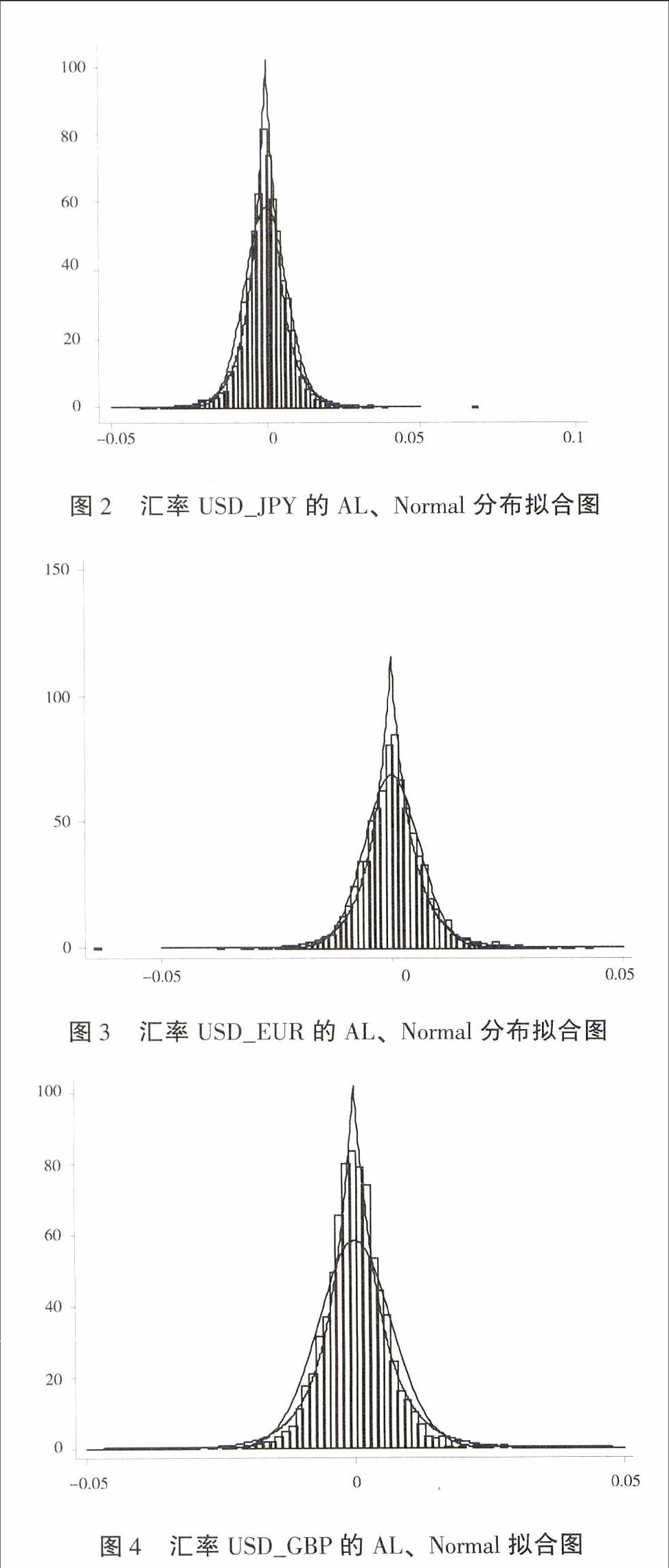
從表4可以看出，除了匯率USD_JPY偏度參數理論值和經驗值不一致外，匯率USD_EUR、USD_GBP偏度非常一致。而在峰度方面，三種匯率的理論值和經驗值比較一致，這些說明應用非對稱拉普拉斯分布擬合匯率收益率的分布，效果是比較好的，要顯著地優于正態分布。為了更直觀顯示匯率收益率的分布擬合效果。運用STATA12.0軟件，分別畫出三種匯率收益率的直方圖，并根據相應的估計參數，畫出非對稱拉普拉斯分布和正態分布的密度函數圖，再將它們疊加一起，如圖2-圖4所示。

從以上三種匯率的擬合圖以清楚地看到，非對稱拉普拉斯分布能較好地擬合三種匯率收益率分布，優于正態分布的擬合效果。使用它去擬合匯率收益率，除了匯率USD_JPY偏度不一致外，非對稱拉普拉斯分布能夠很好地擬合匯率收益率序列的尖峰、厚尾、偏態特征。

（四）非對稱拉普拉斯分布擬合檢驗

為了進一步證實上文的結論，進行Kolmogorov-Smirnov擬合優度檢驗，D為分布函數和樣本累計分布之間的K-S最大距離，用來檢驗樣本數據是否服從非對稱拉普拉斯分布，檢驗結果如表5所示。

從表5可以看出，在5%顯著性水平下，基于非對稱拉普拉斯分布三種匯率擬合檢驗的P值均大于α，因而接受原假設，即匯率收益率序列服從非對稱拉普拉斯分布。因此，運用非對稱拉普拉斯分布測度匯率收益率的VaR是合適的。

五、外匯收益率VaR測度

我們主要研究基于擬合的非對稱拉普拉斯分布如何測度匯率收益率VaR。另外，考慮到匯率收益率分布偏態特征，盡管多頭頭寸和空頭頭寸的VaR并不正好相反，但計算方法原理完全一樣，因而本文主要關注匯率收益率多頭頭寸的VaR測度。

（一）VaR的定義及其計算方法

VaR是一種利用統計思想對風險進行測度的方法，又稱為在險價值。VaR是指在一定的置信水平下，某一金融資產或證券組合在未來特定的一段時間內最大可能的預期損失。從數學角度來說，VaR可以表示為資產組合的收益率分布α分位數，表達式為：

也是就說，未來收益率只有α的概率小于等于VaR。在VaR的定義中有三個基本要素，即時間展望期、置信水平和資產收益率分布。（1）時間展望期的選擇。通常時間展望期就是指計算VaR的時間范圍。由于本文選用的是日收益率數據，故時間展望期為一個交易日。（2）置信水平的選擇。對于不同的風險類型，一般選擇不同的置信水平。置信水平越高，風險厭惡程度越大。（3）資產收益率分布的選擇。一般假定資產收益率服從正態分布，但根據前文匯率收益率分布擬合檢驗結果可知，非對稱拉普拉斯分

六、結論與政策建議

本文選取1999年1月1日至2012年2月14日國際外匯市場上三種主要匯率收益率數據，運用正態分布及非對稱拉普拉斯分布進行擬合，實證研究結果表明，非對稱拉普拉斯分布能夠比正態分布更好地擬合匯率收益率的尖峰、厚尾、偏態特征，而且非對稱拉普拉斯分布有顯性的解析表達式，具有有限的二階矩，只需兩個參數就可以確定。因此，參數估計和數字特征比較容易計算。在此基礎上本文分別測度基于正態分布和非對稱拉普拉斯分布的VaR。我們發現，正態分布假設下的VaR低估了匯率風險，而非對稱拉普拉斯分布能較好地測度匯率日收益率的VaR。為了進一步檢驗我們上述判斷，本文還采用最為常用的LR統計量進行檢驗，檢驗表明非對稱拉普拉斯分布能夠準確地測度三種匯率收益率風險。因此，對商業銀行風險管理者而言，在采用VaR風險測度技術進行尾部風險控制時，非對稱拉普拉斯分布將是較好的選擇。

匯率風險控制是一項較為復雜的系統工作。商業銀行如需進一步提高匯率風險管理水平，在有效測度匯率收益率VaR的基礎上仍需做好以下工作：第一，明確匯率風險控制目標。利用非對稱拉普拉斯分布測度匯率收益率的VaR，制定可浮動的匯率收益率VaR區間，準確計算外匯風險敞口頭寸，根據模型估計結果。檢查外匯交易頭寸的風險程度并采取必要的交易措施進行市場操作，將匯率風險控制在設定范圍內。第二，優化匯率風險管理技術。匯率風險控制的基礎在于理論模型，而理論模型與現實之間存在一定的差距，需要定期調整和改進模型。應根據外匯市場交易情況和自身交易頭寸信息，結合宏觀經濟狀況和國內外市場與行業變化形勢對模型設定進行優化，以提升模型預測能力。第三，進行匯率風險績效評價。外匯市場交易中，僅利用VaR反映匯率風險狀況，可能出現交易人員過度交易現象，影響外匯收益。需引人合理的附加措施，使得金融機構風險與收益直接關聯，能較為真實地反映交易人員業績。此外，強化機構持有者的內部審計和管理機制也是減少匯率風險的重要措施。

（責任編輯：韓淑麗）