初中數學課堂例題教學初探

林朝樂

【關鍵詞】初中數學 課堂例題

教學策略

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2015）12A-

0100-01

例題教學是學生理解、掌握和運用數學概念、法則、性質、定理、方法、思想的必要過程，是學生將數學知識和技能轉化為能力的必要途徑和手段。有效的例題教學，既能使學生掌握數學基本知識在解決問題中的應用，也能加深對基本知識的領會和理解，更好地掌握解題技巧，促進數學素養的提高。如何設計例題教學，是一個值得我們深思的課題。

一、切中要害舉例，抓住重點難點

雖然例題教學在課堂教學中的作用比較重要，但卻不能占據太大的比重，也就是說例題的教學要少而精，盡可能多地涵蓋剛學習的知識內容，這就對教師篩選例題的內容提出了很高的要求。因此，教師在設計例題時應切中要害，抓住重點，突破難點。

例如，為了向學生們強調數形結合思想的重要性，筆者在教學中引入了這樣一道例題：一個面積是1的矩形，它的周長能夠取得的最小值是多少？一個周長是3的矩形，它的面積能夠取得的最大值又是多少？這兩個問題看似簡單，但當學生們列出了xy=1和2（x+y）=3這兩個方程之后便會發現，想要靠目前所掌握的代數知識，很難輕松找到最值。于是，筆者引導學生將上述兩個方程分別變形為y=和y=-x+，并一一畫出反比例函數與一次函數的圖象（如右圖），周長的最小值與面積的最大值也就出現了。在這里，筆者特意選擇了一道過程并不復雜的例題，從而讓學生們的注意力不會向理解題目含義等方向分散，“數形結合”這一教學重點也就能被學生所關注了。可見，切中要害的例題內容選擇對于推進課堂教學的效果是十分顯著的。

二、適度靈活處理，不拘泥于課本

很多教師認為，既然例題是依據本次課堂教學的內容而設定的，對其進行解答時也應當嚴格按照本次教學內容中的思想方法展開。這種做法雖然可以強調例題的針對性，但也會造成學生的數學思維過于禁錮。適度地走出課本內容，對例題進行多角度的靈活處理，不僅能夠將課堂內容講解清楚，還可以開辟出更多的思考路徑。

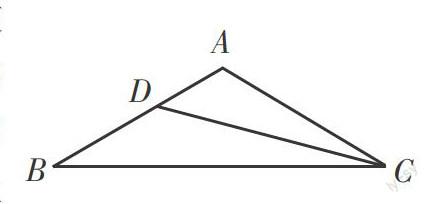
例如，在教學“等腰三角形”的內容時，筆者設計了這樣一道例題：如下圖所示，在△ABC中，∠A=100°，AB=AC，CD是∠C的平分線。求證：BC=CD+AD。這道題的證明方法很多，講解時，筆者先向學生們講解了通過在BC上截取CD=CE，以D為圓心并以DE長為半徑作弧交BC于F，這樣兩次構造等腰三角形來轉移等量線段的方式來證明的思維過程。這是緊貼等腰三角形的知識內容展開的，筆者將大部分精力放在了對于這種解題方法的分析上。隨后，筆者又向學生們介紹了在BC上截取CD=CE，使得A、D、E、C四點共圓來證明的方式，以啟發學生的其他思路。

當然，在運用多種方式解答例題時，教師也要把握好著力輕重的分布。依據本次教學內容而產生的解題方法，必然是教師所要強調的重點。其他解題方法則作為輔助方法即可。處理好這樣的主次關系，才不會讓課堂教學偏離主線。

三、及時調整視角，順應學生心理

學生是數學知識的最終接受者，自然也就成為了初中數學教學的主體。因此，例題在為課堂教學服務的同時，實際上也是在為學生理解知識服務。由此，學生自身對于例題的感受如何，也就成為了評價例題教學開展效果的重要指標。教師在設計例題時，除了要讓例題的內容與本次教學相契合，還要及時關注學生的心理，讓例題得以最大程度地被學生接受。

例如，在教學“方程”這一比較抽象的內容時，筆者設計了聯系實際的例題：①有一塊四周鑲有寬度相等的花邊的地毯（如下圖左），它的長是8米，寬是5米。如果地毯中央的長方形圖案面積是18平方米，則花邊的寬度是多少？②如下圖右所示，靠在墻上的梯子長度為10米，梯子頂端距離地面的垂直高度是8米。如果梯子的頂端下滑了1米，則梯子的底端移動了多少呢？這兩道例題，讓學生在解決實際問題當中感受到了方程的應用價值，理解并接受這一思想方法也就自然了很多。

總之，想要通過例題的方式實現有效的初中數學教學也不是隨意為之的。一要保證例題的存在是有意義的，是緊貼本次教學的重點難點的；二是對于例題的思考也不能被本次教學內容完全限制，不要讓其失去啟發學生思維的功能；三是站在學生的角度設計和處理例題，讓學生們最大化地接受知識。

（責編 林 劍）