大型撓性太陽帆板的閉環驅動控制技術研究
施桂國,王 赟,朱慶華,胡恒建
(1.上海航天控制技術研究所,上海 200233;2.上海航天技術研究院,上海 201109)
0 引言
傳統航天器太陽帆板驅動以步進電機作為執行機構,采用開環控制方式,具有實現簡單和控制精度適中的優點。但隨著未來以大慣量和大撓性為特點的大型新型帆板在空間站、太陽能發電衛星和超大型雷達天線衛星等大型航天器中的逐漸應用,開環控制模式已不能滿足航天器對帆板跟蹤提出的轉速穩定性和位置精度的要求[1]。因此,高精度帆板驅動控制將會采用閉環控制模式,如國際空間站的α太陽帆板驅動系統已采用了閉環控制模式[2]。閉環控制是大型撓性帆板驅動的關鍵技術之一,與傳統開環控制相比,其設計中需考慮的因素更多,尤其是要協調帆板撓性抑制與跟蹤控制性能間的關系。針對大型航天器采用大型撓性帆板的背景需求,考慮帆板撓性、齒輪減速器間隙和摩擦力等工程要素,本文對大型撓性帆板的閉環驅動控制技術進行了研究。
1 系統剛撓耦合動力學建模
1.1 驅動系統組成
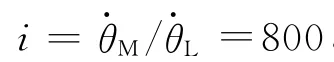
系統動力學模型是控制器設計依據和應用對象,建模時需重點關注帆板撓性、齒輪傳動間隙、摩擦力矩等非線性因素。
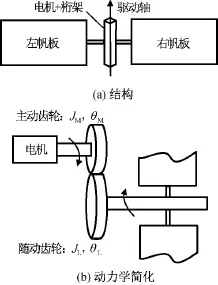
圖1 帆板驅動系統Fig.1 Solar panel driving system
1.2 齒輪傳動動力學模型
因存在加工和裝配誤差,且為存儲潤滑油,一對相互嚙合的齒輪總有一定的齒側間隙。齒隙的滯環非線性特性如圖2所示,它對伺服控制系統的影響主要有:降低了系統的跟蹤精度;使系統動態響應滯后并振蕩,降低了系統的穩定裕度。由圖2可知:當主動齒輪未越過半齒隙α時,兩齒輪間無力矩傳遞,只有當主動齒輪越過半齒隙α與從動齒輪接觸后,兩輪間才有力矩傳遞,因此可用死區模型描述齒輪副間的力矩傳遞關系。
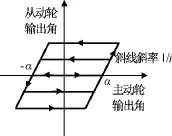
圖2 齒輪副轉角滯環特性Fig.2 Backlash characteristics of gear pair
認為齒輪副的運動只有扭轉運動而無橫向運動,暫時忽略齒輪運動時由支承軸承產生的摩擦的影響,將齒輪力矩傳遞關系等效為如圖3所示的非線性彈簧和阻尼,則可建立齒輪傳動動力學模型為
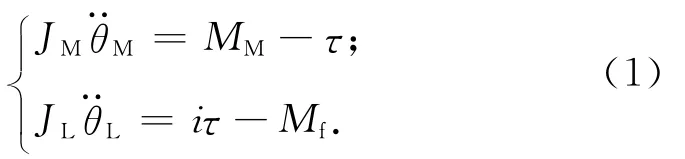
式中:τ為主從動齒輪間的彈性力和阻尼力;Mf為摩擦力矩[3]。用死區模型,τ可表示為
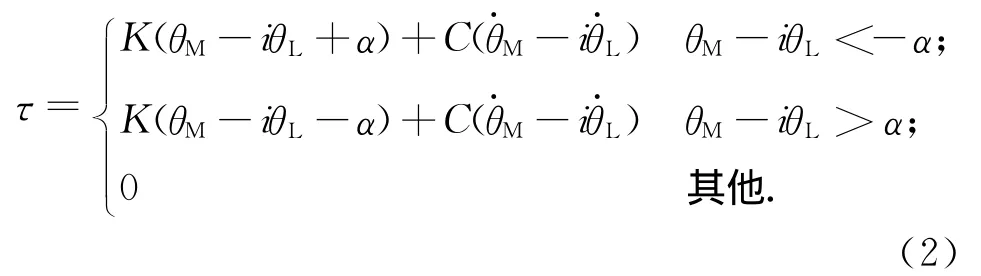
式中:C,K分別為等效阻尼和等效剛度系數;α=0.06°。
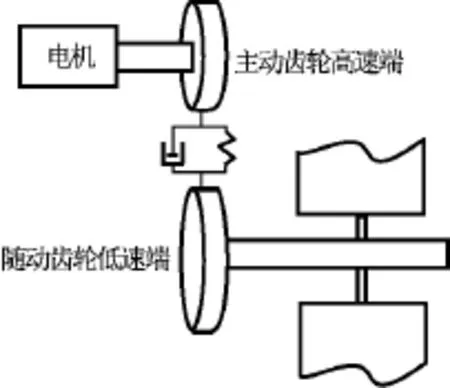
圖3 齒輪傳動的阻尼+彈簧力矩模型Fig.3 Damp+spring dynamics model for gear transmission
Mf主要存在于從動齒輪與其支撐面間,認為由靜摩擦力矩和動摩擦力矩組成,有

式中:為一個非常大的正數。
1.3 帆板驅動系統動力學模型
因帆板的撓性十分明顯,故完整的系統動力學模型還需考慮帆板的撓性振動。基于系統轉速和帆板彈性變形均為小量的假設,在齒輪傳動模型式(1)的基礎上添加撓性耦合力矩,得系統動力學模型為

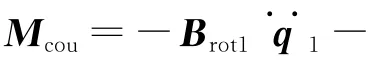
取帆板阻尼比為0.005,由式(4)可得系統從低速端力矩到帆板轉角的開環伯德圖如圖4所示。由圖可知:系統具有模態密集、甚低基頻和撓性強烈的特點。
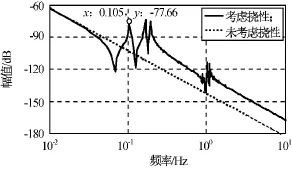
圖4 系統從低速端力矩到帆板轉角的開環伯德圖Fig.4 Open-loop Bode diagram from moment to solar panel angle
2 控制策略設計
2.1 頂層設計
帆板驅動系統的轉動慣量巨大,存在傳動間隙、摩擦力和大撓性等多種影響驅動控制性能的因素,且航天器穩態飛行時對帆板的角度跟蹤精度和轉速穩定性要求較高,故驅動控制器采用閉環模式。
控制帶寬和穩定裕度是控制器設計的基本考慮要素:為使系統有良好的過渡過程,系統的相角裕度為30°~70°、幅值裕度>6dB較合適;對撓性體,控制帶寬需根據撓性基頻而定,常將控制帶寬設計成基頻的幾分之一。此外,對帶大撓性負載系統,加入控制器后在整體模態頻率處的增益仍較大,需減小該處的增益,工程上降低至-10~-20dB即可。
系統的控制原理如圖5所示。圖中:由于電機電流環的帶寬遠大于系統帶寬,因此將電流環當作增益為Kt的比例環節,且將齒輪傳動當作比例系數為i的比例環節,測量信息反饋采用慣性濾波器。
2.2 控制器設計
控制器采用傳統PID控制律,其中:比例項P用于減少跟蹤誤差;積分項I用于將系統從原來的Ⅱ型系統提升為Ⅲ型系統,消除跟蹤對輸入信號的跟蹤靜差,以及消除由常值干擾力矩造成的跟蹤靜差。PID控制參數用二階系統設計理論計算。
2.3 撓性抑制濾波器設計
帆板撓性抑制濾波器用于壓制系統的主要振動模態增益,以避免激起大撓性振動,并可拓寬控制帶寬。因本文研究的帆板難以安裝壓電陶瓷等硬件以實現主動撓性抑制,故采用了濾波器抑制技術。撓性抑制濾波器相對壓電陶瓷簡單,主要有陷阱濾波器和四階 Bufferworth低通濾波器等[2、5]。這些濾波器在壓制主要振動模態增益的同時,存在相角延遲的弊端,將降低系統的相角裕度,嚴重時會使系統失穩。由于控制帶寬、抑制模態增益和穩定裕度相互制約,需折中選擇合理的控制器和濾波器的參數。綜合考慮,本文選用的陷阱濾波器為
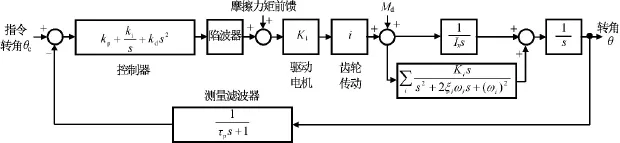
圖5 閉環控制系統原理Fig.5 Closed-loop control principle for solar panel driving system
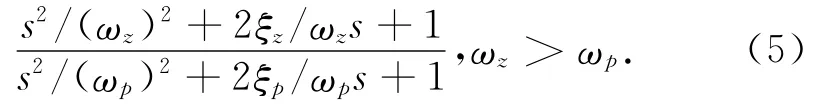
2.4 摩擦力矩前饋補償
從動齒輪與其支撐間的摩擦力是系統最主要的摩擦力,它對系統的動態性能有重要的影響:受較低控制帶寬的制約,系統從開始接受轉動指令后的一段時間中,由于系統輸出力矩被靜摩擦力矩平衡,帆板實際上仍是靜止的,只有等輸出力矩超過靜平衡力矩時帆板才真正被啟動,因此系統存在較明顯的響應延遲。對此本文采取了摩擦力矩前饋補償措施,基于工程簡便性等考慮補償了動摩擦力矩[6]。實際上,補償精度不需很高,補償掉大部分摩擦力矩就能提高系統響應速度。
系統加入控制后從低速端力矩到帆板轉速的開環伯德圖如圖6所示。由圖可知:系統的頻域指標均符合設計要求:系統的相角裕度和幅值裕度分別為30.9°(頻率0.015Hz處)和6.2dB(0.026Hz處);加入陷波器后,系統的最大模態增益從15.5dB降至-14.9dB,有效抑制了帆板撓性。

圖6 系統從低速端力矩到轉速的開環伯德圖Fig.6 Open loop Bode diagram from moment to solar panel angle speed
3 數學仿真驗證與分析
用Simulink軟件對帆板驅動控制策略跟蹤軌道角速度的工況進行仿真驗證。設帆板轉角測量誤差0.01°(3σ)的零均值白噪聲,帆板轉速由轉角微分得到,設其為誤差0.1(°)/s(3σ)的零均值白噪聲,仿真結果如圖7~13所示。

圖7 帆板位置跟蹤結果Fig.7 Tracking angle of solar panel
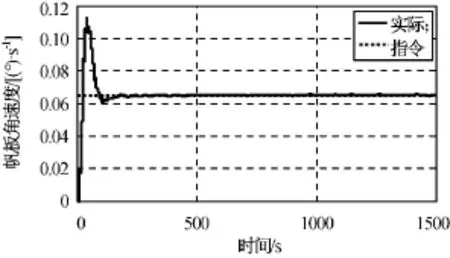
圖8 帆板角速度跟蹤結果Fig.8 Tracking angle speed of solar panel
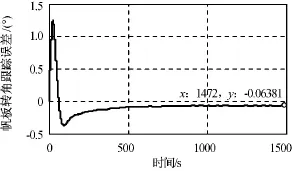
圖9 帆板角位置跟蹤誤差Fig.9 Tracking angle error of solar panel
由仿真結果可知:通過對動摩擦力矩進行前饋補償,帆板啟動時間從80s左右降至20s左右;系統進入穩態后的帆板轉角和轉速跟蹤誤差分別優于0.1°,0.001 (°)/s;穩 態 時 電 機 實 際 輸 出 力 矩 約0.15N·m,即使考慮齒輪減速器70%效率,也遠小于額定力矩1N·m;撓性抑制濾波器對抑制帆板撓性振動明顯,利于降低作用于航天器本體的干擾力矩,也利于帆板的結構安全。
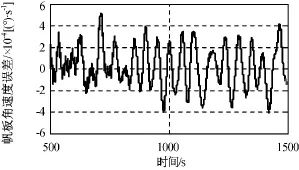
圖10 帆板角速度跟蹤誤差Fig.10 Tracking angle speed error of solar panel
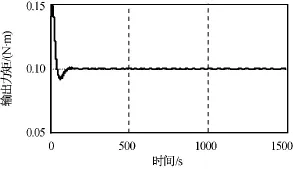
圖11 電機輸出力矩Fig.11 Output moment of motor
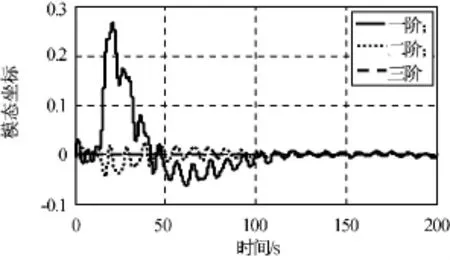
圖12 帆板主導模態坐標Fig.12 Main flexible mode axis of solar array
4 結束語
為提高大型航天器撓性帆板的跟蹤控制精度,并減少耦合到航天器本體姿態的帆板轉動加速度,本文建立了含撓性振動、減速器間隙和摩擦力等實際工程要素的系統剛撓耦合動力學模型,研究了基于PID控制器+撓性抑制濾波器+摩擦力矩補償的控制策略。數學仿真結果驗證了控制策略的可行性,穩態時帆板轉角跟蹤誤差優于0.1°,轉速穩定度優于0.001(°)/s,且帆板撓性抑制效果明顯。該控制方案有一定的工程應用價值。
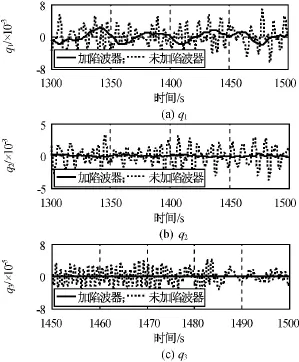
圖13 撓性抑制濾波器效果Fig.13 Suppression of solar panel flexible vibration
[1] LANE S A,MURPHEY T W.Overview of the innovative space-based radar antenna technology program[J].Journal of Spacecraft and Rockets,2011,48(1):135-145.
[2] LIN T W,COOPER P A,AYERS J K.Structural dynamic interaction with solar tracking control for evolutionary Space Station concepts[R].NASA-TM-107629,1992.
[3] 周金柱,段寶巖,黃 進.含有齒隙伺服系統的建模與對開環頻率特性的影響[J].中國工程機械,2009,20(14):1722-1726.
[4] 屠善澄.衛星姿態動力學與控制[M].北京:宇航出版社,1999:163-184.
[5] WIE B,LIU,Qiang,BAUER F.Classical and robust H (infinity)control redesign for the Hubble space telescope[J].Journal of Guidance,Control,and Dynamics,1993,16(6):1069-1077.
[6] 于志偉,曾 鳴,喬大鵬.采用復合控制的直流力矩電機摩擦補償[J].電機與控制學報,2008,12(9):539-544.

