一種改進的Bursa模型在坐標轉換中的應用

陳博，黃翔，李瀧杲，邢宏文

(1. 南京航空航天大學 機電學院，江蘇 南京 210016；2. 上海飛機制造有限公司航空制造技術研究所，上海 200000)

?

一種改進的Bursa模型在坐標轉換中的應用

陳博1，黃翔1，李瀧杲1，邢宏文2

(1. 南京航空航天大學 機電學院，江蘇 南京 210016；2. 上海飛機制造有限公司航空制造技術研究所，上海 200000)

摘要：在數字化測量中經常面臨坐標轉換的問題，轉換參數在很大程度上影響著最終測量精度。在采用bursa模型求取轉換參數時一般是通過3個以上公共點利用最小二乘法求取，但其中的系數矩陣往往是病態的，使轉換參數并不可靠。現采用7參數法，對布爾沙模型進行泰勒展開，建立了適用于大旋轉角的線性化坐標系轉換模型。

關鍵詞：坐標轉換；最小二乘；bursa模型；轉換參數

目前數字化測量在我國飛機外形及零部件檢測中應用越來越廣，正逐步取代舊式的、利用模線樣板等工藝裝備檢測方式。在獲取零部件外形高精度數據后與設計數模進行分析對比，一方面為現有工藝下的外形品質提供可靠的數字化評價，另一方面通過大量檢測結果的統計分析，可以找出影響飛機零部件品質的關鍵因素，進而建立檢測結果和誤差影響因素的統計圖表，為工藝的設計與改進提供理論和實踐參考，從而實現飛機零部件的制造品質持續提升[1]。

使用激光跟蹤儀、激光雷達等數字化測量手段可以獲取高精度的測量數據，但是當被測工件超出其測量范圍時，測量儀器不確定度也隨著測量距離的增加而增加，從而導致測量精度的下降。如Leica AT901 B激光跟蹤儀的測量不確定度為±15 μm+6 μm/m，根據現場應用情況，測量長度一般應<10 m。為解決這一問題常采用的方法是使用多臺測量設備建立統一空間計量網絡USMN(unified spatial metrology network)。這樣就會涉及2個空間直角坐標系的轉換問題，目前最常用的空間直角坐標系的轉換通常用含有7個轉換參數的布爾沙模型，這樣在轉換計算轉換參數的過程中，需要至少3個公共基準點。但是這一模型一般是只適用于2個坐標系小角度的坐標轉換。但在實際使用中公共點位情況比較復雜，測量設備可能會以任意的姿態放置在地面上或工件上進行測量，所以2個坐標系之間的坐標軸之間的夾角一般不是微小角度。陳宇[2]等研究了基于7參數的非線性最小二乘法的坐標系轉換算法，劉東明[3]等研究了13參數的大角度三維坐標系轉換方法。現針對傳統的統一空間計量網絡有檢測效率低、精度差的問題，采用激光雷達、激光跟蹤儀等測量設備建立統一空間計量網絡，利用泰勒展開將布爾沙模型線性化，建立了適用于大旋轉角的線性坐標系轉換模型，較好地平衡了測量效率與精度問題。

1激光雷達工作原理

激光雷達是一種大尺寸、非接觸、高精度、自動化、便攜式數字化測量設備。激光雷達擁有球形測量系統如圖1所示，通過運用調頻相干激光雷達測距技術和高精度反射鏡利用紅外激光光束測得被測點的距離d、俯仰角α、和方位角β從而轉換得出被測點的三維坐標信息。被測點空間坐標計算公式為：

(1)

圖1　極坐標測量

激光雷達測距原理： 激光器在發射一束經空氣傳播到測量點并且返回的外測信號的同時, 又發射一束在定長光纖中傳播的內置信號如圖2所示 。光纖的長度與固定測量距離S相對應, 即對應于激光在空氣中傳播2S的距離。假設測量點的距離為L, 那么激光在空氣中傳播的距離為2L, 返回的激光信號較在定長光纖中傳播的激光信號有Δt的時間延遲,Δt的時間延遲產生了Δf的頻率變化, 并且Δt與Δf成正比。在激光雷達中, 可以準確地測出頻率變化Δf, 通過測量頻率變化計算出時間延遲, 最終得出被測點與激光雷達的距離d。

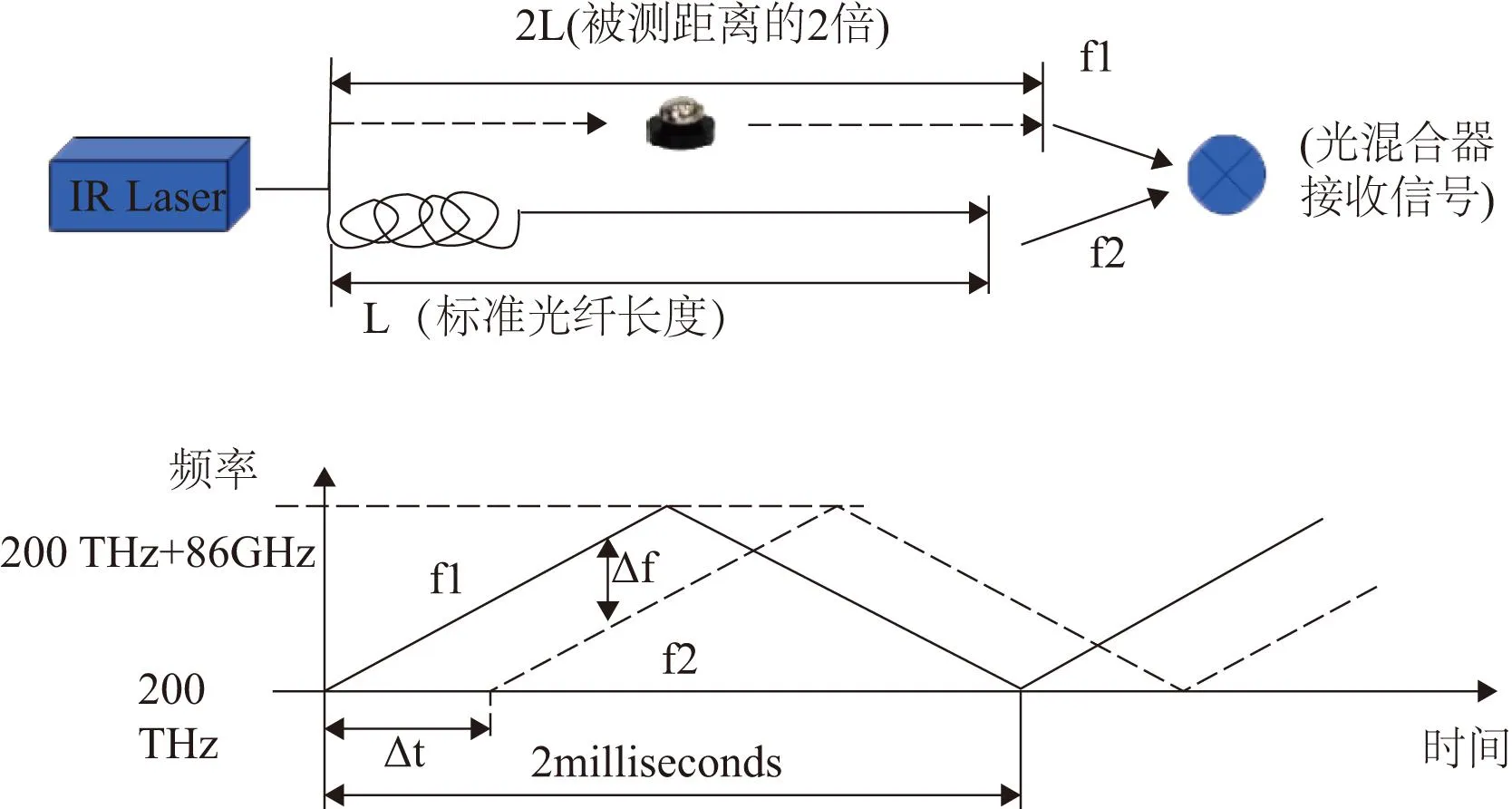
圖2　激光雷達測距原理

2坐標轉換參數計算方法

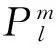
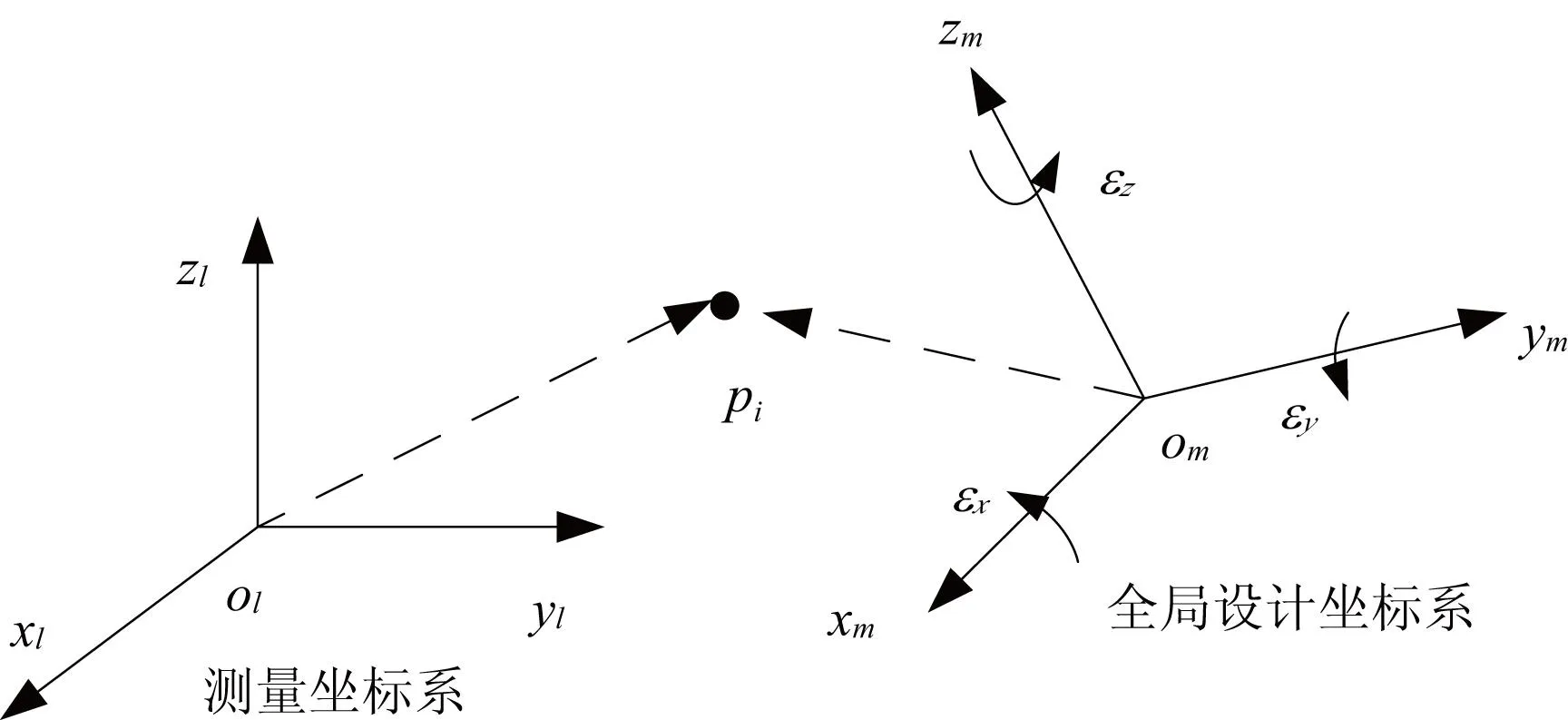
圖3　測量坐標系與全局設計坐標系關系模型

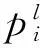
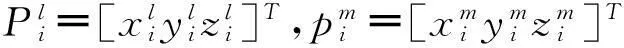
為方便描述，當旋轉角度為微小量時有：

?“Amaritudine”（苦澀），見 Cesare Ripa,Iconologia,Roma，1603，p12.

這種布爾沙模型對旋轉參數的三角函數做了近似處理，忽略了其中互乘項并記sinε=ε,cosε=1，用這種近似模型得出的旋轉參數只適用于旋轉角是微小角度的情況。如果旋轉角度不是微小角度時，使用這一模型將不能得出正確結果。而根據實際應用，測量儀器可能會以任意的姿態放置在地面或者安裝在飛機零部件上進行測量，這就意味著測量坐標系與全局設計坐標系之間的坐標軸旋轉角可能是任意角度。現將布爾沙模型進行展開，并忽略二階及二階以上無窮小項，得：

其中，上標為0的表示取近似值，d(Δx)、d(Δy)、d(Δz)、dk、dεx、dεy、dεz為參數的改正數。

上式可簡化為：

Li=BiΔC

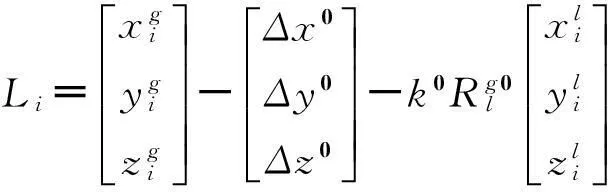
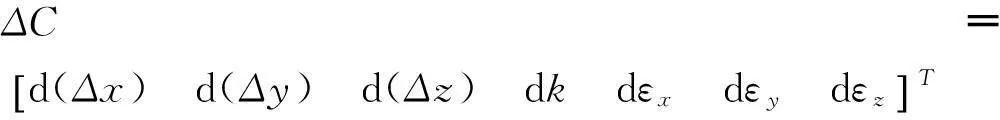
式中，ΔC為兩坐標系轉換參數的改正數，Li表示公共基準點Pi的擬合誤差，設Bi為公共基準點Pi的坐標系轉換系數矩陣。將式寫成誤差方程的形式：

Vi=BiΔC-Li

擴展至n維形式得：

V=BΔC-L

BTWV=0

聯立式和式，解算得到坐標系轉換參數的改正數：

ΔC=(BTWB)-1(BTWL)

由于各基準點可視為相同精度獨立觀測值，一般取觀測權重矩陣為單位矩陣，即W=I。轉換參數改正數的協因數矩陣Qxx和單位權中誤差估值為

QΔCΔC=(BTWB)-1

利用此方法，只要已知3個或3個以上的公共基準點的測量坐標和全局設計坐標，再為轉換參數選取合適的初值，加上每次求出的改正數，如此循環迭代，當改正數滿足一定精度時，停止迭代，便可求解出坐標系轉換參數。

3實例分析

為了驗證坐標系轉換精度，現對若干個測量點，進行坐標系轉換算法驗證試驗。選擇6個不共線的公共基準點，公共基準點的全局理論坐標和測量坐標如表1，表2所示。

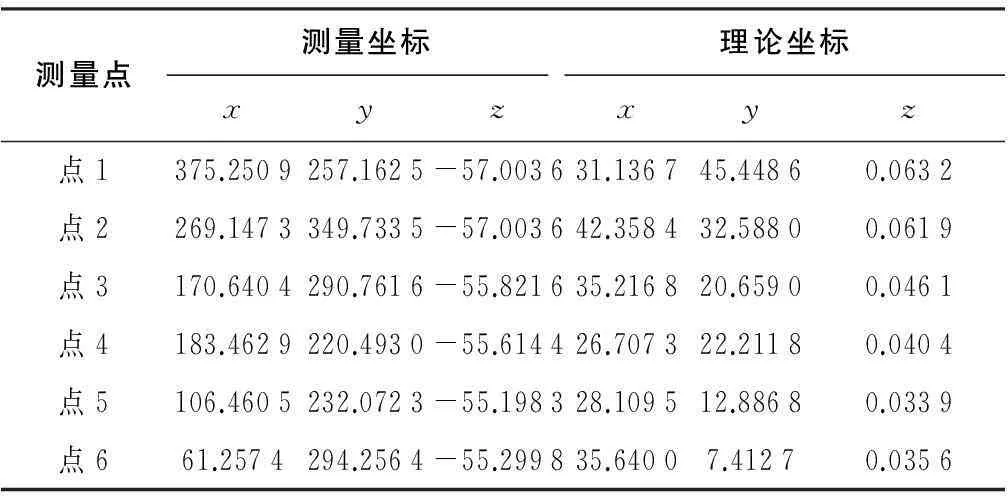
表1　理論坐標和測量坐標　單位：mm

表2　利用坐標系轉換法，求解出轉換參數

可計算得到公共基準點在全局設計坐標系中的計算坐標，比較測量點全局計算坐標與理論坐標的差，最終考察坐標系統一的計算精度如表3所示。

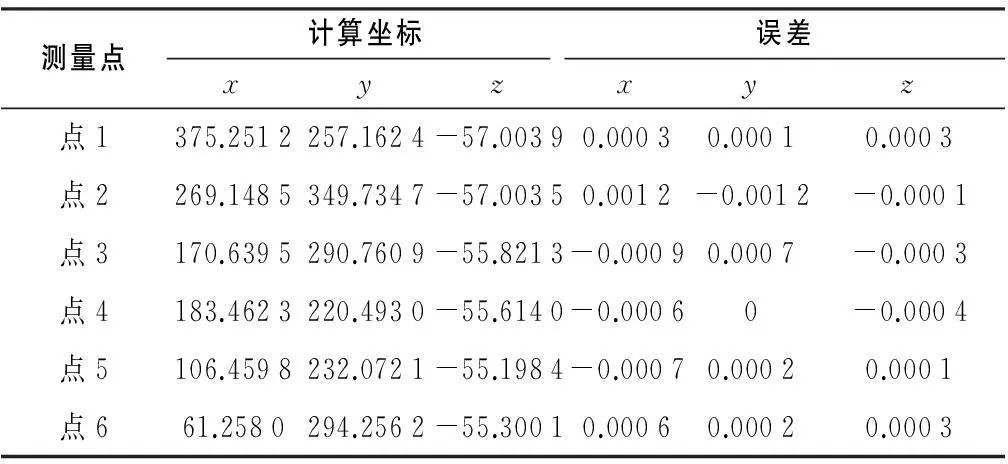
表3　計算精度表　單位：mm

實驗結果表明，該算法相對于原有算法能在較少的迭代次數內快速收斂，并精確的求解出坐標系轉換參數。該算法能行之有效的完成坐標系轉換，并具有較高的轉換精度，滿足工程應用需求。

4結語

針對傳統的bursa模型通過3個以上公共點利用最小二乘法求取轉換參數時系數矩陣往往嚴重病態，一般只適用于小角度坐標系轉換，當坐標系夾角不是微小角度時求得的轉換參數并不可靠的問題，采用7參數法，對布爾沙模型進行泰勒展開，將布爾沙模型線性化，建立了適用于大旋轉角的線性坐標系轉換模型，較好地解決了平衡測量效率與精度問題。該方法具有數值計算精度高、計算穩定性好、收斂速度快等特點，適用于任意旋轉角的坐標系轉換，能夠實現測量過程中的坐標系轉換。

參考文獻:

[1] 劉勝蘭，羅志光，等. 飛機復雜裝配部件三維數字化綜合測量與評估方法研究[J]. 航空學報，2012，(33)：1-10.

[2] 陳宇,白征東. 基于非線性最小二乘算法的空間坐標轉換[J]. 大地測量與地球動力學, 2010,(02): 129-132.

[3] 劉東明, 郭際明, 施展, 等. 大角度三維基準轉換及公共點的確定[J]. 測繪通報, 2010,(1): 11-14.

[4] Yadong Li, Peihua Gu. Free-form surface inspection techniques state of the art review [J]. Computer-Aided Design, 2004，(36).

[5] 李瀟, 尹輝. 基于最小二乘配置的三維空間坐標轉換[J]. 測繪工程, 2006, 17( 2): 16- 18.

[6] SUN Junhua. ZHANG Guangjun,WEI Zhenzhong,et al.Large 3D free surface measurement using a mobile coded light-based stereo vision[J]. System Sensors and Actuators A:Physical,2006,132(2):460-471.

[7] 劉大杰, 施一民, 過靜珺. 全球定位系統(GPS)的原理與數據處理[M]. 上海:同濟大學出版社.

[8] 陳正宇，劉春. 基于多參數正則化的空間坐標轉換與精度分析[J]. 大地測量與地球動力學，2008，(2)：1-28.

[9] Koch K R and Yang Yuanxi. Robust kalman filter for rank deficient observation model [J]. Journal of geodesy ,1998,72 (8):436-441.

Application of Improved Bursa Model in Coordinate Transformation

CHEN Bo1,HUANG Xiang1, LI Shuang-gao1,XING Hong-wen2

(1. Nanjing University of Aeronautics and Astronautics, Nanjing 210016,China; 2. Shanghai

Aircraft Manufacturing Co.,Ltd., Aeronautical Manufacturing Technology Research Institute, Shanghai 200000,China)

Abstract:In the digital measurement, the problem of coordinate transformation is often faced with. The transformated parameters may have direct influence on the measurement accuracy. These parameters can be obtained with least square at least three common points on Bursa model. Because of the ill-posed coefficient matrix, the obtained parameters are unreliable. By linearizing the model of Bursa-Wolf, Taylor is expanded and the linearized model of coordinate transformation is built, in order to be suitable for large rotation angle.

Keywords:coordinate transformation, least square, bursa model, transformation parameters

收稿日期：2014-11-27

中圖分類號：V556.7

文獻標志碼：A

文章編號：1671-5276(2015)03-0087-03

作者簡介：陳博(1989-)，男，山東菏澤人，碩士，研究方向：數字化測量。