信息熵和RBF神經網絡的發動機故障診斷

司景萍，牛家驊，郭麗娜，馬繼昌

（內蒙古工業大學，呼和浩特 010051）

信息熵和RBF神經網絡的發動機故障診斷

司景萍，牛家驊，郭麗娜，馬繼昌

（內蒙古工業大學，呼和浩特 010051）

針對汽車發動機氣門間隙異常故障，探討了應用小波分解后求各尺度小波系數信息熵，和RBF神經網絡對發動機進行不解體故障診斷的方法。由此，對某汽油發動機進行了故障模擬試驗，分別在正常工況和三種故障工況下測取了缸蓋表面振動信號。對所采集信號進行Stein無偏估計消噪處理，利用小波系數信息熵提取特征向量，進行歸一化處理，然后用RBF神經網絡對處理后的振動信號進行分類識別。發動機氣門間隙故障的診斷實例表明，在不同工況下利用小波系數信息熵提取故障特征向量、進行基于RBF神經網絡的故障診斷方法現實可行，對實現發動機不解體故障診斷具有一定的應用價值。

振動與波；故障診斷；發動機；RBF神經網絡；信息熵

汽車發動機結構復雜，工作條件惡劣，故障頻繁。發動機在運行中產生的振動、沖擊和噪聲信號所含信息豐富，是獲取發動機故障診斷信息的重要來源。據資料表明，在發動機各類故障中，氣門結構故障率占整機故障率17.1%左右[1，2]。

發動機缸蓋表面振動信號測量方便快捷，被廣泛采用。較為常用的方法是通過測取缸蓋處的振動信號，在時域或頻域提取特征向量進行故障識別，該方法診斷速度快、準確率高[3，4]。本文以DA 462型汽油發動機為研究對象，人為對其進行故障設置，采集發動機在正常和故障狀態下的振動信號，利用小波系數信息熵提取特征向量并進行歸一化處理，利用RBF神經網絡對采集的信號進行分類識別，研究RBF神經網絡在發動機故障診斷中的應用。

1 信號的去噪

汽車發動機振動的特點是振源多，振動信號復雜，屬于非平穩的多干擾信號，故需要對所采集的信號進行去噪處理。小波閾值去噪在小波分析中得到了廣泛的應用，其基本思路是：噪聲的能量分布在整個頻域內，而信號的能量只集中在有限的幾個系數上。通過小波分解后，信號的小波變換系數要大于噪聲的小波變換系數，選取適當的閾值T，當小波系數小于T時，認為這時的系數主要是噪聲所引起，將其置為零，予以舍棄。當小波系數大于T時，認為這時的系數主要是信號所引起，將其直接保留（硬閾值）或者取小波系數的范數與閾值T之間的差值，正負號由小波系數的sgn函數確定（軟閾值），然后依據得到的新的小波系數對信號進行重構，可得到去噪后的信號[5-7]。

下面以氣門間隙標準值0.15 mm、轉速為2 000 r/min時的一缸信號S為例說明信號的消噪過程。對S進行軟閾值處理，采用wden函數，對信號使用sym8小波進行5層分解。并分別采取Stein無偏估計、啟發式閾值、固定式閾值和極大極小值閾值進行消噪處理，原始信號與消噪后的信號如圖1所示。

從圖1可以看出，四種方式都使信號變得更加平滑，固定式閾值和極大極小值閾值過多地去除了信號的成分，Stein無偏估計和啟發式閾值則能在消噪的基礎上，盡可能還原真實的振動信號，達到了良好的消噪目的。所以本文采用Stein無偏估計方式進行消噪處理。

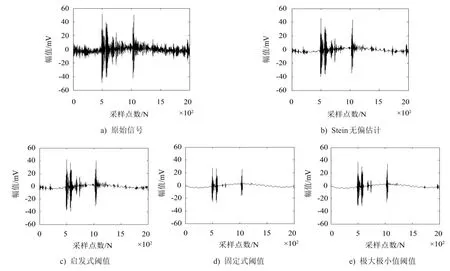
圖1 不同閾值消噪前后時域信號對比圖

2 信息熵理論

在信息論中，信息熵（也稱香農熵）表示每個信號所提供的平均信息量和不確定性量度，它能提供信號潛在動態過程中的有用信息。實際的信號中，只有單一頻率的周期信號，只包含特定的尺度小波系數，其余的小波系數基本沒有，可認定為零。而對于只包含這個特定尺度的小波系數，則認定為1，此時的小波系數的信息熵為零。通常非常復雜無序的隨機信號，它的小波系數在各個高低頻段上都有，相差不大，此時的小波系數的信息熵將接近1。由此可見，信號的概率分布越逼近這種無序的分布，其熵值也越大。信號通過小波進行多尺度變換后，所得的各尺度小波系數處理成概率分布序列，由這個序列計算得到的熵值就表征這個系數矩陣的稀疏程度，即反映了整個信號的不確定性和復雜程度[8，9]。

設信號x(t)經正交小波變換后，在i(i=1，2，…，m，m為最大尺度分解尺度)下j時刻的高頻分量系數為di,j，低頻分量系數為ai,j，則不同分辨率i=1，2，…，m下的能量信號

其中小波系數Ci(j)=[x(t)，φi,j(t)]，若把信號分解的第i層小波系數Ci(j)等分成n個小區間則有

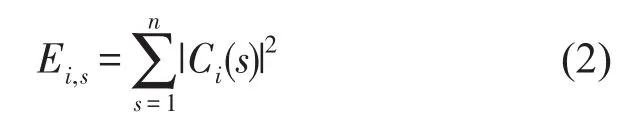
式中s為第i層小波系數的小區間數，計算對應的第s個子區間的小波能量Ei,s，并與該層小波系數總能量Ei相比求出小波能量Eˉi,s

則第i層小波系數的信息熵定義為

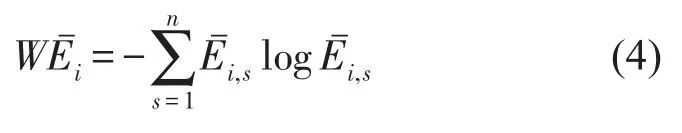
3 RBF神經網絡

與BP神經網絡相比較，RBF神經網絡有收斂速度快、訓練過程短、最終達到的均方誤差小和識別精度高等優點[10]。RBF神經網絡是一種具有單個隱藏層的三層前饋型神經網絡，其結構如圖2所示。其中第一層是輸入層，由信號源節點組成；第二層是隱含層，其變換函數為徑向對稱且衰減非線性函數RBF（徑向基函數），隱單元數由需要處理的問題所決定；第三層是輸出層，其作用是對輸入模式進行分類響應。

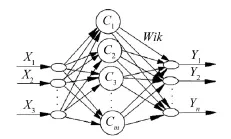
圖2 RBF神經網絡結構示意圖

RBF神經網絡由隱含層到輸出層是簡單的線性函數，在RBF神經網絡中，隱含層對輸入向量進行的是非線性變換，對輸入信號產生一個局部化的響應，而隱含層到輸出層是線性基礎上的加權，實質上就是低維空間到高維空間的變換，來達到故障分類識別的目的。

4 應用實例分析

某車用DA 462型發動機在中高速區域工作時（1 800 r/min～2 100 r/min）沖擊噪聲明顯，且有間歇熄火現象，經初步診斷其故障位置是氣門組及點火系。因此，搭建了該發動機的振動測試實驗臺架（如圖3所示）對其進行測試，人為設置了一些故障并進行基于振動信號分析的故障分類識別。

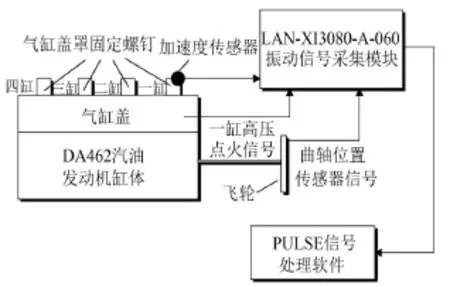
圖3 實驗數據采集測試系統

4.1 信號采集系統

試驗利用B&K公司生產的4507 B-005型振動加速度傳感器采集振動信號，傳感器安裝在一缸對應的氣缸蓋罩上的氣門螺釘處（圖4a）；曲軸位置傳感器采用桑塔納2000 GSi型ABS系統的前輪輪速傳感器，通過自制的支架安裝在正時信號觀測孔內（如圖4b），以獲得發動機的相位信號。信號采集模塊采用LAN-XI3050-A-060型4輸入通道模塊。為準確定位各缸同一時刻所處的沖程，采用元征公司的EA次級信號夾同步采集一缸高壓點火信號，采樣頻率為16.384 kHz。

圖4 傳感器安裝位置示意圖

（1）故障設置

DA 462型發動機正常氣門間隙為0.15 mm，設定氣門間隙異常值為0.45 mm。共設定三種故障：一缸排氣門間隙異常（故障1），氣門間隙正常但一缸失火（故障2），一缸排氣門間隙異常且一缸失火（故障3）。

（2）信號采集

發動機空載運行，采集一缸活塞上止點位置信號并通過軟件RPM Readout界面讀取發動機轉速，調節節氣門開度直到轉速基本穩定在2 000 r/min。

故障的模擬是在發動機正常工況信號采集完成后進行。即信號采集完成后卸下氣缸蓋罩緊固螺釘，根據故障工況的描述調節一缸排氣門間隙模擬氣門間隙故障，拔下一缸高壓點火線圈模擬失火故障，依次按故障類型進行調整并采集各故障狀況的振動信號。共采集發動機正常工況和上述三種故障狀態共四種工況的缸蓋表面振動信號。每組信號采樣點數為2 000，每種工況采集信號60組，4種工況共采集240組信號。

4.2 信號特征向量的提取

本研究在小波包變換理論基礎上，應用信息熵的計算算法進行特征量提取，步驟如下：

(1)采用“db 4”小波將一缸采集的每種模擬工況的60組信號進行4層小波包分解，得到16×60=960個小波包分解系數；

(2)選用wden函數，將小波包分解系數導入編寫好的MATLAB消噪程序中進行消噪處理；

(3)根據最低層的、經過量化處理的小波包分解系數，進行小波包信號重構，對每個重構后的信號進行4層小波包分解，得到16個正交子頻帶及16個小波包分解系數，將小波包分解系數均分為4個子區間并按式(4)計算其信息熵；

(4)將得到的特征向量進行歸一化處理，如下：

①將各頻帶小波系數的信息熵構成向量

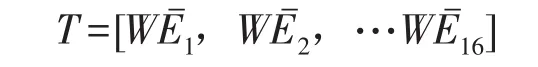
式中WEˉi為第i層小波系數的信息熵

②能量的歸一化處理

頻帶總能量為

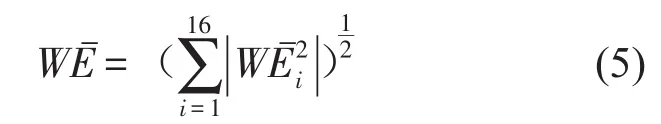
4.3 基于RBF神經網絡的故障識別

在每種工況下的60組信號中隨機挑選20組作為測試樣本，剩下的40組作為訓練樣本。依據公式(1)－(5)，可得到不同工況下訓練樣本的部分特征向量，表1所示為發動機不同工況下某一組特征向量（篇幅有限，僅列出向量前10維元素）。

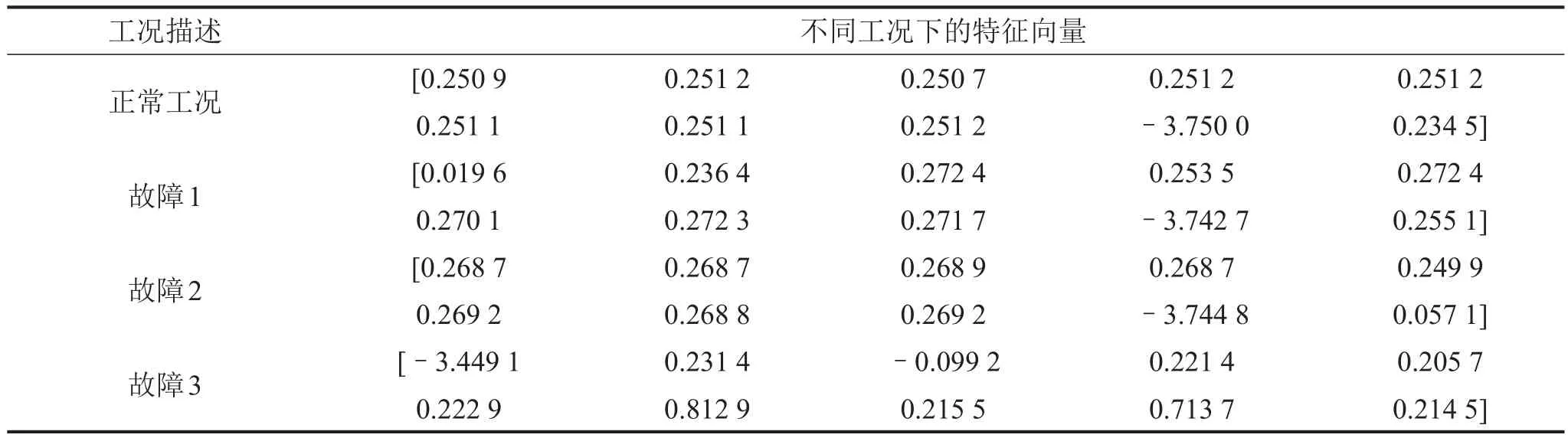
表1 不同工況下部分特征向量 單位：無量綱

圖5所示為本研究的RBF神經網絡訓練收斂圖。由圖5可以看出，本研究的RBF神經網絡訓練大約需要150步就可以完成，用時較短。

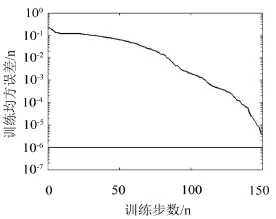
圖5 RBF神經網絡收斂圖

通過小波包分解計算得到的多尺度信息熵是一個16維的向量，可以得到神經網絡輸入層節點數為16。本文設定了發動機四種工況，由此可確定RBF神經網絡輸出層的節點數為4。通過設定不同的隱含層節點數訓練神經網絡RBF，最終確定最佳隱含層節點的個數為20。本文最終確定的網絡結構為：16個輸入節點，20個隱含層節點和4個輸出節點[11]。

表2所示為本文所設置、用于各種故障診斷的訓練樣本數、驗證樣本數與理論故障代碼對應值。

表2 樣本集的樣本數及對應故障碼 單位：無量綱

將實驗采集的60組數據中剩余20組實驗數據作為檢驗樣本數據輸入到訓練好的RBF神經網絡，由于設定了四種工況，每種工況有20組數據，因此得到的輸入向量是20×4=80個。表3為每種工況前10組檢測樣本輸出的故障結果和故障代碼。

如表3所示：數據1～10組是發動機正常工況時的輸出數據，11～20是故障1的輸出數據，21～30是故障2的輸出數據，31～40是故障3的輸出數據。

將表3檢驗樣本故障輸出代碼與表2訓練樣本故障代碼進行比較，即可獲得該發動機的運行狀態。以第26組為例：第26組故障特征輸出結果是：0.019 6、0.073 7、0.973 3、0.001 3，其中0.073 7、0.001 3、0.161 7都很接近于0，而0.973 3接近于1，得出故障輸出代碼為[0010]，這個代碼與表2中故障2即排氣門間隙正常但一缸失火故障工況下的故障代碼相同。因此可以得出：在未知發動機工作狀態的情況下，將提取的特征向量輸入到訓練好的RBF神經網絡，只要故障輸出代碼是[0010]，就可以判斷出發動機在一缸排氣門間隙正常但一缸失火狀態下工作。同理，依據輸出代碼也可以對所設置的其他故障進行判別。

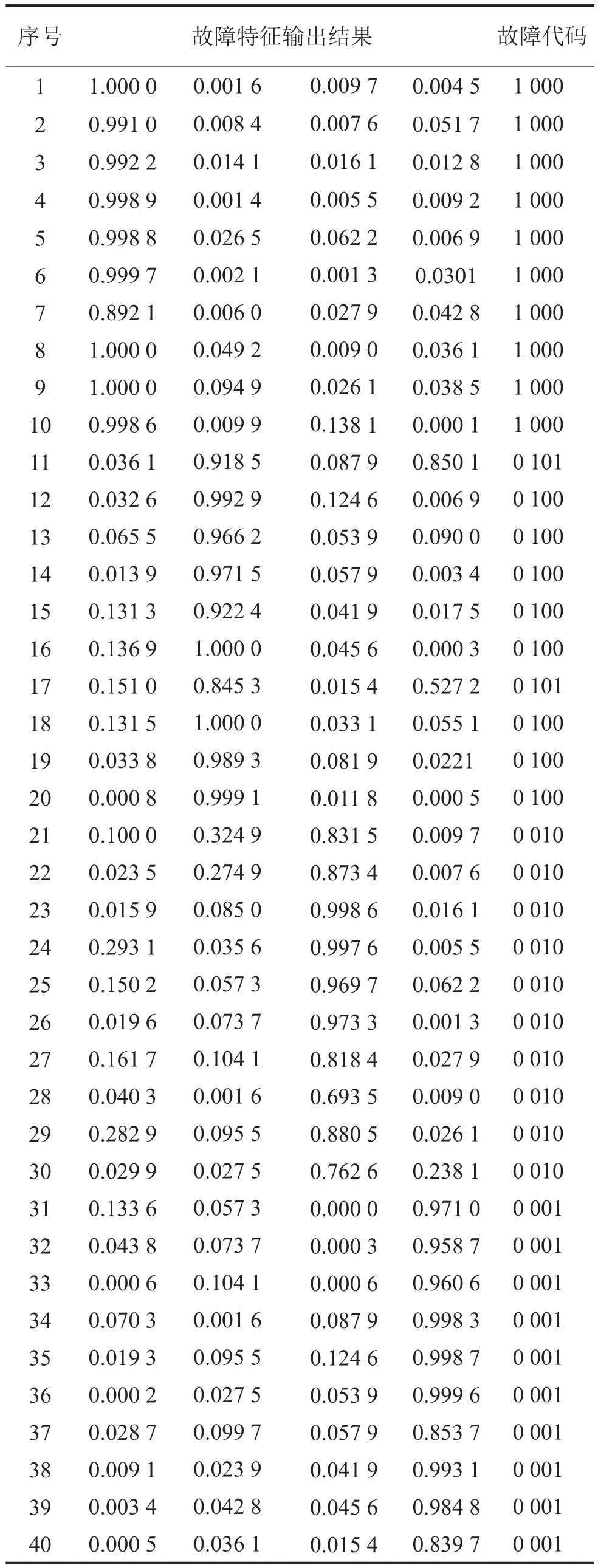
表3 檢測樣本輸出結果和故障代碼 單位：無量綱

對比80組檢測樣本故障代碼和表2所示代碼，可以得出表4的故障診斷結果。

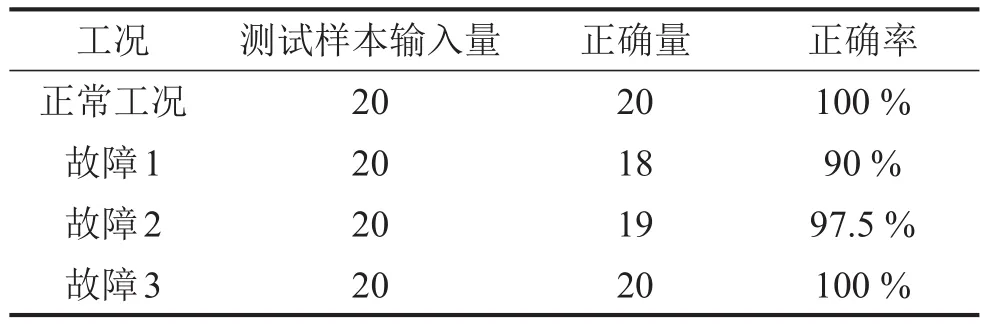
表4 檢測樣本故障輸出結果及代碼對比 單位：無量綱

從表4中，可以清晰地看出在正常工況和故障3下，RBF神經網絡的準確率達到100%，故障1狀態下的診斷準確率為90%，故障2狀態下診斷準確率為97.5%，總的診斷準確率平均值達到96.25%。

5 結語

本文根據某車型DA 462發動機實際故障現象，建立了基于振動信號分析的測試系統。對采集的信號通過Stein無偏估計的方式進行消噪，通過求取小波系數信息熵的方法得到特征向量并進行了歸一化處理；從所有樣本中合理劃分訓練集并作為輸入樣本，建立了RBF神經網絡訓練模型；并將每種工況下的20組測試樣本，輸入到訓練好的RBF神經網絡對其分類效果中進行檢驗。

通過對結果的分析，得出RBF神經網絡能夠準確、快速的進行發動機故障識別，且其故障識別準確率達96.25%。分析結果表明，在不同工況下利用信息熵提取故障特征向量，進行基于RBF神經網絡的故障診斷方法可行，對實現發動機不解體的故障診斷具有重要的應用價值。

[1]陸金銘.基于氣缸蓋振動信號的柴油機故障診斷研究[J].內燃機工程，2008，29(1)：72-76.

[2]徐玉秀，楊文平，呂軒，等.基于支持向量機的汽車發動機故障診斷研究[J].振動與沖擊，2013，32(8)：143-146.

[3]司景萍，高志鷹，梁紅波，等.基于瞬時基頻的發動機表面振動信號時域定位[J].噪聲與振動控制，2010(6)：153-[4]戴威，戴柯，郭寶圣.基于振動信號的柴油機氣閥漏氣故障診斷研究[J].煤礦機械，2007，28(15)：183-184.

[5]M Beenamol,S Prabavathy,J Mohanalin.Wavelet based seismic signal de-noising using Shannon and Tsallis entropy[J].Computers and Mathematics with Applications, 2012,64(11):3580-3593.

[6]Jamel Baili,Samer Lahouar,Mounir Hergli,et al.GPR signal de-noising by discrete wavelet transform[J].NDT&E International,2009,42(8):696-703.

[7]王拴中，朱玉田.改進小波閾值去噪法的對比性仿真實驗與分析[J].噪聲與振動控制，2012(1)，128-132.

[8]陳曉娟，王文婷，賈明超，等.基于小波熵自適應閾值的語音信號去噪新方法[J].計算機應用研究，2014，31(3)：753-755.

[9]張寧寧，王宏，付榮榮.基于小波熵的駕駛疲勞腦電信號特征提取[J].汽車工程，2013，35(12)：1139-1142.

[10]紀少波，程勇，王錫平，等.基于缸蓋振動信號頻域特征識別氣缸壓力的研究[J].振動與沖擊，2008，27(2)：133-136.

[11]黃泉水，江國，肖建昆.基于AR模型和神經網絡的柴油機故障診斷[J].振動、測試與診斷，2009，29(3)：362-365.

Engine Fault Diagnosis Based on Information Entropy and RBF Neural Network

SI Jing-ping,NIU Jia-hua,GUO Li-na,MA Ji-chang
(Inner Mongolia University of Technology,Hohhot 010051,China)

Aiming at valve clearance fault in abnormal automotive engine,a method of engine fault diagnosis without disassembly was studied with the application of information entropy of wavelet coefficients of different scales after wavelet decomposition and RBF neural network.The failure simulation test was performed on a gasoline engine.The vibration signals in cylinder head surface were measured in a normal working condition and three abnormal working conditions respectively.The collected signals were processed to eliminate the noise by Stein unbiased estimation.The characteristic vectors were extracted and normalized by using the wavelet coefficient information entropy.Then,the processed vibration signals were classified and identified by means of RBF neural network.The application example of diagnosis of the engine valve clearance faults shows that the proposed method is practical and feasible.It can be used for fault diagnosis of engines without disassembly.

vibration and wave;fault diagnosis;engine;RBF neural network;information entropy

TB53；TP206+；TK413.4；U472.42

：A

：10.3969/j.issn.1006-1335.2015.01.044

1006-1355(2015)01-0214-05+239

2014－06－25

內蒙古自然基金資助項目（2012MS0704）；內蒙古高校科研基金重點項目（NJZZ11070）

司景萍（1959－），女，呼和浩特市人，教授，主要研究方向：車輛噪聲與振動信號分析。E-mail:sip0410@sina.com

牛家驊，男，碩士生。E-mail:imut_njh1100153@sina.com