解分數百分數應用題策略十種

姜 俠

姜俠/長春市一零八學校小學部教師（吉林長春130000）。

《義務教育數學課程標準》在課程目標中明確指出“數學教學要形成解決問題的一些基本策略,體驗解決問題策略的多樣性,發展實踐能力和創新精神”.

分數、百分數應用題是小學階段應用題的重要組成部分，同時也是小學應用題的一個重點、難點．教師不僅要培養學生遇到問題會從不同方面、不同角度靈活恰當地進行分析。掌握一般的解題方法，還要掌握一些特殊的或超出一般思路以外的解題思路和解題方法，這樣不僅可以提高學生的一般解題能力，同時在某種程度上還能促進學生潛在智力、潛在能力的充分發揮．

一、分析綜合法

分析綜合法就廣泛地應用在數學解決問題中，是一種常見的一般解題方法．

例1 小明看一本120頁的連環畫，如果再看8頁，看過的頁數就相當于這本連環畫的小明看過的頁數占總頁數的幾分之幾？解法1：根據題意可知，小明再看全書的看過的頁數就是全書的所以小明看過了全書的

解法2：由條件可知，如果小明再看8頁，那么看過的頁數相當于120頁的也就是頁．所以小明實際看了48-8=40頁，由此可求出小明看過了全書的

二、假設法

“假設法”也是解決分數、百分數應用題常用的方法，就是根據所求問題的需要，先假設題中看似缺少的某個條件或某個數量存在，這樣就使題中隱蔽的數量關系凸顯出來，使原本復雜的數學問題變得更簡單，使解題思路變得更清晰．

例3 一種商品原價15元，商場搞促銷活動，降價后銷售數量增加了一半，收入增加了每件商品降價多少元？

例4 一種商品先提價10%后，又降價10%，這時該商品的價格（）．

a.與原價相同；b.高于原價；c.低于原價．

假設該商品是1元，這樣就很容易解答了：1×(1+10%)×(1-10%)＜1．所以選擇答案 c．

三、換個說法看看

有些應用題，如果按原題的題意敘述分析，題中的數量關系就不是很容易弄清．如果不改變題意而是變換個說法，常常會收到意想不到的結果，使題意豁然開朗．

例5 王紅到水果超市買了一些蘋果和桔子。交錢時，王紅把桔子單價個位上的0漏掉了，算得總價是27元，正準備付錢，售貨員說：“應該付54元才對．”請問桔子花多少錢？

“王紅把桔子單價個位上的0漏掉了”，這個條件如果換個說法，也就是王紅準備付的27元只是蘋果錢數與桔子錢數的和．而蘋果和桔子的總價為54元，兩個總錢數的差：54－27＝27（元），正是桔子錢數的所以桔子錢數為

能做到把題目中不好理解的條件換個角度去敘述，需要思維具有較強的靈活性、創造性，同時還應具有較強的概括能力．培養思維的靈活性、創造性和概括能力需要一個過程，為此，必須從低年級抓起，持續深入地訓練．下面舉例說一說改變敘述方法的訓練．

第二個已知條件的敘述可以變成下面三種說法中一種：

（1）梨樹的棵樹的2倍比桃樹多100棵；

第三個已知條件的敘述可以變成下面三種說法中一種：

（1）梨樹比杏樹多250棵；

（2）杏樹差250棵與梨樹同樣多；

（3）梨樹去掉250棵與杏樹相等．

四、轉化法

“轉化法是根據知識間的內在聯系，轉變題中條件的形式，使其本質屬性保持不變的一種思維方法”．在整數、分數、百分數應用題中“轉化法”有著廣泛的應用．

例7 某車間要加工一批零件，如果每天加工80個，需要5天完成，現在要提前1天完成，工作效率要提高百分之幾？

一般解法：[80×5÷（5-1）-80]÷80=25%．

但還可以這樣考慮，從題意中可以知道工作總量一定，這樣可以把分數應用題轉化為比例應用題．當工作總量一定時，工作時間和工作效率成反比的關系，解答方法比較簡便：[5-（5-1)]÷4=25% ．

五、尋找不變的量

有些應用題用一般方法來分析解答，往往難以找到解題思路和解題方法，這時如果抓住題目中不變的量，尋找解題的突破口，問題就會變得簡單多了．

這道題是求女員工增加的人數．但女員工人數的變化，帶來了單位1的變化，使問題變得復雜．可如果考慮到女員工雖有變化，男員工人數卻沒有變，是題中不變的量，解決問題的思路就很容易找到了．230名就對應（1－50%），又招進女員工的人數就是(280×20)÷（1-50%）-280=180(名)．

六、列表法

有些應用題，用列表的方法可以使題中的數量關系更清晰、更直觀，是解題的輔助手段，使解題的思路更容易找到。

由

七、畫圖法

由于小學生年齡較小，認知水平較低，生活經驗和知識非常有限，因此解決問題時不知從哪入手分析，尤其是分數、百分數應用題，常常讓學生束手無策．如果學生能邊讀題邊把題中的已知條件和所求問題在紙上涂一涂、畫一畫，畫出線段圖，借助線段圖進行觀察分析，就可以拓展解題思路，使題中復雜的數量關系變得直觀清晰．有利于題中數量關系明朗化,解題思路清晰化．這種解題策略，比較符合小學生善于形象思維的特點，更有利于學生找出對應量與對應分率的關系．

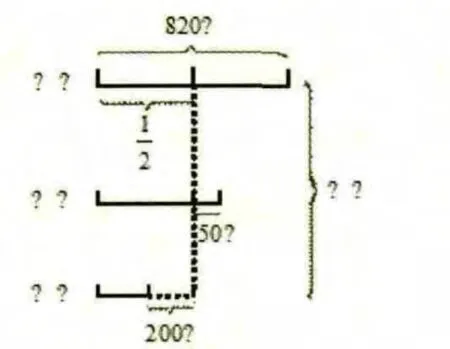
通過畫圖，可有幾種解題思路：

（1）從份數看，桃樹有2份，梨樹有3份，蘋果樹有這樣的4份，一共9份，算式略；

（2）把桃樹棵數看作單位“1”，算式略；

（3）把梨樹棵數看作單位“1”，算式略；

（4）把蘋果樹棵數看作單位“1”，算式略.

通過畫線段圖，數量關系更加明顯、直觀，使思路更加寬闊了，解題方法也多樣靈活起來.

八、還原法

有些數學問題的解答，需要從所求問題最后的結果出發，利用加法與減法、乘法與除法的互逆關系，根據已知條件從后往前一步一步地倒著推算，使問題得到解決.

例11 某服裝廠要加工一批服裝，第一周加工了全部的40%，第二周加工了余下的還有900件沒有加工，這批服裝一共有多少件？

例12 一個最簡分數，分子、分母的和是50，如果分子分母都減去5，所得的分數是2/3，求這個分數原來是多少？

根據分子、分母都減去5這個條件，可以求出現在分子和分母的和，即50-2×5，得到現在的和40后，明顯發現2/3的分子、分母的和比40小，說明已經約分了，可以用所得的和40除以2+3的和，即得到分子、分母同時除以的那個數，再用這個數分別乘2乘3，就得到原分子、分母減去5后的分子和分母，然后再分別加上5，就得到了原來的分數.即50-2×5=40，40÷（2+3）=8，2×8+5=21，3×8+5=29 原分數是 21/29.

九、用份數解應用題

例13 某車間計劃用42天加工一批零件，計劃平均每天加工120個，實際比計劃每天多加工，實際用多少天加工完？

如果用份數思考，原計劃平均每天完成1份，42天共42份，實際每天完成份，要求實際用多少天完成，就看42份中包含幾個36（天）.

十、應用正、反比例解題

有些分數、百分數應用題，若用一般方法求解，思路既復雜、計算也麻煩，如果用正、反比例的知識求解，就顯得十分簡單了.

例14 某服裝廠要生產1200件服裝，加工3天，完成40%，照這樣計算，完成全部任務一共需多少天？

一般解法：先求得前3天生產服裝的件數1200×40%=480（件），再求得每天生產的件數480÷3=160（件），最后求總得天數 1200÷160=7.5(天）.

應用比例知識：根據題意，工作效率一定，工作時間與工作量成正比例，比例式：總件數/共需天數=已生產的件數/已生產的天數，也可寫成：已生產的天數/共需天數=已生產的件數/總件數=40%，根據此式可得：3/共需天數=40%，很容易求出共需用的天數為3÷40%=7.5（天）.

例15 一個修路隊要修一段公路，計劃每天修3.2千米，實際每天比原計劃多修25%，實際用了12天修完，原計劃用多少天？

一般解法：先求實際每天修的千米數，再求這段公路的總長，最后求原計劃用的天數，列式為：3.2×（1+25%）×12÷3.2=15（天）.

根據要修的公路長一定，工作效率與工作時間成反比例，列出的比例式：原計劃每天修的千米數×原計劃的天數=實際每天修的千米數×實際的天數，也可寫成：原計劃的天數/實際的天數=實際每天修的千米數/原計劃每天修的千米數=1+25%，可得，原計劃的天數/12=1+25%，從而很快求得原計劃的天數：12×（1+25%）=15（天）.

不難看出，有些可用比例知識解答的分數、百分數應用題，解答時，可根據題意先寫出文字的等式，再根據題意作適當轉換，問題就很容易解答了。

著名教育家米山國藏指出：“學生所學的數學知識，在進入社會后幾乎沒有什么機會應用，因而這種作為知識的數學，通常在走出校門后不到一兩年就忘掉了.然而不管他們從事什么工作，唯有深深銘刻于頭腦中的數學思想和方法等隨時地發生作用，使他們受益終身.”面對紛繁復雜的數學問題能多角度、多層面、多策略地去分析把握問題的實質，視野就會更開闊，思維的素養也會更提升，同時能深刻領悟其背后所蘊含的數學思想.