談談如何提高數(shù)學知識的記憶力

蘇順修

（濰坊工商職業(yè)學院，山東 諸城 262200）

學習的過程是不斷積累知識和增強能力的過程，而知識的積累是靠記憶來完成的，記憶力學生必須具備的基本能力之一，也是學習的基礎條件。那么如何根據(jù)數(shù)學的特點和規(guī)律，在教學工作中培養(yǎng)和提高學生的記憶力？筆者將介紹幾種自己在工作實踐中總結出的方法。

1 目標記憶

記憶要有的放矢，尤其是在學習數(shù)學知識時，首先要明確學習的具體任務，清楚記憶的長遠目標，做到心中有數(shù)，這樣就有了記憶的興趣和動力，從而產(chǎn)生了記憶的決心和信心，也就將知識記住了。

縱觀變換紛繁的數(shù)學試題，基本上都源于教材重點，凡是大綱中要求熟練掌握和靈活運用的內(nèi)容都是學習的重點，也是高考的重點，往年的高考試題就體現(xiàn)了這一點。如1999年高職考試試題：已知三棱錐D-ABC 的三個側面與底面全等，且AB＝AC＝√3，BC＝2，則以BC 為棱，以BCD 為面的兩面角的大小是A）л/3，B)л/4，C)л/2，D)2л/3.若考生熟悉三棱錐的做圖法、兩面角的平面角概念，再做一些簡單的推理和計算，就可以迅速得出本題的答案為C)。

2 理解記憶

理解是記憶的基礎，對學習數(shù)學知識來說更是如此。思維、理解對記憶有著巨大的作用，對所學的知識，只有經(jīng)過思維的錘煉，才能徹底理解，也才能牢固地記憶和靈活地運用，所謂理解就是找出事物變化的規(guī)律、事物之間的聯(lián)系，把新舊知識融合起來，才能建立多方面的聯(lián)系，才能拓寬知識面、思維空間和知識的應用范圍，也才能記得牢、用的活。所以，在數(shù)學知識的學習過程中，要不斷開拓思維和培養(yǎng)思維的邏輯性、獨立性、靈活性，只有養(yǎng)成獨立思考的習慣，做到深刻地理解教材，才能在理解的基礎上，牢固掌握知識，靈活運用知識，才能實現(xiàn)由已知到未知的推理記憶。例如，等差數(shù)列前n 項和的公式：Sn＝n(a1+an)/2，只要掌握了“距首末兩項距離的和相等”的性質(zhì)，就能很容易在理解的基礎上記住這個公式。再如，等差數(shù)列的通項公式：an＝a1+(n-1)d.只要理解了等差數(shù)列的實質(zhì)是“后一項與前一項的差為常數(shù)d”，就很容易記住了。

3 反復閱讀與嘗試回憶相結合記憶

重復是記憶之母，在數(shù)學學習中，新掌握的知識，若不及時反復閱讀和推導，初試印象就會逐漸淡化消失。因此，當天所學的知識，課后要及時整理，反復閱讀推導，強化記憶。同時，還應做嘗試回憶，檢驗記憶效果和進一步鞏固記憶，對那些還沒有達到記憶效果的知識，要及時補充閱讀和深化理解，直到達到記憶效果為止。如在學習三角中的兩角和與差的三角公式、倍角與半角公式、萬能公式時，一是要分析公式特點，并在課后演練推導；二是每天要抽出幾分鐘時間默寫公式，逐步養(yǎng)成這種自我檢查的良好習慣，提高正確再認與回憶能力，就能夠達到良好的記憶效果。

4 系統(tǒng)化記憶

事實證明，經(jīng)過思維加工的系統(tǒng)化的知識具有邏輯性強、層次分明、井井有條的特點，能較長時間地保存在頭腦中，且易于提取。所以，在數(shù)學的學習中，要不斷提高對知識的組織能力、邏輯推理能力和歸納能力，對復雜的知識要寫要點、排順序、編口訣、圖上作業(yè)、構造“公式”等，將需要記憶的知識系統(tǒng)化，做到綱舉目張，從整體上達到記憶效果。如數(shù)學中的“母概念”與“子概念”、“母公式”與“子公式”等，可設計樹形結構圖或公式繁衍圖等來加強記憶。例如，三角中的誘導公式，有6 種函數(shù)9 種角的情況，共推出54個公式，如果獨立地記憶是很困難的，為方便記憶，可將這54個誘導公式濃縮為如下形式：

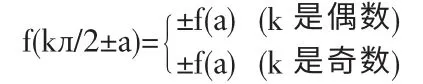
其中，f(а)表示6 種三角函數(shù)中的任一種函數(shù)，f(а)表示f(а)的余函數(shù)，即(kл/2±а)的各三角函數(shù)值。當k 是偶數(shù)時，等于а 的同名三角函數(shù)值；當k 是奇數(shù)時，等于а 的相應函數(shù)的余函數(shù)值，然后加上把а 看作銳角時角(kл/2±а)的原函數(shù)所在象限的符號，最后進一步概括為“單變雙不變，符號看象限”，就更容易記憶，且記憶效果更好。

5 聯(lián)想發(fā)展記憶

記憶是建立在事物之間相聯(lián)系的橋梁，實踐證明，對知識認識的過程是“溫故知新”和“知新溫故”的對立統(tǒng)一的過程。即已學過的知識是一切后來要學習知識的基礎。舊知識積累越多，新知識聯(lián)系的就越廣，就越容易產(chǎn)生聯(lián)想，越容易理解新知識、記住新知識。例如，要記住四面體的某些性質(zhì)，可聯(lián)想三角形的某些性質(zhì)，因為四面體在空間圖形中的地位，類似于三角形在平面圖形中的地位，因此，可根據(jù)三角形的性質(zhì)記憶四面體的性質(zhì)。又如，扇形面積S＝1/2lr 和圓錐側面積S側面＝1/2lr 這兩個公式是學生容易記住的，因為這兩個公式的記憶可聯(lián)系三角形面積公式。從而可以看出，諸如把空間問題與平面問題基于結構相似而進行聯(lián)想記憶，是提高記憶效率、發(fā)展記憶力的有效途徑之一。

6 數(shù)形結合記憶

直觀圖像是有力的記憶助手。實驗證明，經(jīng)常有意識地記憶圖像、回憶圖像，以形成和喚起表象，有利于記憶抽象的數(shù)學知識，有利于提高解題速度和解題的正確性。例如，記憶對數(shù)函數(shù)10gax(a﹥0 且a≠1)的性質(zhì)，只要形成函數(shù)圖像的表象，就能順利地描述函數(shù)的性質(zhì)，且能運用性質(zhì)順利地解決數(shù)學問題。因此，可以發(fā)揮圖形的作用，增強記憶效果。

總之，記憶必須以“運用”來強化，即一方面通過實踐把知識固定在記憶里，另一方面直接接觸事物，在可能的范圍內(nèi)，盡量通過感觀去進行，這就要求學生必須把自己的多種感覺通過大腦進行立體加工，這樣可以培養(yǎng)學生的良好記憶品質(zhì)，迅速提高記憶力。