“知道者悖論”解析

張 瑩，雒自新

(1.西安電子科技大學外國語學院，西安 710071;2.西安交通大學人文社會科學學院，西安 710049)

悖論問題是困擾人類心智千年的難題。有的哲學家甚至認為整個一部哲學史可以看作是與各種悖論做斗爭的歷史。在為數眾多的悖論當中最著名當數說謊者悖論，這不僅因為它具有十分悠久的歷史，更是因為該悖論以最為簡單的形式告訴人們，通常對“真”這一我們日常生活中普遍使用的概念的直覺理解是包含矛盾的。考慮語句(L):L是假的。那么L這句話是真的還是假的呢?如果L為真，那么它說的是自己為假，因而它為假;如果L為假，那么說它自身為假是假的，因此它又為真。這顯然是矛盾的，但我們又找不出問題究竟出在哪里。語句L被稱為“說謊者語句”，“說謊者悖論”這一名稱由此而來。

對說謊者悖論的探討已經持續了兩千多年，但遺憾的是至今仍沒有就該悖論的解決意見達成一致。值得注意的是進入20世紀中后期以來，一類型新的悖論走進了研究者們的視線，并逐漸得到了邏輯學家與哲學家們的重視，這就是知道者悖論。在持續多年的研究過程中，該悖論多層面的理論意義與學術價值逐步得以彰顯［1］。與說謊者悖論類似，知道者悖論當中也涉及類似的語句，即所謂知道者語句(K):認知主體i知道K為假，該悖論由此而得名。然而，許多學者對“知道者悖論”(Knower Paradox)這一概念所指稱的對象卻并不清楚，甚至與其簡化形式或者其前身——絞刑悖論——相混淆。另外，在道義邏輯中也有所謂知道者悖論。因此，澄清“知道者悖論”這一概念就顯得非常必要。

一、知道者悖論的前身

知道者悖論的起源可以追溯到20世紀40年代在歐洲民間流傳的“突然演習問題”。在持續多年的研究中，“突然演習問題”逐漸演變為一個著名的哲學問題——“絞刑悖論”。也就是說，知道者悖論來源于其前身——絞刑悖論，但與該前身卻并不完全相同。

絞刑悖論描述的是如下場景:法官向一名罪犯宣判，他被判處絞刑，而且該罪犯將在從宣判之日的第二天起的10天中的某一天被執行絞刑，但這次絞刑是一次令罪犯出乎意料的絞刑，意思是說，在執行絞刑的前一天晚上，罪犯不會知道絞刑將在第二天執行。這看似一則很正常的宣判，然而當這名聰明的罪犯聽到該宣判時，心中一陣竊喜:按照該宣判，自己不會被執行絞刑。為什么呢?該罪犯的如意算盤是這樣的:根據法官的宣判，絞刑不可能在這10天中的最后一天執行，這是因為如果在最后一天執行，那么由于前9天都沒有執行絞刑，所以在倒數第二天(也就是第9天)晚上，我就會知道第二天(也就是最后一天)將執行絞刑，但這不滿足法官所宣判的這次絞刑的“意外性”，因而絞刑不可能在最后一天執行。絞刑也不可能在倒數第二天執行，因為如果在倒數第二天執行，那么由于前8天都沒有執行絞刑，而前面的推理已經排除了絞刑在最后一天執行的可能性，所以在倒數第三天(也就是第8天)晚上，我就會知道第二天(也就是倒數第二天)將執行絞刑，這再一次不滿足法官所宣判的絞刑的“意外性”，因而絞刑不可能在倒數第二天執行。按照同樣的思路進行推理，可以依次排除絞刑在倒數第三天、倒數第四天……執行。于是該罪犯斷定法官的宣判是不可實現的。然而，法官就在接下來的第四天突然來到該罪犯面前對他執行了絞刑，這大大出乎該罪犯的意料，從而不折不扣地實現了之前的宣判。可悲的是，該罪犯到死都沒有明白為什么自己無懈可擊的推理當中卻包含著矛盾。

前面，我們以非形式的方式敘述了絞刑悖論。盡管該悖論還有諸多實質相同的其他版本，比如克里普克(S.A Kripke)［2］寧愿稱之為“意外考試悖論”，但我們還是遵循蒯因(W.V.Quine)的稱謂將之稱為“絞刑悖論”。經過奧康納(D.O’Connor)［3］、斯克利文(M.Scriven)［4］、蒯因［5］、沙烏(R.Shaw)［6］、蒙塔古(R.Montague)和卡普蘭(D.Kaplan)等哲學家與邏輯學家的深入研究與整理，前述非形式敘述的絞刑悖論已經發展成一個關于“知識”概念的嚴格的自指悖論。

從前述非形式敘述不難看出，絞刑悖論中絞刑不可能執行的推導與天數無關。因此，在這里為簡潔明了起見，只考慮有兩個可選擇日子的情形，這不會影響問題的實質。如果用p代表罪犯，F代表“絞刑發生在第一天”，S代表“絞刑發生在第二天”，f表示第一天，z表示宣判的當天，A代表法官的判決。Ki(x)解釋為“認知主體i知道x”。符號I(s，t)是一種縮寫，它表示“從s可以合乎邏輯地推導出t”。則法官的宣判的嚴格形式如下(其中(「﹁A?表示語句﹁A的標準名稱的哥德爾數):

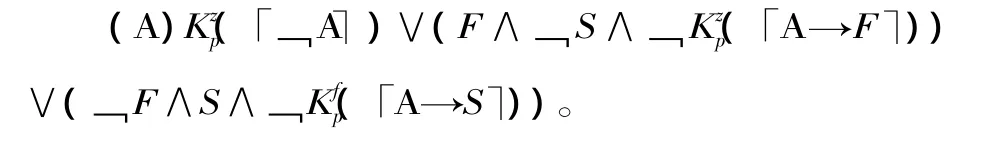
絞刑悖論所描述的情境(也就是推導出矛盾所使用的前提)的嚴格形式如下:

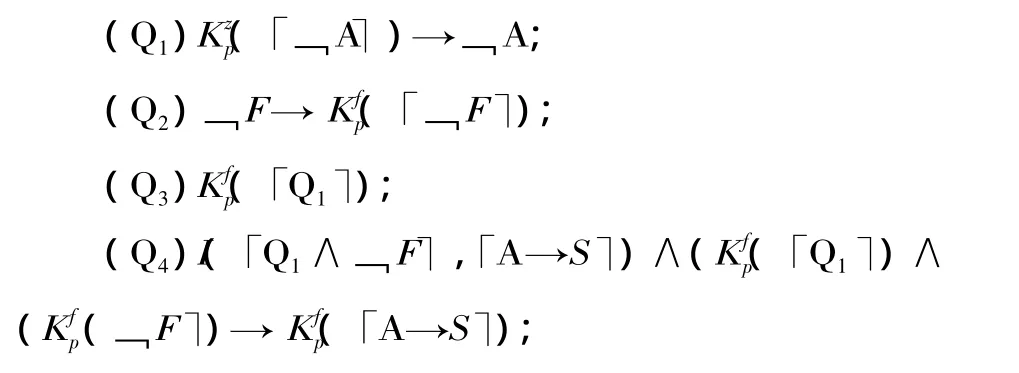
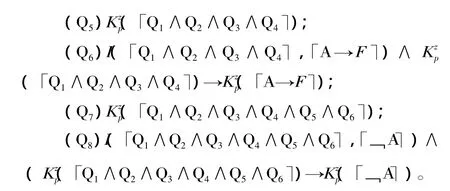
在以上8條前提中，Q1表示“如果罪犯在宣判之日知道﹁A，那么﹁A為真”，即“知識蘊含真理”原則，這是最基本的認知規則。Q4、Q6與Q8表達的則是知識的演繹封閉性。Q2、Q3、Q5與Q7表達罪犯作為正常的具有起碼理性的認知主體所具有的基本認知與記憶能力，例如Q2表示“如果絞刑在第一天沒有執行，那么罪犯在第一天知道這一點”。

法官的宣判A可以經由哥德爾自指定理在擴充的形式算術系統當中得到表達，即是擴充的形式算術系統當中的一條定理。在形式算術系統當中經過嚴格的邏輯推理，既可以推出A，即宣判必定能實現;又可以推出﹁A，即宣判不能實現(具體推導過程詳見參考文獻［7］，本文限于篇幅略去)。于是，矛盾就產生了。

矛盾的產生表明，Q1～Q8這組前提假設與“初等語法”(即形式算術)原則是不相容的。也就是說，如果我承認這組前提假設是合理的，并且與此同時也承認“初等語法”的合理性，那么一個貨真價實的邏輯悖論就產生了。這就是知道者悖論的前身——絞刑悖論。這個悖論的重要性恰恰“來自于這些假定的直覺合理性。無疑地，在發現這個悖論之前，人們也肯定會有把體現在Q1～Q8中的認識論原則充分形式化的要求，這即使不是必需的，至少不是不可能的”［7］89。

二、知道者悖論的嚴格刻畫

前述絞刑悖論嚴格的形式刻畫是由蒙塔古和卡普蘭在其1960年發表的文章中給出的［7］，他們認為該悖論的出現必將會引出哲學認識論上的某些新探討，因此他們在給出這種刻畫之后，對該問題進行了進一步深入的思考。蒙塔古和卡普蘭發現，可以考慮一個從該悖論引申出來的更簡單的結果，這樣就會使問題變得更加尖銳。如前所述，絞刑悖論中絞刑不可能執行的推導與天數無關。也就是說，即使只考慮一個而不是兩個可能的執行絞刑日期，仍然可以得到一個嚴格的悖論。在這種情形下法官的宣判為如下形式:“除非罪犯在宣判之日晚上知道本宣判為假，否則下述要求將被滿足:絞刑在接下來的一天執行，而罪犯在宣判之日晚上不知道基于本宣判‘絞刑在接下來的一天執行’為真。”

實際上，可以沿著這條思路繼續進行下去，執行絞刑的可能日期的數目可以進一步縮減至零。此時法官的“宣判”只是斷言下面這個唯一的要求將被滿足:“罪犯在宣判之日晚上知道本宣判為假。”該“宣判”可以用如下公式表達:

在皮亞諾算術系統(或者與之等價的魯濱遜算術系統)當中引入一個一元謂詞Ki(x)(對該謂詞的解釋如前)，并且引入與Q1、Q3和Q4類似的表達認識論規律的一般規則作為定理:

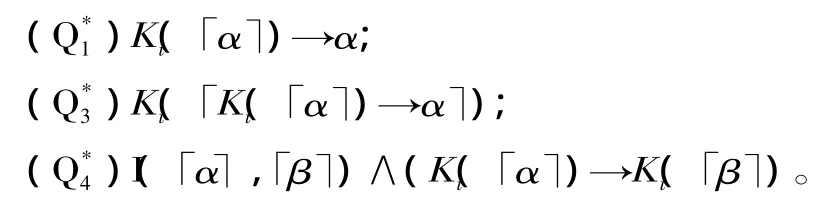
由哥德爾自指定理得，下述表達法官的宣判的公式是該形式系統中的定理:

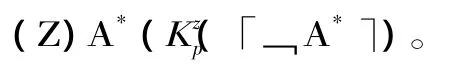
由此所得到的系統記作T，在T中可作如下演繹推導:

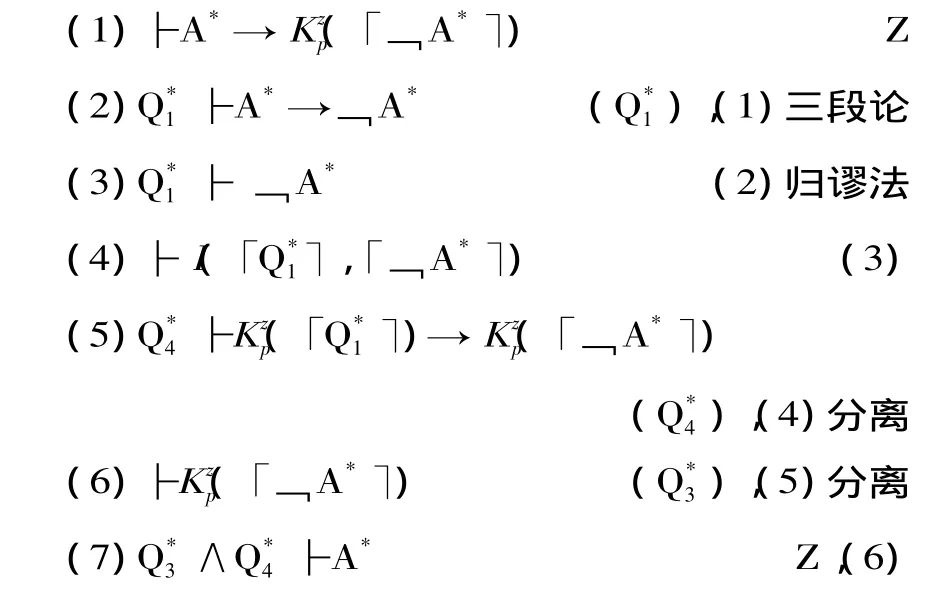
在上述推導當中，式(3)得到了﹁A*，而(7)得到了A*，這顯然是矛盾的。語句A*是說，其自身的否定為認知主體p所知道。這與著名的說謊者語句(即“本語句為假”)的形式十分類似，因而可以將語句A*稱為“知道者語句”。

三、簡化的知道者悖論

在多年的研究當中，知道者悖論有時候也以它的簡化形式出現。從以上知道者悖論的嚴格形式刻畫的過程中不難看出，哥德爾自指定理起到了至關重要的作用，因為該定理使得法官的宣判這一自指語句經符號表達之后成為形式算術系統的一條定理。稍加分析可知，由哥德爾自指定理所得，與前述(Z)類似的同樣是皮亞諾算術系統或者魯濱遜算術系統的定理。在以上解釋之下，語句A＊＊的意思是:認知主體p不知道A＊＊。相比之下，語句A＊＊在結構上比前面的語句A*更接近于“說謊者語句”L:L?﹁T(「L?)。如果把知道者語句構造為A＊＊，則稍加修改認知規則以及推導建構所依賴的形式系統，就可以構造出知道者悖論的另一個簡化版本(相應地，前面提到的可以稱之為知道者悖論的經典版本)。

同理，在皮亞諾算術系統或者魯濱遜算術系統中添加一個被解釋為“認知主體i知道哥德爾數為x的語句”的一元謂詞Ki(x)。把如下表達認知規則的公式和推理規則分別作為公理和推導規則引入該系統:

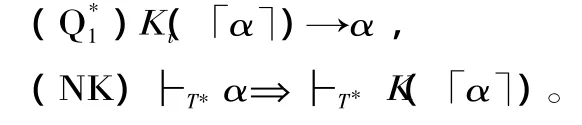
由此所得到的系統記作T*，在T*中可作如下演繹推導:

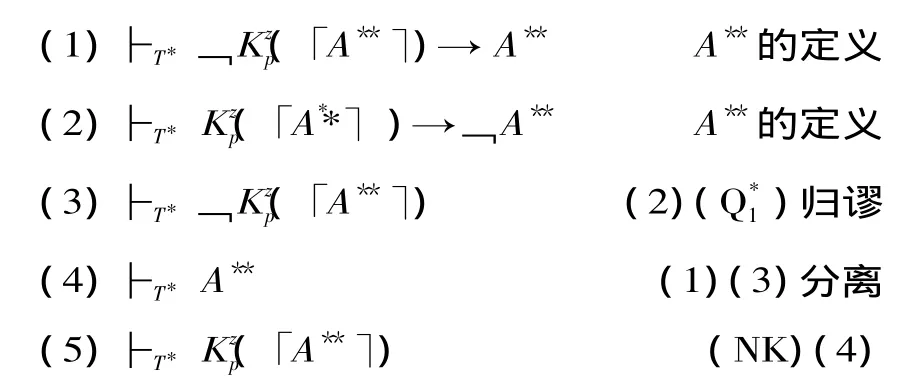
顯然，式(3)和(5)矛盾，于是悖論得以建構。在許多對知道者悖論的研究文獻當中，所針對的實際上是知道者悖論的該簡化形式，可以稱之為“簡化的知道者悖論”。

四、道義邏輯中的知道者悖論

值得注意的是，在相關文獻中還有一類所謂的“知道者悖論”——“道義邏輯中的知道者悖論”(the paradox knower in deontic logic)。所謂“道義邏輯”(Denotic Logic)也稱規范邏輯，是研究“應該”“允許”“禁止”等概念的廣義模態邏輯的分支之一。道義邏輯中的知道者悖論如下，考察下面 3 個語句［8］:

(I)在趙六看守倉庫期間王五在倉庫放火。

(II)如果在趙六看守倉庫期間王五在倉庫放火，那么趙六應該知道這件事。

(III)王五不應該在倉庫放火。

這3個語句看起來都很正常，并沒有什么特別之處，而且我們也能夠理解它們的意思。然而，如果以它們為前提，再加上如下兩條規則，就可以推導出矛盾:

(D)被應該的東西蘊含的東西也是應該的。

(V)趙六知道王五在倉庫防火“蘊含”王五在倉庫放火。

由(IV)、(V)和規則(D)得:

(VI)王五應該在倉庫放火。

這樣，(III)和(VI)矛盾。

矛盾的導出所依賴的前提包括:表達事實的語句(I)、符合直覺的道義語句(II)和(III)、基本道義規則“被應該的東西所蘊含的東西也是應該的”、認知規則，以及經典邏輯中的分離規則。這些前提均為具有“道義思維”的認知共同體所普遍接受。這就是所謂“道義邏輯中的知道者悖論”。從以上推導過程不難看出，如果沒有認知規則，就得不出(V)，而若沒有(V)就無法應用道義規則(D)，也就不可能得到(VI)。也就是說在這里的矛盾的導出中起到了至關重要的作用，“道義邏輯中的知道者悖論”由此而得名。

五、結論

知道者悖論是關于“知道”的嚴格意義的邏輯悖論。所謂嚴格意義的邏輯悖論“指謂這樣一種理論事實或狀況，在某些公認正確的背景知識之下，可以合乎邏輯地建立兩個矛盾語句相互推出的矛盾等價式”［9］。由于該悖論以最為簡單的形式告訴人們，通常對“知道”這一概念的理解是包含矛盾的，所以知道者悖論得到了來自任何關注知識概念的學科的廣泛重視。尤其是進入21世紀以來，知道者悖論研究取得了迅速發展［10］。

與經典版本相比，在簡化的知道者悖論當中，矛盾的導出并沒有用到認知規則而是代之以推理規則(NK)。但顯然，在系統T*中，從公理和(NK)出發可以推導出和

在道義邏輯中的知道者悖論當中，矛盾的導出本質地涉及到了認知規則(Q*1)，因而與知道者悖論及其簡化形式與前身有著十分密切的聯系。但很顯然，兩者之間也存在著本質上的不同:道義邏輯中的知道者悖論還本質地涉及到了基本道義規則，因而是一個比知道者悖論更為復雜的問題。

綜上所述，在不同的情境當中，由于背景知識的不同，“知道者悖論”(Knower Paradox)這一概念與4個悖論相關。因此，對知道者悖論進行研究，首先應該明確這4個悖論之間的聯系與區別。

［1］雒自新.知道者悖論及其價值［J］.科學技術哲學研究，2010(4):46-49.

［2］Kripke S A.On Two Paradoxes of Knowledge［C］//Philosophical Troubles:Collected Papers.Oxford:Oxford U-niversity Press，2011:27.

［3］O’Connor D.Pragmatic Paradoxes［J］.Mind，1948(57):358-359.

［4］Scriven M.Paradoxical Announcement［J］.Mind，1951(60):403-407.

［5］Quine W V.On a So-Called Paradox［J］.Mind，1953(62):65-67.

［6］Shaw R.The Paradox of the Unexpected Examination［J］.Mind，1958(67):382-384.

［7］Montague R，Kaplan D.A Paradox Regained［J］.Notre Dame Journal of Formal Logic，1960(1):79-87.

［8］Feldman F.The Paradox of the Knower［J］.Philosophical Studies，1989(55):93-100.

［9］張建軍.邏輯悖論研究引論:修訂［M］.北京:人民出版社，2014:7.

［10］雒自新.“知道者悖論”研究新進展述評［J］.哲學動態，2009(7):81-85.