多軸隨機(jī)振動(dòng)試驗(yàn)控制技術(shù)研究

邱漢平，馮咬齊,2，樊世超

（1.北京衛(wèi)星環(huán)境工程研究所，北京 100094； 2.北京衛(wèi)星環(huán)境工程研究所 可靠性與環(huán)境工程技術(shù)重點(diǎn)實(shí)驗(yàn)室，北京 100094）

0 引言

在振動(dòng)環(huán)境模擬試驗(yàn)領(lǐng)域，相對(duì)于單軸激勵(lì)振動(dòng)方式，多軸振動(dòng)激勵(lì)能更真實(shí)地模擬實(shí)際的動(dòng)力學(xué)環(huán)境，從而可暴露大型復(fù)雜結(jié)構(gòu)在單軸振動(dòng)激勵(lì)時(shí)不易被發(fā)現(xiàn)的缺陷。多軸振動(dòng)試驗(yàn)技術(shù)自20世紀(jì)60～70年代出現(xiàn)以來(lái)，其應(yīng)用由初期的地震、汽車、軍工等行業(yè)逐漸擴(kuò)展到航空、航天領(lǐng)域[1-4]。在多軸隨機(jī)振動(dòng)試驗(yàn)技術(shù)中，多軸振動(dòng)控制既是試驗(yàn)的關(guān)鍵點(diǎn)，也是試驗(yàn)的一個(gè)難點(diǎn)。國(guó)外開(kāi)展了大量的多軸振動(dòng)控制技術(shù)研究，并推出了如Spectral Dynamics 公司的Jaguar 及Data Physics 公司的Signal Matrix 等多軸控制軟件產(chǎn)品[5]。相比之下，國(guó)內(nèi)卻還沒(méi)有成熟的商用產(chǎn)品問(wèn)世。通過(guò)學(xué)習(xí)和借鑒國(guó)外的多軸控制技術(shù)，北京衛(wèi)星環(huán)境工程研究所自主研發(fā)了一套多軸隨機(jī)振動(dòng)控制系統(tǒng)。

本文在介紹多軸隨機(jī)振動(dòng)控制基本原理的基礎(chǔ)上，詳細(xì)分析利用自主研發(fā)的控制系統(tǒng)在三軸振動(dòng)試驗(yàn)臺(tái)上進(jìn)行三軸隨機(jī)振動(dòng)試驗(yàn)的控制效果。開(kāi)展多軸振動(dòng)試驗(yàn)控制技術(shù)研究將為深入認(rèn)識(shí)多軸振動(dòng)模擬試驗(yàn)機(jī)理、分析研究和制定多軸振動(dòng)試驗(yàn)條件等方面提供參考。

1 多軸隨機(jī)振動(dòng)控制原理

1.1 系統(tǒng)傳遞特性辨識(shí)

多軸振動(dòng)試驗(yàn)系統(tǒng)可以描述成如圖1所示的多輸入多輸出系統(tǒng)。

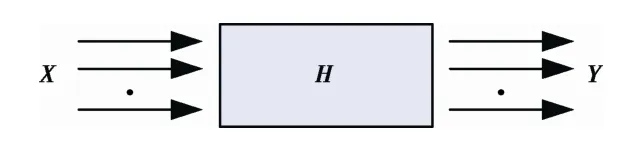
圖1 多軸振動(dòng)試驗(yàn)系統(tǒng)模型示意 Fig.1 Schematic diagram of the model of the multi-axis vibration test system

其中，辨識(shí)系統(tǒng)的傳遞函數(shù)是多軸隨機(jī)振動(dòng)試驗(yàn)控制的關(guān)鍵環(huán)節(jié)。多軸振動(dòng)試驗(yàn)系統(tǒng)同時(shí)輸入N路低量級(jí)的獨(dú)立隨機(jī)驅(qū)動(dòng)信號(hào)并測(cè)量系統(tǒng)在N個(gè)控制點(diǎn)上的響應(yīng)輸出信號(hào)。假定多軸振動(dòng)試驗(yàn)系統(tǒng)是線性時(shí)不變系統(tǒng)，則系統(tǒng)的輸入輸出信號(hào)在頻域內(nèi)可表達(dá)為

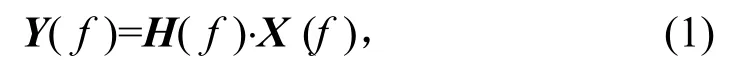
式中：Y(f)為N維系統(tǒng)響應(yīng)矢量；H(f)為N×N維系統(tǒng)傳遞函數(shù)矩陣；X(f)為N維驅(qū)動(dòng)信號(hào)矢量。將式(1)兩邊同時(shí)乘以驅(qū)動(dòng)信號(hào)矢量的共軛轉(zhuǎn)置，則有

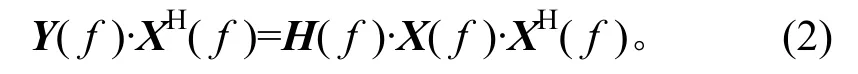
令SYX(f)=Y(f)·XH(f)，SXX(f)=X(f)·XH(f)，則式(2)可簡(jiǎn)化為

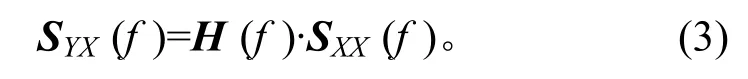
式(3)兩邊同時(shí)乘驅(qū)動(dòng)自譜逆矩陣，則可得系統(tǒng)傳遞函數(shù)為

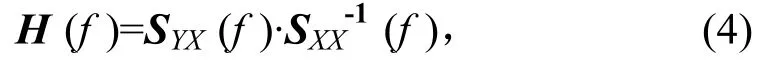
其中響應(yīng)與驅(qū)動(dòng)互譜矩陣SYX(f)及驅(qū)動(dòng)自譜矩陣SXX(f)展開(kāi)后表示為

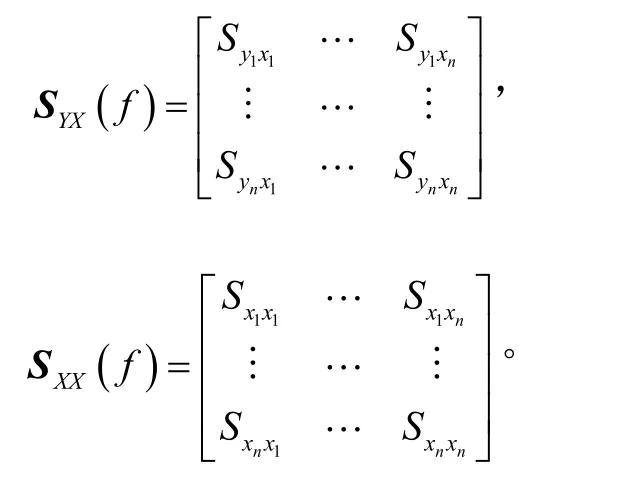
對(duì)于系統(tǒng)在某些頻率點(diǎn)處出現(xiàn)奇異或系統(tǒng)為非方陣控制時(shí)，頻響函數(shù)矩陣辨識(shí)可用Moore- Penrose 求偽逆的方法進(jìn)行。

1.2 驅(qū)動(dòng)信號(hào)生成

多軸隨機(jī)振動(dòng)控制驅(qū)動(dòng)信號(hào)生成方法可以按圖2方式進(jìn)行。

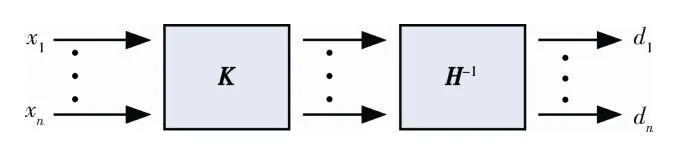
圖2 驅(qū)動(dòng)信號(hào)生成示意 Fig.2 Schematic diagram of the drive signal generation

圖2中，x1,x2,…,xn為獨(dú)立的白噪聲信號(hào)，其功率譜密度矩陣為單位矩陣。即設(shè)X(f)=[x1(f)，x2(f),…,xn(f)]T，白噪聲功率譜密度矩陣為Xwn(f)，則有

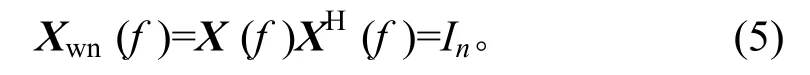
矩陣K(f)為一個(gè)下三角矩陣，它通過(guò)對(duì)正定參考譜矩陣進(jìn)行Cholesky 分解而得到，則有

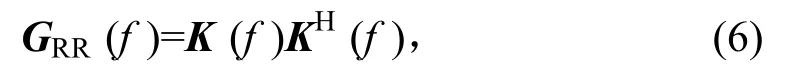
式中：KH(f)矩陣為分解矩陣K(f)的共軛轉(zhuǎn)置。

設(shè)H-1(f)為多軸試驗(yàn)系統(tǒng)的傳遞函數(shù)矩陣的逆矩陣，根據(jù)圖2，可以得出初始驅(qū)動(dòng)信號(hào)的頻域序列，

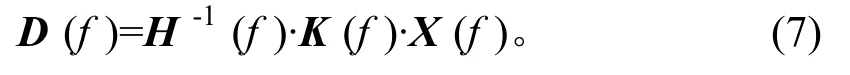
1.3 控制算法

在多軸隨機(jī)振動(dòng)試驗(yàn)過(guò)程中，由于試驗(yàn)系統(tǒng)噪聲、非線性等因素的影響，使得控制系統(tǒng)無(wú)法非常準(zhǔn)確地估計(jì)系統(tǒng)的頻響函數(shù)矩陣，從而使獲取的系統(tǒng)響應(yīng)頻譜矩陣與參考譜矩陣之間存在偏差。因此，在試驗(yàn)過(guò)程中需要對(duì)驅(qū)動(dòng)信號(hào)進(jìn)行實(shí)時(shí)的修正，以確保響應(yīng)譜矩陣在容差范圍內(nèi)。

試驗(yàn)過(guò)程中驅(qū)動(dòng)信號(hào)的修正主要通過(guò)更新多軸隨機(jī)振動(dòng)控制K(f)矩陣來(lái)實(shí)現(xiàn)[6-10]，K(f)矩陣修正流程見(jiàn)圖3。其中：x為白噪聲信號(hào)矢量；Kold為待更新的K(f)矩陣；Δ為修正的誤差矩陣；H為系統(tǒng)真實(shí)的傳遞函數(shù)矩陣；為實(shí)測(cè)傳遞函數(shù)矩陣的逆矩陣；c為系統(tǒng)的響應(yīng)矢量。

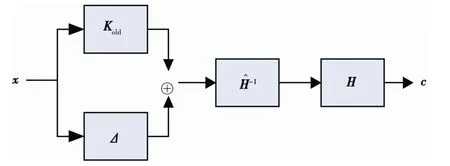
圖3 多軸隨機(jī)控制K 矩陣修正圖 Fig.3 The correction of matrix K in the multi-axis random vibration control

在K(f)矩陣修正之前，有

響應(yīng)譜密度矩陣為

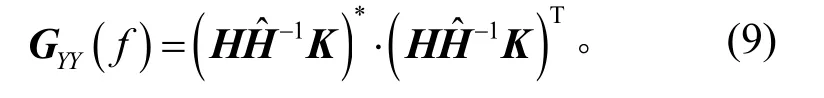
經(jīng)過(guò)修正之后，響應(yīng)互譜密度矩陣應(yīng)該等于理想的參考譜密度矩陣GRR(f)，即

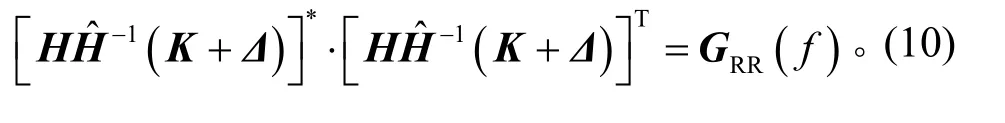
聯(lián)立式(9)、式(10)并展開(kāi)，得

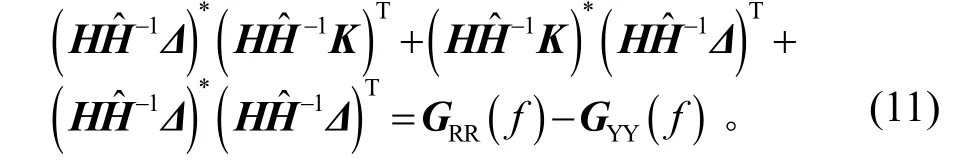
由于系統(tǒng)噪聲及非線性等影響，系統(tǒng)的頻響函數(shù)估計(jì)與真實(shí)的頻響函數(shù)有偏差，即

式中：Ⅰ為單位矩陣；E為小誤差矩陣。因而有

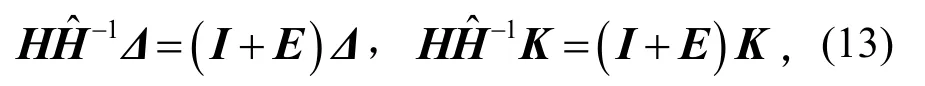
忽略EΔ,EK兩矩陣小量，則式(13)可分別簡(jiǎn)化為

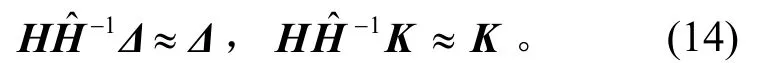
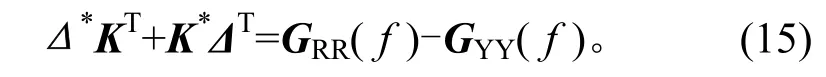
為確保多軸隨機(jī)控制收斂，每一次閉環(huán)只能將誤差的一部分用來(lái)修正，即需引入一收斂因子ε。因此控制修正算法的最終表達(dá)式為

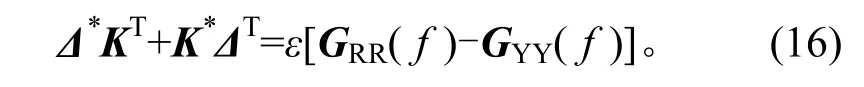
根據(jù)公式(16)求解誤差矩陣Δ后，系統(tǒng)的K(f)矩陣可通過(guò)式(17)進(jìn)行修正和更新，

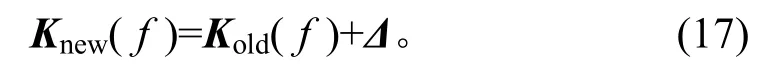
多軸隨機(jī)振動(dòng)控制算法流程見(jiàn)圖4。

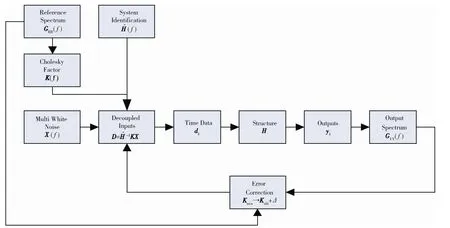
圖4 多軸隨機(jī)振動(dòng)控制算法流程 Fig.4 The flow chart of the multi-axis random vibration control algorithm

2 控制系統(tǒng)及控制試驗(yàn)驗(yàn)證

2.1 振動(dòng)臺(tái)系統(tǒng)

三軸振動(dòng)試驗(yàn)系統(tǒng)由3 個(gè)振動(dòng)臺(tái)、液壓球頭、工作臺(tái)面、功率放大器、風(fēng)機(jī)、液壓油泵以及多軸振動(dòng)控制系統(tǒng)等組成。三軸振動(dòng)試驗(yàn)臺(tái)見(jiàn)圖5。單個(gè)振動(dòng)臺(tái)的額定推力為6 kN，球頭的最大橫向位移為40 mm，相對(duì)角位移為±6°，工作頻率為5～2000 Hz。

圖5 三軸振動(dòng)試驗(yàn)系統(tǒng) Fig.5 The triaxial vibration test system

2.2 控制系統(tǒng)架構(gòu)介紹

多軸隨機(jī)振動(dòng)控制系統(tǒng)設(shè)計(jì)采用面向?qū)ο蠹肮δ苣K分層管理的設(shè)計(jì)思想，使系統(tǒng)具有易用性、通用性、可維護(hù)性、可擴(kuò)充性、可移植性等特點(diǎn)。整個(gè)系統(tǒng)遵循軟件和硬件相對(duì)獨(dú)立的設(shè)計(jì)原則，以確保通用性及可擴(kuò)展性。系統(tǒng)的架構(gòu)設(shè)計(jì)主要分成6 個(gè)層次，如圖6所示。

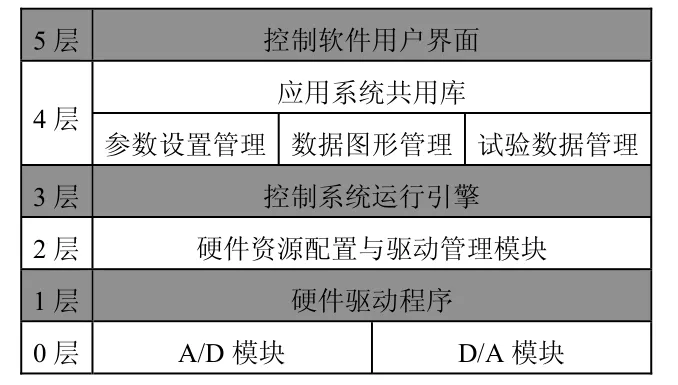
圖6 多軸隨機(jī)振動(dòng)控制系統(tǒng)層次架構(gòu) Fig.6 The framework of the multi-axis random vibration controller

2.3 試驗(yàn)參考條件

試驗(yàn)條件見(jiàn)表1。

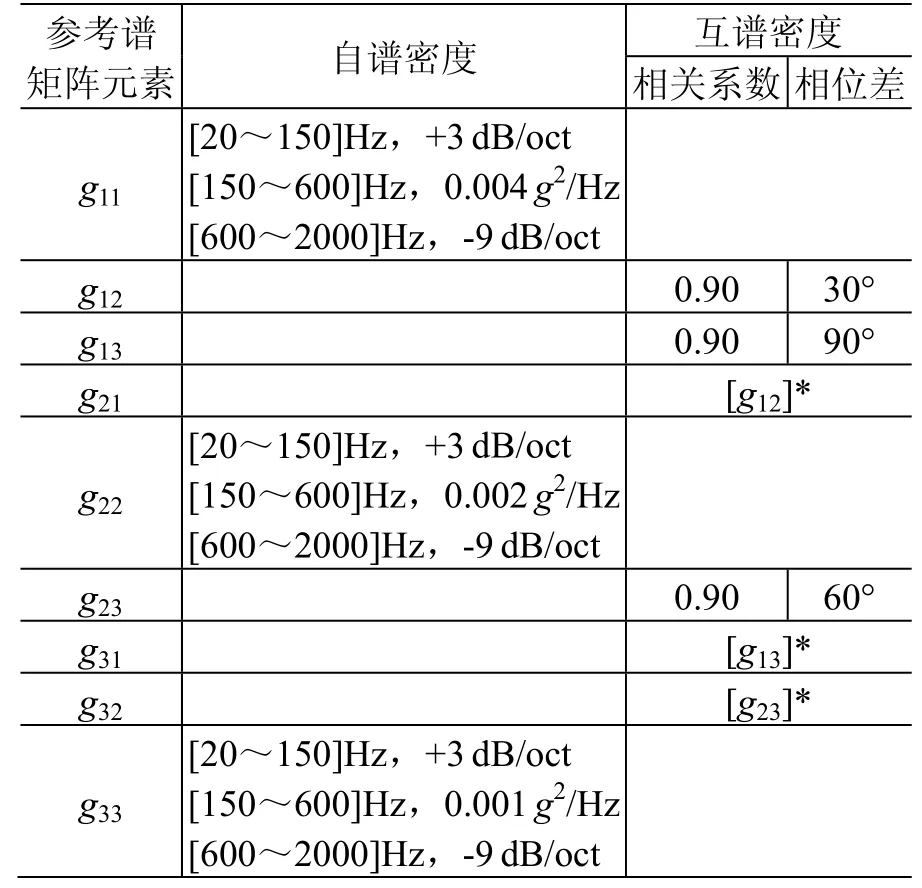
表1 三軸振動(dòng)試驗(yàn)參考條件 Table1 The reference conditions for the tri-axial vibration test

2.4 試驗(yàn)結(jié)果及分析

驗(yàn)證試驗(yàn)的3 個(gè)控制點(diǎn)布置在工作臺(tái)面上各軸向的最遠(yuǎn)端，且與各軸向保持一致（如圖5所示）。為驗(yàn)證控制算法的可行性，按表1中的試驗(yàn)條件進(jìn)行了一組三向隨機(jī)振動(dòng)試驗(yàn)。圖7為三軸向x,y,z自功率譜密度控制曲線。圖8～圖10分別給出了xy,yz和xz之間的相關(guān)系數(shù)和相位差控制曲線。

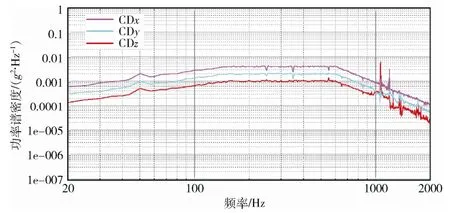
圖7 三軸向x,y,z 自功率譜密度控制曲線 Fig.7 The control curve of auto-power spectral density in x,y,z directions

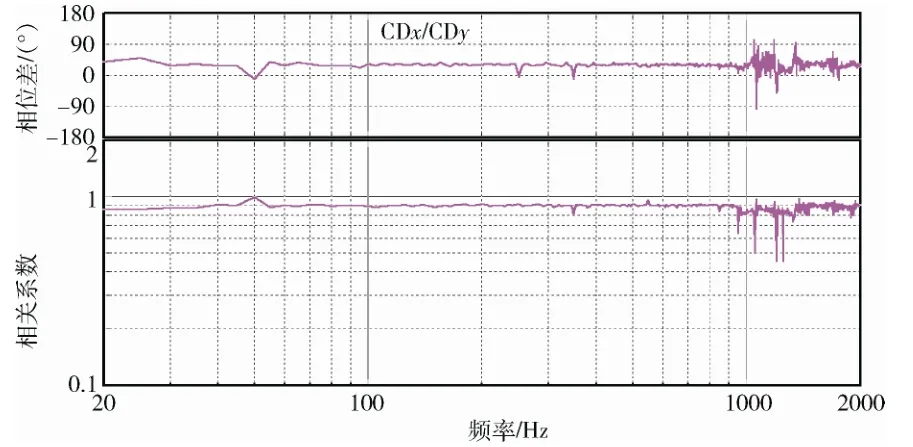
圖8 x,y 兩軸相關(guān)系數(shù)及相位差控制曲線 Fig.8 The control curve of correlation coefficient and phase difference between axes x and y

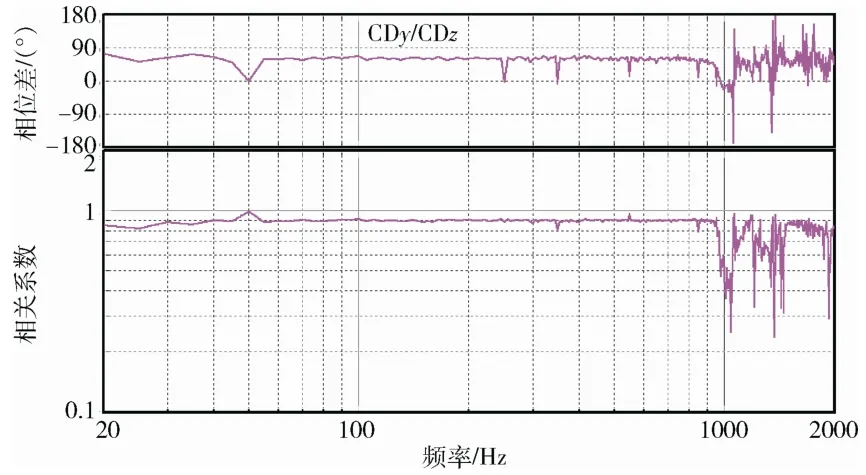
圖9 y,z 兩軸相關(guān)系數(shù)及相位差控制曲線 Fig.9 The control curve of correlation coefficient and phase difference between axes y and z

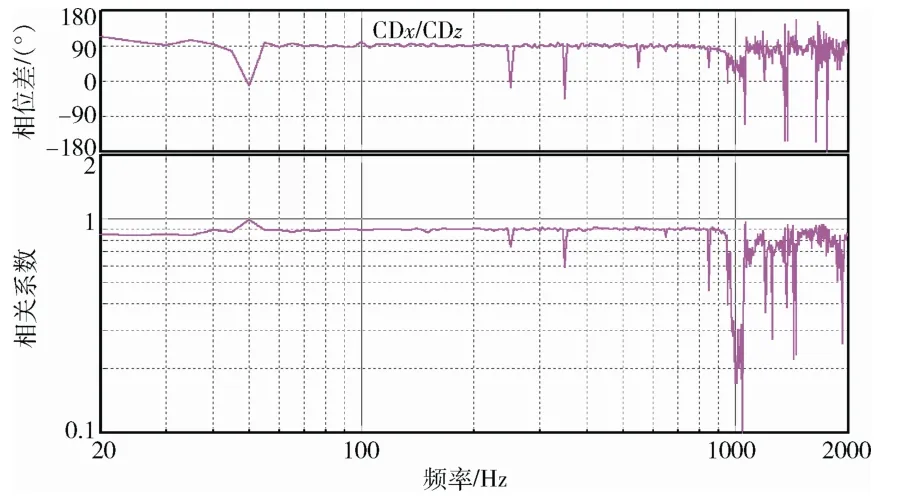
圖10 x,z 兩軸相關(guān)系數(shù)及相位差控制曲線 Fig.10 The control curve of correlation coefficient and phase difference between axes x and z

在多軸隨機(jī)振動(dòng)試驗(yàn)中，參考譜矩陣中互譜元素設(shè)置必須考慮軸與軸之間的物理可實(shí)現(xiàn)性問(wèn)題[11]。此次試驗(yàn)，x軸與y軸之間相位差為30°，y軸與z軸之間為60°，則x軸與z軸之間必須設(shè)置為90°。同時(shí)三軸之間的相關(guān)系數(shù)均設(shè)置為0.9。

研發(fā)的多軸隨機(jī)振動(dòng)控制系統(tǒng)的動(dòng)態(tài)范圍優(yōu)于80 dB。本次驗(yàn)證試驗(yàn)的頻率范圍為20～2000 Hz，譜線數(shù)為400，頻率分辨率5 Hz，統(tǒng)計(jì)自由度為120，當(dāng)試驗(yàn)條件到達(dá)0 dB 后，3 個(gè)控制點(diǎn)的自譜密度進(jìn)入容差范圍且保持基本穩(wěn)定所需的時(shí)間約為1.0 s。多軸振動(dòng)試驗(yàn)的容差控制準(zhǔn)則基于中國(guó)航天科技集團(tuán)標(biāo)準(zhǔn)Q/QJA108—2013《多維振動(dòng)試驗(yàn)方法》中8.2.2 節(jié)的容差要求[12]。從此次試驗(yàn)自譜控制曲線可以看出，控制結(jié)果除在50 Hz 和高頻若干頻點(diǎn)略有超差外，在其他試驗(yàn)頻率范圍內(nèi)的控制精度滿足不超過(guò)±3 dB 要求，且超過(guò)允差的累積帶寬小于整個(gè)試驗(yàn)頻率范圍的5%。50 Hz 頻率處超差是由三軸試驗(yàn)系統(tǒng)的50 Hz 工頻干擾引起的，可通過(guò)在功放前端引入隔離器的方法進(jìn)行屏蔽解決；而1000 Hz以上高頻若干頻率點(diǎn)超差是由于球頭和工作臺(tái)面之間耦合特性產(chǎn)生的，試驗(yàn)前可通過(guò)調(diào)整球頭相對(duì)工作臺(tái)面的位置來(lái)縮小控制超差的頻帶，而完全解 決超差問(wèn)題有一定的難度。

由于多軸振動(dòng)試驗(yàn)的復(fù)雜性，Q/QJA108—2013 標(biāo)準(zhǔn)中對(duì)控制點(diǎn)之間的相干系數(shù)和相位沒(méi)做規(guī)定。從此次試驗(yàn)控制點(diǎn)之間的相干系數(shù)和相位差控制曲線可以看出，在50 Hz 諧波頻率處和高頻處略有偏離參考條件外，在其他頻帶內(nèi)控制效果較好，其控制精度與美國(guó)SD 公司的多軸控制系統(tǒng)的控制精度基本相當(dāng)。總體而言，三軸隨機(jī)控制效果比較理想，多軸隨機(jī)控制算法的可行性得到了驗(yàn)證。研發(fā)的多軸隨機(jī)控制系統(tǒng)配合三軸振動(dòng)臺(tái)具備為航天器小型單機(jī)產(chǎn)品開(kāi)展多軸隨機(jī)振動(dòng)試驗(yàn)的能力。

3 結(jié)束語(yǔ)

本文介紹了多軸隨機(jī)振動(dòng)試驗(yàn)控制的基本理論，并應(yīng)用該理論研發(fā)了一套多軸隨機(jī)振動(dòng)試驗(yàn)控制系統(tǒng)。利用該系統(tǒng)在三軸振動(dòng)臺(tái)上進(jìn)行了一組多軸隨機(jī)振動(dòng)驗(yàn)證試驗(yàn)，結(jié)果表明本控制算法是可行的，控制效果較好。

研發(fā)的多軸隨機(jī)控制系統(tǒng)只能控制三軸三自由度振動(dòng)臺(tái)，而在控制三軸六自由度方面，還需引入輸入輸出坐標(biāo)轉(zhuǎn)換矩陣，將傳感器的線性運(yùn)動(dòng)轉(zhuǎn)換為平動(dòng)和轉(zhuǎn)動(dòng)等自由度后再進(jìn)行控制，因此該多軸隨機(jī)控制系統(tǒng)的控制功能還有待進(jìn)一步完善。隨著多軸控制技術(shù)的不斷發(fā)展，它將在今后力學(xué)環(huán)境試驗(yàn)領(lǐng)域發(fā)揮越來(lái)越廣泛的作用。

（References）

[1] 樊世超,馮咬齊.多維動(dòng)力學(xué)環(huán)境模擬試驗(yàn)技術(shù)研究[J].航天器環(huán)境工程,2006,23(1): 23-28 Fan Shichao,Feng Yaoqi.Study on multi-DOF dynamic environment simulation technology[J].Spacecraft Environment Engineering,2006,23(1): 23-28

[2] Himelblau H,Hine M J.Effects of triaxial and uniaxial random excitation on the vibration response and fatigue damage of typical spacecraft hardware[C]∥Proceedings of the 66thShock and Vibration Symposium,SAVIAC.California,1995: 15-32

[3] Keller T,Underwood M A.An application of MIMO techniques to satellite testing[C]∥Proceedings: Institute of Environmental Sciences and Technology,2001: 327-339

[4] MIL-STD-810G Department of defense test method standard: Environmental engineering considerations and laboratory test: method 527,multi-exciter tests[S],2008- 10-31

[5] 祝濟(jì)之,楊志鵬.多維隨機(jī)振動(dòng)試驗(yàn)中的互譜控制技術(shù)[J].航天器環(huán)境工程,2010,27(5): 621-624 Zhu Jizhi,Yang Zhipeng.Cross-spectral control technique in multi-dimensional random vibration test[J].Spacecraft Environment Engineering,2010,27(5): 621-624

[6] Smallwood D O.Random vibration testing of a single test item with a multiple input control system[C]// Proceedings of Institute of Environmental Sciences.Dallas,USA,1982: 42-49

[7] Smallwood D O.Multiple shaker random control with cross coupling[C]//Proceedings of the IES,1978: 341-347

[8] Smallwood D O.Minimum drive requirements for a multiple input multiple output linear system[C]∥Proceedings: Institute of Environmental Sciences and Technology,1986: 295-301

[9] Peeters B,Debille J.MIMO random vibration qualification testing: algorithm and practical experiments[C]//Proceedings of ESTECH 2002.Anaheim,CA,2002: 1-12

[10] Underwood M A.Multi-exciter testing applications: theory and practice[C] ∥Proceedings: Institute of Environmental Sciences and Technology.Anaheim,CA,2002: 1-10

[11] Underwood M A,Keller T.Understanding and using the spectral density matrix[C]∥Proceedings of the 76thShock ＆Vibration Symposium.Destin,FL,2005: 1-16

[12] Q/QJA108—2013 多維振動(dòng)試驗(yàn)方法[S].中國(guó)航天科技集團(tuán)公司,2013