多思善想 以少勝多

摘要:高考是注重能力的考試,特別是學生運用數學知識和方法分析問題和解決問題的能力更是考查的重點。為了提高能力,解題之后要思改進與優化,思數形找妙法,思引申與推廣,從“題海”中解脫出來,以少勝多。
關鍵詞:提高能力;多思善想;以少勝多
中圖分類號:G632.0 ? ? 文獻標志碼:A ? ? 文章編號:1674-9324(2015)44-0180-02
近幾年的素質教育中,強調較多的是如何提高學生分析問題、解決問題的能力。要做到這一點,必須在平時的學習過程中一點一滴地積累和培養。有很多學生感到疑惑:“做了許多數學練習,解題能力為何沒有明顯提高?”究其原因,往往在于解題之后滿足于題已解出而淺嘗輒止。然而,“正確”≠“完美”,為了達到完美,為了提高能力,解題之后還應多思善想。怎樣才算多思善想呢?請看如下“三思”。
一、思改進與優化
解題開始時,重在找到已知與未知的聯系,能達到目的走點彎路也無所謂,但是,解出之后,就應回頭查看,論證中有無多余的枝節可刪去?復雜運算能否簡化?哪些量在變,哪些量不變?換一個角度去考慮,有無更簡單的解法?這樣去深究,解題的關鍵才能得以突出,因而也會給我們留下深刻的印象,并在今后由此及彼的加以靈活運用。
例1:已知f(x+1)=x ?+x+1,那么f(x-1)的最小值是
。
分析:按常規解法,應由f(x+1)→f(x)→f(x-1),求出f(x-1)的解析式后再求其最小值。仔細觀察可發現所求最小值與f(x+1)的最小值相同,均為 ?,為什么呢?深究根底,發現f(x-1)的圖像可由f(x+1)的圖像向右平移兩個單位得到,他們當然有相同的最小值,因此,只需求出f(x+1)的最小值即可。
f(x+1)=(x+ ?) ?+ ?≥
例2:(2013年理)設等差數列{a ?}的前n項和為s ?,s ?=-2,s ?=0,s ?=3,則m= ? ?。
A. 3 ? B. 4 ? C. 5 ? D. 6
分析:設數列{a ?}的首項為a ?,公差為d,則
(m-1)a ?+ ?d=-2ma ?+ ?d=0(m+1)a ?+ ?d=3,解出m=5
仔細觀察可發現s ?-s ?=a ?,s ?-s ?=a ?,所以
d=a ?-a ?=1,再由a ?+m=3ma ?+ ?d=0,解出m=5
二、思數形找妙法
數形結合是很重要的一種數學思想,也是培養發展學生思維的有效途徑。大多數代數問題都有幾何背景,若拘于常規,會有很大的運算量,甚至思維受阻,若結合圖形及其特征常能快速求解。
例3:(2013課標全國卷Ⅱ)若存在正數x使2 ?(x-a)<1成立,則a的取值范圍是 ? ?。
A.(-∞,+∞) ? ? B.(-2,+∞)
C.(0,+∞) ? ? ?D.(-1,+∞)
分析:求解此類問題僅從“數”上觀察較難入手,但如果把數量關系轉化為圖形語言,借助函數圖像的生動性和直觀性闡明數量之間的關系,即可快速判斷參數的取值范圍。
解析:不等式2 ?(x-a)<1可變形為x-a<( ?)
在同一平面直角坐標系內做出直線y=x-a與y=( ?) ?的圖像,如圖。
由題意可知,在(0,+∞)上,直線y=x-a有一部分在曲線y=( ?) ?的下方。觀察可知,有-a<1,所以a>1,故選D。
例4:(2014江蘇高考)已知f(x)是定義R在 ? ? 上且周期為3的函數,當x∈[0,3)時,f(x)=|x ?-2x+ ?|,若函數y=f(x)-a在區間[-3,4]上有10個零點(互不相同),則實數a的取值范圍是 ? ?。
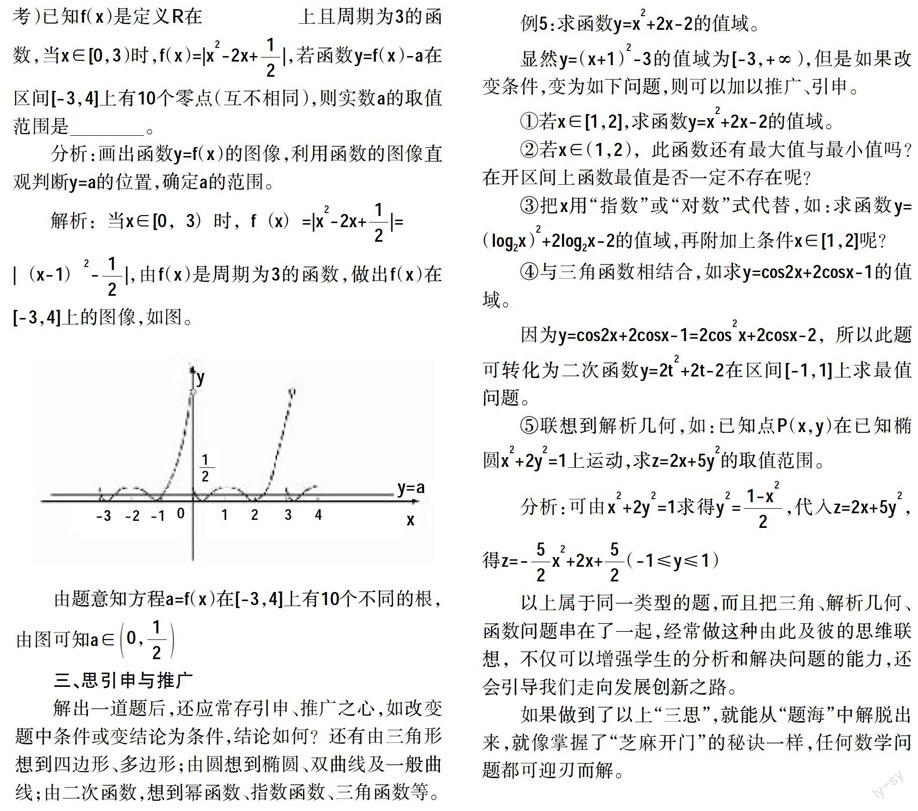
分析:畫出函數y=f(x)的圖像,利用函數的圖像直觀判斷y=a的位置,確定a的范圍。
解析:當x∈[0,3)時,f(x)=|x ?-2x+ ?|=
|(x-1) ?- ?|,由f(x)是周期為3的函數,做出f(x)在[-3,4]上的圖像,如圖。
由題意知方程a=f(x)在[-3,4]上有10個不同的根,由圖可知a∈0,
三、思引申與推廣
解出一道題后,還應常存引申、推廣之心,如改變題中條件或變結論為條件,結論如何?還有由三角形想到四邊形、多邊形;由圓想到橢圓、雙曲線及一般曲線;由二次函數,想到冪函數、指數函數、三角函數等。
例5:求函數y=x ?+2x-2的值域。
顯然y=(x+1) ?-3的值域為[-3,+∞),但是如果改變條件,變為如下問題,則可以加以推廣、引申。
①若x∈[1,2],求函數y=x ?+2x-2的值域。
②若x∈(1,2),此函數還有最大值與最小值嗎?在開區間上函數最值是否一定不存在呢?
③把x用“指數”或“對數”式代替,如:求函數y=(log ? ?x) ?+2log ?x-2的值域,再附加上條件x∈[1,2]呢?
④與三角函數相結合,如求y=cos2x+2cosx-1的值域。
因為y=cos2x+2cosx-1=2cos ?x+2cosx-2,所以此題可轉化為二次函數y=2t ?+2t-2在區間[-1,1]上求最值問題。
⑤聯想到解析幾何,如:已知點P(x,y)在已知橢圓x ?+2y ?=1上運動,求z=2x+5y ?的取值范圍。
分析:可由x ?+2y ?=1求得y ?= ?,代入z=2x+5y ?,得z=- ?x ?+2x+ ?(-1≤y≤1)
以上屬于同一類型的題,而且把三角、解析幾何、函數問題串在了一起,經常做這種由此及彼的思維聯想,不僅可以增強學生的分析和解決問題的能力,還會引導我們走向發展創新之路。
如果做到了以上“三思”,就能從“題海”中解脫出來,就像掌握了“芝麻開門”的秘訣一樣,任何數學問題都可迎刃而解。

