基于擴張狀態觀測器的導彈滑模制導律

張堯，郭杰，唐勝景，馬悅悅，商巍

(北京理工大學 宇航學院，飛行器動力學與控制教育部重點實驗室，北京100081)

制導律設計是導彈實現精確控制和對目標實現準確打擊的基礎.因此，要實現更高精度的制導律設計，就需要在原有的制導模型基礎上采用更為先進的控制算法進行制導律設計.

隨著控制思想的進步，相關研究提出了諸如最優制導律、滑模變結構制導律、改進比例導引等.Zhang等［1］基于線性二次調節理論，以脫靶量和攻擊落角為約束，設計了空地導彈的三維最優制導律;Hexner等［2］在導彈機動加速度物理約束條件下，基于隨機優化控制思想建立零化脫靶量的條件可能密度函數，提出了一種全新的最優制導律，但當導彈加速度物理約束足夠大時，該方法退化為傳統的最優制導律;張友安等［3］考慮到落角約束，應用Schwarz不等式得到了任意加權最優制導律的一般表達式，但導彈的落角和加速度指令受初始條件影響較大;而Zhang等［4］基于非線性積分滑模控制設計了一種變結構制導律，同時采用非線性擾動觀測器對制導律目標機動加速度進行觀測和控制量補償，降低了控制量的高頻振蕩，實現了視線角速率在有限時間內收斂于零;朱凱等［5］基于滑模干擾觀測器和比例導引律設計了一種多約束條件下的魯棒末制導方法，該制導方法不需要測距信息和對剩余飛行時間的估算，但在制導指令生成過程中需要對導引系數不斷進行自適應迭代運算，從而加大了指令計算時間和系統的復雜性;馬克茂等［6］和竇榮斌等［7］均是采用滑模控制思想設計了變結構制導律，但設計過程中將系統中的不確定項視為未知有界的，使得所需控制量變大并且容易產生高頻振蕩現象;熊俊輝等［8］針對迎擊攔截高速目標的問題，應用模糊變系數策略設計了一種全新的變結構制導律，降低了制導初期的需用過載.此外，Moosapour等［9］通過考慮自動駕駛儀動態特性，基于魯棒設計思想提出了一種改進比例導引設計方法;王嘉鑫等［10］通過引入參考目標設計了一種新型的比例導引律，但該方法只適用于目標機動性較小的情況.

上述新型制導律雖然具備很強的優越性，但其設計增加了系統自身的復雜度，同時對于導彈運動過程中的未知量(如目標機動加速度)無法進行實時的準確測量，工程應用不強.在滑模變結構制導律設計中通過狀態觀測器對目標機動加速度進行估計，但實際系統中由于系統自身和外界的不確定性，導致設計前假設的目標機動加速度上限無法準確獲得，獨立于模型的設計能力差，人為假設的上限值會使所需的控制量變大并且可能出現高頻顫振現象，打破原有的系統物理條件約束.

針對上述不足，本文以導彈攔截機動目標為背景，采用的擴張狀態觀測器(ESO，Extended State Observer)在獨立于被控對象數學模型的基礎上，通過將目標機動加速度擴張成一個新的狀態而對這一新的狀態量進行實時的估計和動態補償;同時，基于滑模變結構理論提出了一種新型滑模制導律，從而實現對機動目標的精確打擊.

1 導彈運動模型

1.1 模型描述

為了方便研究，考慮縱向平面內的攔截彈制導律設計問題.彈目相對運動如圖1所示.圖中，M和T分別表示導彈和目標的質心位置.

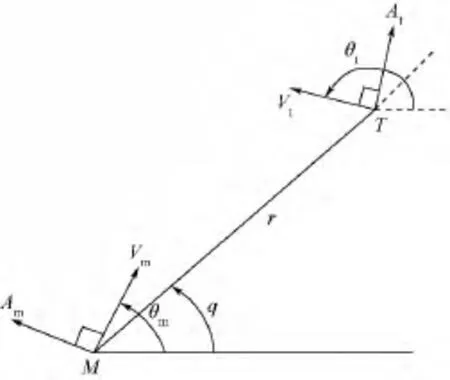
圖1 彈目相對運動Fig.1 Missile-to-target relative motion

由彈目相對運動方程可知:

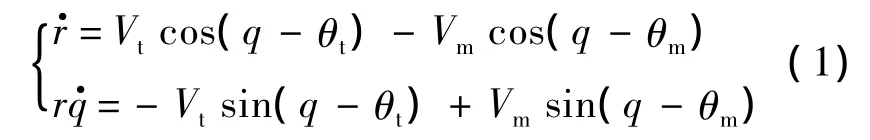
式中，r為彈目相對距離;q為彈目視線角;Vt和Vm分別表示目標速度和導彈速度.為簡化數學模型，假設目標和導彈的速度大小對時間的導數=0和=0.此外，令目標和導彈的法向加速度分別為At=Vt，Am=Vm，其中θt和θm分別為目標和導彈的航跡傾角，和分別為目標和導彈的航跡傾角對時間的導數.

因此，式(1)兩邊對時間t求導，可得

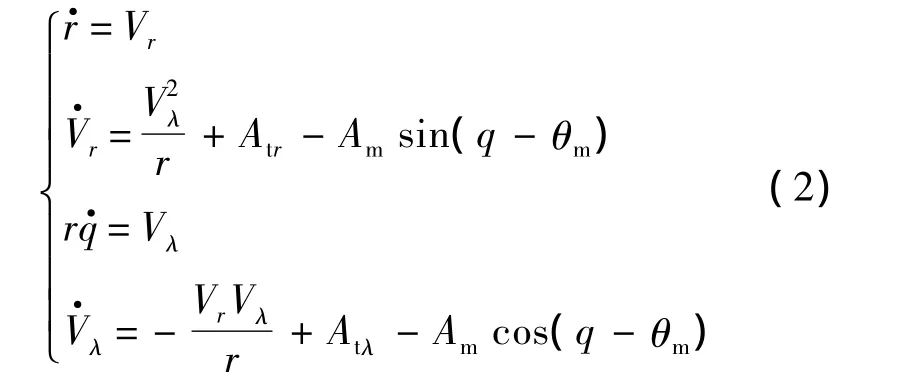
假設1 系統(2)中各個狀態變量r，q，Vr，Vλ和 θm均可直接得到［11］.

假設2 在導彈對目標實施攔截打擊過程中，目標法向加速度At是未知有界的，則Atr和Atλ滿足如下關系［11］:

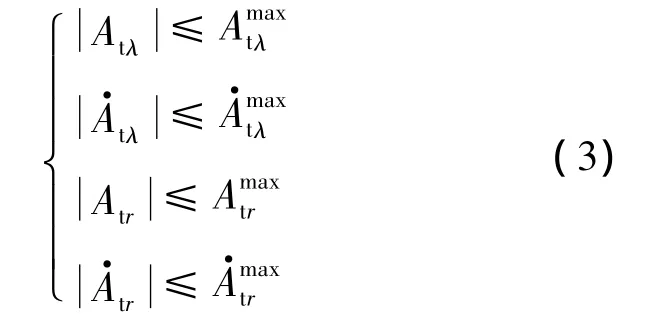
1.2 攔截策略

式中c0為設計參數且c0＞0.令，則要實現攔截策略(4)需設計一個在有限時間內可令e趨于零的反饋控制器.該攔截制導策略的有效性證明詳見文獻［11］.

2 基于ESO的導彈滑模制導律設計

為了使導彈實現1.2節所述攔截策略，本文采用滑模控制理論來對導彈制導律進行設計.對于系統(2)，選取滑模面為

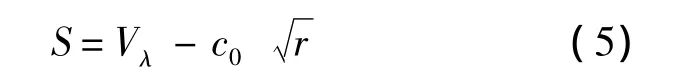
根據滑模運動的可達性條件，令S對時間t求導，采用如下趨近律:

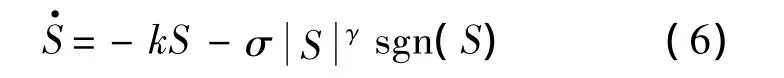
式中，趨近律設計參數 k＞0，σ ＞0，0＜γ ＜1.該趨近律能夠保證閉環系統(2)的狀態軌跡以有限時間收斂于滑模面S的鄰域內.

取閉環系統(2)的控制量u=Am，式(5)對時間求導，并聯立式(2)和式(6)，則

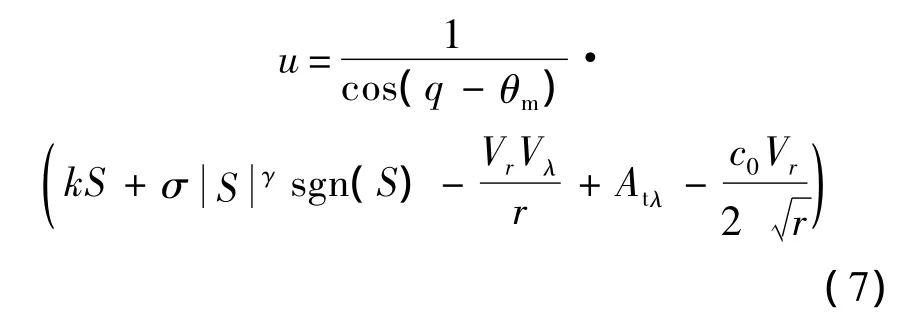
在實際工程應用中，系統無法快速準確獲得Atλ的大小.故本文采用ESO對閉環系統(2)中的未知項Atλ進行實時的觀測和動態補償.

將系統(2)中的未知項擴張為一個新的狀態，構成如下所示的系統:

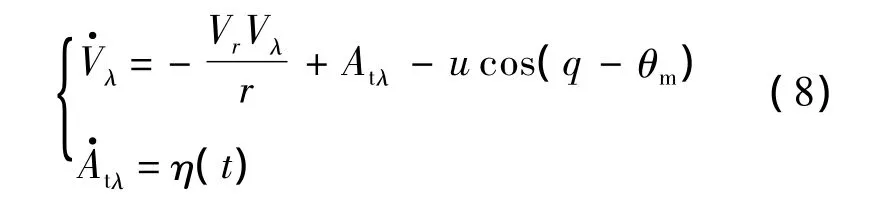
式中，函數η(t)為目標加速度分量Atλ的導數，則對系統(8)設計二階擴張狀態觀測器，其數學模型為

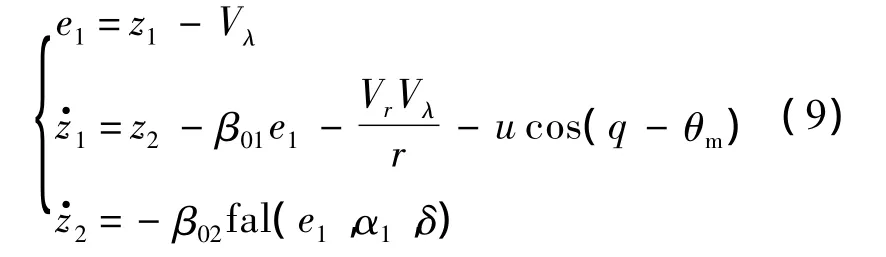
式中，e1為ESO對系統狀態量的觀測誤差;z1和z2為ESO對系統(8)的狀態觀測值;β01和 β02為ESO的觀測增益;函數fal(·)的表達式如下所示:

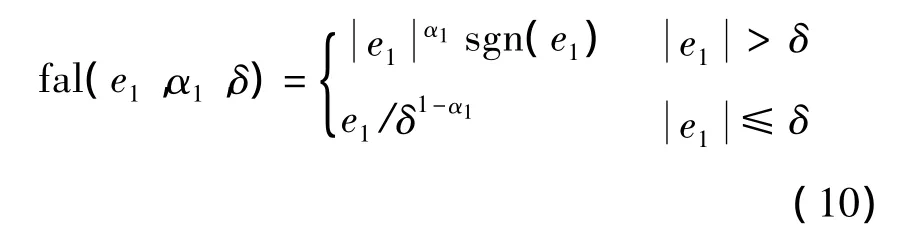
其中α1和δ為ESO的設計參數.通過選擇合適的β01和β02可以使得ESO能夠很好地對狀態Vλ和被擴張狀態Atλ進行觀測和動態補償［13］.

因此，聯立式(7)和式(9)可得基于ESO的導彈滑模制導律(ESMG)的控制量為

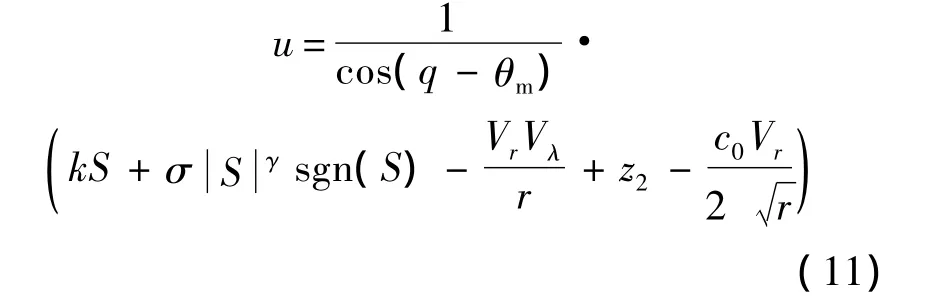
同時，本文在制導律仿真過程中考慮自動駕駛儀的動態特性，將自動駕駛儀視為二階振蕩環節，則通過自動駕駛儀輸入給彈體環節的控制指令Amc滿足下式:

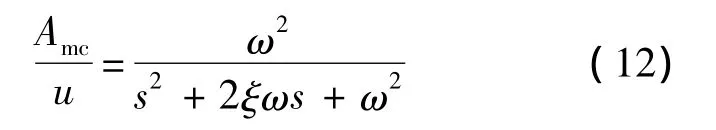
針對本文所設計的滑模制導律，存在合適的β01，β02，α1和 δ，使得觀測值 z1和 z2分別收斂于Vλ和Atλ的鄰域內，通過采用控制律(11)，使閉環系統(2)中各個狀態的運動軌跡以有限時間收斂于滑模面S=0附近.

3 穩定性證明

為了便于系統的穩定性分析，首先給出如下引理.

引理1［14］假設V(x)是定義域為U?Rn且一階連續可導的正定函數，V·(x)+λVα(x)是定義域為U?Rn的半負定函數，其中α∈(0，1)，λ∈R+.則存在定義域U0?Rn，使得定義在U0?Rn上的任意V(x)均能以有限時間收斂至零.同時，若Treach為V(x)收斂至零的時間，則

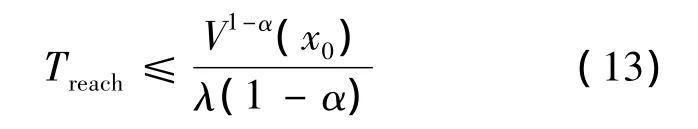
式中V(x0)為V(x)的初值.

文獻［15］給出了ESO的穩定性證明.此處將不再論述.當 β02取值足夠大、β01取值足夠小，則ESO的觀測誤差趨于零，也就是說ESO的觀測量z1和z2分別以有限時間收斂于Vλ和Atλ的鄰域內.

大量數值仿真實驗表明，非線性函數fal中的參數選擇 α1=1/2n－1，δ=h，其中 n 為擴張狀態觀測器的階數，h為積分步長.當α1和δ確定時，根據系統的時間尺度概念，參數β0i(i=1，2)基本與積分步長有關，由工程經驗可知:β01≈1/h，β02≈h2/3［15］.

針對系統(8)構造如下的Lyapunov函數:

對式(14)按時間t求導可得

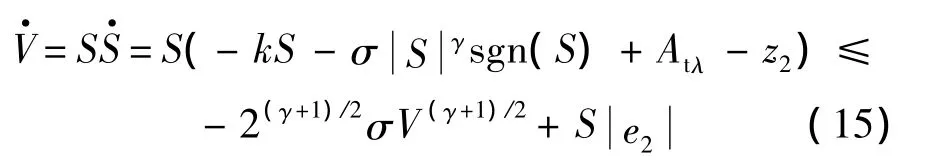
假設存在一個權數0＜ε≤1，使得不等式(15)可以寫成

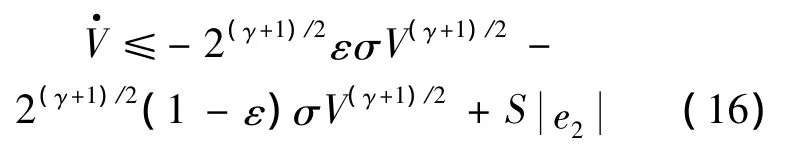
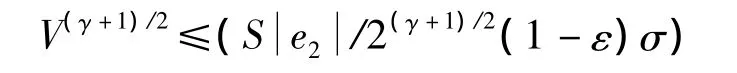
系統收斂性得證，且S滿足:

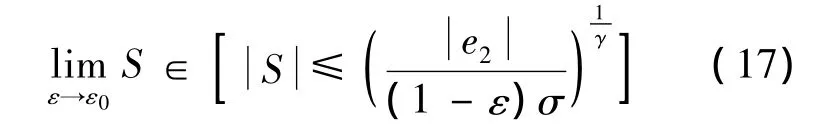
式中0＜ε0＜1.同時，函數 V收斂至零的時間Treach滿足下式:

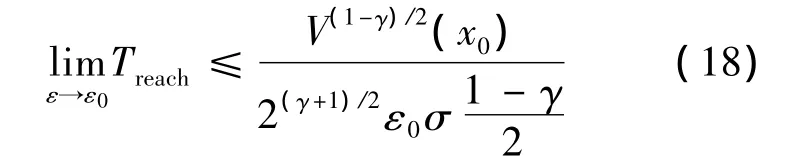
因此，當ESO穩定時，通過調節控制律中k和σ的值可使閉環系統的軌跡收斂于滑模面S=0的鄰域內.

當ESO能夠準確估計系統中的不確定項時，參數k和σ越大，閉環系統中各個狀態量以有限時間的收斂性越好，系統所取的滑模面S越能趨近于零;然而，在實際問題中，過大的k和σ會使得控制量過大而超過導彈系統自身物理條件的限制，因此在系統參數整定時需要權衡考慮設計方法和實際物理條件對參數的影響.

4 仿真結果分析

選取導彈的初始位置為 xm(0)=0 m，ym(0)=0 m，目標的初始位置為xt(0)=20 km，yt(0)=20 km;c0=0.1;導彈導引頭對視線角速率測量需經過時間常數為30 ms的一階慣性環節;導彈的最大機動過載為20;導彈在攔截過程中速度滿足下述關系:

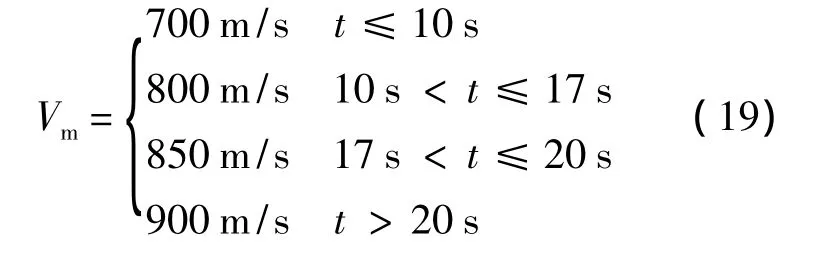
此外，導彈自動駕駛儀的二階動態特性相關參數為 ω =10，ξ=0.7.

在所設計的ESMG中，開關函數sgn(·)的滯后性會使控制量Am在實際仿真過程中產生高頻抖振現象，進而影響了系統本身的穩定性，使導彈命中精度降低.在制導律設計時，為削弱控制量的抖振現象，采用連續函數sat(·)代替式(11)中的開關函數.

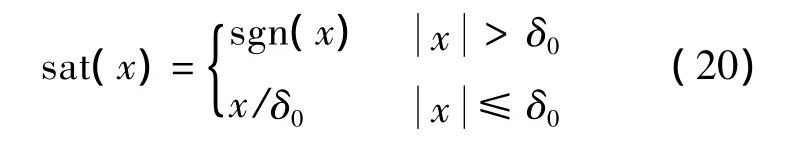
式中 δ0為消顫因子，δ0=0.01.

為驗證所設計制導律的優越性，與基于有限時間收斂理論設計的導引律(FTCG)［12］進行對比，其數學模型為

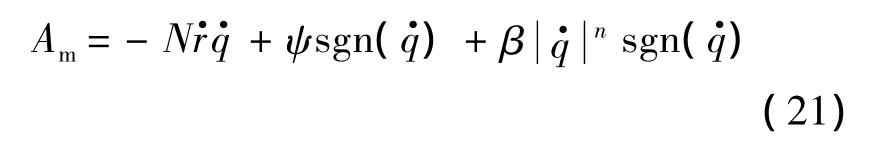
式中，N＞2;β＞0;0＜n≤1;ψ為目標機動加速度的上界，ψ =100.

針對上述制導律設計方法，對下面算例中的3種情況進行對比仿真.仿真中，ESMG的模型參數統一取為:γ =0.5，k=1.25，σ =1.2，β01=50，β02=100，α1=0.2，δ=0.15.

算例1 目標作法向加速度為At=10g sin t(單位:m/s2)的高速機動.

1)迎擊攔截速度為480 m/s的目標.

針對這種情況，取導彈的初始航跡角分別為θ =90°，45°，0°，FTCG 中 N=3.3，β =10，n=0.5，導彈與目標的運動曲線如圖2(a)所示.不同初始航跡角下，ESMG得到的脫靶量分別為 0.16，0.96，0.82 m，而 FTCG 得到的脫靶量分別為0.53，1.38，1.48 m.

2)尾追攔截速度為480 m/s的目標.

針對這種情況，取導彈的初始航跡角分別為θ =90°，45°，0°，FTCG 中 N=10，β =10，n=0.5，導彈與目標的運動曲線如圖2(b)所示.不同初始航跡角下，ESMG得到的脫靶量分別為 0.70，0.16，0.03 m，而 FTCG 得到的脫靶量分別為8.02，5.31，4.06 m.

3)前向攔截速度為1100 m/s的目標.

針對這種情況，取導彈的初始航跡角分別為θ =90°，45°，0°，FTCG 中 N=10，β =10，n=0.5，導彈與目標的運動曲線如圖2(c)所示.不同初始航跡角下，ESMG得到的脫靶量分別為1.26，1.31 m，而 FTCG 得到的脫靶量分別為10.05，11.37 m.

算例2 為進一步驗證ESMG在目標的法向加速度非周期變化時的有效性，考慮Case 1中的3種攔截方式對非周期高速機動目標進行攔截.目標法向加速度如圖3所示.

1)迎擊攔截速度為480 m/s的目標.

取導彈的初始航跡角與制導律中相關參數同算例1，導彈與目標的運動曲線如圖4(a)所示.不同初始航跡角下，ESMG得到的脫靶量分別為0.47，0.76，0.68 m，而 FTCG 得到的脫靶量分別為 8.16，8.15，8.17 m.

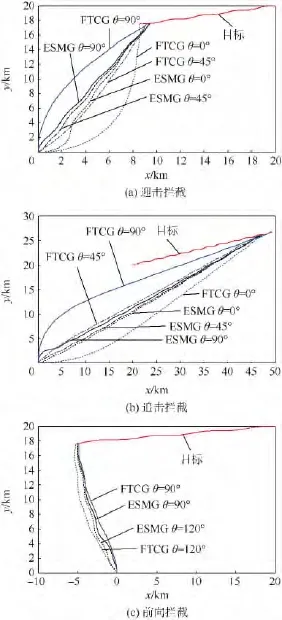
圖2 算例1中彈目相對運動曲線Fig.2 Curves of relative motion between missile and target in Case 1

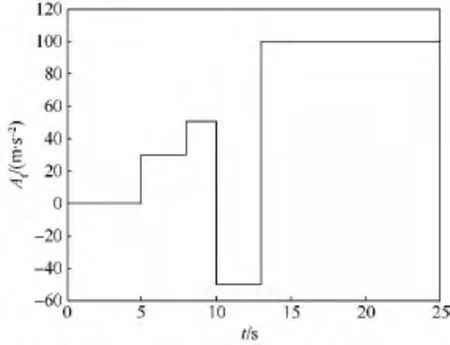
圖3 目標法向加速度Fig.3 Normal acceleration of target

2)尾追攔截速度為480 m/s的目標.

取導彈的初始航跡角與制導律中相關參數同算例1，導彈與目標的運動曲線如圖4(b)所示.不同初始航跡角下，ESMG得到的脫靶量分別為1.47，1.14，1.49 m，而 FTCG 得到的脫靶量分別為 14.23，14.31，14.17 m.

3)前向攔截速度為1100 m/s的目標.

取導彈的初始航跡角與制導律中相關參數同算例1，導彈與目標的運動曲線如圖4(c)所示.不同初始航跡角下，ESMG得到的脫靶量分別為0.41，0.52 m，而 FTCG 得到的脫靶量分別為9.72，10.17 m.

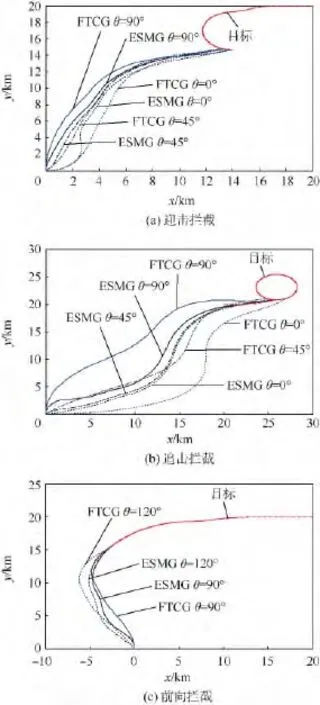
圖4 算例2中彈目相對運動曲線Fig.4 Curves of relative motion between missile and target in Case 2

由上述對比仿真結果可以看出，ESMG使導彈在攔截時間和脫靶量方面均要小于FTCG.同時，針對不同的初始航跡角和攔截方法，ESMG表現出在導彈運動方面更強的魯棒性，導彈運動軌跡和脫靶量受攔截初始條件的不同影響更小.ESMG可以使導彈在不同攔截策略下以更大的精度對高速機動目標實施攔截打擊.

由于篇幅所限，圖5僅給出了初始航跡角θ=90°時導彈以上述3種攔截方式攔截目標的法向過載變化曲線，雖然在導彈運動初期ESMG對導彈的需用過載要求比較大，但在導彈真正實施對機動目標的攔截打擊末制導段時，ESMG所需的最大過載小于FTCG.因此，ESMG降低了導彈攔截末段的需用過載，提高了導彈武器的可靠性，在導彈可用過載一定的情況下，能夠使導彈有效地攻擊機動性更高的目標.

圖6給出了初始航跡角為θ=90°時導彈迎擊攔截機動目標時導彈控制輸入量變化曲線，由于仿真中考慮自動駕駛儀的二階動態特性，控制量Am的真實響應具有一定的振蕩和時滯特性，間接驗證了所設計制導律的實用性.

如圖7所示，采用所設計的狀態反饋控制律能夠保證滑模面在有限時間內趨近于零，從而實現對導彈所設計的攔截策略(2).

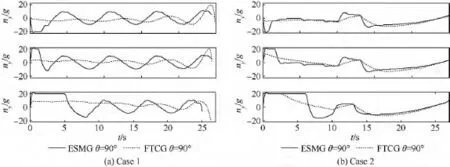
圖5 不同攔截方式(θ=90°)下導彈法向過載變化曲線Fig.5 Curves of missile normal overload in different intercepting ways(θ=90°)

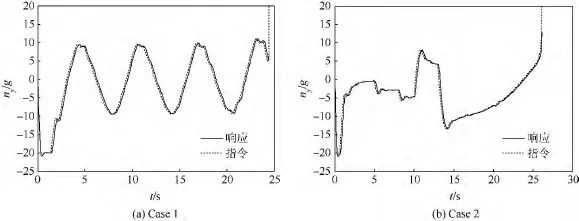
圖6 控制輸入量變化曲線Fig.6 Variation curves of control input

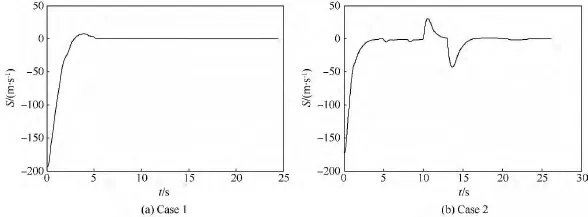
圖7 滑模面變化曲線Fig.7 Variation curves of sliding mode surface

圖8為ESO對未知目標加速度的觀測曲線.通過ESO對目標加速度的實時觀測和補償，實現了降低導彈攔截末端需用過載的目的.

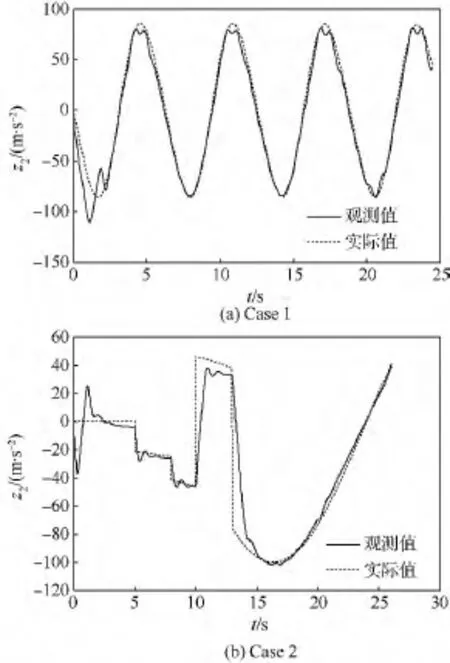
圖8 ESO對未知項加速度的觀測曲線Fig.8 Curves of estimated value of ESO to acceleration of unknown term

5 結論

本文在傳統變結構制導律的基礎上提出了一種新的滑模制導律，經仿真驗證表明:

1)本文所設計制導律中的擴張狀態觀測器能夠實時地對目標機動加速度進行跟蹤觀測和反饋補償，達到了減小導彈打擊過程中需用過載的目的.

2)針對導彈采用不同的攔截策略打擊各種快速高機動目標的問題，本文所設計的制導律能夠保證導彈以更短的時間、更小的末端需用過載實現對目標的精確打擊.

References)

［1］ Zhang Q Z，Wang Z B，Tao F.Optimal guidance law design for impact with terminal angle of attack constraint［J］.Optik，2014，125(1):243-251.

［2］ Hexner G，Shima T.Stochastic optimal control guidance law with bounded acceleration［J］.IEEE Transaction on Aerospace and Electronic Systems，2007，43(1):71-78.

［3］ 張友安，黃詰，孫陽平.帶有落角約束的一般加權最優制導律［J］.航空學報，2014，35(3):848-856.Zhang Y A，Huang J，Sun Y P.Generalized weighted optimal guidance laws with impact angle constraint［J］.Acta Aeronautica et Astronautica Sinica，2014，35(3):848-856(in Chinese).

［4］ Zhang Z X，Li S H，Luo S.Terminal guidance laws of missile based on ISMC and NDOB with impact angle constraint［J］.Aerospace Science and Technology，2013，31(1):30-41.

［5］ 朱凱，齊乃明.基于滑模干擾觀測器的垂直攻擊末制導律研究［J］.兵工學報，2011，32(12):1462-1467.Zhu K，Qi N M.Research on vertical impact terminal guidance law based on sliding mode disturbance observer［J］.Acta Armamentrii，2011，32(12):1462-1467(in Chinese).

［6］ 馬克茂，馬杰.機動目標攔截的變結構制導律設計與實現［J］.宇航學報，2010，31(6):1589-1595.Ma K M，Ma J.Design and implementation of variable structure guidance law for maneuvering target interception［J］.Journal of Astronautics，2010，31(6):1589-1595(in Chinese).

［7］ 竇榮斌，張科.基于二階滑模的再入飛行器末制導律研究［J］.宇航學報，2011，32(10):2109-2114.Dou R B，Zhang K.Research on terminal guidance law for re-entry vehicle based on second-order sliding mode control［J］.Journal of Astronautics，2011，32(10):2109-2114(in Chinese).

［8］ 熊俊輝，唐勝景，郭杰，等.基于模糊變系數策略的迎擊攔截變結構制導律設計［J］.兵工學報，2014，35(1):134-139.Xiong J H，Tang S J，Guo J，et al.Design of variable structure guidance law for head-on interception based on variable coefficient strategy［J］.Acta Armamentarii，2014，35(1):134-139(in Chinese).

［9］ Moosapour S S，Alizadeh G，Khanmohammadi S，et al.A novel robust proportional navigation guidance law design for missile considering autopilot dynamic［J］.Transactions of the Institute of Measurement and Control，2013，35(3):703-710.

［10］ 王嘉鑫，林德福，宋韜.引入參考目標的比例導引制導律研究［J］.航天控制，2013，31(6):31-35.Wang J X，Lin D F，Song T.The proportional navigation guidance law with reference object［J］.Aerospace Control，2013，31(6):31-35(in Chinese).

［11］ Shtessel Y，Shkolnikov L，Levant A.Guidance and control of missile interceptor using second-order sliding modes［J］.IEEE Transaction on Aerospaceand ElectronicSystems，2009，45(1):110-124.

［12］ Zhou D，Sun S.Guidance laws with finite time convergence［J］.Journal of Guidance，Control，and Dynamics，2009，32(6):1838-1846.

［13］ 馬悅悅，唐勝景，郭杰，等.基于自抗擾和模糊邏輯的大攻角控制系統設計［J］.系統工程與電子技術，2013，35(8):1711-1716.Ma Y Y，Tang S J，Guo J，et al.High angle of attack control system design based on ADRC and fuzzy［J］.Systems Engineering and Electronics，2013，35(8):1711-1716(in Chinese).

［14］ Bhat S P，Bernstein D S.Finite-time stability of continuous autonomous systems［J］.SIAM Journal of Control and Optimization，2000，38(8):751-766.

［15］ 韓京清.自抗擾控制技術——估計補償不確定因素的控制技術［M］.北京:國防工業出版社，2008:221-237.Han J Q.Active disturbance rejection control technique:the technique for estimating and compensating the uncertainties［M］.Beijing:National Defence Industry Press，2008:221-237.