一個類Lorenz系統的Hopf分岔分析及分岔控制

張中華，付景超，鄧冠男

（東北電力大學理學院，吉林 吉林132012）

0 引言

1963年，美國著名氣象學家E.N.Lorenz在刻畫熱對流不穩定性時發現了第一個混沌系統，即Lorenz系統［1］，其動力學方程表示為

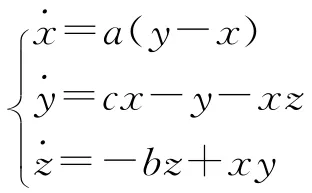
其中，x為對流強度，y為上升流和下降流的溫差，z為鉛直方向溫度分布的非線性強度。c為Rayleigh數，為系統的主要控制參數，a是Prandt數，b是外形比。當參數時，上述系統有混沌吸引子［2－3］。

自Lorenz發現第一個混沌系統之后，人們開始不斷尋找新的混沌系統，并發現了許多新的混沌系統，如Chua系統、Chen系統、Qi系統等，對這方面的研究也很多［4－7］。1994年，Sprott利用計算搜索的方法提出了19種簡單形式的三階二次混沌系統［8］，但對其中的系統進行分析的文獻不多。文獻［9］介紹了三維二次多項式自治混沌系統中不滿足Shil′nikov定理條件的一種特殊系統，即著名的Sprott C系統：并在此基礎上提出了一個新的混沌系統（稱廣義Sprott系統）：進一步研究了該系統的Hopf分岔及周期解穩定性。2008年，楊啟貴和陳關榮提出了一個新的三維混沌系統［10］文獻［11］在此基礎上構造了一個新的四維自治超混沌系統，研究了系統的基本動力學行為，并設計自適應追蹤控制器，實現對各種不同參考信號的單變量追蹤控制。文獻［12］研究了新的三維自治連續時間類Lorenz系統平衡點的存在性與穩定性，并給出了系統發生Hopf分岔和余維二退化Hopf分岔的參數條件。但上述研究主要集中在混沌的同步和控制方面，對分岔控制的研究相對較少。

本文針對文獻［12］中的模型，主要研究該模型的Hopf分岔行為及分岔控制問題。

1 新的類Lorenz系統模型

考慮模型：

其中，x，y，z為狀態變量，a，b，c為系統參數。

1.1 平衡點穩定性分析

引理 由文獻［12］中的結論知，當a≠0，b≠0時，若bc＜0，系統（1）只有一個平衡點O（0，0，0）；當bc≥0，系統（1）有3個平衡點且當a＞0，c＜0時，平衡點O漸近穩定；b≠0，ac＞0時，平衡點O不穩定；當bc＞0，a＞0，a＋b＞0，ab（a＋b－2c）＞0時，平衡點E1，E2漸近穩定；當bc＞0，ab時，系統在平衡點E1發生Hopf分岔，且

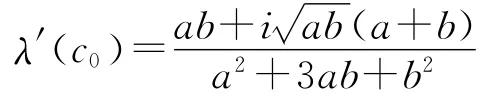
取c為分岔參數，由上面的結論知，當a＝7，b＝2，c＝c0＝4.5時，系統（1）在平衡點E1（3，3，4.5）和E2（－3，－3，4.5）處發生Hopf分岔，分岔位置如圖1所示，分岔圖如圖2～圖3所示。另外，從圖2和圖3可看出，系統（1）在E1和E2處的Hopf分岔方向均發生在臨界點右側。

1.2 Hopf分岔類型及周期解

首先，討論系統在平衡點E1處的分岔類型。經計算得α′（0）＝Re｛λ′（c0）｝＝0.147 4＞0，ω′（0）＝lm｛λ′（c0）｝＝0.354 5。做變換

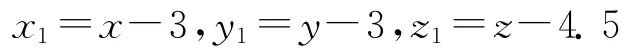
將平衡點E1移到原點。整理得

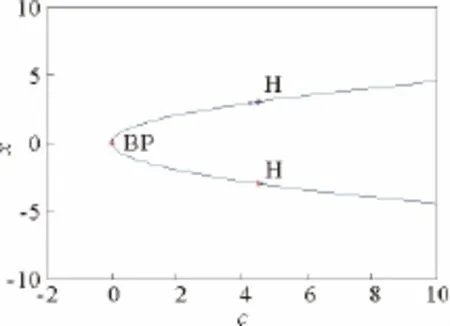
圖1 平衡點分岔位置圖Fig.1 Bifurcation position diagram near equilibrium

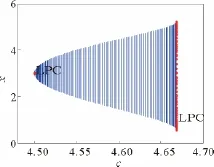
圖2 系統（1）在E1處的分岔圖Fig.2 Bifurcation diagram of system （1）for E1

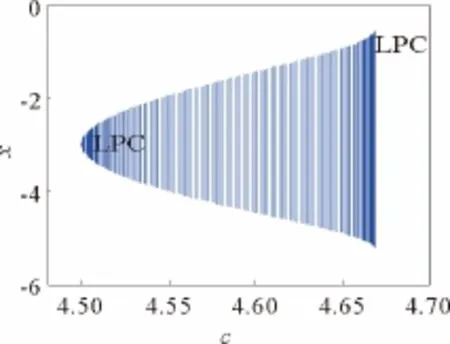
圖3 系統（1）在E2處的分岔圖Fig.3 Bifurcation diagram of system （1）for E2

則系統（2）的線性化矩陣為

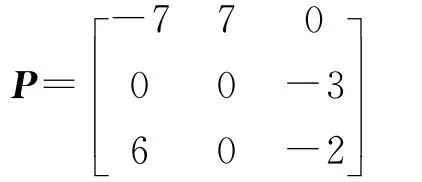
矩陣P有一對純虛特征根λ1，2＝±3.741 7i和一個負實根λ3＝－9，設α1，α3分別為特征值λ1＝＋3.741 7i和λ3＝－9對應的特征向量。通過計算得

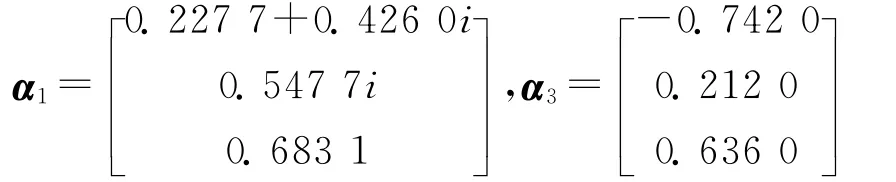
定義矩陣

作變換

系統（2）變為

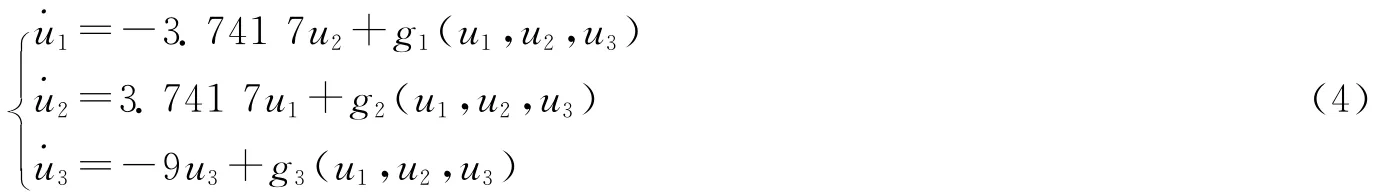
其中

由文獻［13］及上式計算得

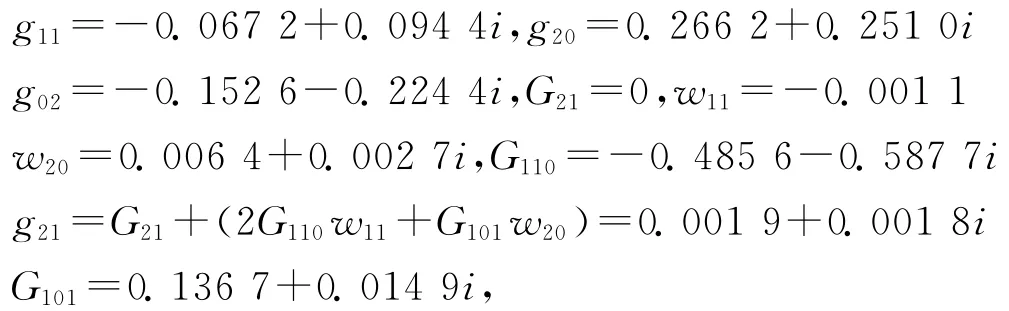
將上述結果代入式（5）

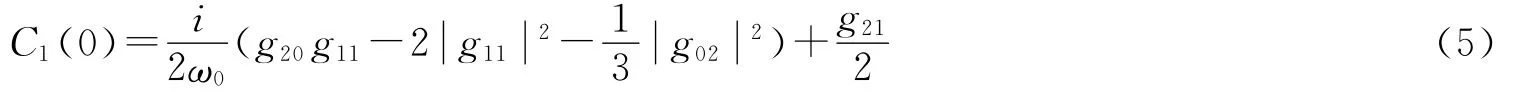
得到

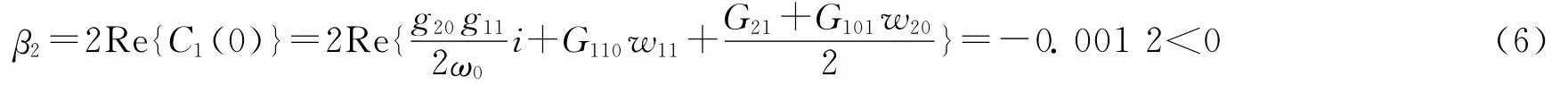
又因為α′（0）＝0.147 4＞0，由Hopf分岔理論知，系統（1）在分岔點E1處的分岔周期解是軌道漸近穩定的，產生與初始條件無關的穩定極限環，發生的Hopf分岔為超臨界分岔，分岔方向為c＞c0＝4.5，這點從圖2也可以看出。當c＜c0＝4.5且時，平衡點漸近穩定，如圖4所示；當c＞c0＝4.5且時，平衡點不穩定并在其附近產生穩定的極限環，如圖5所示。其中，仿真初值為（x0，y0，z0）＝（4.5，4.5，4.5）。

根據上面的計算結果，可以計算出重要特征向量

進一步得到系統的分岔周期解為

其中

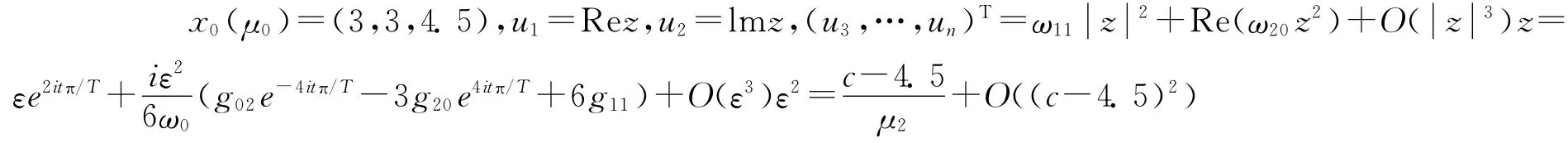
周期和特征性指數分別為

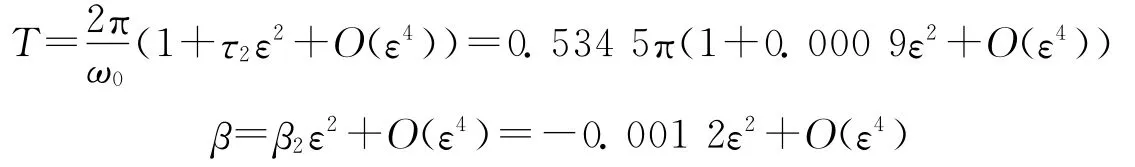
用同樣的方法可判斷系統（1）在平衡點E2處的分岔類型為超臨界Hopf分岔，系統受擾離開平衡點將產生等幅振蕩，在平衡點E2附近產生一個穩定的極限環，如圖6所示。

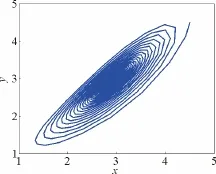
圖4 c＝4.2時，系統（1）在E1處的相圖Fig.4 Phase chart of system（1）at E1for c＝4.2

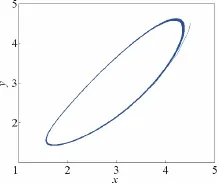
圖5 c＝4.6時，系統（1）的相圖Fig.5 Phase chart of system（1）at E1for c＝4.6

圖6 c＝4.6時，系統（1）在E2處的相圖Fig.6 Phase chart of system （1）at E2for c＝4.6

2 系統Hopf分岔控制

2.1 線性控制

不改變原系統的Hopf分岔點，采用線性控制器，對系統（1）作如式（8）的控制：

其中，k1，k2，k3為待定控制參數。當a＝7，b＝2，c＝4.5時，（x0，y0，z0）＝＝（3，3，4.5）。此時系統（8）變為

令

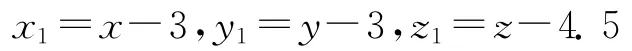
則系統（9）轉化為

系統（10）在平衡點（0，0，0）的穩定性情況相當于系統（9）在平衡點（3，3，4.5）的穩定性情況。系統（10）在平衡點（0，0，0）的線性化矩陣為

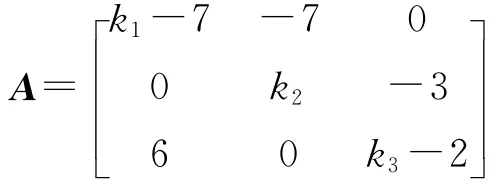
下面分3種情況討論線性控制對Hopf分岔位置的影響。為對結果進行比較，以下的仿真初值均選為（15，3.5，7.5）。

2.1.1 k2≠0，k1＝0，k3＝0時，受控系統 Hopf分岔分析

此時矩陣A對應特征方程為

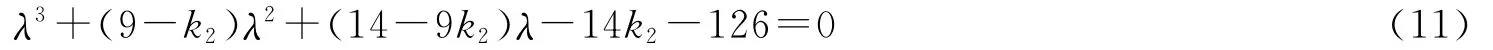
根據Routh－Hurwitz原理，方程所有的根具有負實部的充要條件是9－k2＞0，－14k2－126＞0，（9－k2）（14－9k2）＞－14k2－126。因此，當且僅當k2＜－9（k1＝0，k3＝0）時，方程所有根的實部為負數，在這個條件下，系統（10）的平衡點（0，0，0）是漸近穩定的。如取k2＝－10，k1＝0，k3＝0時，矩陣A對應特征根為λ1＝－0.138 1，λ2，3＝－9.431 0±3.528 8i。所有特征根具有負實部，系統（10）在平衡點（0，0，0）漸近穩定，進而得到系統（9）在平衡點（3，3，4.5）漸近穩定，故系統（1）在施加線性控制器后，Hopf分岔行為得到控制（見圖7）。這表明可以采用只在系統（8）的第2個方程中施加線性控制器的方法來抑制Hopf分岔的出現。但有時為了表明不同線性控制器參數對Hopf分岔位置影響的不同以及它們之間的相互影響，還可以在系統的其他方程中施加線性控制器，討論施加單個線性控制器和施加多個線性控制器對抑制Hopf分岔發生的不同影響。

2.1.2 k2＝－10，k1＝0，k3≠0時，受控系統 Hopf分岔分析

此時矩陣A對應特征方程為

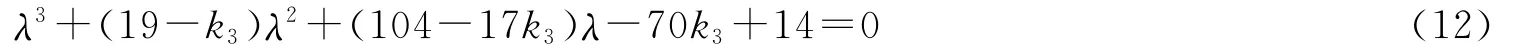
根據Routh－Hurwitz原理，當且僅當k3＜0.2（k2＝－10，k1＝0）時，方程所有根具有負實部，此時，系統（10）的平衡點（0，0，0）漸近穩定。如取k2＝－10，k1＝0，k3＝0.1，矩陣A 對應特征根為λ1＝－0.069 3，λ2，3＝－9.415 3±3.513 7i；如取k2＝－10，k1＝0，k3＝－8，矩陣A 對應特征根為λ1＝－3.762 0，λ2，3＝－11.619 0±4.192 6i。所有特征根具有負實部。所以，系統（10）在平衡點（0，0，0）漸近穩定，進一步說明原系統Hopf分岔行為得到控制（見圖8～9）。

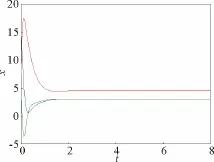
圖7 k2＝－10，k1＝0，k3＝0時，系統（8）波形圖Fig.7 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝0

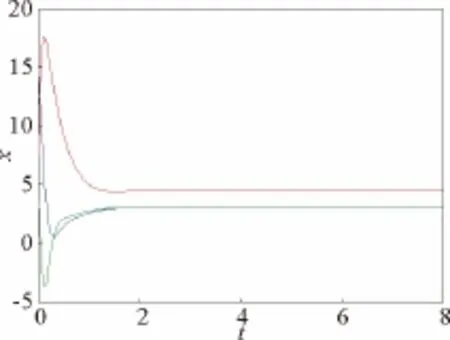
圖8 k2＝－10，k1＝0，k3＝0.1時，系統（8）波形圖Fig.8 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝0.1

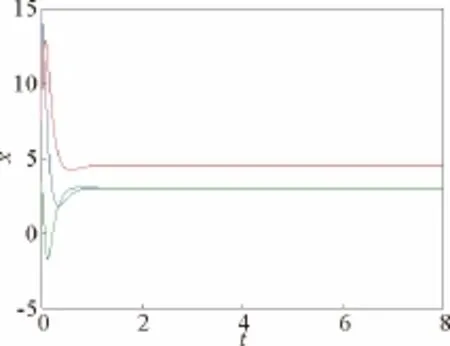
圖9 k2＝－10，k1＝0，k3＝－8時，系統（8）波形圖Fig.9 Waveform chart of system （8）for k2＝－10，k1＝0，k3＝－8

由圖8和圖9可知，當k1＝0，k2＝－10時，系統Hopf分岔點趨于穩定的速度隨著k3的減小而加快。由圖7和圖8知，施加雙線性反饋控制比單線性反饋控制的效果好，系統分岔點趨于穩定的速度更快。

2.1.3 k2＝－10，k1≠0，k3＝－8時，受控系統 Hopf分岔分析

此時矩陣A對應特征方程為

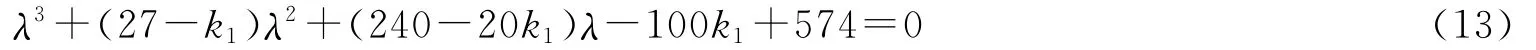
方程所有的根具有負實部的充要條件是k1＜5.74（k2＝－10，k3＝－8），在此條件下，系統（10）的平衡點（0，0，0）漸近穩定。如取k2＝－10，k1＝3，k3＝－8，矩陣A對應特征根為λ1＝－2.020 9，λ2，3＝－10.989 5±3.848 6i；如取k2＝－10，k1＝－9，k3＝－8時，矩陣A對應特征根為λ1＝－6.380 8，λ2，3＝－14.809 6±3.417 9i。所有特征根具有負實部，系統（10）在平衡點（0，0，0）漸近穩定（見圖10和圖11）。從圖10和圖11可看出，當k2，k3固定時，系統Hopf分岔點趨于穩定的速度隨著k1的減小而加快。

綜上可知，當線性控制參數滿足一定條件時，可抑制原系統Hopf分岔的發生，進而抑制混沌的出現。

2.2 極限環幅值控制

2.2.1 基于Normal Form方法的立方非線性反饋控制

不改變原系統的Hopf分岔點，對系統（1）施加如下非線性控制器：

因為系統在平衡點的穩定性主要由系統在平衡點的線性化矩陣對應特征方程的特征根性質來判定，又因為文中討論的平衡點是O（0，0，0），所以，影響系統在平衡點O的穩定性因素是系統的線性項部分，非線性項影響的是系統的非線性特性，比如周期解的穩定性情況及周期解幅值大小等。下面討論非線性控制器參數對極限環幅值的影響。

令

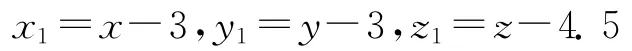
則系統（14）化為

其中，系統（15）的線性和非線性部分分別為

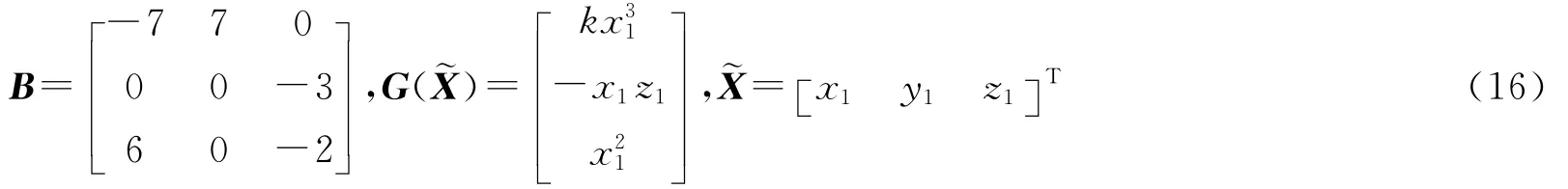
矩陣B有一對純虛特征根λ1，2＝±3.741 7i，相應的特征向量為φ，。其中

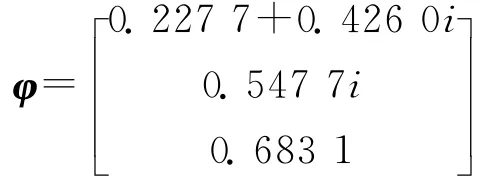
根據文獻［14］中提出的計算Normal Form的直接方法，引入變換：

即可求得方程的Hopf分岔Normal Form

其中，C ＝ 〈ψ，F21〉，ψ 滿足（BT－3.7417iI）ψ ＝0，〈ψ，φ〉＝1，

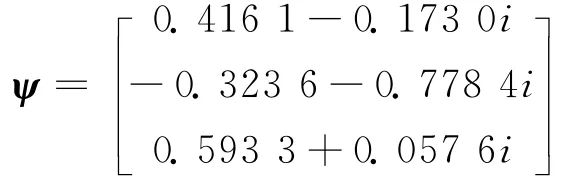
將非線性變換（17）代入非線性項中整理成關于u，uˉ的多項式形式

其中，F21為u2對應的系數向量。

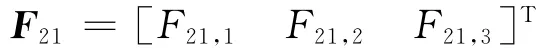
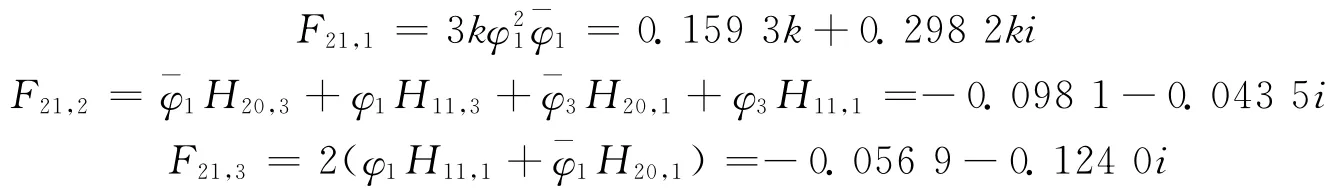
上式中，Hjk，m為向量Hjk中的第m 個元素。其中

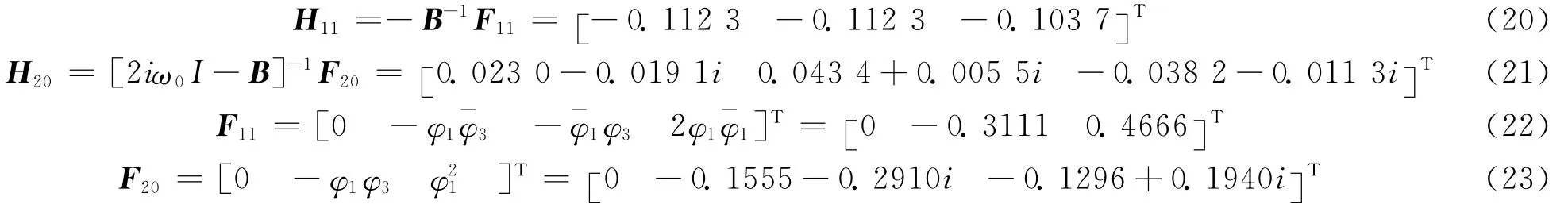
由式（20）～ （23）計算C得

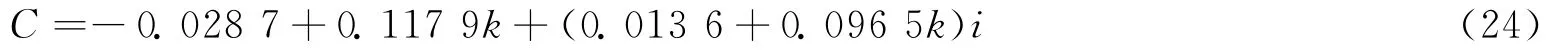
所以，式（14）的Normal Form為

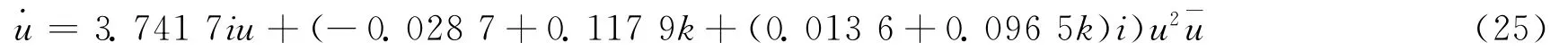
2.2.2 仿真研究

由 Hopf分岔理論知，當k＜0.243 4時，Re（C）＜0，又因為α′（0）＝0.147 4＞0，所以，系統（14）的 Hopf分岔類型為超臨界分岔且Hopf分岔方向為c＞c0＝4.5，極限環穩定，極限環的幅控關系為

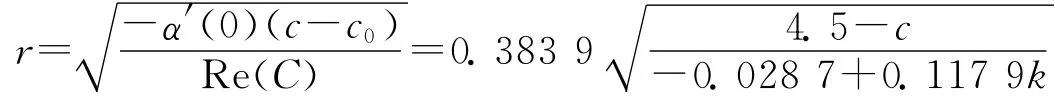
如圖12所示，極限環幅值r與控制系數k是增函數關系。另外從圖13和圖14也可看出，振動幅值（極限環幅值）隨著k的減小而減小。并且，k的范圍恰好包含了k＝0的情況，與原系統的分岔類型相對應。其中，仿真初值為（x0，y0，z0）＝（4.5，4.5，4.5）。

當Re（C）＞0，即k＞0.243 4時，系統（14）的Hopf分岔類型為亞臨界分岔，極限環不穩定（見圖15）。

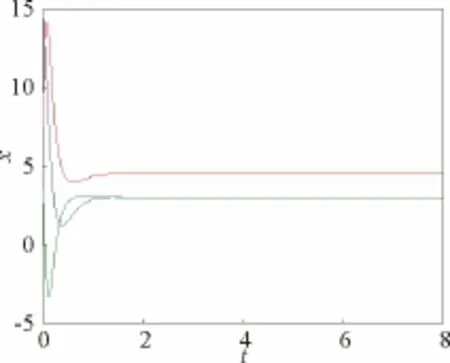
圖10 k2＝－10，k1＝3，k3＝－8時，系統（8）波形圖Fig.10 Waveform chart of system （8）for k2＝－10，k1＝3，k3＝－8

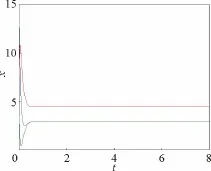
圖11 k2＝－10，k1＝－9，k3＝－8時，系統（8）波形圖Fig.11 Waveform chart of system （8）for k2＝－10，k1＝－9，k3＝－8

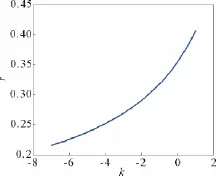
圖12 受控系統（14）的限極環幅值曲線（c＝4.6）Fig.12 Gain amplitude curves for the controlled system （14）（with c＝4.6）

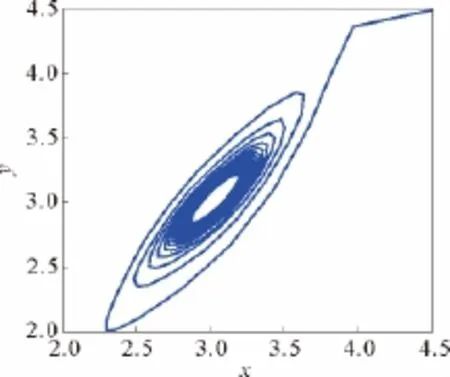
圖14 c＝4.6，k＝－5時，系統（14）波形圖Fig.14 Phase chart of system （14）with c＝4.6，k＝－5

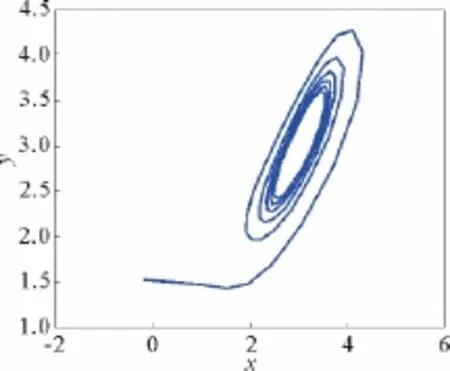
圖15 c＝4.6，k＝1.2時，系統（14）相圖Fig.15 Phase chart of system （14）for c＝4.6，k＝1.2

由以上分析知，當非線性控制參數滿足一定條件時，可以改變原系統的分岔類型和分岔周期解振幅大小，從而實現類Lorenz系統的極限環幅值控制。

3 結論

本文主要研究了一個新的類Lorenz系統的Hopf分岔行為和分岔控制問題。首先，通過規范形方法計算出系統的穩定性指標，進而判定系統的Hopf分岔類型；然后，對系統分別施加線性和非線性控制器，并詳細討論了線性控制器和非線性控制器對Hopf分岔位置、分岔類型和分岔周期解幅值（極限環幅值）的影響，進而實現類Lorenz系統的分岔控制問題。

［1］ Lorenz E N.Deterministic non－periodic flows［J］.J Atmos Sci，1963，20：130－141.

［2］ Tucker W.The Lorenz attractor exists［J］.C R Acad Sci Pairis，1999，328：1197－1202.

［3］Stewart I.The Lorenz attractor exists［J］.Nature，2002，406：948－949.

［4］ Pang S Q，Liu Y J.A new hyperchaotic system from the Lüsystem and its control［J］.Journal of Computational and Applied Mathematics，2011，235（8）：2775－2789.

［5］ Mahmoud E E.Dynamics and synchronization of new hyperchaotic complex Lorenz system［J］.Mathematical and Computer Modelling，2012，55（7／8）：1951－1962.

［6］ Niu Y J，Wang X Y.A new hyperchaotic system and its circuit implementation［J］.Commun Nonlinear Sci Numer Simulat，2010，15（11）：3518－3524.

［7］ Mkaouar H，Boubaker O.Chaos synchronization for master slave piecewise linear systems：application to Chua′s circuit［J］.Commun Nonlinear Sci Numer Simulat，2012，17（3）：1292－1302.

［8］Sprott J C.Some simple chaotic flows［J］.Physical Review E，1994，50（2）：647－650.

［9］ 魏周超，楊啟貴.基于Lorenz型系統族的三維系統的復雜動力學研究［D］.廣州：華南理工大學，2011.Wei Zhouchao，Yang Qigui.Research on complicated dynamics of three－dimensional systems based on a family of Lorenz－type systems［D］.Guangzhou：South China University of Thecnology，2011.

［10］Yang Q G，Chen G R.A chaotic system with one saddle and two stable node－foci［J］.Int J Bifurc Chaos，2008，18（5）：1393－1414.

［11］李春來，禹思敏.一個新的超混沌系統及其自適應追蹤控制［J］.物理學報，2012，61（4）：1－7.Li Chunlai，Yu Simin.A new hyperchaotic system and its adaptive tracking control［J］.Acta Phys Sin，2012，61（4）：1－7.

［12］李群宏，徐德貴.一個類Lorenz系統的動力學分析［J］.重慶理工大學學報，2011，25（2）：112－116.Li Qunhong，Xu Degui.Dynamics analysis of a Lorenz－like system［J］.Journal of Chongqing University of Technology，2011，25（2）：112－116.

［13］Hassard B D.Theory and Application of Hopf Bifurcation［M］.New York：Cambridge University，1981.

［14］吳志強，孫立明.基于washout濾波器的R¨ossler系統 Hopf分岔控制［J］.物理學報，2011，60（5）：1－5.Wu Zhiqiang，Sun Liming.Hopf bifurcation control of the R¨ossler system based on washout filter controller［J］.Acta Physical Sinica，2011，60（5）：1－5.