基于數據鏈的空戰對抗建模及增援決策分析

牛德智，陳長興*，徐浩翔，李永賓，王卓，陳強

(1.空軍工程大學 理學院，西安710051;2.空軍工程大學 裝備管理與安全工程學院，西安710051)

在信息化戰爭條件下，航空武器系統越來越倚靠于高效可靠的通信手段來保障其性能發揮.數據鏈的出現，實現了戰場態勢共享、精確指揮控制和武器協同打擊的無縫鏈接［1－2］，成為武器裝備的生命線.另外，衡量航空武器系統整體的作戰效能［3－5］，對于科學研判和有效分析系統的整體性能，具有重要的現實意義.從系統融合的角度出發［6］，將效能評估和作戰應用銜接起來構成環路，是研究現代空戰規律的必然要求，掌握空戰變化的內部規律，無疑會使得整個空戰的安排部署和指揮決策更加合理和高效.

在現有針對航空作戰的研究中，主要集中在兩方面［7－9］:一種是不同想定場景不同衍化規律下的作戰雙方數量變化情況，這種研究一般戰場信息交互作用(數據鏈)考慮得少，也未針對不同武器系統的作戰效能如何體現;另一種是停留在僅從頂層設計作戰流程或過程的框架結構上，考慮的因素和方面很廣但是難以有效聚合起來，形成量化或程式的部署和決策準則.對于航空作戰這樣一個體系復雜的系統過程，需要通過全要素分析形成具有相互關聯的輸入輸出網絡關系，從而將“作戰—評估—運用”的環路有效連接起來，以期實現作戰效果的最優化.文獻［10］用多目標整數規劃的方法研究了數據包絡分析(DEA)效能評估中的權重問題，但是該方法實現起來具有一定的時間復雜度，且權重法獲得的效能本身主觀性就較大.文獻［11］分析了數據鏈對發現概率、擊毀概率的影響，并將這種影響體現到雙方參戰或退出戰斗飛機的數量中來，這實現了數據鏈與作戰過程的聯系，但是它主要側重于從不同作戰單元的打擊概率等描述整體的作戰能力，未能給出整個戰斗過程的兵力變化規律.文獻［12］考慮信息因素對作戰的影響，在藍徹斯特方程中引入了具有交互功能的戰場感知系數，進而將其作用到交戰過程中的兵力變化，具有一定的借鑒意義，但是未能結合不同對象的作戰效能大小進行研究.在藍徹斯特方程運用方面，文獻［13］研究了基于藍徹斯特方程的兵力增援優化控制問題，文獻［14］利用藍徹斯特方程和微分對策研究了最優火力分配的優化對策問題，給出了作戰對策的最優性條件和求解方法.

本文的出發點在作戰環路內討論雙方力量構成的變化規律.通過將效能評估的結果轉化為表征作戰效率的平均戰斗力水平，據此建立兵力變化數學模型，并主要對不同增援模式下的戰斗結果進行分析評價，確定了實際中應采用的增援作戰形式.

1 飛機作戰效能

在對作戰飛機進行效能評估時，可以采用計算空戰能力指數的方法來衡量.該方法選用有關空戰的7個主要項目來衡量飛機的空對空作戰能力［15］，并將空戰能力指數表示為

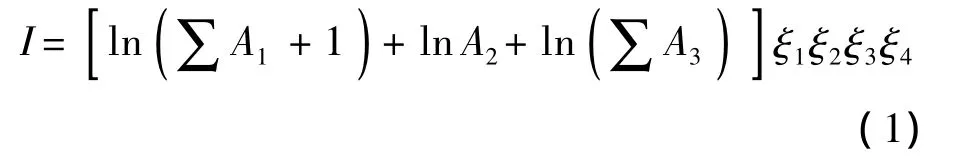
其中，I為空戰能力指數;A1～A3分別為火力、機動性、探測目標能力參數;ξ1～ξ4分別為生存力、電子對抗能力、航程、飛行員操縱效能系數.空戰能力指數一般遠大于1.空戰能力指數定量體現了戰機的作戰能力，在針對空戰對抗建模時需要將其轉化成單機對單機的毀傷效率(或毀傷能力)，這就是平均戰斗力水平.

為此，作如式(2)的變換，將空戰能力指數I變換為在區間(0，1)上的平均戰斗力水平γ(其中k為一正比例調節因子，引入它是防止變換所得的γ在數值上過于集中).

此處說明，γ的物理意義就是空戰對抗時我方單機對敵方單機(或敵方單機對我方單機)的毀傷效率.容易證明γ和I具有變化的一致性，即γ在保證空戰能力指數特性的情況下，可以用來作為平均戰斗力水平.

2 空戰力量對比的建模分析

2.1 數據鏈體制下的動態力量變化微分模型

在對作戰兵力變化規律的研究中，藍徹斯特方程［16］可以反映兵力編成和裝備特性因素的變化結果，適用于多種類型作戰模擬.本文的分析將以藍徹斯特方程為基礎，并以此對不同場景下的兵力變化過程進行建模及仿真.此處給出藍徹斯特平方律方程的表達式為

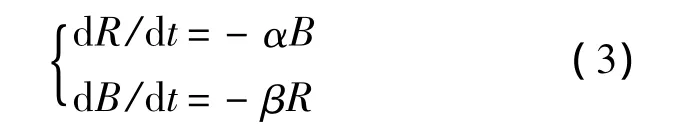
式中，R和B分別為紅、藍軍在時刻t的戰機數量;α和β分別為藍、紅軍每個戰機的平均戰斗力水平，其求解可通過式(1)～式(2)來實現.用式(3)描述的模型為雙方均采用單一機型對抗時的雙方數量變化情況，若雙方作戰投入的是不同數量的多機型戰機，則相應的雙方數量變化模型為

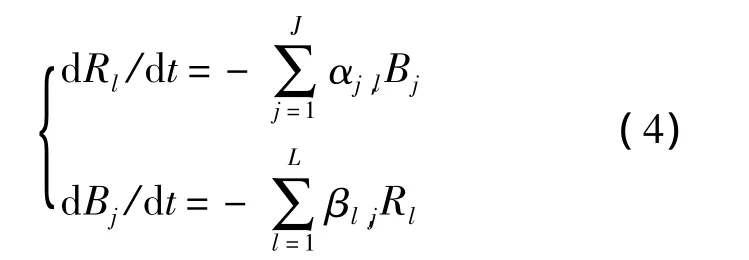
該模型中，藍、紅軍分別投入J種、L種機型，相應的Bj和Rl表示不同機型的數量;αj，l表示藍軍第j種機型對紅軍第l種機型的平均戰斗力水平;βl，j的意義類似.需要說明的是，多機型對抗時，每種機型對敵方的某一機型的空戰能力指數I都是不同的，因為I受7個不同參數的控制，而這些參數都是與參與作戰的雙方機型相關的，這樣就會有不同的平均戰斗力水平 αj，l和 βl，j.

在實際中，若要對多機型的情況進行分析，則應在式(4)的基礎上進行相關公式的變化.在下文中，為了說明空戰對抗的建模方法及求解過程，以及說明不同增援模式的性能優劣結論，仍以雙方為單機型對抗的情況進行分析.對式(3)求其狀態解可得(B0和R0分別表示雙方的初始數量):

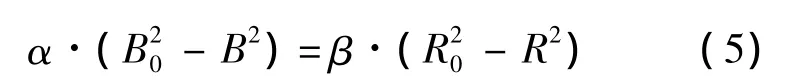
考慮紅軍(或藍軍)裝備數據鏈時的雙方對抗中的戰機數量變化情況.數據鏈由于具有態勢共享和武器協同等優勢，可以顯著提高飛機的空戰能力，所以在考慮數據鏈時若其對紅軍戰斗力水平的提升率為λ，則紅軍的平均戰斗力水平變為β(1+λ)，對于未裝備數據鏈的藍軍，其戰機的平均戰斗力水平改變為α(1－λ)，于是可建立數據鏈體制下雙方力量動態變化的數學模型為

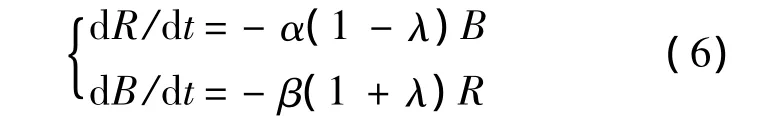
若雙方均采用數據鏈，需定義相對提升率并將其運用到上式中，給出相對提升率為

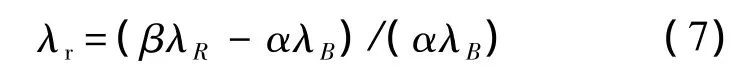
由該定義式可知，λr可正可負，為正時雙方數據鏈的綜合作用是紅軍戰斗力水平得到提高，反之為負時藍軍得到提高.事實上，引入數據鏈的戰機，由于具有了態勢共享功能，在某種程度上說它可使戰機具有先敵發現和遠距離打擊的優勢.對應到空戰能力指數的相關參數中，其可以影響探測目標能力和電子對抗能力等［17－18］，進而提升戰機的空戰能力.數據鏈對戰機作戰能力的影響，體現到模型中就是其影響了平均戰斗力水平，故本文采用一個對平均戰斗力具有綜合作用的提升率修改空戰對抗的數學模型，該提升率的大小與雷達搜索方位角、雷達探測距離、協同作戰時的機間距離等因素有關.

進一步，在有增援時，可建立該情形下的空戰模型為

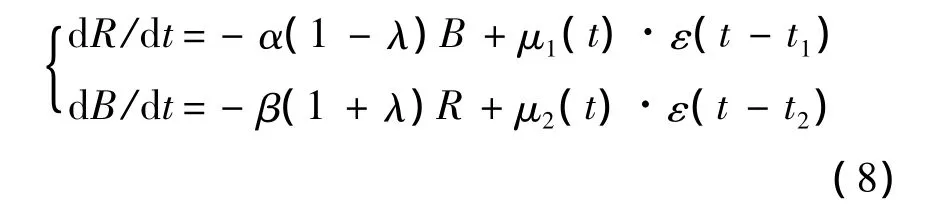
式中，μ1(t)和μ2(t)為雙方的增援率;t1和t2為增援開始的時刻;ε(t)為階躍函數，用它來表示只有當增援時間開始時，增援力量才能加入.

2.2 模型離散化和數值計算方法

借助相關軟件求解微分方程組的方法不易分析變量的變化規律，尤其本文考慮增援的情況下不易在求解中體現不同增援時刻的影響，故應設計合理的數值求解方法.將式(3)中的第1個方程進行離散處理，得其差分形式為

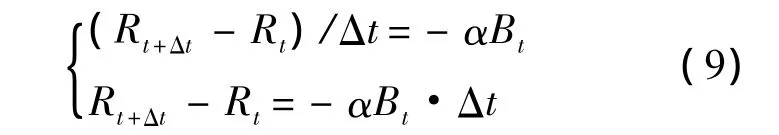
在式(9)中，Δt為一較小的時間步長，其選取原則是，可維持原微分方程中變量的變化規律.在對時間進行離散化處理時，依次令 t=0，Δt，2Δt，…，nΔt(n表示總戰斗回合數，即每個戰斗回合雙方均有對抗攻擊，但該回合內并不能完全摧毀對方)，并記 RnΔt為 Rn，則式(9)化為

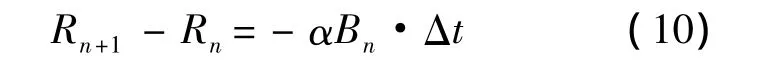
接下來，需確定如何選取合適的 Δt.文獻［12］中也對藍徹斯特方程進行了差分處理，但其實質是直接令Δt=1，這樣處理獲得的數據具有片面性，并未能完全體現出變量的變化規律，也不利于通過數據變化研究作戰規律.為此，寫出式(10)的完整形式:

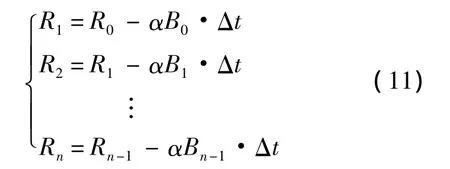
將上式中的n個等式進行相加，得

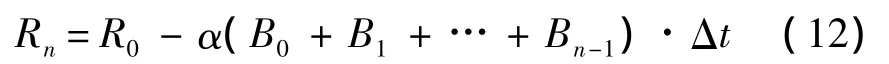
若考慮藍軍失敗，則 Bn－1=0，這樣可將 Bn－1的變化規律近似用等差數列來描述，相應的式(12)簡化為

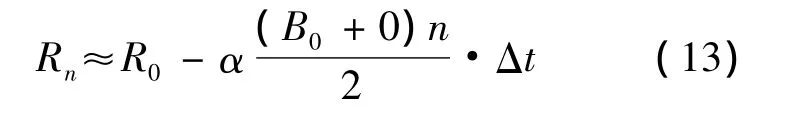
由上式可求

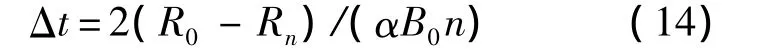
在式(5)中，若藍軍失敗則有B=0，于是

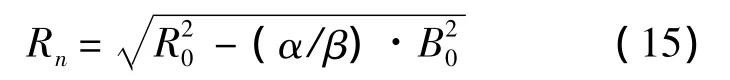
這樣綜合式(14)和式(15)就可以求得時間步長Δt(實際計算時所取的時間步長應小于或等于該值).另外，若紅軍失敗，則相應的時間步長為

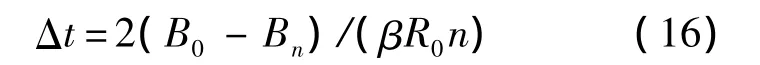
得到Δt后，則與模型式(6)對應的離散模型為

若考慮增援以上模型需修改為

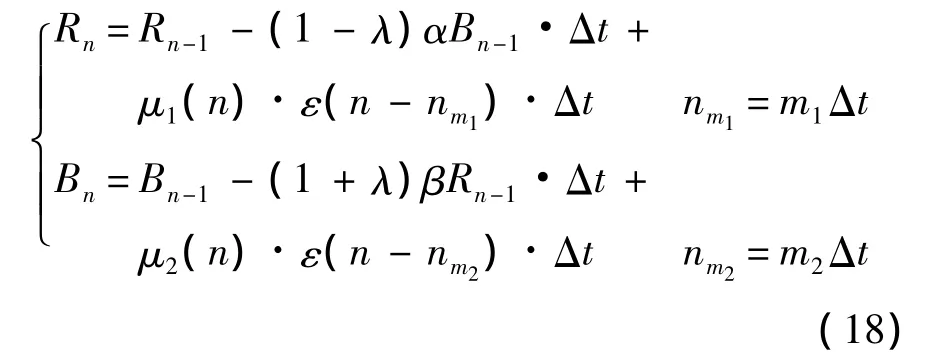
式中 m1，m2=0，1，2，…為整數，表示增援開始時刻.戰斗結束時(n=N)獲勝方(如紅軍)共增援飛機數為 Rs=μ1·Δt·(N －nm1+1)，損失數為Rd=R0+Rs－RN.

2.3 增援作戰時的模型分類

為了研究不同增援模式對空戰雙方兵力變化及戰斗結果的影響，考慮具有恒定和變化增援率的戰斗力量加入到雙方對抗的數學模型中，研究的目的在于給出在有限增援數量(可采取恒定或變化增援率的方案對作戰主體進行增援)或者增援數量不足需要補充增援(以變化增援率的方案對作戰主體進行增援，又可將其分為勻加速增援和勻減速增援)的情況下，哪種增援方式能夠使得獲勝方損失的戰斗數量少，同時所要求的增援總數不是很多.這樣，給出3種增援模式(勻速、勻加速、勻減速)下增援數量的變化規律為

式中，c為勻速增援的速率;c1和c2分別為變速增援時的起始速率.考慮勻速增援的總數為F，持續時間為 t，則，可得t=F/c.若在勻加速增援時維持相同的增援時間和總數，并且保持增援速率v一定，則可由求得初始時刻的增援速率為c1=(2F－vt2)/(2t).類似地，可由求得c2=(2F+vt2)/(2t).

在確定了勻加速和勻減速的初始增援速率值以后，3種增援模式的離散變化規律可以表示成

為簡化問題起見，僅考慮紅軍有增援的情形，將式(20)代入到式(18)中，可得具有變速率增援的雙方力量動態變化模型為

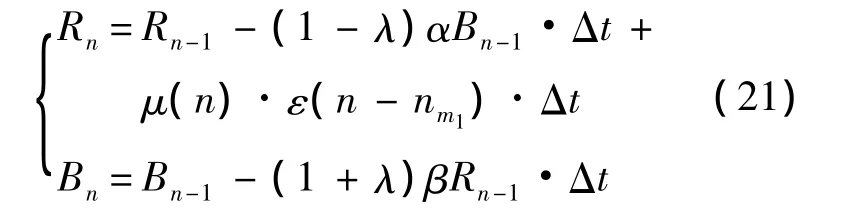
在式(5)、式(15)和式(21)中，考慮的都是增援一旦實施，就維持到戰斗結束直至一方獲勝.特別地，考慮勻速增援時的兩種特例，即勻速率增援至某一時間后停止增援、一次性增援一定數量的飛機后不再增援，其相應的數學模型如下.

勻速增援維持一段時間:

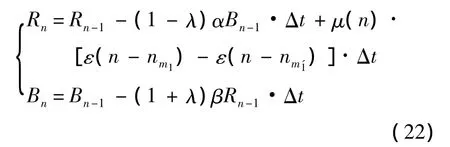
上式表示的含義為增援在［nm1，nm′1］(即時間范圍為［m1Δt，m′1Δt］)內起作用.

一次性增援:

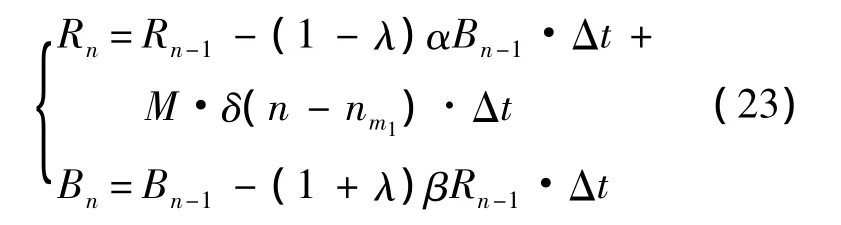
其中δ(n)表示沖激函數，用來說明一次性增援量M只在nm1時刻加入.

3 仿真實驗分析

設定參數為:紅、藍軍所用的機型為F－14A和F－15E，數量分別為10和15架.此處機型的選取只是為了將本文所建模型加以運用，并按照一組選定的機型作戰給出不同增援方式的優劣結論，所以并未選擇具有實際對立方或假想敵之間所采用的機型，如美制和俄制戰機等，若多機型對抗時則采用相應的多機型戰機數量變化模型進行仿真，特此說明.根據式(1)可計算得二者的空戰能力指數為13.4和19.8(文獻［17］)，采用本文的平均戰斗力水平轉化方法，分別求得β=0.58和α=0.7(取k為1/10).該組參數下紅軍的整體實力較弱，考慮其引入數據鏈會使平均戰斗力水平提升25%，即λ=0.25.如前文所述，λ的數值與雷達搜索方位角、探測距離以及協同作戰時的機間距離等有關，若結合“數據鏈為武器效能倍增器”的性能描述，則取λ=0.33較為合適，因為此時(1+λ)/(1－λ)=2，即戰斗力提高1倍.另外在文獻［17］所做的仿真實驗中也指出，使用數據鏈一方相比未使用數據鏈一方的戰斗力強出約30%.在這些參數下研究雙方作戰的力量變化較為符合實際，但是經本文算例實驗得知，若λ較大時，會造成不同情況下雙方兵力數量變化的曲線維持時間較短，也不利于描述不同情況下的曲線性能差別所在，故文中設定了λ=0.25.

3.1 勻速增援時不同起始時間下的動態損耗關系

設定c=2.0.為使模型演化過程中的數據變化符合連續系統微分方程中的規律，以式(16)求解的離散時間間隔為上限約束，取離散計算仿真時的 Δt=0.025.通過式(9)、式(17)和式(18)，仿真3種條件(原始實力下雙方作戰、紅軍僅引入數據鏈雙方作戰、紅軍同時擁有數據鏈和勻速增援力量雙方作戰)下雙方的動態損耗(動態變化)如圖1所示.

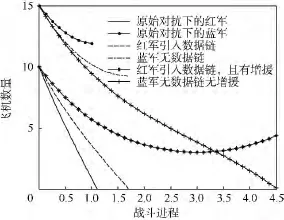
圖1 3種狀態下的雙方動態損耗Fig.1 Dynamic exhaustion under three statuses

圖1的縱坐標表示飛機數量，橫坐標描述的戰斗進程表示廣義的時間單位(僅表示時間的數字大小)，實際時間大小在微分方程模型中的時間量度給定以后可確定，在下文的仿真圖像中亦如此.由圖可知，原條件下的紅軍實力較弱最后失敗(數量為0即失敗).在引入數據鏈后，戰斗進程延長，紅軍在得到增援力量后取得戰斗勝利.

進一步討論勻速增援時紅軍有效的增援時間范圍.分別取m1=0，6和12，可得雙方兵力變化的動態損耗曲線如圖2所示.

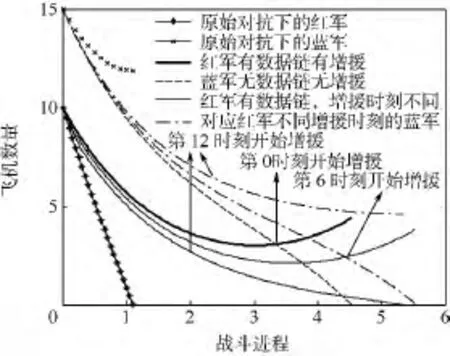
圖2 紅軍不同增援時刻時雙方的動態損耗圖Fig.2 Dynamic exhaustion in different reinforcement time from Red

可以看出當m1=12時，增援太晚紅軍仍為失敗(飛機數為0時不再增援).由此可知，勻速增援時存在一個時間分界點，在此之前實施增援，可改變戰局;反之不能.在文中仿真參數下，最終得到有效增援起始的時刻范圍為［0，11］.在該范圍內，讓m1按步進量為1進行取值，其他參數保持不變，可得雙方動態損耗曲線如圖3所示.

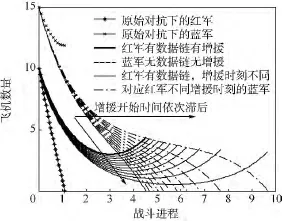
圖3 有效增援起始范圍內不同時刻時的動態損耗Fig.3 Dynamic exhaustion at different time among effective reinforcement beginning range

由圖3可知，增援實施時間越晚，空戰進程時間越長，紅軍勝利時剩余的飛機數越少.這說明，一定速率下的勻速增援，實施時間越早獲勝時的剩余戰斗數量越多.

3.2 3種勻速增援狀態時的動態損耗關系

設定的3種勻速增援狀態分別為:從0時刻(m1=0)開始一直勻速增援至勝利，從0時刻勻速增援至時刻m′1，在0時刻一次性增援M數量(勻速增援的特例)的飛機加入戰斗.參數設置仍同本節開始時的參數.通過仿真實驗可以確定，在一段時間勻速增援時保證紅軍獲得勝利的最小時刻為m′1=130，同樣的保證紅軍獲勝的一次性增援數量最小值M=4.繪制原始狀態下作戰和3種勻速增援模式時的動態損耗曲線如圖4所示.

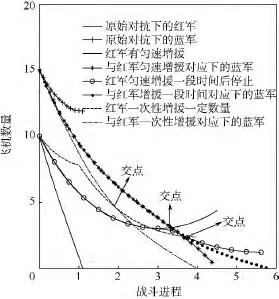
圖4 3種勻速增援模式時的動態損耗關系Fig.4 Dynamic exhaustion curve of three constant velocity reinforcement mode

分析圖4中的規律可知，一次性增援方案可以使得戰斗結束時間提前，一段時間區間上的勻速增援方案戰斗結束時間最晚，且獲勝時剩余飛機數量最少.

3.3 變速增援時的動態損耗關系

設定式(20)中的v=0.5，由前面實驗的仿真結果知，對于從0時刻開始增援直至戰斗勝利的勻速增援模式，有t=4.525，F=9.1，據此計算得到c1=0.8798，c2=3.1423.仿真時發現，在c1和v的取值下，勻加速增援模式并未能保證紅軍最后贏得勝利，在經歷時間為3.35后紅軍失敗.為了便于在同樣的v值下與勻減速增援模式進行方案比較，將 c1值調節為 c′1.具體做法是在 c1=(2F －vt2)/(2t)中，令 t=3.35 重新計算有，c′1=1.87.這樣，仿真出變速增援模式下雙方的動態損耗關系如圖5所示.

對于勻加速增援而言，若受v值限定，在與勻速增援持續相同的時間范圍內選定初始增援率值，并不能保證增援獲勝.在調節初始增援速率的條件下，勻加速增援可以縮短戰斗進程，并且使得最后獲勝方剩余戰斗力較多.對于勻減速增援而言，在持續增援時間小于勻速增援的時間下就可以獲得勝利(初始增援率值按照勻速增援維持的時間進行計算求得)，這說明勻減速增援在保證獲勝的情況下，其本身就具有很大的可調節性，且可以縮短戰斗進程和保持較大的剩余戰斗力.

根據以上仿真實驗可以得出結論，一次性增援和勻減速增援模式下可以保證獲勝的前提下，明顯地加快戰斗結束進程.至于每一種增援模式下的增援效率(即由增援數量和損失數量的多少來判定增援方案的優劣)，下面將重點予以討論.

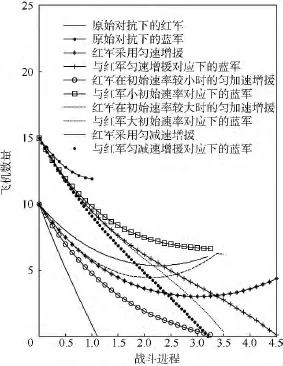
圖5 變速增援模式時的雙方動態損耗Fig.5 Dynamic exhaustion curve of varied velocity reinforcement mode

4 增援方式優劣的評判準則制定

分析增援作戰的要求可知，對增援飛機的數量要求不能很多(即增援飛機的規模，因為兵力總是有限的)，另一方面，總是希望戰斗至獲勝時損失掉的飛機數量要少.若以ρ來表示增援效率因子，ρ值越大表示增援方案越優，則ρ∝1/Rs，且同時應有ρ∝1/Rd，這兩個條件有效表征了增援作戰的投入規模與付出代價對增援效率的影響.另外，考慮在投入規模與付出代價乘積相同的情況下，損失飛機數量越少的增援方案越優，為此，需要給損失飛機與增援效率之間比例關系引入一個表示權重大小的值ω(Rd).為簡單起見，本文取權值為ω(Rd)=1/Rd.這樣，構造出衡量增援方案優劣的“評價函數”為

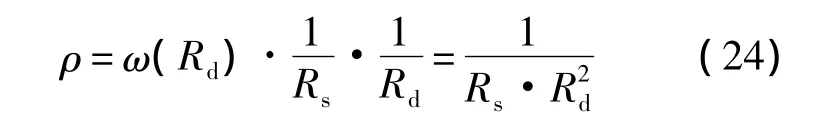
這樣，記錄以上實驗中得到的紅軍不同類別的飛機數量并計算增援效率，據此對不同增援模式的優劣性進行評價，如表1所示.

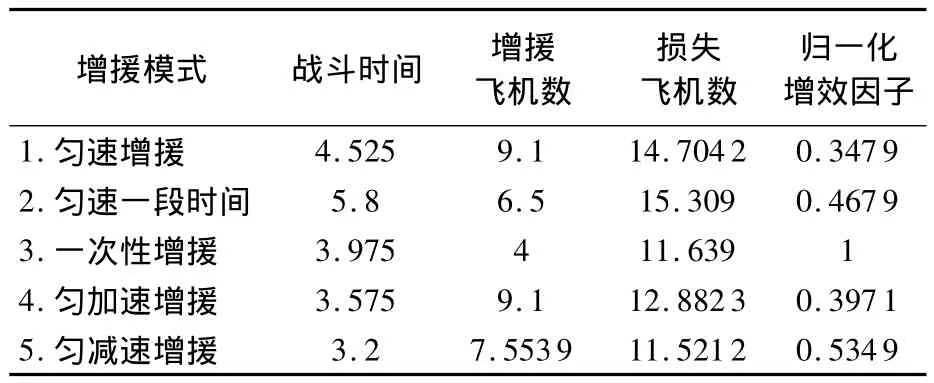
表1 不同增援模式的增援效率(R0=10)Table1 Kinds of data in different reinforcement mode

表1中的戰斗時間僅表示數字意義上的時間大小(無量綱)，其實際時間取決于微分方程中的時間量度(3.1節中也有說明).表1中歸一化增效因子的計算公式為

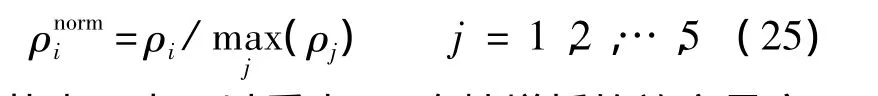
從表1中可以看出，一次性增援的效率最高，勻減速增援的效率次之，且這兩種增援模式均可以加快紅軍獲勝的戰斗進程，這與上節中關于時間效率的實驗結果是一致的.圖6也給出了不同增援模式的增援效率變化規律，從中也可以更明顯地看出增效高低的增援方案.

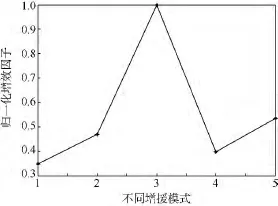
圖6 不同增援模式時的增援效率Fig.6 Reinforcement efficiency in different reinforcement mode

本文的實驗結果說明，在增援作戰時，若增援規模許可的條件下，一次性投入一定兵力的增援模式效率最高;若增援規模受限，可在滿足條件的情況下采用勻減速增援方案，這樣也可獲得較高的增援效率和較短的戰斗維持時間.

5 結論

1)建立了空中對抗作戰的數學模型，指出了離散計算的時間步長所應滿足的條件.將戰機效能評估的結果(平均戰斗力水平)作為其毀傷效率，并考慮在數據鏈環境下的平均戰斗力水平的相對變化情況，建立表示雙方作戰單位數量變化的微分方程模型.為便于仿真實現和研究戰斗變化規律，給出了所建模型的數學求解方法.

2)給出了不同增援方式的優劣結論.在不同增援方式的空戰對抗數學模型中，進行了3種不同情形下的空戰對抗實驗，分別是勻速增援時起始時間不同的雙方動態損耗實驗、3種不同類型勻速增援的雙方動態損耗實驗、變速增援的雙方動態損耗實驗.在第1種實驗中得出結論為增援時間越早，損失的戰機數量越少.在后2種實驗中，通過構造增援效率評價函數進行有效度量，得出結論為一次性增援和勻減速增援方案的性能較優.實驗結論為空戰指揮和決策提供了依據.

下一步的研究中，將對雙方均采用多機型的對抗情況進行深入研究，該情形下的增援決策問題將會是一個復雜的多目標求解與優化問題.

References)

［1］ Zhou L，Zhang H Y，Wang T，et al.Static check of WS－CDL documents［J］.IEEE International Symposium on Service－Oriented System Engineering，2008，8:142－147.

［2］ 賀剛，柏鵬，彭衛東，等.數據鏈中基于動態博弈的聯合功率與速率控制［J］.西南交通大學學報，2013，48(3):473－480.He G，Bai P，Peng W D，et al.Joint rate and power control based on dynamic game theory in data link system［J］.Journal of Southwest Jiaotong University，2013，48(3):473－480(in Chinese).

［3］ 魏嘉利，賈云峰，謝樹果，等.航空電子系統電磁環境復雜度量化評估方法［J］.航空學報，2014，35(2):487－496.Wei J L，Jia Y F，Xie S G，et al.Complexity assessment method of electromagnetic environment for avionic systems［J］.Acta Aeronautica et Astronautica Sinica，2014，35(2):487－496(in Chinese).

［4］ 林琪，李智.基于拓撲特征的衛星網絡效能評估［J］.中南大學學報:自然科學版，2013，44(增刊 2):368－371.Lin Q，Li Z.Performance evaluation of satellite－network based on topologic characteristics［J］.Journal of Central South University:Science and Technology，2013，44(S2):368－371(in Chinese).

［5］ Liu H，Xu M，Chen N Y，et al.Task effectiveness evaluation on anti－ship attack of fighter aircraft［J］.Transactions of Nanjing U－niversity of Aeronautics ＆ Astronautics，2012，29(2):164－170.

［6］ Lee J，Kang S H，Rosenberger J，et al.A hybrid approach of goal programming for weapon systems selection［J］.Computers ＆ Industrial Engineering，2010，58(3):521－527.

［7］ Chen J，Mu Y P，Li D F.Study on effect evaluation of weapon coordinated use of fleet［J］.Military Operations Research and Systems Engineering，2009，23(3):66－71.

［8］ Johnson I R，Mackay N J.Lanchester models and the battle of Britain［J］.Naval Research Logistics，2011，58(3):210－222.

［9］ Yan J J，Wang Y，Wang X Y.Modeling and simulation of Lanchester equation based on game theory［C］//Proceedings of International Conference on the Business Management and Electronic Information.New York:IEEE，2011:212－214.

［10］ Yang F，Yang C C，Liang L，et al.New approach to determine common weights in DEA efficiency evaluation model［J］.Journal of Systems Engineering and Electronics，2010，21(4):609－615.

［11］ 馮忠華，王新龍，王彬.一種數據鏈傳輸延遲建模及其補償方法［J］.北京航空航天大學學報，2012，38(8):1106－1110.Feng Z H，Wang X L，Wang B.Transfer time delay model of data link and its compensation［J］.Journal of Beijing University of Aeronautics and Astronautics，2012，38(8):1106－1110(in Chinese).

［12］ 陳向勇，井元偉，李春吉.基于Lanchester方程的作戰混合動態系統最優變招控制［J］.控制理論與應用，2012，29(6):773－777.Chen X Y，Jing Y W，Li C J.Optimal variable tactic control of warfare hybrid dynamic system based on Lanchester equation［J］.Control Theory ＆ Applications，2012，29(6):773－777(in Chinese).

［13］ Chen H M.An optimal control problem in determining the optimal reinforcement schedules for the Lanchester equations［J］.Computers and Operations Research，2003，30(7):1051－1066.

［14］ Draguna V，Frank L.Adaptive dynamic programming for online solution of a zero－sum differential game［J］.Journal of Control Theory and Applications，2011，9(3):353－360.

［15］ 朱寶鎏，朱榮昌，熊笑非.作戰飛機效能評估［M］.2版.北京:航空工業出版社，2006:184－185.Zhu B L，Zhu R C，Xiong X F.Aircraft effectiveness evaluation［M］.2nd ed.Beijing:Aviation Industry Press，2006:184－185(in Chinese).

［16］ 譚東風.基于網絡整體效能的戰斗毀傷模型［J］.系統工程理論與實踐，2013，33(2):521－528.Tan D F.An attrition model with global network efficiency［J］.Systems Engineering－Theory ＆ Practice，2013，33(2):521－528(in Chinese).

［17］ 黃金才，張勇，楊磊，等.戰術數據鏈作戰效能定量評估方法［J］.火力與指揮控制，2010，35(12):66－69.Huang J C，Zhang Y，Yang L，et al.A quantitative evaluation method for operation efficiency of tactical data link［J］.Fire Control ＆ Command Control，2010，35(12):66－69(in Chinese).

［18］ 牛德智，陳長興，班斐，等.基于效能評估的航空作戰進程預測［J］.航空學報，2014，35(5):1416－1423.Niu D Z，Chen C X，Ban F，et al.Prediction on force in air combat process based on effectiveness evaluation［J］.Acta Aeronautica et Astronautica Sinica，2014，35(5):1416－1423(in Chinese).