西溪河特大跨度鋼管混凝土拱橋轉體施工控制

韋有波

(中鐵十八局集團第二工程有限公司，河北唐山063000)

西溪河特大跨度鋼管混凝土拱橋轉體施工控制

韋有波

(中鐵十八局集團第二工程有限公司，河北唐山063000)

采用轉體法施工的鋼管混凝土拱橋，當拱圈在轉動過程中突然停止時，拱圈將承受慣性力、自重和風荷載作用，可能產生較大變形，引起結構局部失穩(wěn)，造成工程事故。以西溪河大橋轉體施工過程中拱腳局部鋼板屈曲為控制目標，通過理論推導和有限元分析，給出了風速、拱圈轉速、扣索拉力和急停時間之間的關系表達式，提出西溪河大橋拱圈轉體施工保守轉速應當控制在0.01 rad/s以內。

拱橋 轉體法 施工控制 屈曲分析

鋼管混凝土拱橋轉體施工法的要旨是將拱圈分為兩個半跨，分別在拱跨兩側利用地形和臨時支架預拼裝半拱，然后通過拱腳轉動裝置及相應動力牽引裝置將兩個半跨拱體逐步轉動至設計拱軸線位置合龍成拱［1］。

目前，關于轉體施工技術的研究不少。范應心［2］對黃柏河、下牢溪兩座鋼管混凝土拱橋轉體施工進行了研究，對轉體施工方案、施工布置、安全技術措施、施工誤差等提出了要求;田仲初等［3］根據一階最優(yōu)化計算理論，構建了采用液壓同步提升技術進行轉體施工拱橋的優(yōu)化有限元模型，將優(yōu)化計算理論應用到拱橋液壓同步提升轉體施工控制中;孫全勝等［4］研究了斜拉橋平轉施工過程中溫度效應的影響，發(fā)現日照方位的變化會引起斜拉橋轉體施工產生不對稱偏移，使轉盤中心處產生不平衡力矩，引起結構發(fā)生傾斜;車曉軍等［5］研究了轉體施工橋梁大噸位球鉸徑向應力，提出了一種優(yōu)化計算方法，并結合工程實測數據進行對比分析，從理論上確保球鉸設計合理可靠;晏敬東等［6］對高墩轉體T構施工控制技術進行了研究，提出了轉體施工過程中的控制標準和方法。

然而在拱圈旋轉施工中，拱圈轉動的速度是最主要的控制因素，它們影響著轉體施工的安全和轉體質量。同時由于在轉體過程中需要將拱圈分為兩個半跨，此時拱圈相當于懸臂梁結構，拱圈的橫向剛度較差，當拱圈在轉動過程中突然停止時，拱圈會承受慣性力、自重和風荷載作用;這些荷載的方向和大小不同，其合力作用方向也會產生變化，當合力作用方向的拱圈抗彎剛度較小時，拱圈可能會產生較大變形或結構鋼板局部失穩(wěn)，對結構產生不利影響。關于鋼管混凝土拱圈穩(wěn)定性研究目前主要有:詹豪等［7］研究了鋼箱梁和混凝土薄壁箱梁受壓翼緣的穩(wěn)定問題，基于狀態(tài)—空間向量法，給出了一種計算方法，該方法可以用于彈性支承連續(xù)矩形薄板彈性屈曲分析;李亮等［8］為了研究核心筒支撐作用對屈曲模態(tài)和屈曲臨界荷載的影響，建立了鋼—混凝土混合結構體系簡化力學模型，并在大量有限元分析的基礎上，研究了鋼—混凝土混合結構體系中框架和支撐兩部分之間的相對強弱關系對屈曲模態(tài)的影響。

有鑒于此，本文結合新建鐵路成都至貴陽線樂山至貴陽段西溪河特大橋，對其轉體施工過程中拱圈的受力進行研究，提出轉體控制速度的限值。

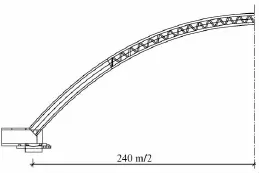
圖1 西溪河大橋立面

1 工程概況

西溪河大橋主橋為上承式X形鋼管混凝土提籃拱橋，跨距為240 m，如圖1所示。拱圈是由2條拱肋和橫向聯結系構成，拱肋橫向內傾7.5°，拱趾處橫橋向中心間距23.192 m，拱頂拱肋中心間距8.71 m，主拱在其傾斜平面內拱軸線為懸鏈線，拱軸系數m=2.2，矢跨比約1/4.364。拱肋高5.7 m，寬3.0 m，每肋由4肢φ 1 100 mm×20 mm鋼管構成，其上下弦是由2肢鋼管與2塊20 mm厚的鋼板聯結成啞鈴形，并且沿拱肋全長采用等截面(圖2);從拱趾處向拱肋兩端各約53.0 m范圍內的上下弦之間是由2塊16 mm厚的鋼板聯結，使拱肋斷面形成箱形結構。拱肋的中部其上、下弦之間通過H形腹桿(H600 mm×500 mm× 20 mm×20 mm)連接形成拱式桁架。

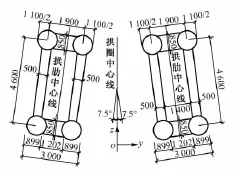
圖2 拱腳處橫斷面(單位:mm)

2條拱肋之間其上、下弦采用φ800 mm×20 mm (平聯直管)以及φ600 mm×16 mm(平聯斜管)鋼管組成的多道Ж字形的平聯聯結;上、下弦平聯之間采用φ450 mm×16 mm(豎管)鋼管斜向聯結，以此組成拱肋橫向聯結系。

2 板的屈曲理論分析［9］

拱圈在轉體過程突然停止時，在慣性力和風荷載作用下，靠近拱腳處會產生較大的平面外彎矩，使拱肋上兩肢鋼管間的腹板處于受壓狀態(tài)，如圖3所示［9］。當壓應力σx逐漸增加到一定數值即翹曲臨界應力時，平板就會開始翹曲。板的翹曲撓度用ω表示。

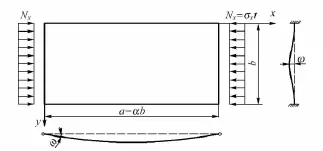
圖3 矩形薄板的撓曲

板翹曲以后，板中面的撓曲方程式可以表達為

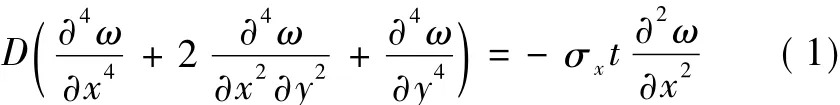
式中:D為板的單位寬度的抗彎剛度，D=Et3/［12× (1-v3)］;v為泊松比;t為板的厚度。

方程式(1)的解可以寫成雙重三角級數

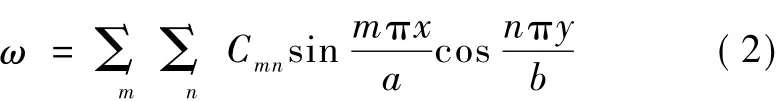
式中:m=1，2，3，…，n=1，2，3，…，分別表示在x和y方向板撓曲的半波數目;Cmn為待定常數。

式(2)能夠滿足固定板的邊界條件，即在x=0，x=a和y=0，y=b處，板支點上的撓度和轉角滿足邊界條件。將式(2)代入式(1)中，可以得到以下方程

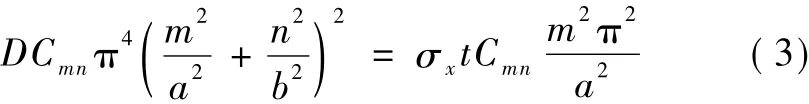
由此可得板的撓曲臨界應力

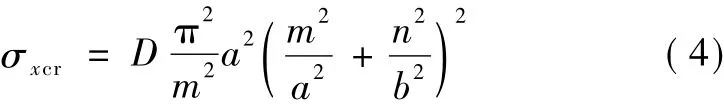
為了得到最小的臨界應力，顯然應有n=1，這就是說，在y方向板撓曲成一個半波。至于m的具體值，則須視板長比α=a/b而定。

將上式進一步簡化，則有

式中，k為板的撓曲系數，k=(m/α+α/m)2。

相關研究可知，對于兩邊(y向)固結的板，其翹曲系數k=6.97，y向撓曲半波長l0=0.67b。則此時板的撓曲臨界應力為

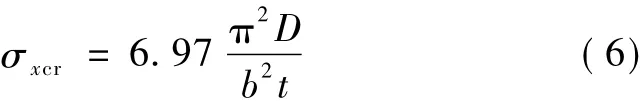
3 風速與拱肋轉速關系方程

由力學知識可知，應力和外力的關系為

1)軸力N的計算

單支拱肋受力示意如圖4。

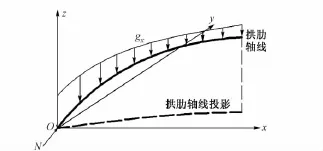
圖4 單支拱肋受力示意

對半拱單支拱肋進行受力分析，在計算單支拱肋軸力時，忽略拱肋之間的橫向聯系引起的拱肋軸力。可以知道單支拱肋軸力

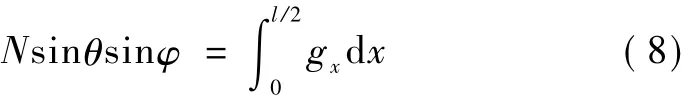
因此

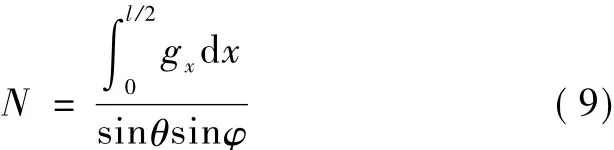
式中:θ為拱肋軸線平面內拱腳與水平方向夾角;φ為拱肋軸線與豎直平面的傾角;gx為拱肋自重集度。詳見圖5、圖6。

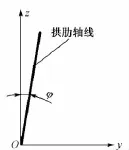
圖5 單支拱肋側視

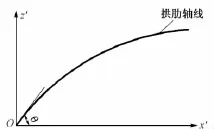
圖6 拱肋軸線立面

2)彎矩M的計算

由于拱圈在旋轉施工過程中突然停止時，拱圈所受荷載為風荷載、自重和慣性力荷載。在荷載作用下，拱腳根部會產生兩個方向的彎矩My和Mz

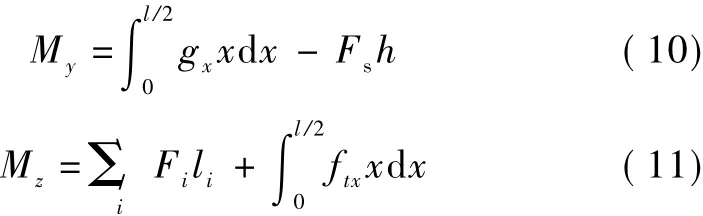
式中:Fi為拱圈第i部分構件所承受的風荷載;li為拱圈第i部分的長度;l為拱圈跨徑;ftx為拱圈轉體施工過程中拱圈慣性力集度;Fs為拉索拉力;h為拱肋拉索錨固點到拱腳處豎向距離。

根據《公路橋涵設計通用規(guī)范》［10］規(guī)定可以知道，拱圈所受風荷載可以采用下式計算。

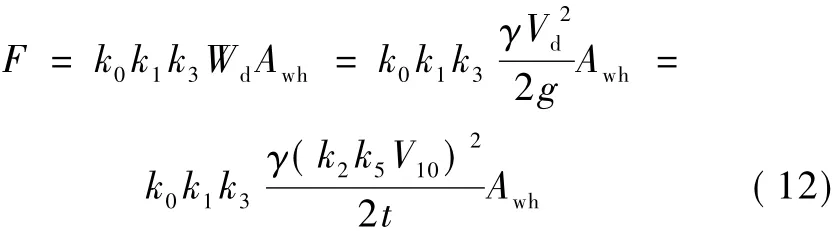
式中:k0為設計風速重現期換算系數;k1為風載阻力系數;k2為考慮地面粗糙度類別和梯度風的風速高度變化修正系數;k3為地形地理條件系數;k5為陣風風速系數;g為重力加速度;Wd為設計基準風壓;Awh為橫向迎風面積;V10為橋梁所在地區(qū)的設計基本風速;Vd為高度Z處的設計基本風速，Z為距離地面或水面的高度;γ為空氣重力密度，γ=0.012 017e-0.0001Z。

根據沖量定理，可以得到拱圈慣性力集度ftx。

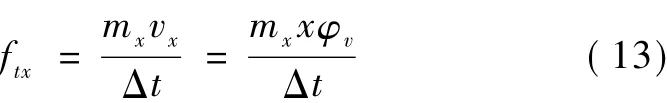
式中:mx為拱肋單位長度上的質量;vx為拱肋轉動線速度;φv為拱肋轉動角速度;Δt為拱肋突然停止轉動所用時間。

將式(12)和式(13)代入式(11)，可得

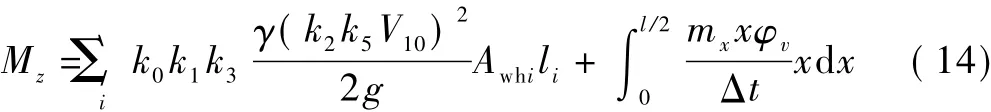
將式(9)、式(12)和式(14)代入式(7)，可得

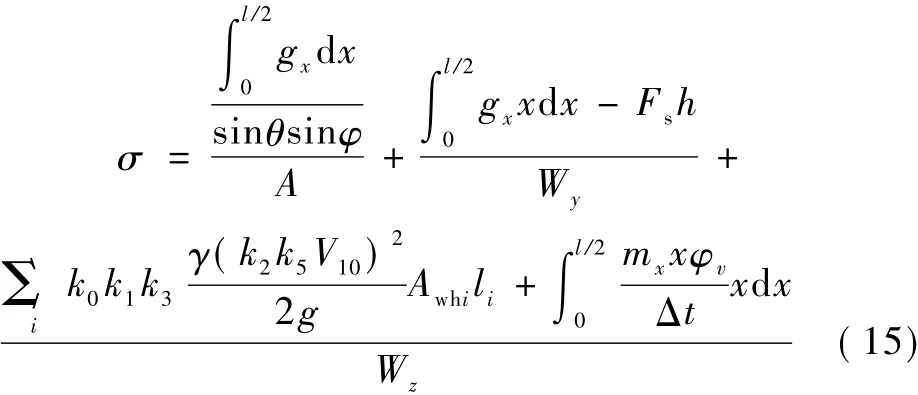
當拱腳拱肋腹板屈曲時，σ=σcr，可得拱肋腹板屈曲時風速與拱肋轉速關系

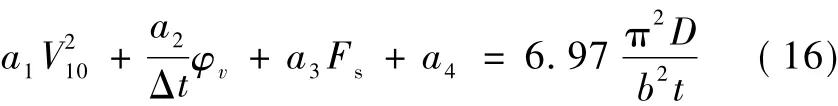
其中

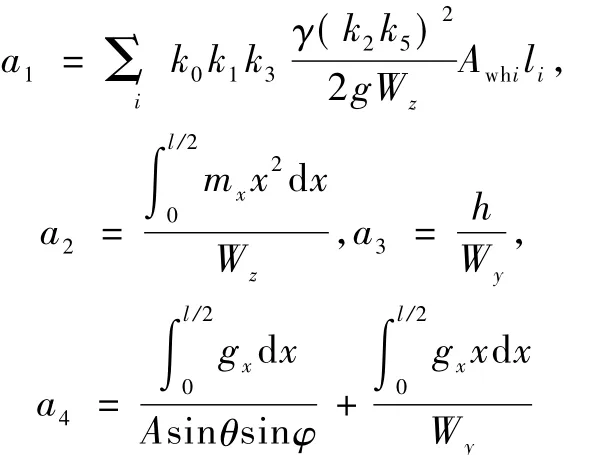
4 有限元模型及分析

利用有限元軟件建立西溪河大橋半跨拱肋結構三維模型。拱肋鋼管和拱肋腹桿用梁單元模擬，拱肋上的鋼板采用板單元模擬，水平扣索用桁架單元模擬，拱肋拱腳處采用固定約束，扣索錨固端設置豎向約束、橫向約束和水平約束。總共采用3 200個梁單元，4 488個板單元和1個桁架單元。結構有限元模型如圖7所示。

利用建立的有限元模型計算出公式(16)中各個系數的值。

1)各荷載加載值計算

①風荷載

風荷載按照風速為1 m/s進行計算，根據西溪河大橋拱肋各構件參數計算，可得各構件所施加風荷載，見表1。

圖7 半跨拱圈模型

表1 拱肋各構件風荷載

②慣性力

慣性力荷載按照轉速1 rad/s進行計算，由于各點的質量集度和矩轉軸的距離不同，因此依據慣性力合力和作用點相同的原則，各點慣性力可以近似為

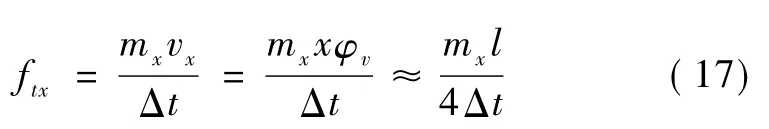
③扣索索力

為了方便計算系數a3，扣索索力按1 000 kN施加。

2)系數計算結果

通過分析可以知道拱肋拱腳處壓應力最大，此時可以得出各系數為a1=0.001，a2=400.6，a3= -0.000 1，a4=8.1。將各系數代入式(16)可以得到

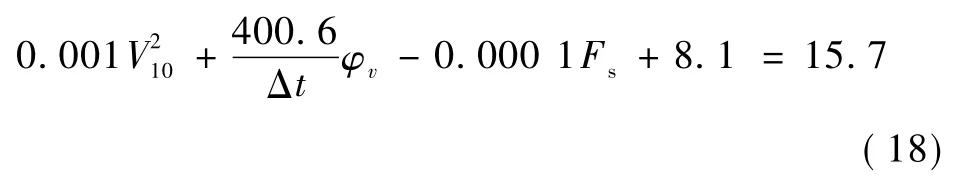
由于0.000 1Fs較其他幾項小很多，因此上式可以寫為

3)風速與拱圈轉速的關系

根據公式(19)可以做出當Δt在0.1～1 s變化時的風速與拱圈轉速的關系曲線，如圖8所示。

對圖8進行分析可以知道:

①當拱肋突然停止轉動所用時間保持不變時，隨著風速的增加，拱圈轉速呈拋物線減小。

②當風速保持不變時，隨著轉速的增加，拱肋突然停止轉動所用時間逐漸增大。

③當轉速保持不變時，隨著風速的增加，拱肋突然停止轉動所用時間逐漸增大。

④拱圈轉體施工的保守轉速為0.01 rad/s。

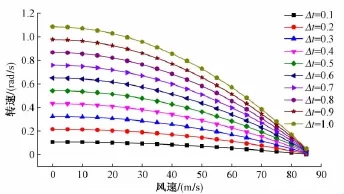
圖8 風速與拱圈轉速的關系曲線

5 結論

通過對西溪河特大跨度鋼管混凝土拱橋轉體施工過程進行理論研究和有限元分析，得到以下結論:

1)在西溪河特大跨度鋼管混凝土拱橋轉體施工過程中，以拱肋腹板屈曲為控制目標，通過理論分析給出了風速與拱圈轉速關系函數表達式。

2)給出了西溪河特大跨度鋼管混凝土拱橋轉體施工的保守轉速為0.01 rad/s。

3)為了確保西溪河特大跨度鋼管混凝土拱橋轉體施工安全快速的完成，在施工過程中應該實時監(jiān)測風速，并且結合實測風速對拱圈轉速進行調整。

［1］張聯燕，程懋方，譚邦明，等.橋梁轉體施工［M］.北京:人民交通出版社，2003.

［2］范應心.160 m鋼管混凝土拱的轉體施工［J］.橋梁建設，1996(3):4-6，11.

［3］田仲初，劉雪鋒，顏東煌，等.優(yōu)化計算在拱橋液壓同步提升轉體施工控制中的應用［J］.中國公路學報，2008，21 (2):74-78.

［4］孫全勝，傅科奇.綏芬河斜拉橋轉體施工溫度影響分析［J］.公路交通科技，2006，23(10):55-59.

［5］車曉軍，周慶華，關林坤.轉體施工橋梁大噸位球鉸徑向應力計算方法優(yōu)化研究［J］.武漢理工大學學報(交通科學與工程版)，2014，38(2):356-358.

［6］晏敬東，陳強.150MN高墩轉體T構施工控制技術［J］.橋梁建設，2012，42(1):102-107.

［7］詹豪，邵旭東，蔣志剛.多跨彈性支承連續(xù)矩形薄板屈曲分析［J］.工程力學，2014，31(11):25-30，38.

［8］李亮，李國強.鋼—混凝土混合結構體系屈曲模態(tài)判別標準及臨界荷載簡化算法［J］.建筑科學與工程學報，2014，31(4):67-73.

［9］李國豪.橋梁結構穩(wěn)定與振動［M］.北京:中國鐵道出版社，2010.

［10］中華人民共和國交通部.JTG D60—2004公路橋涵設計通用規(guī)范［S］.北京:人民交通出版社，2004.

(責任審編孟慶伶)

U445.465;TU311.2

A

10.3969/j.issn.1003-1995.2015.12.04

1003-1995(2015)12-0015-04

2015-08-18;

2015-11-06

韋有波(1981—)，男，工程師。