蒙山天池堆石自密實混凝土拱壩三維有限元分析

郁章文 劉 剛

(山東省臨沂市水利勘測設計院，山東臨沂 276000)

1 引言

蒙山天池堆石自密實混凝土拱壩壩體采用單曲拱壩，最大壩高24.0m，壩頂外弧半徑為50m，最大中心角為78°。壩長130m，其中中間拱壩段68m，左端重力墩28.46m(包括拱座)，右端重力墩33.54m(包括拱座)，分別與兩岸連接。壩頂高程815.00m，拱壩壩頂寬度為4.0m，最大壩底寬為10.0m。壩體斷面上游面為鉛直面，下游面為折坡，上部3m為直線段，下部坡比為1∶0.33。壩頂設4孔溢流堰，總凈寬20m，堰頂高程814.00m。詳見圖1、圖2。

蒙山天池工程筑壩材料采用堆石自密實混凝土。堆石混凝土是在自密實混凝土技術基礎上發展起來的一種新型大體積混凝土施工技術，已獲得國家專利。堆石混凝土施工首先將滿足一定粒徑要求的堆石直接入倉，形成有空隙的堆石體，然后在堆石體表面澆筑滿足特定要求的自密實混凝土，利用其特有的高流動、抗離析、強填充黏結性能，依靠自重完全充填堆石體空隙，形成完整、密實、有較高強度和低水化熱的大體積混凝土。自密實混凝土是指在澆筑過程中無需施加任何振搗，僅依靠混凝土自重就能完全填充至模板內任何角落和鋼筋間隙的混凝土。

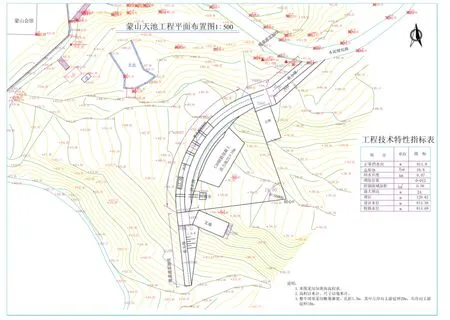
圖1 蒙山天池平面布置

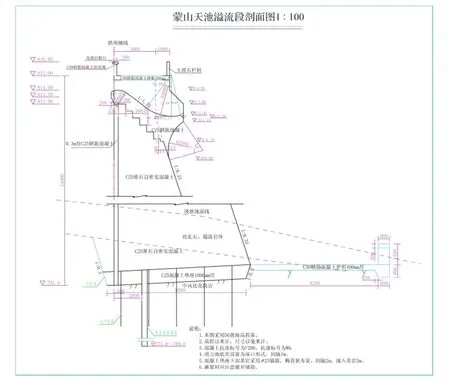
圖2 蒙山天池溢流段剖面

根據蒙山天池拱壩的工程特點，利用大型軟件ANSYS，建立拱壩的三維非線性有限元分析模型，仿真模擬拱壩的運行性態，研究拱壩在運行期的應力變形特性，分析評價拱壩結構設計的合理性和安全性，并相應優化調整拱壩設計，滿足工程需求。

2 計算理論

ANSYS程序提供一種以Drucker-Prager為屈服準則的材料，該材料選項適用于混凝土、巖石土壤等顆粒狀材料。

Drucker-Prager準則實際是對Mohr-Coulomb準則的修正。由于Mohr-Coulomb準則在π平面上的屈服軌跡為六角形，它在主應力空間的屈服面有一個奇異的頂點，為消除角點，Drucker和Prager對其提出修正，他們建議用一個正圓錐面來代替上述的不規則六角錐面。在π平面上的屈服軌跡為一圓。其屈服函數表示為

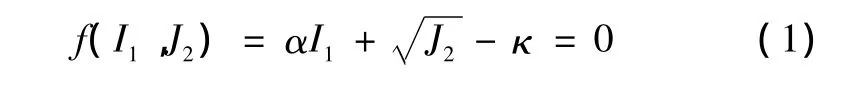
式中 I1、J2——分別為應力張量的第一不變量和應力偏張量的第二不變量;

α、κ——為材料常數，它們與內摩擦角 φ和黏聚力c的關系為

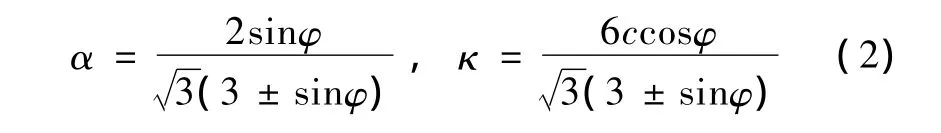
其中，“+”號對應于 Drucker-Prager圓錐面與Mohr錐體的內角點相接，“-”號則對應于 Drucker-Prager圓錐面與Mohr錐體外接。若取α=0，則其退化為Mises準則－κ=0。

反映材料本構關系的彈塑性矩陣Dep為Dep=D(1－r)DP(3)

式中 D、Dp——分別為彈性與塑性本構陣;

A——為材料硬化參數。

由于ANSYS采用的Drucker-Prager屈服面為Mohr-Coulomb屈服面的外接圓錐，式(2)取“-”。屈服面不隨材料的逐漸屈服而改變，即沒有強化準則，但屈服強度隨側限壓力的增加而相應增加，塑性行為假定為理想彈塑性。采用相關聯流動法則，即流動方程是塑性應變在垂直于屈服面的方向發展的屈服準則中推導出來的。考慮由于屈服而引起的體積膨脹，但不考慮溫度變化的影響。另外，塑性應變的大小與加載速度無關。

對DP材料，其受壓時的屈服強度大于受拉時的屈服強度。如果有材料的單軸受拉屈服應力和單軸受壓屈服應力，可以通過下式將此二值轉換為程序所需的輸入值

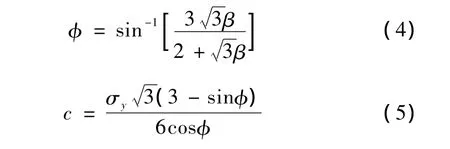
式中 β和σy可由受壓屈服應力和受拉屈服應力計算出

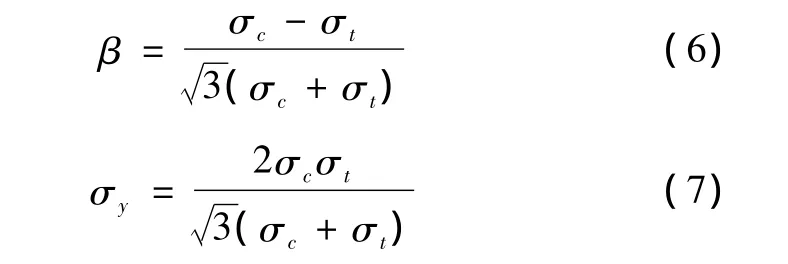
3 計算模型

3.1 網格生成

根據有限元設計規范及參考相關類似工程，利用有限單元法計算拱壩應力時，單元的剖分應盡量達到設計所要求的精度，單元形式結合拱壩體型合理選用。計算坐標系規定為:X軸為壩軸線向(橫河向)，由左岸指向右岸;Y軸為順河向，指向下游;Z軸為垂直向，豎直向上，與高程一致。

根據蒙山天池拱壩的壩體結構及壩基巖體的資料(包括斷面、地質剖面等)，結合類似工程經驗，截取有限元模型計算范圍如下:橫河向截取長度總計為200m，左岸截取至左岸壩肩以外44.0m，右岸截取至右岸壩肩以外42.0m;順河向截取長度總計為100m，上游截取至壩踵以外31.5m，下游截取至壩趾以外58.5m;鉛直向上邊界按地形實際高度模擬，底部邊界截取至壩基面以下41m;三個方向截取范圍均為1～2倍壩高。此外，該三維有限元整體模型忽略了放水洞等附屬結構的影響。

有限元模型劃分網格時，遵循盡量模擬壩體的實際形態的原則，使之反映壩體的實際情況。模型離散后，單元結點總數為14479個，單元總數為12135個，蒙山天池拱壩三維有限元網格如圖3所示。拱壩壩體沿高度方向自動剖分為12層，沿厚度方向剖分為4層，拱壩壩體有限元網格如圖4所示。

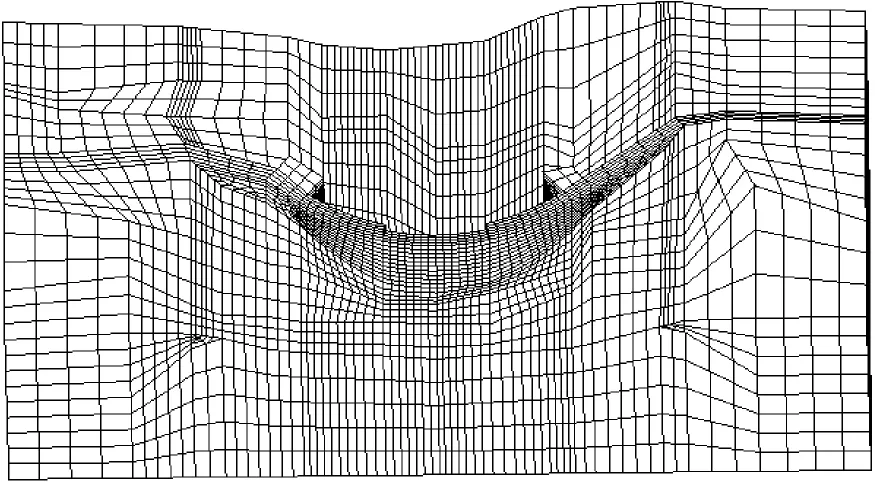
圖3 蒙山天池拱壩三維有限元網格

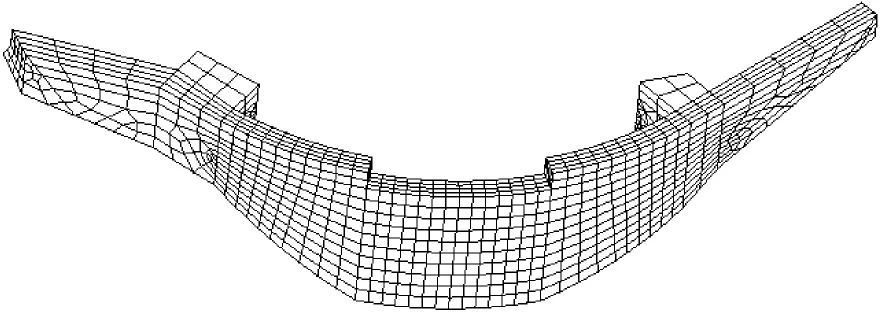
圖4 蒙山天池拱壩壩體有限元網格

3.2 計算參數

溫度應力分析時，利用ANSYS熱分析模塊，采用solid70單元模擬拱壩壩體和壩基巖體;應力場分析時，利用ANSYS靜力分析模塊，采用solid45單元模擬壩基巖體，采用solid65單元模擬混凝土單元。

根據蒙山天池拱壩壩體設計資料以及壩基巖體勘測資料，拱壩及重力墩等壩體材料采用堆石混凝土，壩基材料主要為中風化花崗巖，各材料的具體計算參數如表1所列。

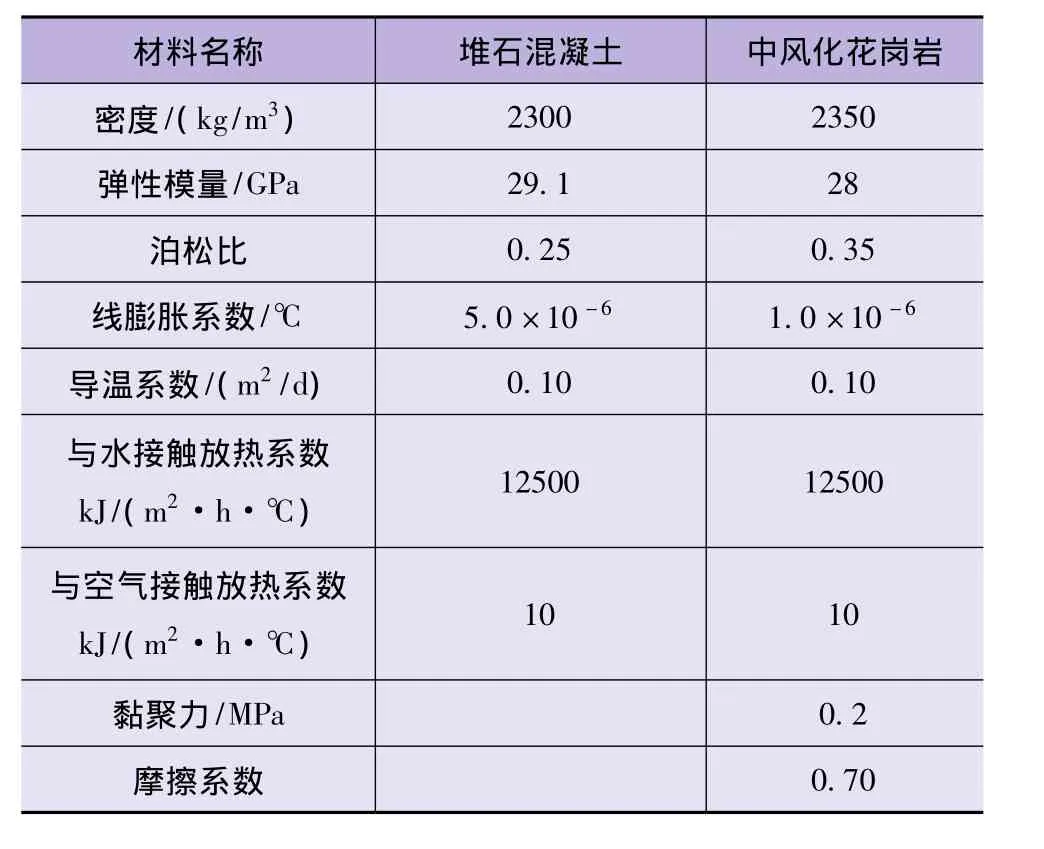
表1 材料參數

3.3 計算工況

根據《混凝土拱壩設計規范》(SL 282—2003)中的相關規定，本次分析考慮了自重、上下游靜水壓力、溫度荷載和揚壓力等不同組合。壩體自重不考慮分期施工的影響。

混凝土拱壩設計荷載組合分為基本荷載組合和特殊荷載組合兩類。基本組合由基本荷載組成，特殊組合除相應的基本荷載外，還應包括某些特殊荷載。

3.3.1 基本組合

工況1:正常蓄水位+正常溫降+自重+揚壓力;

工況2:設計洪水位+正常溫升+自重+揚壓力;

工況3:死水位+正常溫降+自重+揚壓力;

工況4:死水位+正常溫升+自重+揚壓力。

3.3.2 特殊組合

工況5:校核洪水位+正常溫升+自重+揚壓力。

3.4 計算成果

根據已建立的三維有限元分析模型、計算參數和荷載組合工況，利用有限元分析軟件ANSYS，分別計算蒙山天池拱壩基本組合工況和特殊組合工況下的位移和應力分布。

基本組合工況和特殊組合工況下的各工況計算得到的特征位移如表2所示，特征應力見表3。

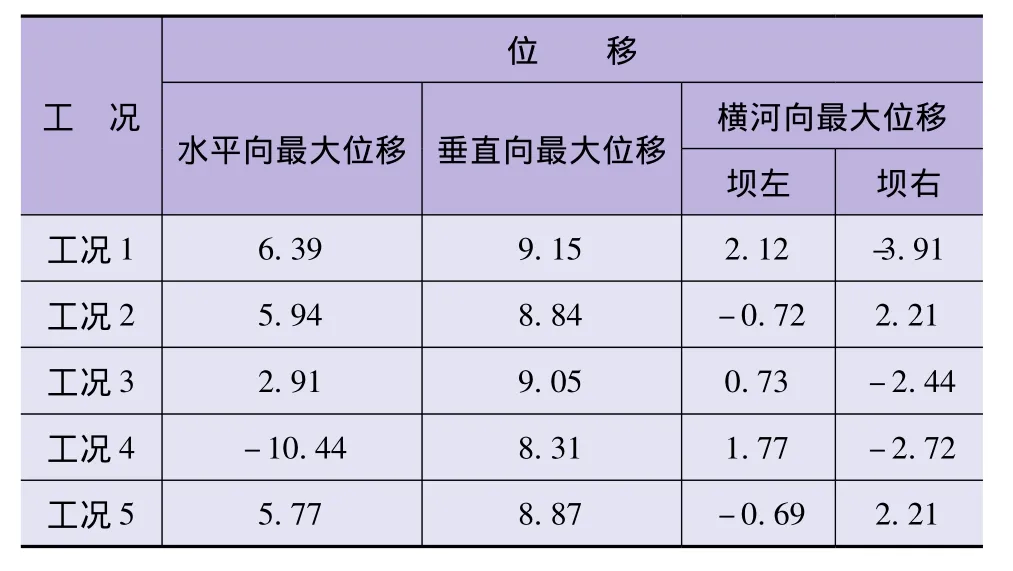
表2 各工況中壩體最大位移統計 單位:mm

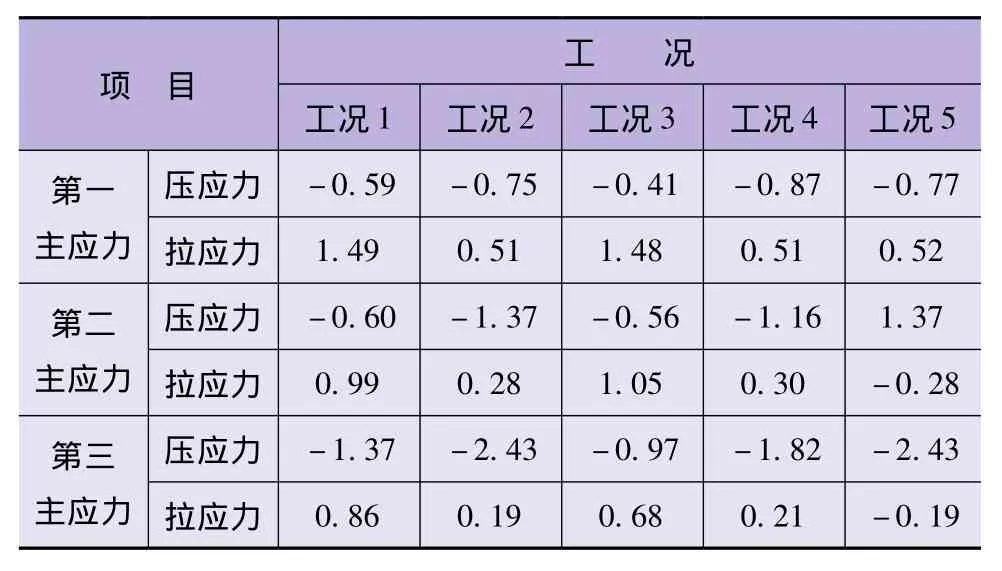
表3 各工況中壩體最大應力統計

3.5 成果分析

3.5.1 位移分析

從各計算工況的位移可知，壩體的順河向、橫河向、豎直向三個方向的位移均表現出關于拱冠梁斷面的對稱性。從表2可知:工況1、工況2和工況3壩體向下游向發生徑向位移，最大位移發生在壩頂溢流壩段處;工況1(正常水位+溫降)和工況3(死水位+溫降)由于上游水壓力和溫降荷載的共同作用，順河向位移分別為6.39mm和2.91mm;工況2(設計洪水位+溫升)和工況5(校核洪水位+溫升)，壩體受高水位靜水壓力的影響，其水平位移基本偏向下游但由于受溫升溫度場的影響，偏向下游量有所減少，最大值為5.94mm和5.77mm，處于拱冠梁頂部、拱端和拱座的局部附近區域，由于受溫升溫度荷載的影響，壩體水平位移偏向上游，最大值分別為0.36mm和0.37mm，處于壩體拱端。在工況4(死水位+溫升)下，由于水壓力荷載較小，受溫升作用影響明顯，壩體向上游向徑向位移較大，其值達10.44mm，主要是由于拱壩溫升荷載較大，而且壩體單薄受溫度荷載影響明顯。

在各工況下，通過綜合比較壩體與壩基的位移，壩體的各位移變化量要比壩基位移大，其中壩體沉降量最大值為9.15mm，均小于最大壩高的1%，壩體水平位移和沿壩軸線向位移均在mm數量級左右，因此該壩體位移符合拱壩位移的一般規律。

3.5.2 應力分析

本次計算中只考慮溫度場變化對應力場的影響，忽略壩體應力變化對溫度場的影響。從各計算工況的位移可知，拱壩壩體應力也表現出關于拱冠梁斷面的對稱性。通過對各荷載組合情況下大壩三維有限元的應力計算，可知壩體上游面的壓應力一般來說都是隨著水位的升高而增大，上游面的拉應力也隨著水位的升高而增大。通過對各荷載組合情況下大壩三維有限元的應力計算，可知壩體上游面的壓應力一般來說都是隨著水位的升高而增大，上游面的拉應力也隨著水位的升高而增大。壩體第三主應力基本為壓應力，僅有局部區域出現拉應力，根據溫度場的變化，拉應力位置也有所不同，但其分布范圍較小。

在各工況下，通過綜合比較壩體應力分布圖和表3，壩體在工況2(設計洪水位+溫升)和工況5(校核洪水位 +溫升)的最大壓應力值分別為2.43MPa和2.43MPa，小于混凝土抗壓強度4.5MPa。工況1(正常蓄水位+溫降)和工況3(死水位+溫降)下，壩體局部拉應力區較大，最大值分別為1.49MPa和1.48MPa，其值小于抗拉要求值1.5MPa，并且在壩體拉應力較大部位鋪設鋼筋后，壩體抗拉強度進一步提高，同時由于壩基面應力計算時存在應力集中問題，實際應力應小于計算值，因此，從應力角度來看，壩體可滿足抗拉強度和抗壓強度要求。

4 結語

根據蒙山天池拱壩的實際情況，結合三維非線性靜力有限元計算分析結果可以得到以下結論:

a.通過三維非線性有限元計算，得到壩體的應力場和位移場分布符合一般變形規律，驗證了壩體應力和位移分布的合理性。

b.通過三維非線性有限元計算，得到了壩體在各工況下的最大壓應力值為2.43MPa，最大拉應力值為1.49MPa，均可滿足規范強度要求。

c.通過計算分析可知，溫降作用下，溫度荷載使得壩體壩軸線縮短，整體變形指向上游，使得壩體的拉應力增加，對壩體的應力有一定的不利影響;溫升作用下，溫度荷載引起壩體向上游位移，在拱端產生較大的壓應力，對穩定有一定的不利影響，但壩體變形及應力均在規范允許范圍內。

d.拱壩壩體與重力墩連接處存在較大的拉應力和壓應力，主要是由于應力集中所引起的，實際應力應小于計算值，且壩體內鋪設鋼筋后，壩體抗拉強度進一步提高。因此，從應力角度來看，壩體可滿足抗拉強度和抗壓強度要求。■

［1］ 肖偉榮，蘇志敏，唐濤.有限元等效應力法在拱壩設計中的應用［J］.云南水力發電，2005(1):36-39.

［2］ 武亮，葉文明，何仕華.基于ANSYS的拱壩等效應力分析［J］. 水利水電技術，2006，48(9):27-29.

［3］ 黎滿林，任青文，陸曉敏.兩河口拱壩的三維非線性有限元分析［J］. 水電站設計，2008，24(4):26-29.

［4］ 任青文，余天堂，趙引.錦屏高拱壩整體安全度研究和評價［R］.南京:河海大學土木工程學院，2005.