基于改進Floyd算法的裝配供應鏈網絡路徑選擇研究

江玉杰

（三江學院商學院，江蘇 南京 210012）

基于改進Floyd算法的裝配供應鏈網絡路徑選擇研究

江玉杰

（三江學院商學院，江蘇 南京 210012）

運用Floyd算法從鏈上整體效益角度研究裝配供應鏈網絡路徑選擇問題，并綜合考慮響應速度、服務質量、物流成本對網絡路徑選擇的影響，引進綜合修正因子，以改進傳統Floyd算法。結合實例分析結果表明，運用改進Floyd算法選擇裝配供應鏈最優網絡路徑更加貼近現實、更加節省，從而增進鏈上各節點企業之間的合作程度，最終實現裝配供應鏈穩健高效的運行。

Floyd算法；裝配供應鏈；網絡路徑選擇

0 前言

裝配供應鏈是指以裝配制造商為核心，集聚零部件供應商、集配商、分銷商、零售商以及配送中心等相關輔助企業，為滿足顧客不同需求而形成的供需網絡。而裝配供應鏈各節點企業，由于空間距離的限制、各企業的經營特點，需借助運輸、配送等物流方式將所需調運的物資按時送達指定的地點，此時所消耗的費用高低、響應速度的快慢、物流質量的優劣必然會影響裝配供應鏈穩定、高效的運行。因此，合理、有效的裝配供應鏈網絡路徑，能夠降低鏈上各節點企業之間的距離、降低物流成本、提高物流質量，進而提高供應鏈的柔性，最終實現鏈上的整體收益大于各自單獨運營時所獲收益的總和[1]。

目前，專門研究裝配供應鏈網絡路徑的文獻相對較少，文獻《基于時間Petri網的供應鏈網絡關鍵路徑分析》[2]采用時間 Petri網研究供應商、生產商、分配中心、零售商、顧客5級供應鏈網絡關鍵路徑；文獻《基于VRP模型的兩階段物流網絡路徑優化模型》[3]基于VRP模型研究供應商、物流中心2級供應鏈物流網絡最優化路徑；文獻《動態閉環復雜配送網絡路徑優化算法研究》[4]將正向配送與逆向配送相結合，運用動態規劃算法研究閉環配送網絡最優化路徑；文獻《基于復雜網絡理論的物流配送路徑優化研究》[5]以復雜網絡理論為基礎，利用動態規劃算法研究物流配送最優化路徑；文獻《供應鏈彈性綜合優化路徑選擇模型分析》[6]根據木桶理論與效價理論找出供應鏈中的彈性瓶頸，構造供應鏈彈性綜合優化路徑；文獻《基于Floyd算法的供應鏈網絡路徑研究》[7]以拉動式生產為前提條件，運用Floyd算法研究制造商、配送中心、銷售商3級供應鏈網絡路徑優化。

上述文獻采用不同的理論（時間Petri網、VRP模型、動態規劃算法等）對供應鏈中部分節點企業之間路徑進行優化，各有優勢，但總體上僅局限于以最低物流成本為指標選擇供應鏈網絡路徑。鑒于此，本文將以改進Floyd算法研究針對包含響應速度、服務質量、物流成本3項指標的，由供應商、集配商、制造商所組成的裝配供應鏈網絡路徑選擇問題。

1 問題描述

1.1 研究對象

裝配供應鏈中的核心企業即裝配制造商，依據TOC理論中關于生產企業分類原則屬于A型企業。而A型企業最大的特點是生產過程所需原材料種類很多，甚至有些零部件是最終產品的專用件（即屬于卡拉杰克模型中的戰略項目）。因而，裝配供應鏈最大的特點是裝配制造商的某項需求將驅動上游多家供應商提前通過集配商的運輸、配送等物流方式，將所需調運的物資及時、有效的送到指定的地點。基于此，本文研究3個供應商、2個集配商、1個制造商所組成的裝配供應鏈網絡路徑選擇問題。所研究的裝配供應鏈網絡路徑如圖1所示。

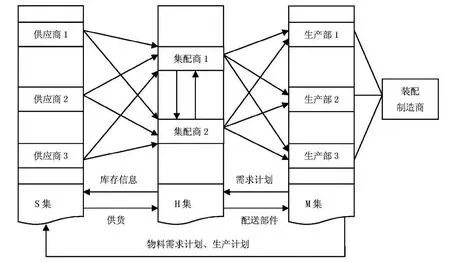
圖1 裝配供應鏈網絡路徑

當5者建立虛擬的動態聯盟時，裝配制造商（M集）首先根據銷售商反饋的銷售信息，制定各區域生產計劃，利用多級滾動計劃向S集（各供應商）、H集（各集配商）發布物料需求計劃；其次，各供應商根據制造商發布的生產計劃、各集配商反饋的庫存信息以及自身生產系統能力大小合理的組織零部件生產；再者，各集配商則會根據各供應商的供貨批量大小合理的組織貨物的運輸，并對其進行集中管理，同時依據制造商的物料需求計劃將零部件配送至各生產部；當遇到特殊情況時，并征求供應商、制造商都同意的前提下，集配商之間可以相互調撥物資以滿足裝配制造商的需求[1]。在此運作模式下，裝配供應鏈便形成復雜交錯的網絡路徑。

1.2 假設前提

在現實社會中，裝配供應鏈各節點企業通常處于多條供應鏈中，為了便于研究裝配供應鏈網絡路徑選擇問題，本文做出如下假設：

1）裝配供應鏈各節點企業能實現信息完全共享且鏈條運作正常。

2）S集中的各供應商的供貨能力相同且無明顯限制，并通過H集中的集配商統一供貨給制造商各區域生產部。

3)在緊急情況下（如供應商突發停產、自然災害以及其他不可抗力情況等），并獲得其他供應商以及制造商同意的情況下，集配商之間可以相互調撥物資。

4）裝配供應鏈最優網絡路徑選擇以綜合指標值最小為衡量標準。

2 建立數學模型

2.1 基于傳統Floyd算法的網絡路徑選擇

Floyd算法，又稱弗洛伊登算法、插點法，是一種用于尋找給定的加權網絡圖中任意2個頂點之間最短路徑的算法，邊權可正可負[8]。

2.1.1 符號描述

本文所研究的裝配供應鏈中涉及8個節點，根據Floyd算法原理可設：

1）供應商1~3分別為v1、v2、v3，集配商1~2分別為v4、v5，裝配制造商中的生產部1~3分別為v6、v7、v8，則裝配供應鏈網絡路徑中頂點的集合可表示為：V=｛v1,v2,v3,v4,v5,v6,v7,v8｝；

2）（vi,vj）表示一條從頂點vi（i=1,2,…,8）指向vj（j=1,2,…,8）的弧，則裝配供應鏈網絡路徑中弧的集合可表示為：A=｛（vi,vj）｝。

3）裝配供應鏈網絡路徑的權矩陣：D=（dij）8x8。

其中，d=lij表示：頂點vi到vj有直接相通的弧時，通過此路時所花費的費用；dij=∞表示；頂點頂點vi到vj沒有直接相通的弧時，無法通過此路，即想要通過此路時將花費無窮大的費用。進而簡化的裝配供應鏈網絡路徑如圖2所示。

2.1.2 算法步驟[8]

1）根據裝配供應鏈網絡各弧路權值（即通過此路所花費的費用），可寫出初始權矩陣D（0）=D。

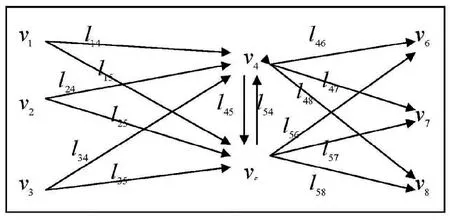
圖2 簡化的裝配供應鏈網絡路徑

2）依次計算D（k）=（）8×8，其中d=min（k=1,2,…,8）。而（dij）（k）表示從頂點vi到vj取其直接有弧或借v1、v2、…vk、點為中間點時的最小費用中的最小值[8]。

3）迭代到第8次即可得到裝配供應鏈網絡路徑的最優解，此時任意兩點間的最小費用為：D（8）=（）8×8。值得注意的是在每次迭代時可保留下標信息，既可給出每次迭代后任意兩點間的最小費用，也可給出具體路徑的最低費用。

2.2 基于改進Floyd算法的網絡路徑優化

運用傳統 Floyd算法選擇網絡路徑只是基于最低物流成本指標，并沒有考慮因路徑的長短導致裝配供應鏈的響應速度、物流質量的差異。在現實社會中，任意兩點間的路長與通過此路所花費的費用并不成正比。倘若僅以最低物流成本為指標選擇網絡路徑，可能因路長相對過遠而使供應商供貨提前期拉長、集配商物流服務質量下降、制造商因缺短貨而停工待產，致使影響裝配供應鏈的穩定性[6]。

為此，本文綜合考慮裝配供應鏈的響應速度、物流質量的影響，引入通過vi到vj路物流費用的綜合修正因子ij，并以lij+ij作為新的路權值。然后重新運用傳統的Floyd算法求解，即通過8次迭代后便可求出裝配供應鏈網絡路徑的最優解。值得注意的是通過路徑仿真技術、先驗數據挖掘技術等，可以在既定的置信區間內估計求得綜合修正因子ij值。

3 實例分析

C.M汽車裝配集團成立于1980年6月，座落在風景秀麗的深圳。受到今年4、5月份汽車供銷量的下滑，加之原先部分零部件供應商終止供貨，公司高層需要重新規劃零部件進貨渠道。經過幾月磋商，已建立新的裝配供應鏈網絡路徑。目前，該公司的生產部1、2、3需進一批零部件，可選進貨路線如圖3所示。其中，各節點之間的物流費用為每條弧上的權值，單位為萬元；v1、v2、v3分別表示供應商A、B、C；v4、v5分別表示集配商1、2；v6、v7、v8分別表示C.M汽車裝配集團的生產部1、2、3。

3.1 背景資料

1）供應商A、B、C向C.M汽車裝配集團的生產部1、2、3供應相同的零部件，即克萊斯勒發動機、采埃孚自動變速箱、普萊德電池，且產品性價比相當。

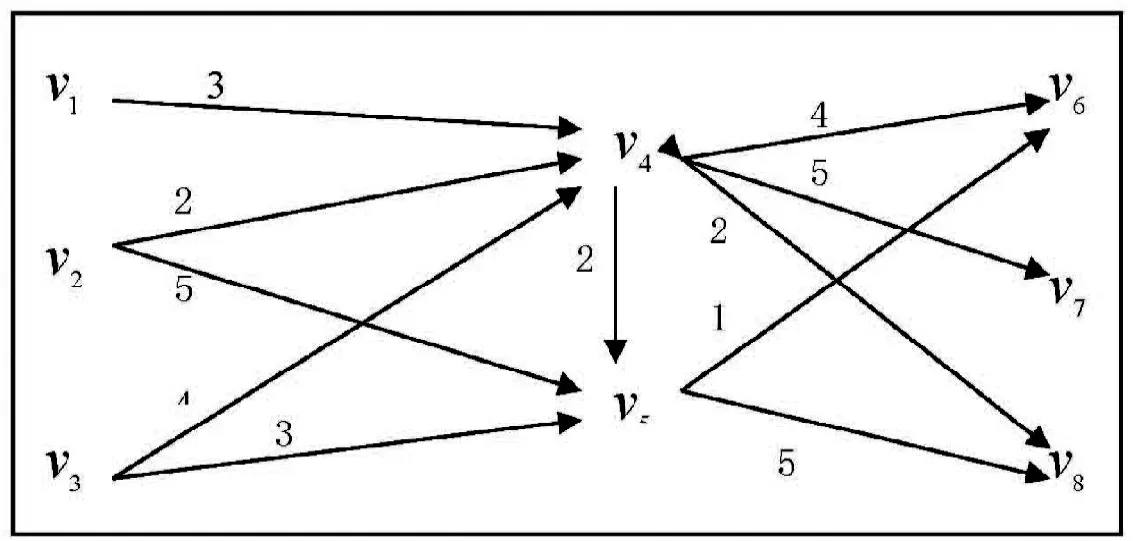
圖3 裝配供應鏈賦權網絡路徑

2）根據公司高層之間的磋商，集配商2可向集配商1調貨，但集配商1不可以向集配商2調貨，并約定供應商向 C.M汽車裝配集團生產部供貨需事先將零部件提前轉運到集配商1、2處進行統一管理，以便實現共同配送。

3）由于供應商A所處地理位置因素，只能將零部件轉運到集配商1處。4）因生產部2的生產規模相對較小，只需由集配商1負責配送零部件。

3.2 運用傳統Floyd算法的網絡路徑選擇

1）基于傳統Floyd算法步驟，結合圖3數據，易得初始權矩陣。

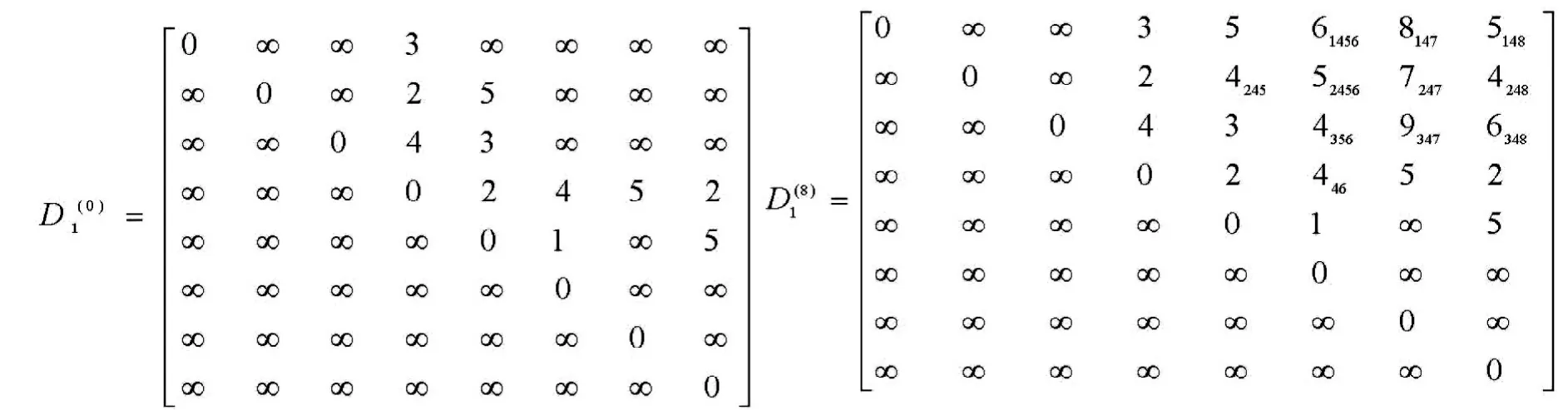
3.3 運用改進Floyd算法的網絡路徑優化

通過路徑仿真技術、先驗數據挖掘技術，結合C.M汽車裝配集團生產部進貨路線的特點，易知通過vi到vj路物流費用的綜合修正因子ij，并用lij+ij作為新的路權值，其變化情況如圖4所示。

1）基于傳統Floyd算法步驟，結合圖4數據，易得改進后的初始權矩陣。

圖4 改進后的裝配供應鏈賦權網絡路徑

3.4 兩種路徑選擇的比較

把基于傳統Floyd算法的進貨分配方案與基于改進Floyd算法的的進貨分配方案進行比較，可以看出：1）運用改進Floyd算法進行裝配供應鏈網絡路徑選擇時，可以避免出現兩種或多種方案都符合篩選條件，以致影響領導層的決策力；2）運用改進Floyd算法所得進貨方案是運用傳統Floyd算法所得進貨方案的子集，這樣可以縮小備選方案的數量，降低決策失誤的可能性；3）經過對vi到vj路物流費用的修正，所得綜合指標值更能體現現實情況。因此，改進后的進貨方案更有助于供應商、集配商以及裝配制造商之間的合作，從而間接地提高裝配供應鏈穩定高效的運行，最終實現整體收益大于各自單獨運營時所獲收益的總和。

4 結語

從供應鏈整體效益角度研究供應商、集配商和制造商所構成的裝配供應鏈最優網絡路徑選擇問題。綜合考慮三維虛擬動態聯盟網絡路徑選擇的影響因素，對傳統 Floyd算法進行改進，采用兼顧供貨提前期、物流質量以及物流成本的網絡路徑優化方案。實例分析表明，改進的 Floyd算法選擇最優網絡路徑更加貼近現實，從而保證裝配供應鏈穩健牢固運行。

總體而言，運用改進的 Floyd算法選擇最優網絡路徑，對裝配供應鏈的進一步研究具有一定的指導意義，對汽車、造船等企業具有一定的現實應用價值。但不可否認，對到路的物流費用的綜合修正因子的確定需進一步的研究。

[1]江玉杰.基于改進Shapley值法的裝配供應鏈收益分配研究[J].山東交通學院學報，2015(01)：36-40.

[2]劉振峰,陳燕.基于時間Petri網的供應鏈網絡關鍵路徑分析[J].數學的實踐與認識，2006(11)：32-37.

[3]陳岱蓮,李鵬.基于VRP模型的兩階段物流網絡路徑優化模型[J].重慶交通大學學報(自然科學版)，2009(06)：1131-1134.

[4]張旭鳳,張永安,楊麗.動態閉環復雜配送網絡路徑優化算法研究[J].中國流通經濟，2010(04)：34-37.

[5]曾云,劉宗武.基于復雜網絡理論的物流配送路徑優化研究[J].物流技術，2011(17)：113-114.

[6]劉家國,周粵湘,李俊,等.供應鏈彈性綜合優化路徑選擇模型分析[J].哈爾濱工業大學學報，2014(05)：101-106.

[7]樓振凱.基于Floyd算法的供應鏈網絡路徑研究[J].物流工程與管理，2014(05)：127-128.

[8]胡運權.運籌學教程（第二版）[M].北京:清華大學出版社,2003:226-228.

Research of Network Path Selection of Assembly Supply Chain Based on Floyd Algorithm Improvement

JIANG Yu-jie
(School of Business,Sanjiang University,Nanjing 210012,China)

This paper studies the network path selection of assembly supply chain from the overall efficiency on the chain by using Floyd algorithm.By taking the effect of the response speed,service quality and logistics costonnetworkpathintoconsideration,comprehensivecorrectionfactorshavebeenintroducedsoastoimprove the traditional Floyd algorithm.Based on the example analysis,the result shows that it is closer to reality and moreeconomicalto use theimprovedFloyd algorithmto choosetheoptimalnetwork path,which mayenhance the cooperation between each node in the chain of enterprises and finally realize the stable and efficient operation of assembly supply chain.

Floyd algorithm;assembly supply chain;network path selection

TP301.6

A

1674-2346(2015)04-0067-06

(責任編輯：田 犇)

10.3969/j.issn.1674-2346.2015.04.014

2015－08－23

江玉杰，男。研究方向：供應鏈管理