基于NUFFT的調頻步進頻高分辨成像與目標識別算法

向 寅張 凱 胡 程

(北京理工大學雷達技術研究所 北京 100081)

基于NUFFT的調頻步進頻高分辨成像與目標識別算法

向 寅*張 凱 胡 程

(北京理工大學雷達技術研究所 北京 100081)

雷達自動目標識別技術是發展未來智能化武器系統需首先突破的關鍵技術。相比于2維SAR圖像目標識別，基于高分辨距離像(HRRP)目標識別具有數據維度低、對雷達系統計算量和存儲量的要求低和成像算法簡單的優點。HRRP成像是目標識別中的前導和關鍵步驟，其速度和成像結果的質量好壞直接決定了目標識別的實時性和準確性。文中探討了一種新的HRRP成像算法–非均勻傅里葉變換(NUFFT)算法，推導并給出了用NUFFT進行調頻步進信號的回波模擬和高分辨成像的數學公式。同時通過分析成像算法各步驟的計算量，對4種成像算法的計算量進行了對比分析，并仿真了兩類地面目標成像與目標識別的結果。理論分析及仿真驗證都表明，該文算法的計算復雜度相對于其它算法均有不同程度的改善，可以有效地應用于雷達目標識別中。

雷達自動目標識別；高分辨距離像；調頻步進頻；高分辨率；非均勻傅里葉變換(NUFFT)

Reference format: Xiang Yin,Zhang Kai,and Hu Cheng. A NUFFT based step-frequency chirp signal high resolution imaging algorithm and target recognition algorithm[J]. Journal of Radars,2015,4(6): 639–647. DOI: 10.12000/JR15083.

1 引言

雷達自動目標識別(Radar Automatic Target Recognition,RATR)技術是指通過獲取并分析雷達發射并經過目標反射回來的電磁波特性，從中提取出所包含的目標屬性信息，從而自動識別目標的類型、類別[1]。在戰場日趨透明的現代信息化戰爭中，RATR系統可以實現目標類型、真假和屬性識別，完成戰略預警和戰場監視，從而對目標威脅度以及戰場全局環境有準確的預判，因此，RATR技術成為現代雷達技術的重要發展方向之一。

基于高分辨距離像(High Resolution Range Profile,HRRP)的目標識別由于其所含目標信息量豐富、對存儲量要求低、算法設計簡單等優點使其近幾年來越來越受到青睞。而調頻步進頻雷達信號通過發射一系列載頻線性跳變的調頻信號，將接收回波進行脈內脈沖壓縮及脈間IFFT的方法合成高分辨1維距離像，是一種重要的距離向高分辨信號形式。因其具有高的距離分辨率，同時又能大幅度降低信號處理機的帶寬需求等優勢，因此被廣泛用在雷達系統中。

頻率步進信號的信號處理算法，也即1維高分辨像成像算法的選擇決定了最終1維距離像的成像質量好壞，不同的信號處理算法有著各自的優缺點，目前較常用的高分辨成像算法有3類，分別是目標抽取算法[2–4]、時域合成算法[5]和頻域合成算法[6]。它們的計算流程及運算復雜度各不相同，但其共同本質都在于利用匹配濾波的原理得到場景的清晰1維像。本文在此基礎上，提出了一種快速匹配濾波1維高分辨像成像算法，利用匹配濾波原理使信噪比達到最優，用FFT快速算法進行計算，并利用Type-II型NUFFT快速算法一步完成從2維回波信號(脈內距離維，脈間頻率維)到1維高分辨距離像的脈沖壓縮高分辨成像過程，可以獲得滿意的處理結果。

為滿足實時處理需要，較低的算法復雜度是衡量成像算法好壞的重要因素。本文經過仔細分析與仿真驗證，論證了本文成像算法可以保證目標上各個散射中心的信噪比，并給出了算法的計算性能分析。

文章的最后采用雷達仿真數據驗證了理論分析的正確性。

2 非均勻FFT理論

傳統的傅里葉變換(FFT)算法要求輸入數據是等間隔采樣的，當輸入數據非均勻采樣時，傳統傅里葉變換算法失效。非均勻采樣快速傅里葉變換(Non-Uniform Discrete Fourier Transform,NUDFT)[7,8]是解決這一問題的有效手段，NUFFT算法是在非均勻分布的數據域內進行快速計算的一系列方法[9–15]。一類典型的問題是由給定的頻域N個非均勻采樣點重建對應的時域函數。非均勻傅里葉變換自從誕生以來，已經在很多領域得到應用，應用領域從醫學成像、射電天文學到求偏微分方程的數值解。本質上，NUFFT是FFT與插值運算的結合，其理論形式有兩種：一種是從非均勻采樣的域變到另一個均勻采樣域，另一個是其逆過程。在本文中，兩次用到NUFFT算法，一是調頻步進頻雷達回波的模擬，二是1維高分辨成像，因此在本節為簡單起見，將簡要介紹1-D 情況下的NUFFT算法原理。

傳統的DFT算法用數學語言描述如下：

當輸入數據在時域和頻域的采樣點都為N時，式(1)可用快速傅里葉變換算法來實現：

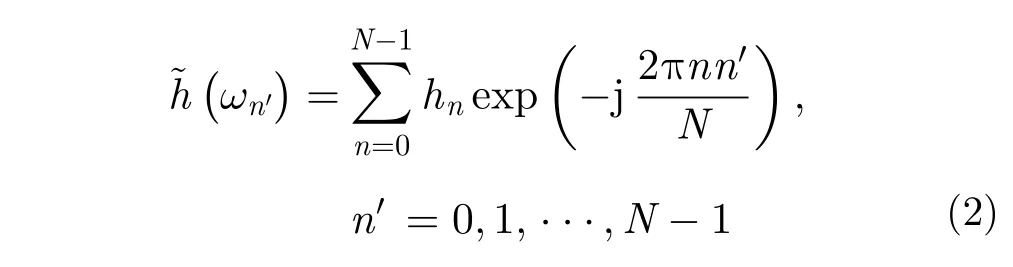
但是，在很多應用場合中數據是不等間隔采樣的，通常的FFT算法不再適用。非等間距傅里葉變換(NUDFT)是解決這一問題的有效方法，類似于FFT與DFT的關系，NUFFT是NUDFT的快速算法。它的精度取決于所用的窗函數的類型及長度。在這里我們用到的是Type-II型2-D 逆NUFFT快速算法，它是由非均勻的頻域采樣數據求解均勻時域采樣數據的過程。

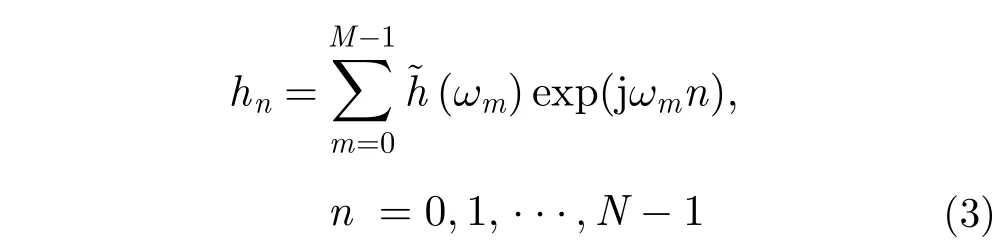
大多數NUFFT算法采用過采樣技術，由窗函數計算得出，這樣在時域和頻域都有很好的聚焦特性，因此，式(3)的計算步驟總結如下：

(1) 格網化(插值)：

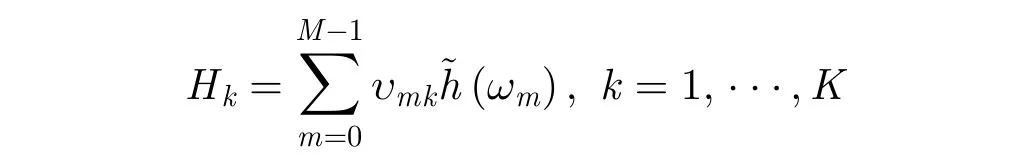
其中，υmk表示插值系數，此步驟需要O(JM)的計算復雜度，J 表示ωm附近的點數；

(2) K點DFT變換：

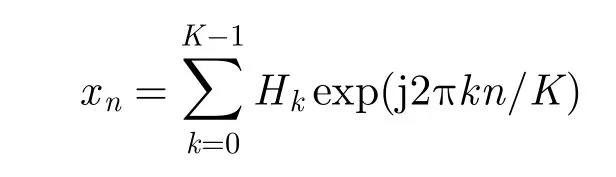
輸出信號xn為前N個信號值，此步驟需要O(Klog2N)的計算復雜度；

(3) 將xn用變標因子進行加權，其中sn是加權因子，“*”表示共軛操作，這樣就可以得到時域的均勻采樣數據hn。其中，常用到的變標因子有：余弦變標因子高斯變標因子三角變標因子等。

NUFFT總的算法復雜度為O(JM) +O(Klog2N)，通常選取K=2N 和J≤10。因此，NUFFT的算法復雜度除了一個常數項外與FFT相差不大，NUFFT算法更詳細的細節請參見文獻[14]。

3 基于NUFFT的快速匹配濾波成像算法

3.1 調頻步進頻雷達

調頻步進頻信號是一系列載波頻率等間隔線性跳變的線性調頻脈沖串。記單個基帶脈沖信號波形為：

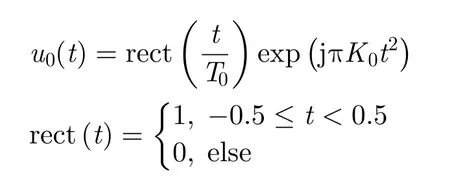
其持續時間為T0，調頻斜率為K0，帶寬B0=K0T0; fn=f0+nΔf,n=0,...,N-1為N個等間隔載頻，f0表示起始頻率，Δf表示跳頻間隔。若脈沖的發射間隔為Tr，則發射信號可以表示為：

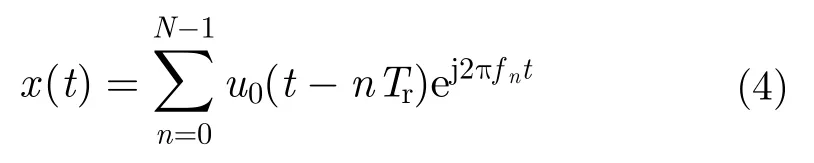
假設距離雷達位置為r處存在散射系數為σ0的靜止目標，則該目標的雷達回波可以寫成：

回波與本振信號混頻后得到基帶信號為：

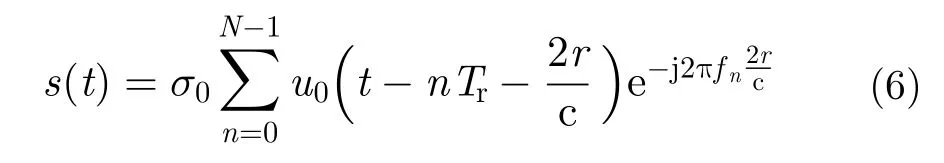
如果場景的后向散射系數為σ(r)，并把每個發射脈沖對應的回波記成sn(t)，則該場景對應的基帶回波可以寫成積分形式：

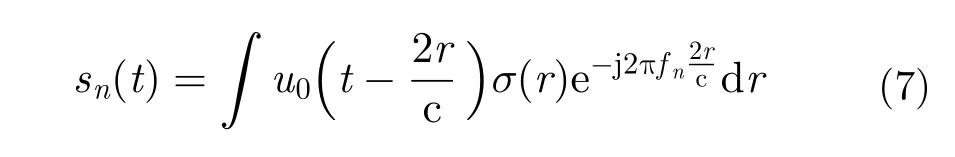
3.2 NUFFT高分辨成像算法

調頻步進頻雷達的回波是時-頻域的2維回波信號，其中脈內可看作場景的時域回波信號，脈間是載頻線性跳變的頻域信號。在將每個子脈沖變換到頻域并完成匹配濾波之后，由于兩個維度的采樣率不同，而最終所成的1維距離像(HRRP)是時域均勻采樣信號，因此由2維頻域回波數據到1維像的成像過程可以看作是由非均勻的頻域數據到均勻時域數據的非均勻傅里葉變換(NUDFT)，因此可以由NUFFT快速算法來實現。下面將從回波模擬與成像兩個過程介紹NUFFT調頻步進頻成像算法，兩個過程互為共軛。

(1) 步進頻回波模擬算子構建

式(7)為步進頻回波信號的簡單模型，其中積分核函數表征了步進頻雷達測量與目標場景后向散射率之間的線性依賴關系可以用線性算子A來表示。下面用NUFFT快速算法來求解式(7)的積分。

首先，對式(7)作傅里葉變換得到頻域表達式，

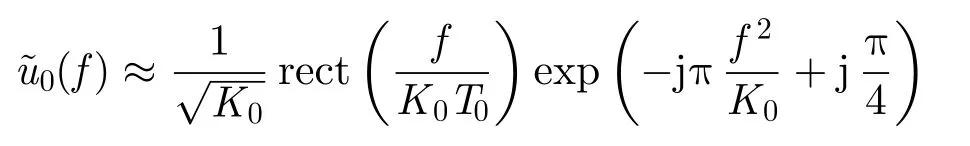
數據處理時通常用離散化來表示，令場景的距離分辨單元大小為Δr，距離像采樣坐標為rl=lΔr,l=0,1,...,L-1,σl=σ(rl)。令回波的頻域采樣間隔為Δfm，頻域采樣點可寫成fm=mΔfm,m=0,1,...,M-1。另記則式(8)的離散形式可表示成：

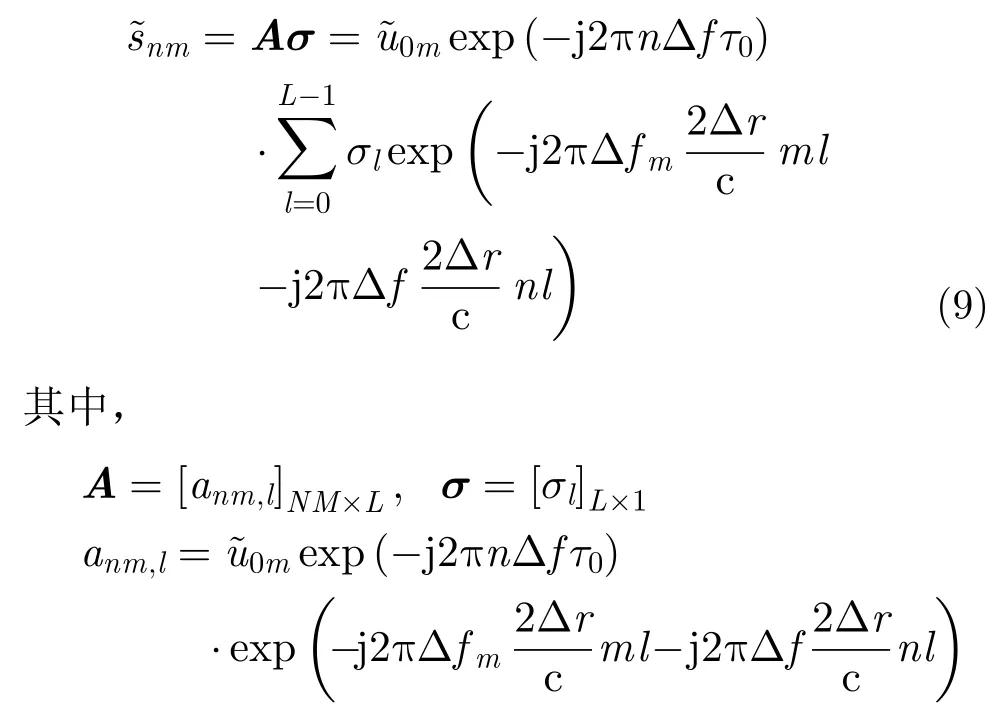
做如下變量替換：

即回波模擬算子可以利用2維非均勻傅里葉求和式(11)以及NUFFT算法快速實現。

對于靜止場景，頻率域仍然是均勻采樣，因此式(11)所描述的回波模擬算子只是實現了距離均勻采樣到快慢時間頻率域的快速插值操作。以此為基礎，可以擴展出非均勻頻率步進，或動目標場景步進頻成像的快速成像方法。

(2) 步進頻快速成像算子構建

回波模擬算子A的共軛算子AH，可以看做是成像算子，將式(9)進行共軛操作，可以得到場景的后向散射系數，也即目標RCS的計算公式：

從式(12)，也即式(9)取共軛運算的結果，可以看到其明顯的物理意義。下標為m的項表示每個子脈沖中的脈沖壓縮操作，下標為n的項表示脈間的IFFT操作。兩項合起來表示調頻步進頻信號的2維匹配濾波操作。同回波模擬過程相似，令

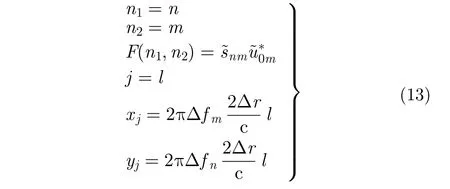
則線性算子A表示成了2-D NUFFT的形式：

即成像算子可以用式(14)以及NUFFT算法快速實現。

3.3 NUFFT及其計算復雜度

成像信噪比和計算復雜度往往是衡量成像算法好壞的兩個重要因素，下面從這兩個方面對新算法的性能進行評估。

根據第2節對NUFFT算法計算流程的分析，NUFFT成像方法的計算復雜度是數據維度以及加權函數長度的函數。因此，可以根據場景回波s~nm維度和成像算子的相關參數來評估算法的計算量。本小節將從算法的工作流程切入，對算法計算復雜度各組成部分進行分析。同時，在此基礎上，分析比對了新成像算法和傳統成像算法的復雜度。

從圖1可知，原始回波數據的脈內脈沖壓縮是4種算法共有的計算過程，因此為了計算量分析的方便，只比較4種算法其它計算步驟之間計算量的區別。假設雷達回波信號是P個子脈沖的回波，每個子脈沖回波進行N點采樣(粗分辨單元)。

(1) NUFFT方法

每個子脈沖內匹配濾波并變換到頻域，所需計算量O(PN+PNlog2N)；格網化(插值)所需計算量O(JP)，其中J=I(p)/p ; K 點IFFT所需計算量O(NKlog2I(p))；變標加權所需計算量O(NI(p)+I(p)Nlog2N)，總計算量為：

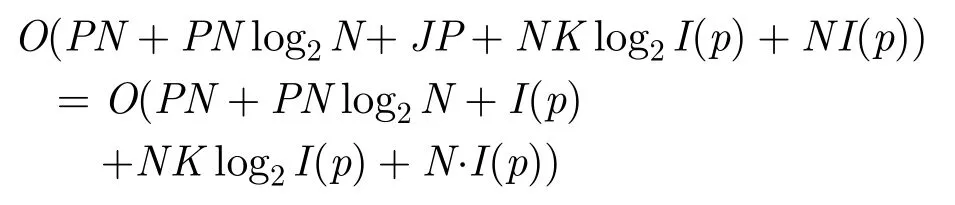
(2) 抽取拼接法

計算量主要在于IFFT步驟，為了快速計算，通常在每個粗分辨單元上做2的整數倍IFFT運算，因此先將每列P個數據補零成為2的整數倍。定義函數I(P)，其中若P為2的整數冪；若P為2的非整數冪；也即每列數據補零成I(P)個數據；整個算法的計算復雜度約為：

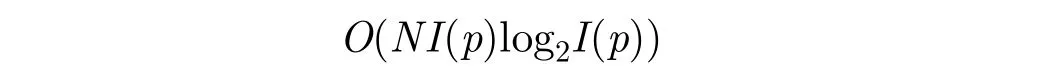
(3) 時域合成法

圖 1 4種算法的計算流程分析Fig. 1 Calculation flowchart of four algorithms

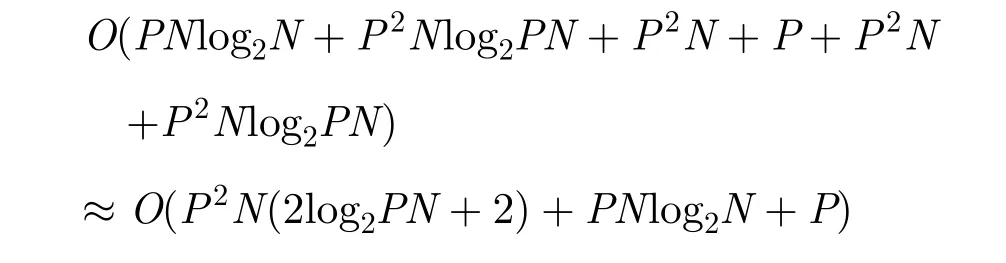
(4) 頻域合成法

頻域合成算法，各子脈沖做FFT得到頻譜以進行頻移和相參疊加，所需計算量O(PNlog2N)；構造濾波器H(f)進行幅度補償使各子脈沖的頻譜幅度成為理想矩形，所需計算量O(PN)；大帶寬信號做IFFT得到時域信號，所需計算量總計算量為：

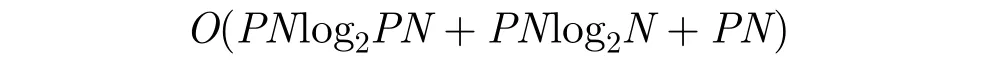
4種方法的計算量分析總結如表1所示。4種算法的計算量均為距離像采樣點數(N)和脈沖數(P)的函數，令距離向采樣點數在N=64～512，脈沖數在P=100～500之間變化，繪出其與計算量的函數關系曲線，如圖2所示。在NUFFT算法中，通常取K=2N,J≤10，在本文的應用中，K為比子脈沖數P大的2的整數次冪，即K=I(p)。

上述實驗結果表明計算量受數據維度的影響，而且隨著數據維度的增加成指數函數增加。在4種算法中，NUFFT、抽取拼接、頻域合成算法的計算量相當，均在107量級，時域合成算法的計算量最高，約為1010量級，這是由于其為避免頻譜混疊而進行的高倍升采樣操作造成的結果。

圖3(a)和圖3(b)分別給出了固定脈沖數和固定距離向采樣點數情況下計算量隨另一變量的函數關系曲線，對比4種算法的曲線可以發現抽取拼接算法的計算過程最簡單，因此計算量最低，本文的NUFFT方法和傳統的頻域合成方法計算量相當，甚至稍好于后者，而時域合成方法相比其它算法高出了近3個數量級。

表 1 4種算法的計算量比較Tab. 1 Computational complexity compare of four algorithms

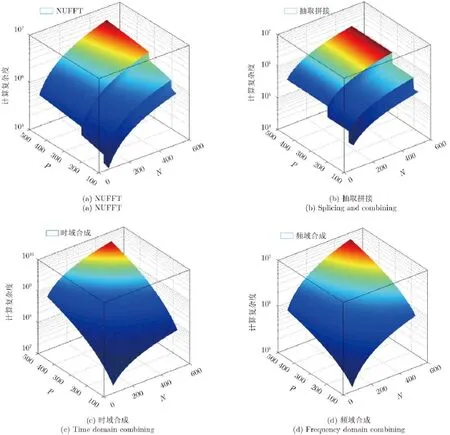
圖 2 4種算法的“計算量-采樣點數(N)-脈沖數(P)”曲線Fig. 2 Four algorithms “Computational complexity-sampling point (N)-pulse number (P)” curve

需要指出的是，圖3(b)中的階梯型函數是由于做I(p)列IFFT運算導致的，而在時域合成和頻域合成方法中，是將每個子脈沖在時域和頻域做合成操作處理，不涉及按列的脈沖間運算，因此不會仍然是一條平滑的對數函數曲線。在跳變點處，2的整數次冪點IFFT操作的目的是加快傅里葉變換的速度，但脈沖數(橫軸)的微小變化會導致計算量(縱軸)的成倍增加這一不利后果，實際中其最終效應是使得算法速度提升還是降低，有待于進一步論證。

4 仿真驗證

本節中利用仿真數據驗證本文所提方法的有效性。仿真中采用的線性調頻信號的參數為(表2)：脈沖寬度Tp=5 μs，調頻率信號帶寬B=30 Hz，相應的距離分辨率為5 m，依據奈奎斯特采樣定理，脈沖個數100，頻率跳變間隔6.25 MHz。在目標場景中放置M1坦克模型，其長約7 m，根據雷達波長與一般目標(飛機、坦克、艦船等)尺寸的相對大小關系，可知雷達工作在光學區。由散射中心理論可知，目標的散射可以等效為若干個散射中心組成的散射源。對于坦克目標，強散射中心的位置主要分布于炮筒前端、主炮與機身連接處、機身邊緣位置，其它部位如彈藥架、履帶等位置也可能產生若散射回波。將坦克建模為如圖4所示的主要散射點分布圖，散射中心的位置及幅度列于表2中，定義目標散射點的散射強度為歸一化幅度(從0～1不等)。雷達平臺位于目標正前方500 m處，雷達與目標均處于靜止狀態。

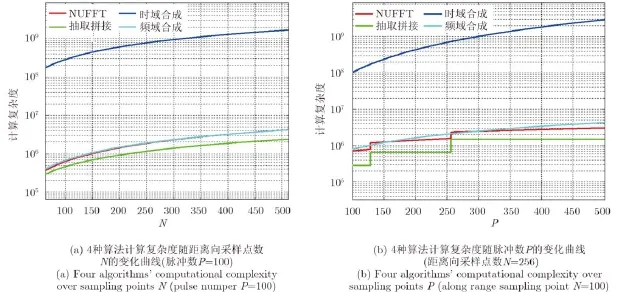
圖 3 計算復雜度分析Fig. 3 Analysis of the computational complexity

表 2 M1坦克主要散射中心位置與幅度分布Tab. 2 M1 tank main scattering points’ location and amplitude

采用NUFFT方法進行成像處理，其中主要參數的選取依據3.3節的分析，K=I(p),p=100～500,J=6，其最終1維高分辨像如圖5所示。

從圖4與實際算法成像結果圖5的對比中可以看出NUFFT成像算法的有效性，圖5中各散射點的位置和幅度列于表3中。對比表2與表3可以看出，NUFFT還原結果與仿真預設值基本吻合，誤差在2%～5%范圍內。該偏差是由于采樣峰值點的位置不在sinc函數的峰值處以及理想沖激函數的回波展寬導致的能量泄露引起的。

圖 4 目標主要散射點分布示意圖Fig. 4 Target's main scatter points distribution illustration

從圖5的成像結果中可以看到各個點目標的回波基本為一sinc函數，符合模型中對雷達回波進行脈沖壓縮的理論結果，個別點目標的旁瓣不對稱是由于相鄰散射點的影響所致。取104.8 m處的散射點2進行分析(圖6)可見，其第1副瓣水平約為–13.3 dB，同樣符合理想點目標的成像結果，且第2,第3旁瓣也與理想sinc函數吻合的較好，由此驗證了NUFFT方法在1維高分辨成像中的有效性。

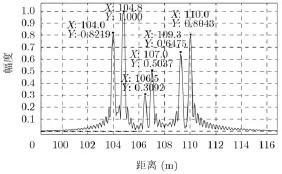
圖 5 目標場景1維高分辨像Fig. 5 HRRP of the target scene

表 3 成像結果各散射中心位置與幅度分布Tab. 3 Each scattering points’ location and amplitude in imaging result

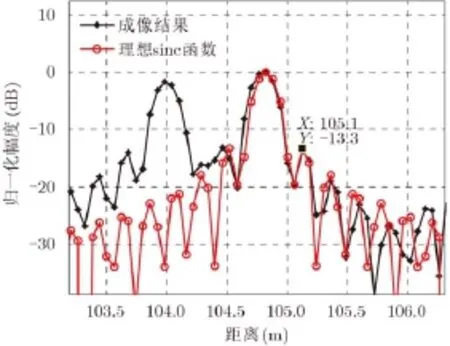
圖 6 104.8 m散射點成像結果與理想sinc函數對比Fig. 6 Comparison of imaging result and ideal sinc function of scattering point at 104.8 m

基于上述成像方法，為驗證此方法在目標識別中的有效性。本文仿真了兩類地面目標(M1坦克，防空單元)相對于雷達5種靜止姿態情況下(目標軸線與雷達視線方向夾角：迎頭(0°)、前斜(45°)、正側(90°)、后斜(135°)、尾追(180°)，見圖 7)的雷達回波，并用NUFFT方法快速成像，根據1維像的成像結果提取目標特征進行識別。

圖 7 M1坦克車和防空單元相對于雷達的5種姿態Fig. 7 Five positions of M1 tank and air defense units

用上文的仿真參數，對每種目標每個姿態各200幀的數據進行NUFFT成像，共產生11×200個 1維像，在成像結果的基礎上，提取目標散射點數和目標長度兩個特征進行分類識別。

如圖8所示，從目標的2維特征分布可以看出，兩類目標的各個姿態下由于其散射點和長度區分度較大，基本可以區分。但相同姿態不同目標的特征會有交叉重疊，類間區分度不大。需要提取目標其他特征進行輔助識別。

圖 8 目標散射點數–1維像長度2維特征分布圖Fig. 8 Target's scattering points–HRRP length 2-D diagram of distribution

5 結論

本文提出了一種基于非均勻傅里葉變換的調頻步進頻信號高分辨成像方法，利用非均勻快速傅里葉變換代替常規算法中復雜的時移、頻移等操作，有效降低了成像算法的計算復雜度，加快了信號處理的速度。理論分析與仿真實驗表明，基于非均勻快速傅里葉變換的快速成像算法能對目標場景進行清晰準確地成像，為后續的目標識別步驟提供了保障。

[1]Jacobs S P. Automatic target recognition using highresolution radar range profiles[D]. [Ph.D. dissertation],Washington University,1999.

[2]Long T,Li D,and Wu Q Z. Design methods for step frequency waveform and the target pick-up algorithm[J]. Systems Engineering and Electronics,2001,23(6): 26–31.

[3]Li D and Long T. Target's redundance removed algorithms of step frequency radar[J]. Acta Electronica Sinica,2000,28(6): 60–63.

[4]Long T,Han Y,and Mao E. Digital signal processing of stepped frequency radar[J]. Acta Aseronqutica et Astronautica Sinica,2001,22(S1): 16–25.

[5]Bai X,Mao S Y,and Yuan Y N. Time domain synthetic bandwidth methods: A 0.1 m resolution SAR technique[J]. Acta Electronica Sinica,2006,34(3): 472–477.

[6]Wilkinson A J,Lord R T,and Inggs M R. Steppedfrequency processing by reconstruction of target reflectivityspectrum[C]. Proceedings of the 1998 South African Symposium on IEEE Communications and Signal Processing,COMSIG'98,1998: 101–104.

[7]Potts D,Steidl G,and Tasche M. Fast Fourier Transforms for Nonequispaced Data: A Turorial[M]. Benedetto J J and Ferreira P,Modern Sampling Theory: Mathmatics and Applications,Boston: Birkhauser,2001: 247–270.

[8]Fessler J A and Sutton B P. Nonuniform fast Fourier transforms using min-max interpolation[J]. IEEE Transactions on Signal Processing,2003,51(2): 560–574.

[9]Dutt A and Rokhlin V. Fast Fourier transforms for nonequispaced data[J]. SIAM Journal on Scientific Computing,1993,14(6): 1368–1393.

[10]Liu Q H and Nguyen N. An accurate algorithm for nonuniform fast Fourier transforms (NUFFT's)[J]. IEEE Microwave and Guided Wave Letters,1998,8(1): 18–20.

[11]Nguyen N and Liu Q H. The regular Fourier matrices and nonuniform fast Fourier transforms[J]. SIAM Journal on Scientific Computing,1999,21(1): 283–293.

[12]Fessler J and Sutton B P. Nonuniform fast Fourier transforms using min-max interpolation[J]. IEEE Transactions on Signal Processing,2003,51(2): 560–574.

[13]Schaller S,Flohr T,and Steffen P. An efficient Fourier method for 3-D radon inversion in exact cone-beam CT reconstruction[J]. IEEE Transactions on Medical Imaging,1998,17(2): 244–250.

[14]Sarty G E,Bennett R,and Cox R W. Direct reconstruction of non-Cartesian k-space data using a nonuniform fast Fourier transform[J]. Magnetic Resonance in Medicine,2001,45(5): 908–915.

[15]Song J,Liu Q H,Kim K,et al.. High-resolution 3-D radar imaging through nonuniform fast Fourier transform (NUFFT)[J]. Communications in Computational Physics,2006,1(1): 176–191.

向 寅(1981–)，男，博士后，2010年于中國科技大學獲得博士學位，后在中國科學院電子學研究所任博士后，研究方向為壓縮感知、合成孔徑雷達成像和信號處理。

E-mail: xy_overlimit@sina.cn

張 凱(1989–)，男，碩士研究生，2015年3月獲得北京理工大學信息與通信工程專業工學碩士學位，研究方向為雷達目標識別。

E-mail: zhangkai3325@163.com

胡 程(1981–)，男，研究員，博士生導師，2003年7月獲得國防科學技術大學電子工程專業學士學位，2009年7月獲得北京理工大學目標探測與識別專業工學博士學位，在攻讀博士學位期間，于2006年3月至2007年5月赴英國伯明翰大學電子工程系進行為期15個月的訪問研究。2014年破格聘為研究員、博士生導師。主要研究方向為地球同步軌道SAR、地基SAR及新體制SAR成像與差分干涉處理技術。

E-mail: cchchb@163.com

A NUFFT Based Step-frequency Chirp Signal High Resolution Imaging Algorithm and Target Recognition Algorithm

Xiang Yin Zhang Kai Hu Cheng
(Institute of Radar Technology,Beijing Institute of Technology,Beijing 100081,China)

Radar Automatic Target Recognition (RATR) is the key technique to be breaked through in the fuure development of intelligent weapon system. Compared to the 2-D SAR image target recognition,High Resolution Range Profile (HRRP) target recognition has the advantage of low data dimension,low requirement of radar system's calculation and storage ability,and the imaging algorithm is also not complicated. HRRP imaging is the first and the key process in target recognition,its speed and imaging quality can directly influence the real-time capability and accuracy of target recognition. In this paper a new HRRP imaging algorithm – NUFFT algorithm is proposed,the derivation of mathematical expression is given,both for the echo simulation process and the imaging process. In the meantime,by analyzing each step's calculation complexity,we compared the calculation complexity of four different imaging algorithms,we also simulate two target's imaging and target recognition processing. Theoretical analysis and simulation both prove that the proposed algorithm's calculation complexity is improved in various degree compared with the others,thus can be effectively used in target recognition.

Radar Automatic Target Recognition (RATR); High Resolution Range Profile (HRRP); Stepfrequency chirp; High Resolution; NUFFT

The National Natural Science Foundation of China (61172177)

TN958

A

2095-283X(2015)-06-0639-09

10.12000/JR15083

10.12000/JR15083.

2015-07-02；改回日期：2015-12-09；網絡出版：2015-12-22

向寅 xy_overlimit@sina.cn

國家自然科學基金(61172177)

引用格式：向寅,張凱,胡程. 基于NUFFT的調頻步進頻高分辨成像與目標識別算法[J]. 雷達學報,2015,4(6): 639–647.