用于調制寬帶轉換器壓縮頻譜感知的重構失敗判定方法

鄭仕鏈 楊小牛

1 引言

認知無線電頻譜感知需要對很寬的頻段進行頻譜檢測[1]。在 Shannon采樣理論下，要瞬時覆蓋寬頻段往往需要多路模數轉換器，硬件實現較為復雜。壓縮采樣（也稱為壓縮感知）則有望以低于 Nyquist采樣率的速率完成寬頻段采樣[2]，因此，很多學者將壓縮采樣應用到寬帶頻譜感知中[37]-。目前針對模擬信號的壓縮采樣方式主要有兩種：隨機解調采樣[8]以及調制寬帶轉換器（Modulated Wideband Converter, MWC）采樣[9]。隨機解調采樣假設信號滿足多音模型，而MWC采樣的信號模型為多子帶信號模型，與實際情況更為接近[10]。本文的研究針對MWC采樣。

在 MWC采樣應用于頻譜感知方面，文獻[11]中給出了一些實驗結果，文獻[12]將文獻[11]的工作進行擴展，提出了一種更為詳細的基于MWC采樣的寬帶頻譜感知流程，并給出了仿真結果。文獻[13]進一步討論了MWC壓縮采樣后的循環平穩檢測方法。壓縮采樣得以應用的前提條件是信號的稀疏性，MWC也不例外。將MWC采樣應用于頻譜感知的一個基本前提就是頻譜的稀疏性，即只有很少一部分的子信道被主用戶占用。一旦確定了MWC采樣系統的參數，其所能接受的頻譜稀疏程度也就確定。但是，由于無線頻譜環境的復雜性，并不能保證待感知的頻段一定滿足MWC的稀疏度要求。因此，信號不稀疏的情況下，頻譜感知結果無法保證正確，若相信該結果而利用“頻譜空穴”，則會對主用戶造成干擾。針對該問題，文獻[14]提出了通過多個認知節點相互協作來判斷重構是否成功。由于需要多個節點協作，增加了信息交互量和實現復雜度。本文則提出一種只需單個認知節點的MWC壓縮采樣重構是否成功的判定方法，認知節點自身通過連續兩次重構結果之間的相關性來判斷重構結果是否值得信賴（即稀疏度是否在 MWC采樣系統的接受范圍內）。本文方法無需節點間的協作，降低了信息交互負擔，可以避免在信號不稀疏的情況下相信重構結果，因此能夠降低對主用戶的干擾，達到保護主用戶的目的。

2 MWC壓縮采樣

MWC采樣[9]框圖如圖1所示。具體來講，信號x（ t）同時輸入m個通道。在第i個通道，信號 x（ t）與周期為 Tp的混頻函數相乘，接著通過一個截止頻率為1/（2Ts）的低通濾波器，濾波后的信號以1/Ts的速率進行采樣。由于1/Ts足夠小，所以現有的商用ADC能用來完成采樣過程。

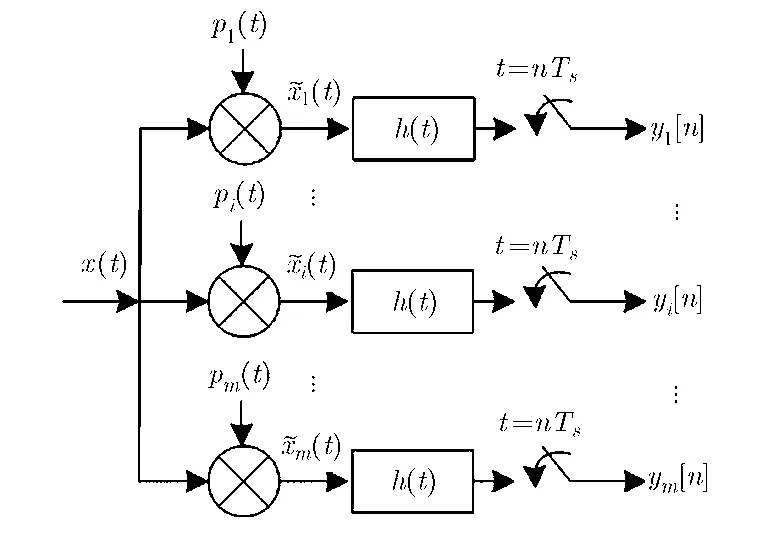
圖1 MWC采樣框圖

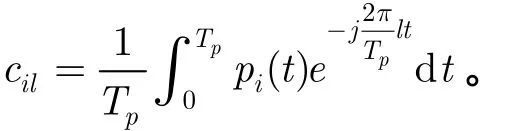
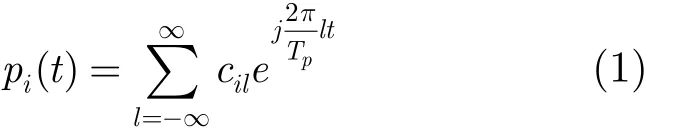
其中，考慮所有m個通

道，有式（2）形式的表達式成立[9]：

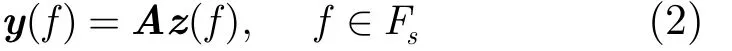
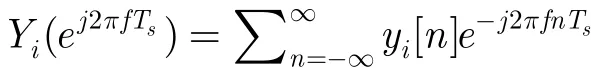
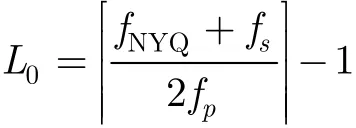
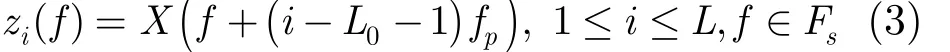
其中（）X f為（）x t的Fourier變換。mL×矩陣A第i行第l列元素ila 為

給定A和y（f），通過求解式（2），可以得到未知的z（f），再根據式（3）的關系式，可以求得原信號X（ f）。由于M＜L，所以式（2）所示的問題為欠定問題，當未知矩陣滿足稀疏性條件時，可以采用壓縮感知領域的重構方法來求解。

文獻[9]中提出如下過程進行重構，首先計算：

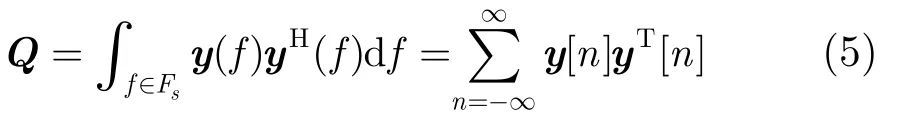
s通道采樣構成的采樣向量，然后得到滿足 Q =VVH的矩陣V。接著通過求解 V = AU得到U的支撐S= s upp（U ） ，由于U的支撐與 z（ Fp） 相等，由此也就得到了 S = s upp（z （ Fp））。得到S后，就可以計算得到各個子帶信號：

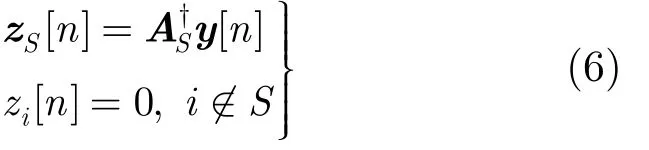
3 重構失敗判定方法

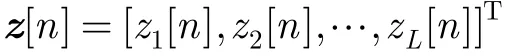
本文提出判斷重構成敗的方法基于頻譜環境相對于重構時間來說是慢變的基本思想，由此，如果重構成功，那么相鄰兩次重構得到的信號的頻譜應該非常接近一致，對應的各個子帶信號的能量也應該接近一致；而如果重構失敗，那么由于算法的隨機性，相鄰兩次重構得到的信號的子帶能量會有很大差別。因此，可以利用連續兩次重構所得信號子帶能量之間的相關性對重構成敗進行判決。

設 S1和 S2分別表示連續兩次重構得到的支撐，z（1）[n]和 z（2）[n]分別表示連續兩次重構得到的子帶信號。計算各個子帶能量：

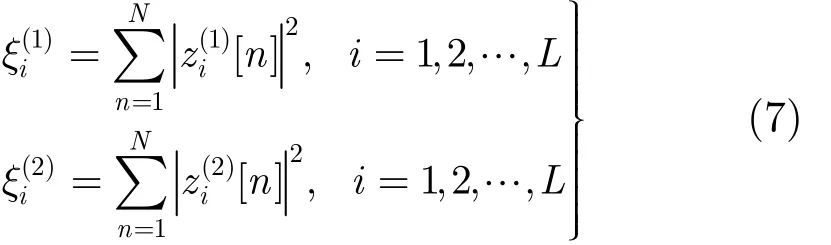
接下來計算判決統計量：

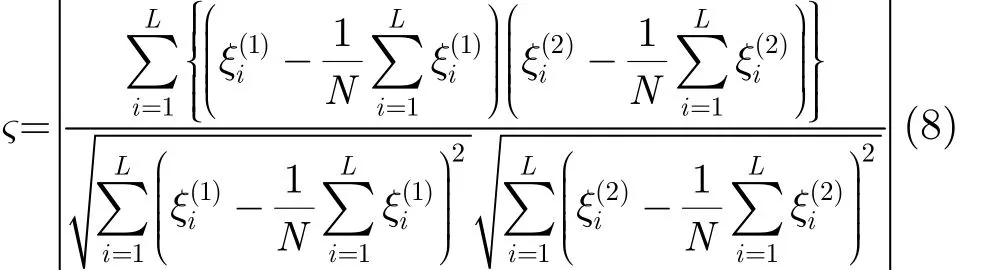
綜上所述，本文提出的MWC壓縮采樣重構成敗的判定方法流程如下：

Q = VVH的矩陣V，求解 V = AU得到U的支撐S1= s upp（U ） ，按式（6）計算得到子帶信號 z（1）[n]；

步驟 4 根據式（8）計算得到判決統計量ζ。如果ζγ＞，判定重構成功（對應于信號稀疏），否則，判定重構失敗（對應于信號非稀疏），γ為判決門限。

經過以上步驟，如果判定重構失敗，則認為頻譜感知結果不可信，認知用戶不利用任何頻譜空穴，以避免對主用戶造成干擾。如果判定重構成功，則相信頻譜感知結果。

本文方法依賴于相鄰兩次重構結果，從重構計算復雜度上來看，是單次重構方法的兩倍。除重構之外，本文方法還需要式（7）所示的能量計算和式（8）所示的相關運算，計算復雜度為（）O NL。

4 仿真結果分析

仿真參數設定如下：信號頻段 0～525 MHz,m= 4 0, fs= fp= 6 MHz。這種參數配置下，MWC系統總的采樣率為 240 MHz，遠遠低于Nyquist采樣率1050 MHz。仿真中，支撐重構算法考慮求解多觀測向量模型的正交匹配（Orthogonal Matching Pursuit, OMP）算法[15]以及聚焦欠定系統求解法（FOCal Underdetermined System Solver,FOCUSS）[16]兩種方法。主用戶信道數目為87，各個信道上的主用戶信號為BPSK或QPSK調制的通信信號，碼速率共有4種取值可能：1.5 ksps（symbol per second）, 2.0 ksps, 2.5 ksps和 3.0 ksps。基帶成型濾波器采用升余弦濾波器。整個頻段上的信號信噪比固定為30 dB。

圖 2中直觀給出了兩種情況下（稀疏和不稀疏）兩次重構得到的各個子帶能量，其中圖2 （a）中信號個數為4，圖2（b）中信號個數為20。由圖2可知，當信號個數為4時，滿足頻域稀疏條件，兩次連續重構得到的信號子帶能量非常接近，其相關性達到了0.9990；而當信號個數為20時，已經超出了重構所能支持的稀疏度，因此兩次連續重構得到的信號子帶能量差異較大，相關性僅為0.7526。由此可知，兩次連續重構所得子帶能量之間的相關性可以反映重構是否成功。

圖 3給出了本文方法對重構成敗的判斷準確率，其中判決門限γ設定為 0.993，圖中同時給出OMP重構概率。判斷準確率由本文方法判斷重構成敗結果與第 2次重構實際成敗的比對得到，即第2次實際重構失敗且本文方法判定重構失敗的概率與第2次實際重構成功且本文方法判定重構成功的概率之和。第2次重構實際上是否成功采用支撐集來衡量：重構所得的支撐集合中包含所有被占用的信道標號，則實際重構成功，否則，實際重構失敗。圖3中重構概率即按照第2次重構實際成功的次數與仿真次數（本實驗中為500）的比值來描繪。由圖3可知，隨著主用戶信道占用數目的增加，頻譜變得越來越不稀疏，因此，OMP重構概率越來越小。在信道占用數目為15和16附近時，本文方法對重構成敗的判斷準確率有所降低，這是因為在信道占用數目為15和16附近時，重構概率在0.5附近，實際重構成敗的不確定性最大，前后兩次重構結果成敗的不一致性也最大，而由于本文重構成敗的判定方法依賴于前后兩次重構結果的相關性，因此導致其準確率降低。在信道占用數目較小（例如小于 10）或較大（例如大于 20）時，本文方法對重構成敗的判斷準確率都非常接近于 1，說明了本文方法的有效性。

圖4給出了不同門限下本文方法對重構成敗的判斷準確率，采用 OMP方法。由圖可知，判決門限的選擇對判斷準確率有影響，其值選擇太小會造成判斷準確率的降低，但也不能選擇過大，太接近1會導致在信號不稀疏時判斷不準確。從圖4中結果可以看出，0.995是較為合適的選擇。圖5給出采用 FOCUSS方法作為重構方法時本文方法的判斷準確率，判決門限采用0.995。從中可以看出，性能與OMP情況相當。

圖6給出了利用頻譜感知結果造成的對主用戶的干擾概率，采用 OMP算法作為重構方法，FOCUSS的結果類似，為了簡潔起見，在此省略其結果。干擾概率定義為被干擾的主用戶信道數與總的被占用的主用戶信道數目的比值。由圖6可知，本文方法很好地避免了對主用戶的干擾，對保護主用戶的正常工作來說具有重要意義。

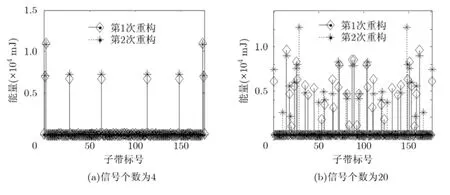
圖2 子帶能量

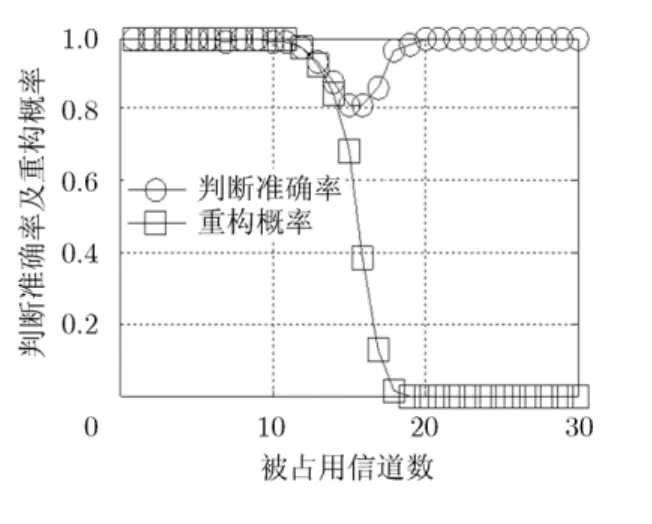
圖3 判斷準確率及重構概率（OMP）

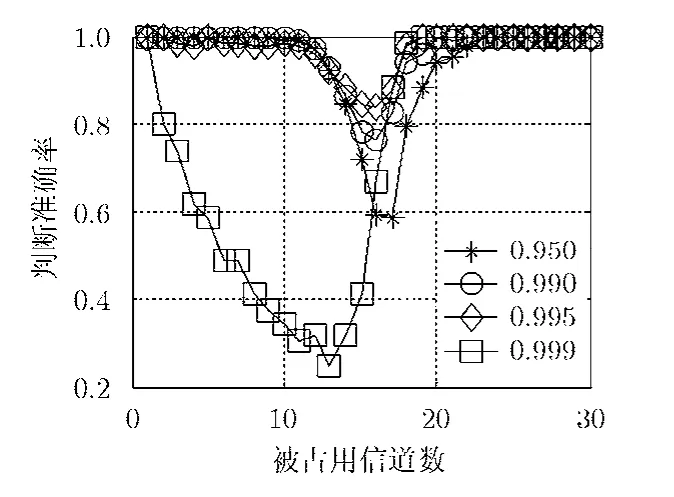
圖4 判斷準確率（OMP）

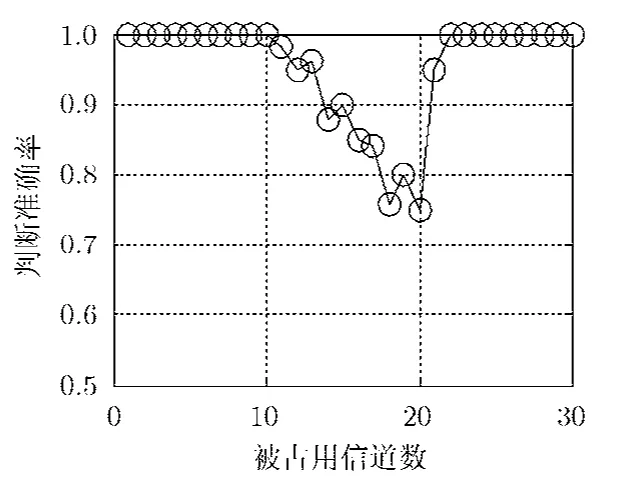
圖5 判斷準確率（FOCUSS）

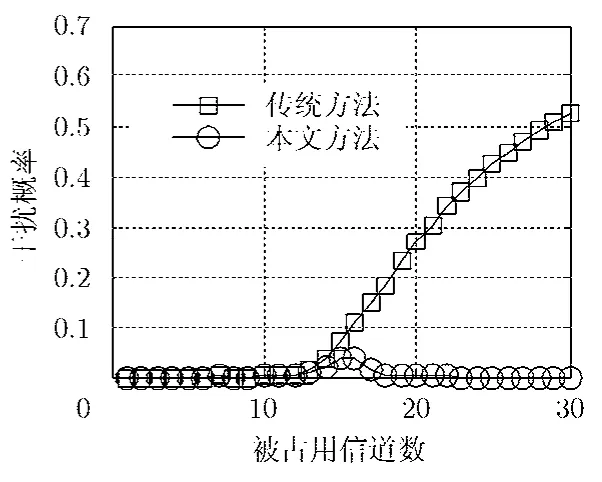
圖6 主用戶干擾概率

5 結束語

MWC壓縮采樣應用于頻譜感知的一個前提是信號在頻域上的稀疏性。如果信號不稀疏，將導致MWC重構結果不正確，此時若相信重構結果進而利用誤判的頻譜空穴，則會對主用戶造成干擾。本文提出了一種判斷MWC壓縮采樣重構是否成功的方法，以此解決認知無線電頻譜感知應用中頻譜不稀疏時重構結果不可靠導致的對主用戶的干擾問題。仿真中采用了OMP和FOCUSS兩種方法。結果表明在重構算法重構概率接近于1或接近于0對應的稀疏度區域，本文方法能夠非常準確地判斷MWC壓縮采樣重構成敗，判斷準確率接近1。在重構概率為 0.5附近對應的稀疏度區域，本文方法性能有所降低。另外，本文方法能夠顯著降低在頻譜不稀疏時對主用戶的干擾概率，從而達到保護主用戶的目的。后續研究需要進一步改進重構概率為0.5附近對應的頻譜稀疏度時的判斷準確率。

[1] Sun H, Nallanathan A, Wang C X, et al.. Wideband spectrum sensing for cognitive radio networks: a survey[J]. IEEE Wireless Communications, 2013, 20（2）: 74-81.

[2] Donoho D. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52（4）: 1289-1306.

[3] Tian Z, Tafesse Y, and Sadler B M. Cyclic feature detection with sub-Nyquist sampling for wideband spectrum sensing[J].IEEE Journal of Selected Topics in Signal Processing, 2012,6（1）: 58-69.

[4] Sun H, Chiu W Y, and Nallanathan A. Adaptive compressive spectrum sensing for wideband cognitive radios[J]. IEEE Communications Letters, 2012, 16（11）: 1812-1815.

[5] Yen C P, Tsai Y, and Wang X. Wideband spectrum sensing based on sub-Nyquist sampling[J]. IEEE Transactions on Signal Processing, 2013, 61（12）: 3028-3040.

[6] Romero D and Leus G. Wideband spectrum sensing from compressed measurements using spectral prior information[J]. IEEE Transactions on Signal Processing, 2013, 61（24）:6232-6246.

[7] Bai L and Roy S. Compressive spectrum sensing using a bandpass sampling architecture[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012,2（3）: 433-442.

[8] Tropp A, Laska N, Duarte F, et al.. Beyond Nyquist: efficient sampling of sparse bandlimited signals[J]. IEEE Transactions on Information Theory, 2010, 56（1）: 520-544.

[9] Mishali M and Eldar Y C. From theory to practice:sub-Nyquist sampling of sparse wideband analog signals[J].IEEE Journal of Selected Topics in Signal Processing, 2010,4（2）: 375-391.

[10] Mishali M, Eldar Y C, and Elron A J. Xampling: signal acquisition and processing in union of subspaces[J]. IEEE Transactions on Signal Processing, 2011, 59（10）: 4719-4734.

[11] Mishali M and Eldar Y C. Wideband spectrum sensing at sub-Nyquist rates[J]. IEEE Signal Processing Magazine, 2011,28（4）: 102-135.

[12] Zheng S and Yang X. Wideband spectrum sensing in modulated wideband converter based cognitive radio system[C]. The 11th International Symposium on Communications and Information Technology, Hangzhou, China, 2011:114-119.

[13] Cohen D, Rebeiz E, Jain V, et al.. Cyclostationary feature detection from sub-Nyquist samples[C]. The 14th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, San Juan, Puerto Rico,2011: 333-336.

[14] Zhang Z, Li H, Yang D, et al.. Collaborative compressed spectrum sensing: what if spectrum is not sparse[J].Electronics Letters, 2011, 47（8）: 519-520.

[15] Tropp J and Gilbert A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53（12）:4655-4666.

[16] Cotter S F, Rao B D, Engan K, et al.. Sparse solutions to linear inverse problems with multiple measurement vectors[J].IEEE Transactions on Signal Processing, 2005, 53（7）:2477-2488.