FAST饋源艙精調機構位姿測量系統性能分析

詹銀虎，鄭 勇，張 超，張中凱

(信息工程大學導航與空天目標工程學院，河南鄭州450052)

一、引 言

FAST(five hundred meter aperture spherical radio telescope)是500 m口徑球面射電望遠鏡的簡稱，是中國貴州省正在建設的世界上最大的單口徑射電望遠鏡［1］。饋源艙是FAST工程的核心部件之一，在天文觀測運行中，饋源艙由6根鋼索概略拖動至反射面焦點，再通過精調機構微調，實現饋源高精度的定位和指向跟蹤(如圖1所示)。FAST饋源測量系統的一項艱巨任務是:在500 m跨度的鋼索結構上，對饋源艙精調機構的實時動態定位精度達到4 mm，定姿精度達到1°，并將測量結果實時反饋給控制系統，實現閉環控制［2］。

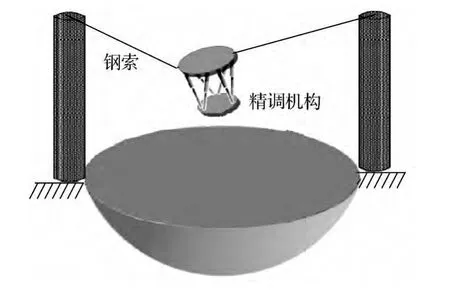
圖1 饋源艙、精調機構簡圖

由于激光跟蹤儀測程有限，攝影測量易受外界環境干擾且動態識別實時處理困難，GPS動態測量精度較低，目前提出的精調機構位姿測量方案中，主要考慮全站儀測量系統［3］。該系統由位于反射面內測量基準點上的全站儀、位于精調機構下平臺邊緣的目標棱鏡、測量控制及數據處理系統、供電通信線路等組成。在測量實施時，由測量控制系統控制全站儀照準對應的目標棱鏡進行測量，獲得動態測量數據，并由數據傳輸線傳給數據處理系統，通過全站儀動態測量數據處理軟件實時處理獲得棱鏡的點位坐標。本文介紹了全站儀測量系統的組成和測量方案，著重對系統的測量條件進行了計算和分析，并通過仿真測量，分析了系統所能達到的定位和定姿精度，以及系統的可靠性。

二、測量系統組成及測量方案

1.測量基準網

如圖2所示，中性反射面的口徑約為500 m，測量基準網由均勻分布于反射面內的24個基準點(JD-0～JD-23)組成，目前基準點的點位坐標已經固化。其中，JD-0～JD-5位于反射面底部中心的正五邊形頂點和中心;JD-6～JD-11近似均勻分布在水平半徑約110 m的圓周上;JD-12～JD-23近似均勻分布在水平半徑約210 m的圓周上，但個別基準點的位置有所調整。如JD-15的位置已調整至反射面的邊沿，其距離反射面中心的水平距離約為250 m，是較為特殊的一個控制點。

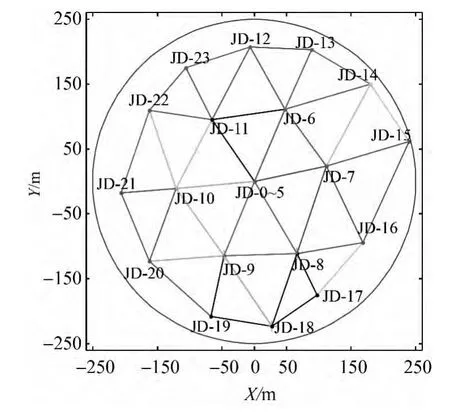
圖2 測量基準網的平面布設圖

2.全站儀

如圖3所示，用于精調機構位姿測量的全站儀共有9臺，分別安置在JD-13～JD-15、JD-17～JD-19、JD-21～JD-23的9個基準點上。在測量實施時，由測量控制系統控制全站儀照準對應的目標棱鏡進行測量，獲得實時動態測量的距離和角度數據，并由數據傳輸線傳給數據處理系統。

圖3 全站儀測量系統示意圖

3.目標棱鏡

如圖4所示，用于精調機構位姿測量的目標棱鏡共有9個，分別安置在精調機構下平臺邊緣的9條棱上。為了提高測量精度，目標棱鏡將采用高精度的角錐棱鏡。

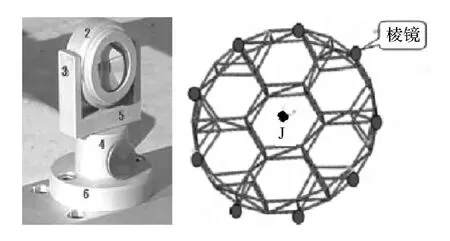
圖4 目標棱鏡示意圖

由于棱鏡跟隨精調機構的最大運動速度為11.6 mm/s，全站儀進行動態跟蹤測量時，必須解決時間同步的問題。目前，衛星授時、計算機守時技術比較成熟，且全站儀測量時滯的檢定精度可達0.02 s，可滿足 FAST 對時間同步精度的要求［4］。

4.測量流程

1)由測量控制系統向全站儀發送各種工作指令。

2)全站儀按照動態測量模式運行，一臺全站儀跟蹤一個事先確定的棱鏡，進行距離和角度測量，連續獲得棱鏡中心的距離和水平角、垂直角觀測量，并發送給數據處理系統。

3)數據處理系統對每臺全站儀的測量數據進行實時處理，獲得每個棱鏡的瞬時位置，進而由9個棱鏡的位置計算出精調機構的瞬時位置、姿態和對應的時間等信息，并發送給全站儀測量控制系統。

4)全站儀測量控制系統將數據處理結果發送給測量總控系統。

三、系統測量條件計算和分析

系統測量條件主要有棱鏡入射角、全站儀觀測距離和觀測高度角。棱鏡入射角與棱鏡面的法向指向有關，觀測距離和觀測高度角與棱鏡的空間位置有關。而在FAST運行過程中，棱鏡將跟隨精調機構做整體運動。因此，系統的測量條件由精調機構的空間位置和姿態間接決定。

1.精調機構的空間位置和姿態

如圖5所示，球形反射面的口徑約為500 m，測量坐標系原點O位于反射面的球心，Z軸指向天頂，X軸指向東，Y軸與X、Z軸構成右手系。陰影部分表示有效照明口徑內的反射面，呈瞬時拋物面型，Or為拋物面頂點，O為中性反射面的球心［5］。則在理想狀況下，精調機構通過一次索驅動的粗略調整，以及自身的精確微調，可以使其中心J到達拋物面的焦點Of，指向為z=OrO。當反射面的有效照明口徑不斷變換時，饋源精調機構的位置不斷變化，其運動范圍構成一球冠軌跡。該球冠軌跡半徑r≈162.9 m，最高點H距離O點的水平極距約為100 m，即從Z軸方向看精調機構，其平面運動范圍約為半徑100 m的圓。

2.棱鏡的位置和指向

如圖5所示，設饋源位于球冠軌跡的底部中心L時，某棱鏡Pi在測量坐標系下的位置為pi，棱鏡面的法向(即棱鏡的指向)為ni。由于精調機構在6根鋼索的牽引下運動時，自旋運動較小，對棱鏡入射角、觀測距離和觀測高度角的統計影響可以忽略，因此，精調機構中心由L點運動到Of點的過程，可等效簡化為2個步驟:①精調機構沿方向由L點平移至Of點;②精調機構在Of點，以a=z×Z為軸旋轉θ［6］。則Of點的棱鏡的位置矢量p'i和指向ni'可表示為

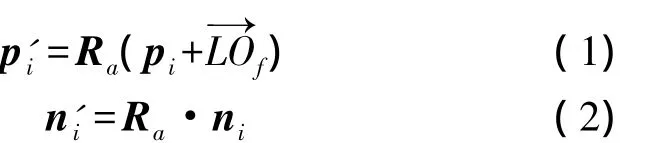
Z=［0 0 1］T，即測量坐標系Z軸方向的單位矢量。式(1)和式(2)中的Ra為繞a軸的旋轉矩陣，關于Ra的求解，國內外諸多學者進行了廣泛而深入的研究，求解方法基本可歸納為四元數法、旋轉矩陣法、歐拉角法［7-10］。本文采用的是文獻［10］的方法。

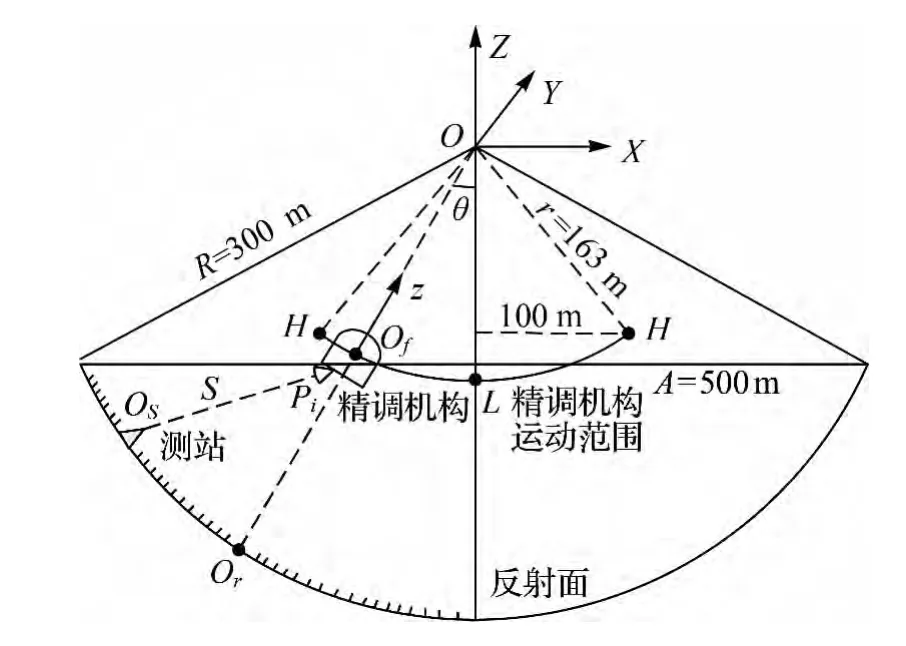
圖5 精調機構的空間位姿

3.測量條件的計算方法

如圖5所示，由測站Os觀測精調機構上的某棱鏡Pi。用S表示觀測矢量，則

式(3)中Os為測站點的坐標，為已知值。棱鏡入射角α、觀測距離d，以及觀測高度角h可表示為

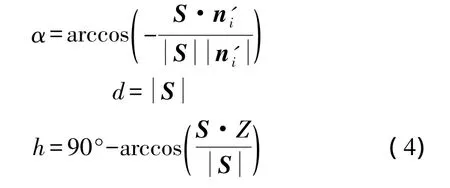
四、系統測量條件計算和分析

考慮到反射面內最外圍控制網的12個測站具有一定的對稱性，且精調機構的運動范圍也具有對稱性，因此只需要挑選具有代表性的測站統計棱鏡入射角、觀測距離和觀測高度角即可。下面挑選了JD-15和JD-21兩個基墩，JD-15的位置靠近反射面的邊沿，位置較為特殊;JD-21距離反射面中心的水平距離約為210 m，同其他控制點的位置基本一致，具有代表性。

1.棱鏡入射角

圖6是以JD-15測站為例，計算測站與對應的觀測棱鏡之間的入射角。圖中用顏色表示入射角的大小。

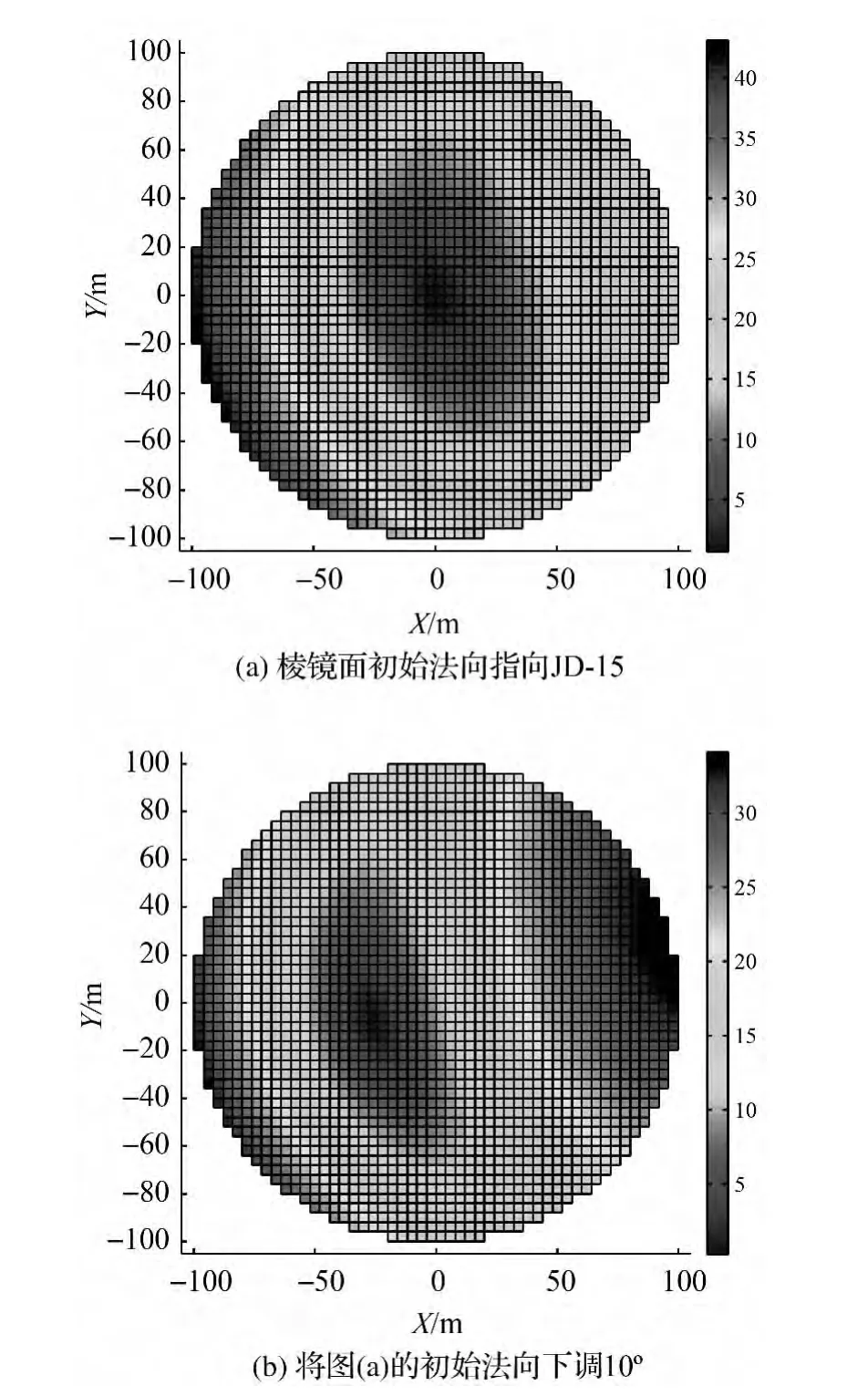
圖6 棱鏡初始指向與全局入射角的關系

定義精調機構位于L點時的棱鏡面法向為初始法向，圖6(a)是棱鏡的初始法向指向測站時，全局范圍內的棱鏡入射角統計情況。其中入射角最大值小于 45°，平均值為 19.0°;圖 6(b)是在圖 6(a)的基礎上將棱鏡面的初始法向向下調整10°之后，全局范圍內的棱鏡入射角統計情況。其中入射角最大值約為35°，平均值為18°。顯然，棱鏡面的初始法向下調整大約10°后，棱鏡入射角得到了全局改善。對于不同的測站，若要保證相應觀測棱鏡的入射角全局最優，需要對棱鏡的初始法向進行不同幅度的調整。經過對每個測站的計算分析，表1給出了9個測站的棱鏡入射角最優統計結果。

文獻［11—12］研究指出，利用棱鏡進行激光測距時，棱鏡的有效反射面積隨入射角增大而減小，進而影響測距精度。當入射角達到35°時，激光測距誤差約為0.05 mm;而入射角在20°以內時，測距誤差小于0.01 mm;入射角在15°以內時，測量精度最高，穩定性最好。因此，相對于精調機構4 mm的定位精度要求，因棱鏡入射角產生的測距誤差可以忽略。文獻［13］研究了棱鏡入射角對測角精度的影響，并通過試驗給出了經驗改正公式，改正后的測量點位坐標誤差小于1 mm。

表1 棱鏡入射角統計(°)

對于單個棱鏡而言，因棱鏡入射角偏大可能引入系統性的定位誤差;但對9個棱鏡而言，這一系統誤差可能呈現一定的隨機性，可通過最小二乘法等數據處理方法予以減弱。

2.觀測距離

圖7、圖8顯示了JD-15測站和JD-21測站的測距變化范圍。JD-15測站的測距變化范圍約為150～350 m，JD-21測站的測距變化范圍約為140～320 m。全站儀動態測距精度約為2 mm+1×10-6D，因此可以估算測距精度的變化范圍約為2.1～2.4 mm。

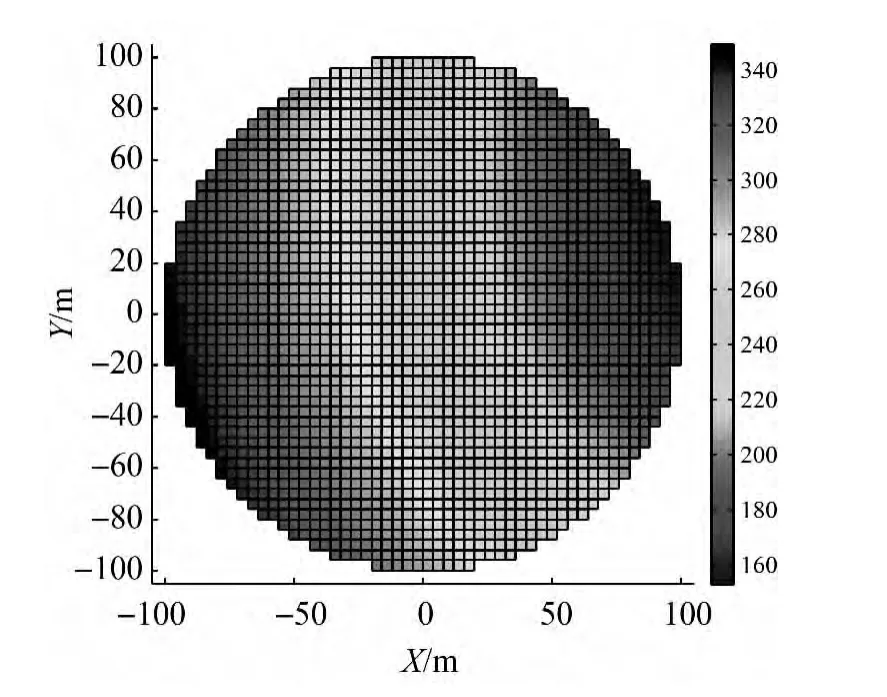
圖7 JD-15測站的測距變化范圍

3.觀測高度角

圖9、圖10顯示了JD-15棱鏡和JD-21測站觀測高度角變化范圍。由于JD-15測站更靠近反射面邊沿，因此其觀測棱鏡時的高度角偏小，最大值約為15°，最小值接近0°;JD-21測站相對靠近反射面中心，因此其觀測棱鏡時的高度角偏大，最大值約40°，最小值約為15°。因此，在饋源的整個運行軌跡上，觀測高度角的分布比較合理，可兼顧水平和高程方向的精度控制。此外，較低的觀測高度角有利于工程實踐中全站儀的防護。

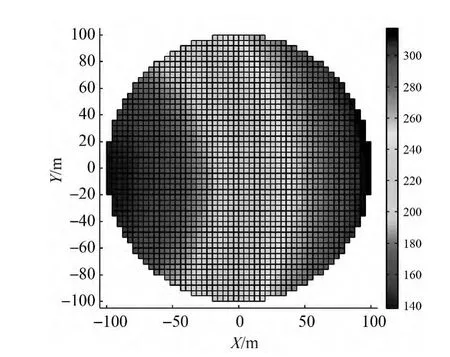
圖8 JD-21測站的測距變化范圍

圖9 JD-15測站的高度角變化范圍

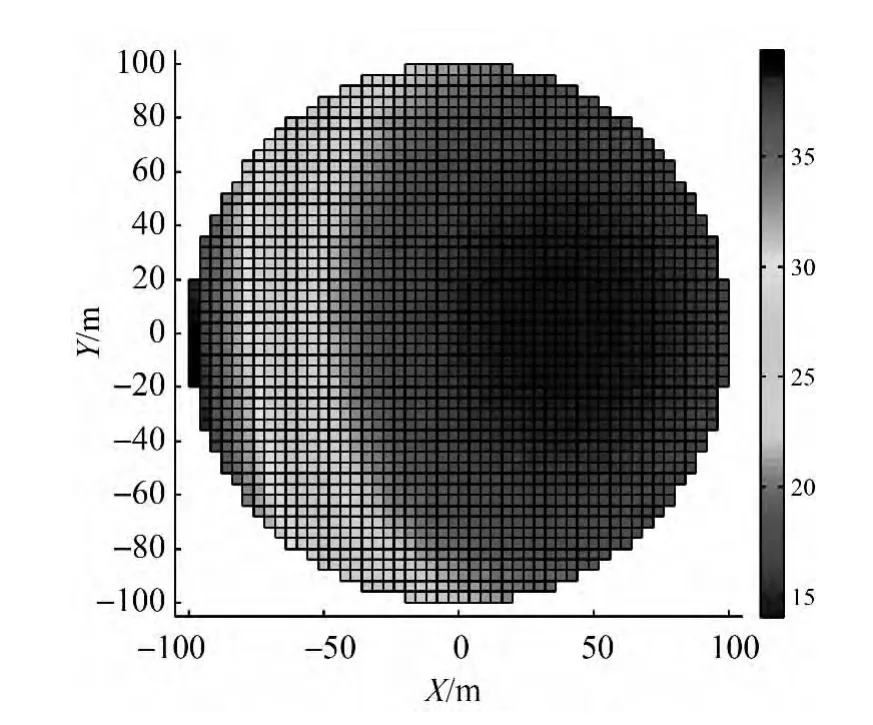
圖10 JD-21測站的高度角變化范圍

五、仿真測量定位精度分析

1.仿真測量方法

在JD-13、JD-14、JD-15、JD-17、JD-18、JD-19、JD-21、JD-22和JD-23共9個測站上設置9臺全站儀，采用極坐標法仿真測量下平臺9個棱鏡。由于饋源最大運動速度約為12 mm/s，全站儀在百米尺度上進行的是準靜態測量，距離和角度測量精度要低于標稱精度。仿真測量中，參考徠卡TCA1800全站儀測量指標，取距離動態測量精度2 mm+1×10-6D，水平角和垂直角動態測量精度4″［14］。觀測之前，全站儀需要進行定向，天文定向不失為一種有效的方法，即通過觀測恒星、行星或月球實現［15-16］。

下平臺的半徑按2 m計算，9個棱鏡均勻分布在圓周上。每臺全站儀跟蹤觀測固定的棱鏡，實時解算棱鏡在測量坐標系下的坐標。棱鏡在精調機構坐標系下的坐標可通過標較測量獲得，根據9個公共點的坐標，可以計算精調機構坐標系在測量坐標系下的位置和姿態，即實現饋源艙精調機構的位置和姿態測量。

2.仿真計算結果

圖11、圖12給出了9臺全站儀仿真測量精調機構的位置和姿態精度(RMS)。

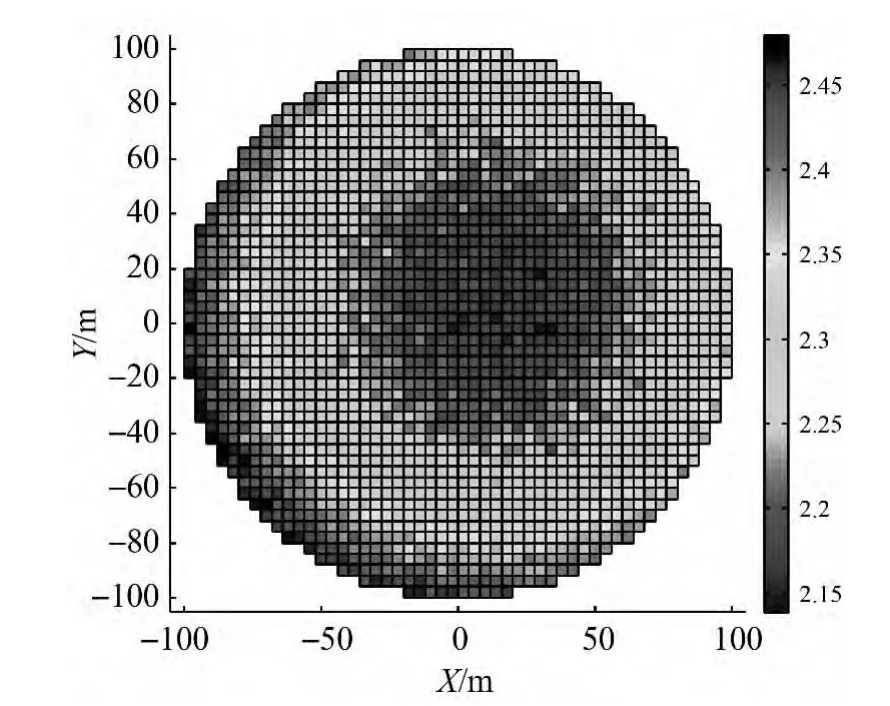
圖11 精調機構位置精度

由圖11、圖12可知，9個測站的定位精度優于2.5 mm，定姿精度優于360″，均達到精調機構對位置和姿態測量的要求。

3.系統可靠性分析

為了檢驗測量系統的可靠性，下面采用6個測站(JD-13、JD-15、JD-17、JD-19、JD-21、JD-23)跟蹤觀測6個棱鏡，仿真觀測條件不變，結果如圖13、圖14所示。

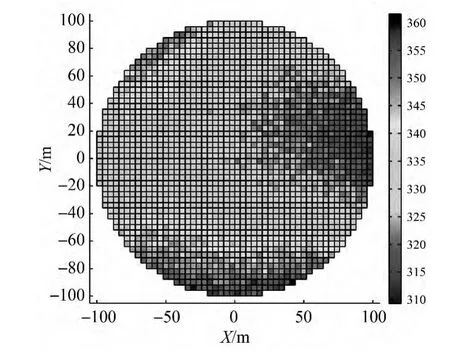
圖12 精調機構姿態精度

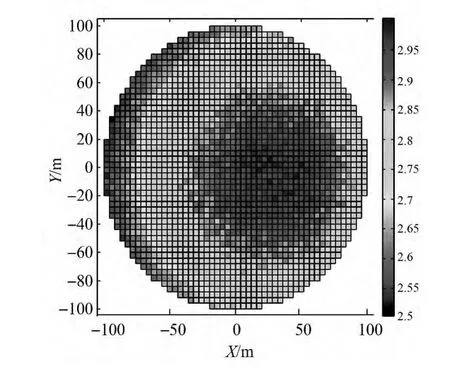
圖13 精調機構位置精度

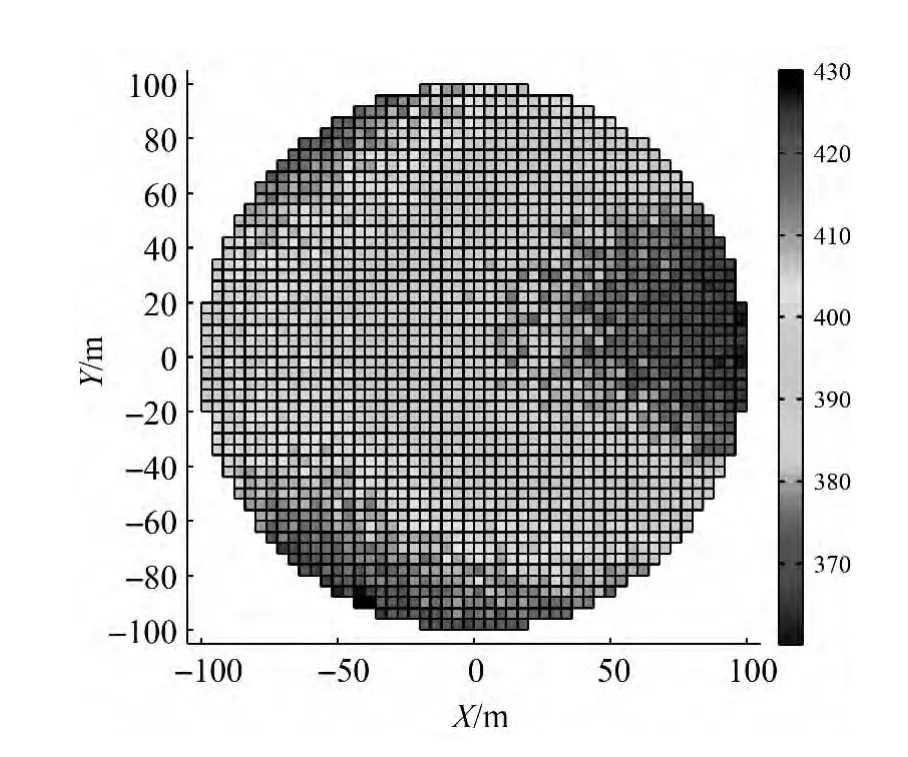
圖14 精調機構姿態精度

如圖13、圖14所示，6個測站的定位精度優于3 mm，定姿精度優于430″，均達到精調機構對位置和姿態測量的要求，說明測量系統在保證測量精度的同時，至少有3個測站可作為備份，系統具有較強的冗余性。

上述仿真計算沒有考慮實際測量中全站儀時間同步、測量時滯，以及風載荷等環境因素對測量精度的影響［17-18］。預計實際位置和姿態測量精度要低于仿真結果，系統的冗余測站數要少于3個。在具體的工程實踐中，可根據觀測經驗和效果，增減測站數目，節約測量成本。

六、結束語

本文對全站儀測量系統的測量條件進行了計算和分析，結果顯示，全站儀觀測棱鏡的最大入射角約為35°，平均值約為 13°～18°，由此產生的測量誤差可以忽略;觀測距離約為140～350 m;觀測高度角約為0～40°。仿真測量結果表明，9個測站的定位精度優于2.5 mm，定姿精度優于360″;6個測站的定位精度優于3 mm，定姿精度優于430″，均達到精調機構的位置和姿態測量精度要求。本文提出的基于全站儀的精調機構位置和姿態測量系統，具有良好的觀測條件和較高精度的定位定姿性能。

本文的研究論證了全站儀測量方案在FAST饋源艙精調機構位置和姿態測量中的可行性，對下一步的工程實踐具有借鑒意義。

［1］NAN R D.Five Hundred Meter Aperture Spherical Radio Telescope(FAST)［J］.Science in China Series G:Physics Mechanics and Astronomy，2006，49(2):129-148.

［2］朱麗春.500米口徑球面射電望遠鏡(FAST)測量與控制研究［D］.上海:中國科學院國家天文臺，2006.

［3］駱亞波.測量機器人在FAST饋源動態跟蹤測量中的應用［D］.鄭州:信息工程大學，2003.

［4］駱亞波，鄭勇，夏治國，等.測量機器人動態測量技術及應用研究［J］.測繪通報，2006(9):14-18.

［5］李明輝，朱麗春.FAST瞬時拋物面變形策略優化分析［J］.貴州大學學報:自然科學版，2012，29(6):24-29.

［6］路英杰.大射電望遠鏡饋源支撐系統定位與指向控制研究［D］.北京:清華大學，2007.

［7］KOVáCS E.Rotation about an Arbitrary Axis and Reflection through an Arbitrary Plane［J］.Annales Mathematicae et Informaticae，2012(40):175-186.

［8］何援軍.圖形變換的幾何化表示［J］.計算機輔助設計和圖形學學報，2005，17(4):723-728.

［9］王美山，李文亮，楊傳路，等.繞任意軸μ旋轉φ對應的歐拉角的新求解公式［J］.大學物理，25(9):31-33.

［10］王春艷，王志堅.基于旋轉矩陣理論的火炮定向精度分析［J］.光學精密工程，2004，12(4):108-111.

［11］劉萬里，歐陽健飛，曲興華.激光光束入射角度變化對角錐棱鏡測量精度的影響［J］.光學精密工程，2009，17(2):286-291.

［12］劉萬里，王占奎，曲興華，等.激光跟蹤測量系統跟蹤轉鏡的誤差分析［J］.光學精密工程，2008，16(4):585-590.

［13］武威.FAST主動反射面自動測量系統的研究［D］.鄭州:信息工程大學，2009.

［14］保宏，段寶巖，陳光達.具有慢速時滯機動目標三維跟蹤［J］.控制理論與應用，2006，23(4):526-530.

［15］詹銀虎，張超，鄭勇，等.月球視面中心擬合算法及其在測月快速定向中的應用［J］.測繪學報，2012，41(3):353-358.

［16］詹銀虎.基于自然天體的快速定向理論及技術研究［D］.鄭州:信息工程大學，2012.

［17］孫京海，朱文白，李輝.FAST大跨度索牽引運動控制系統全過程仿真分析［J］.高技術通訊，2012，22(2):192-197.

［18］GAWRONSKI W.Control and Pointing Challenges of Large Antennas and Telescopes［J］.IEEE Transactions on Control systerns Technology，2007，15(2):276-289.