跳馬落地速度與角度對落地穩定性影響的仿真研究

吳成亮，向家俊，徐 波，李旭鴻，肖曉飛，劉建宇，劉 錚，史東林

體操是我國的優勢項目，但從倫敦奧運會和近幾屆世錦賽成績來看，這個優勢在逐漸縮小，與世界強隊的差距正在擴大。體操落地技術是影響比賽成績的關鍵因素，它不同于其他項目（如跳高、跳遠）的落地動作，它要求落地站穩不動。國際體聯會（FIG）在2009年體操落地的評分規則［1］中規定：落地時腳移動一步將導致0.1～0.5的扣分；落地摔倒直接扣1分，而且還存在難度分認定不全風險。在當今的重大國際比賽中，運動員落地能否站穩不動，已成為能否奪冠和取得好成績的決定性因素之一。跳馬落地難度較大，也具有典型性；因此，研究跳馬落地穩定性是體育科學工作者們關注的熱點問題，并受到廣大教練員和運動員的重視。跳馬一般由8個動作階段組成，包括助跑、趨步、踺子、踺子踏跳、第一騰空、推馬、第二騰空和落地［2］。如今跳馬不斷地朝多軸的復合翻轉方向發展，這無疑加大了落地穩定性的難度。黃強等［3］對27屆奧運會我國男子體操選手落地穩定性進行統計與分析，結果表明落地動作完成較差，落地穩定的僅占43.19%。北京奧運會女子跳馬落地穩定性也不樂觀，在決賽16次試跳中，無一人能站穩，大部分選手落地會有一小步或中步移動，有4名運動員落地失敗。可見，跳馬落地穩定與否成為制約跳馬成績的關鍵因素。

目前，對跳馬落地穩定性影響的研究主要集中在跳馬落地技術與落地方式、肌肉組織的剛度和力量、心理調控能力等。嚴波濤等［4］對30人次的跳馬落地進行分析，建立跳馬落地的運動方程，指出落地的穩定性需要高質量的空中動作，旋翻轉體周數盡量提前完成，留有充足的空間和時間展體收臂準備著地。姚吉慶［5］對體操跳馬落地技術穩定性中分析指出：第2騰空階段技術好壞直接影響著落地技術的穩定性；良好的空間、時間知覺和訓練比賽中情緒變化也會影響到落地技術的穩定性。現有大多數研究是運用生物力學原理對落地穩定性進行定性分析，鮮有實驗數據作為支撐，且推理過程往往較為繁瑣；所以，本文在不考慮其他因素的前提下，旨在通過計算機建模與仿真技術，從速度和角度2個方面來分析跳馬落地的穩定性。

1 研究對象與方法

1.1 研究對象

程某，中國體操跳馬前世界冠軍，1988年出生，身高1.52 m，體重41kg。

洪某，朝鮮體操跳馬前奧運冠軍，1986年出生，身高1.54 m，體重42kg。

1.2 研究方法

1.2.1 三維運動學分析

對程某和洪某完成的“踺子轉體180°前手翻接直體前空翻轉體180°”跳馬動作，進行三維運動學分析。使用Troubleshooter高速攝像機拍攝，2臺攝像機同在跑道一側，夾角約70°，拍攝頻率為250幀／s。采用SIMI Motion軟件進行解析，獲得人體運動軌跡坐標、速度等運動學數據。

1.2.2 計算機仿真技術

基于MSC.ADAMS／LifeMod運動仿真軟件，輸入受試對象的性別、年齡、身高和體重等人體形態參數，根據人體模型數據庫GEBOD（Generator of Body Data）中的回歸方程計算得到環節長度、圍度和人體慣性參數等，建立19環節的人體模型，各環節之間由不同自由度的鉸鏈連接，共有52個自由度［6］。在此人體模型基礎上，對各環節的關節鉸鏈賦予約束，并調整人體模型的初始姿態，使它更接近實際的運動狀態；然后進行平衡分析，即將運動學解析得到的2人跳馬動作中人體各個關節的三維坐標賦予三維人體模型，其目的是使人體模型的關節中心和實際人體關節運動坐標點相匹配。再按GB／T 23124—2008建立跳馬的落地環境，即與人體相接觸的體操落地墊，并完成與人體模型的接觸。通過逆向動力學分析，記錄人體運動軌跡和各個關節力及力矩，再進行正向動力學分析，在關節力及力矩的驅動下，實現跳馬運動員落地過程中的人體運動仿真。最后將人在推離馬瞬間，身體重心的水平速度（vx）和垂直速度（vz）作為輸入條件變量，改變該變量值，以100%、105%及110%人體重心vx和vz組合輸入，進行仿真實驗，如圖1所示。

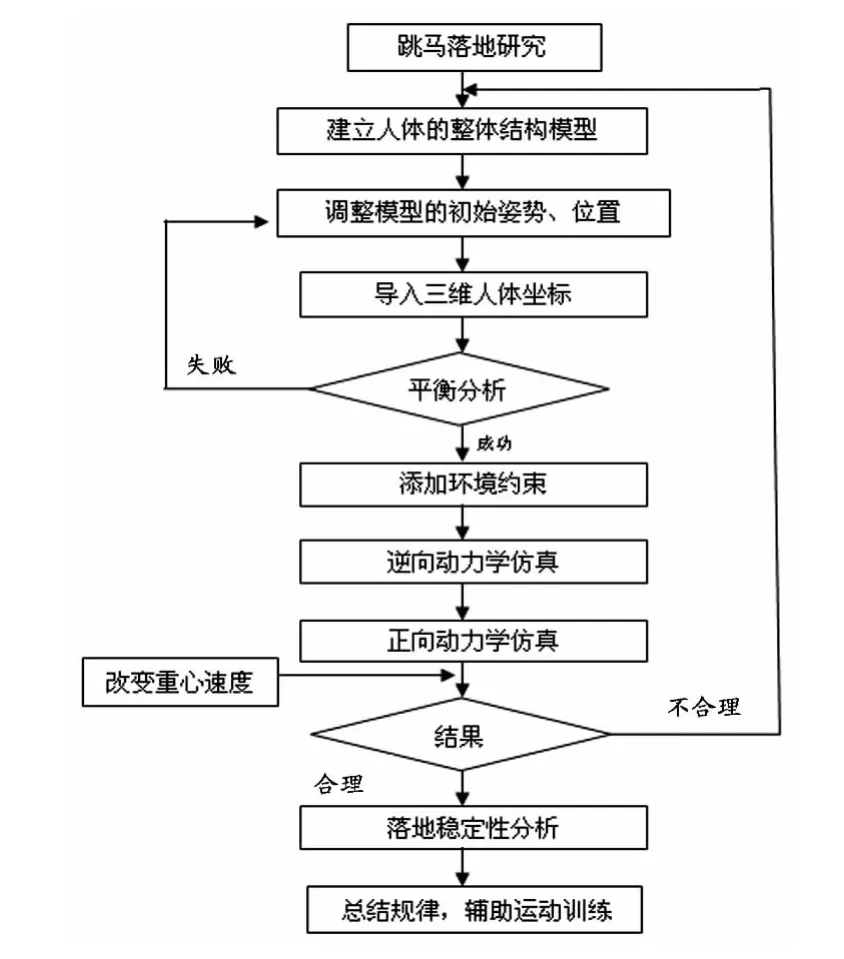
圖1 跳馬落地建模與仿真實驗流程

計算機仿真軟件MSC.ADAMS／LifeMod基于帶乘子的拉格朗日方程，并根據人體模型最終建立如下方程［8］：

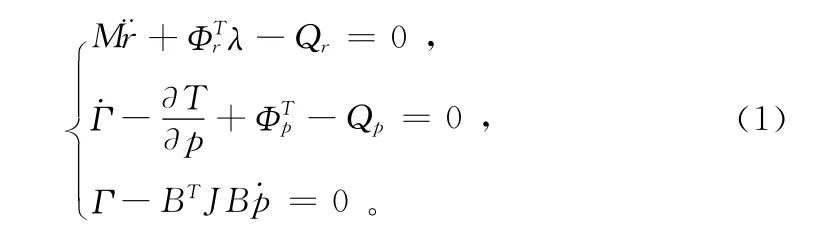
其中：M為廣義質量矩陣；Q為廣義外力矩陣；r、p為廣義位移矩陣；Γ為廣義角動量矩陣。最后需要輸出的仿真實驗結果是：落地瞬間人體的姿態角和人體重心的水平速度，如圖2所示。

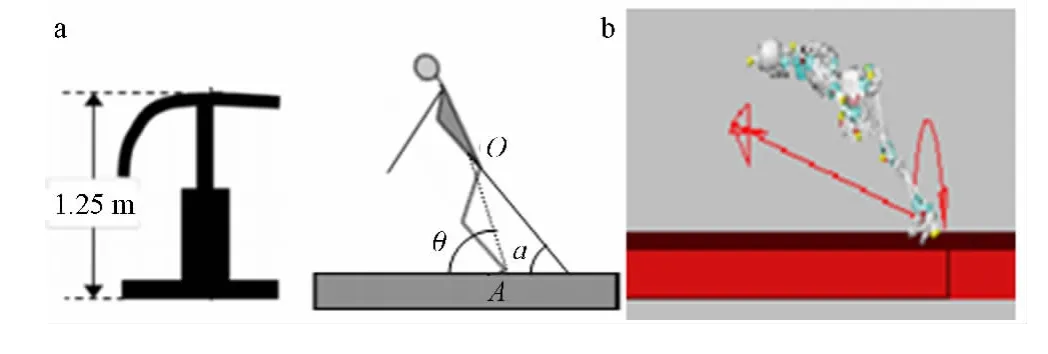
圖2 跳馬落地示意（a）和跳馬落地動作的計算機仿真（b）

2 結果

表1為在推離馬時將人體重心的水平速度vx和垂直速度vz作為變量輸入仿真模型，通過計算機仿真實驗后，得到落地瞬間人體的姿態角和人體重心的水平速度。從表1可以看出，當只增加推離馬的水平速度vx時，落地時的水平速度也相應增加，但是人體落地姿態角是先增加后下降的。當只增加推離馬的垂直速度vz時，落地時的水平速度沒有增加，人體落地姿態角變化暫不顯示規律性。當推離馬的水平速度vx和垂直速度vz同時增加時，落地時的水平速度和人體落地姿態角都相應增加了。

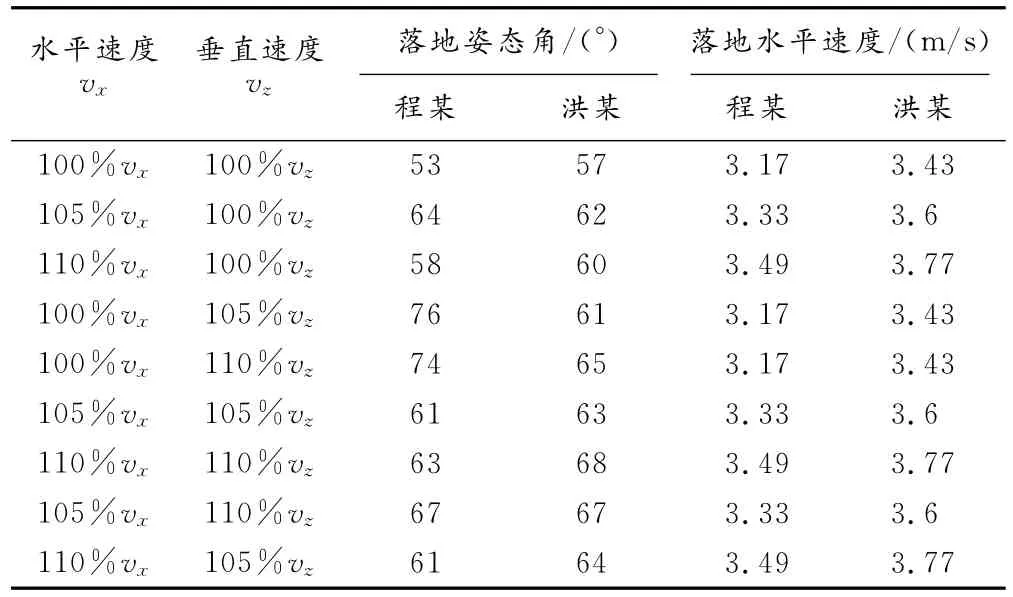
表1 程某、洪某在推離馬時不同水平速度和垂直速度下，落地瞬間身體姿態角和水平速度

如圖3所示，僅改變程某推離馬時身體重心垂直速度，左圖的實線表示該動作的實際速度（2.64m／s，高速攝影解析得到的速度在這里稱為實際速度），虛線“－－”表示105%實際速度（2.80m／s），隔 點 虛 線 “－·－”表 示 110% 的 實 際 速 度 （2.94 m／s）。右圖黑色方塊和斜線方塊分別代表在這3種重心垂直速度下第2騰空所用時間和人體重心水平位移，3條曲線可以明顯地看到程某第2騰空階段盆骨中心的高度隨時間的變化情況，身體重心垂直速度越大，人體盆骨中心越高；從柱形圖來看，身體重心垂直速度的增加，也帶來人體的水平位移和第2騰空所用時間的增加。

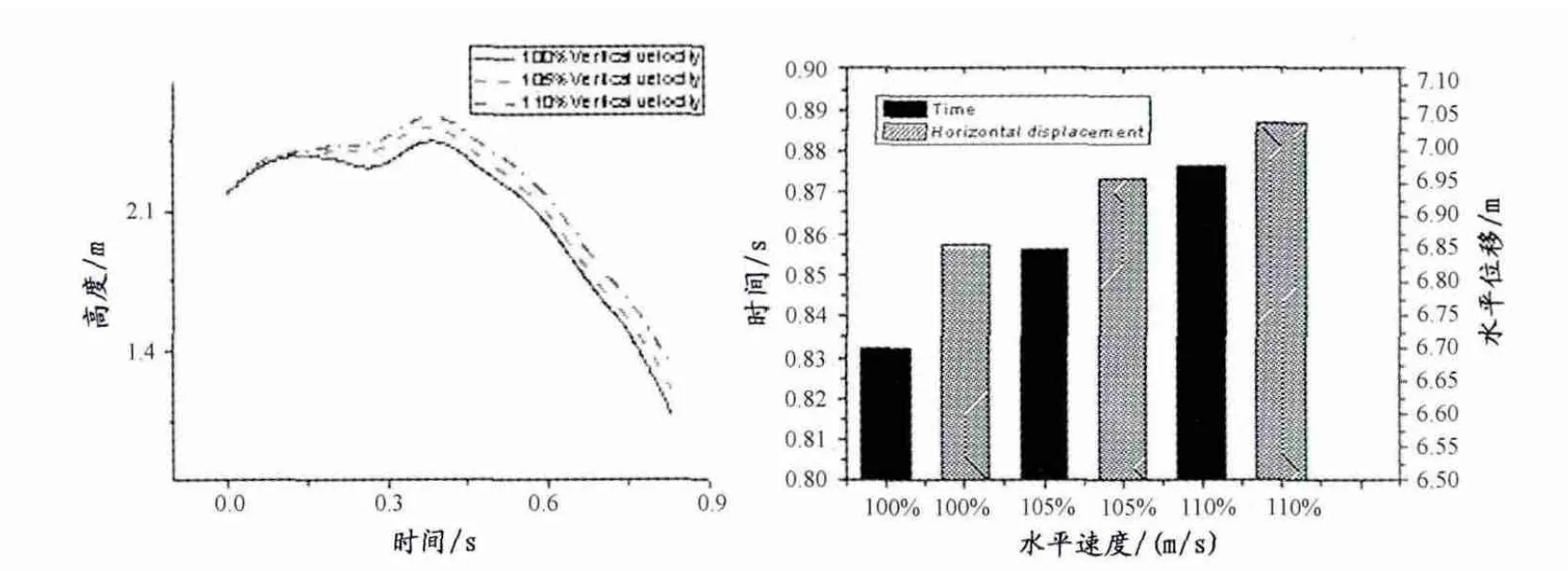
圖3 程某推離馬時重心不同垂直速度，人體盆骨中心高度－時間變化曲線（左），身體水平位移及第二騰空時間（右）

如圖4所示，僅改變程某推離馬時身體重心水平速度，左圖實線表示該動作的實際速度（3.17m／s），虛線表示105%的實際速度（3.33m／s）。右圖黑色方塊和斜線方塊分別代表在這2種重心水平速度下第2騰空所用時間和人體重心水平位移。從曲線圖可以看到，2條實線和虛線完全重合，看起來只有1條曲線；所以，身體重心水平速度的改變，對于骨盆中心高度沒有變化。從柱形圖上看，當身體重心水平速度增加了，人體的水平位移也會增加，但第2騰空所用時間沒有增加。圖5為程某（左）和洪某（右）跳馬第2騰空及落地動作仿真圖。

據統計，2013年，湖南累計投入抗旱資金24.2億元，抗旱機電井25.5萬眼、抗旱泵站3.86萬處、機動抗旱設備83.8萬套、運水車輛1.75萬輛，完成抗旱灌溉面積1958萬畝，挽回糧食損失300多萬t，減少經濟作物損失60億元，臨時解決了314萬人的飲水困難，有效保障了群眾生活和農業生產安全。

3 分析與討論

體操技術發展迅速，跳馬空中動作越來越驚險、復雜，它既要表現出“高飄”，又要表現出舒展大方，最后落地要穩定，給人以美的享受。跳馬落地瞬間，通常是決定成敗的關鍵。隨著跳馬難度增加，落地的穩定性相對下降，如果不注意落地中的技術問題，還容易造成關節損傷，尤其是膝、踝關節［9］。人體運動的計算機仿真是運動生物力學理論方法中較高層次的研究內容［10］，它可以實現人體運動的計算機仿真實驗及結果的可視化［11］，為揭示運動技術特點提供直觀的素材，為教練員指導跳馬訓練提供科學的理論依據。

3.1 跳馬落地技術分析

落地技術是指跳馬動作技術環節中，從腳接觸體操落地墊，再經過緩沖到身體起立站穩階段的技術［12］。落地技術穩定性實際上是指運動員根據不同的下法動作充分調整身體姿勢，抵消傾倒力矩能力的穩定性。落地技術它包括相互聯系的2個階段：準備階段、落地緩沖階段。

準備階段中，人體在空中完成各種動作難度后，兩腳在還未觸墊前，身體處于準備落地姿態。這一階段對落地的穩定性有直接影響，跳馬第2騰空動作一般以繞人體橫軸較多。根據轉動慣量原理：I＝mR2（其中m為人體的質量，R為人體的回轉半徑）。m不變，I與R2成正比，即R增大到原來的2倍，I就增大到原來的4倍。此外，I與角速度ω成反比（人在騰空之后，只受重力作用，根據動量矩守恒：Iω＝常量），所以當R增大時，I隨增大，而ω減小，即當人體轉動的半徑增大時，其轉動速度相應減小。因此，在人體完成空翻動作后，身體要做一定的伸展，以減小落地時的角速度，增加落地的穩定性。另外，這樣做同時增加肌肉的初長度，使落地時肌肉發揮更大的力量，有助于落地站穩。

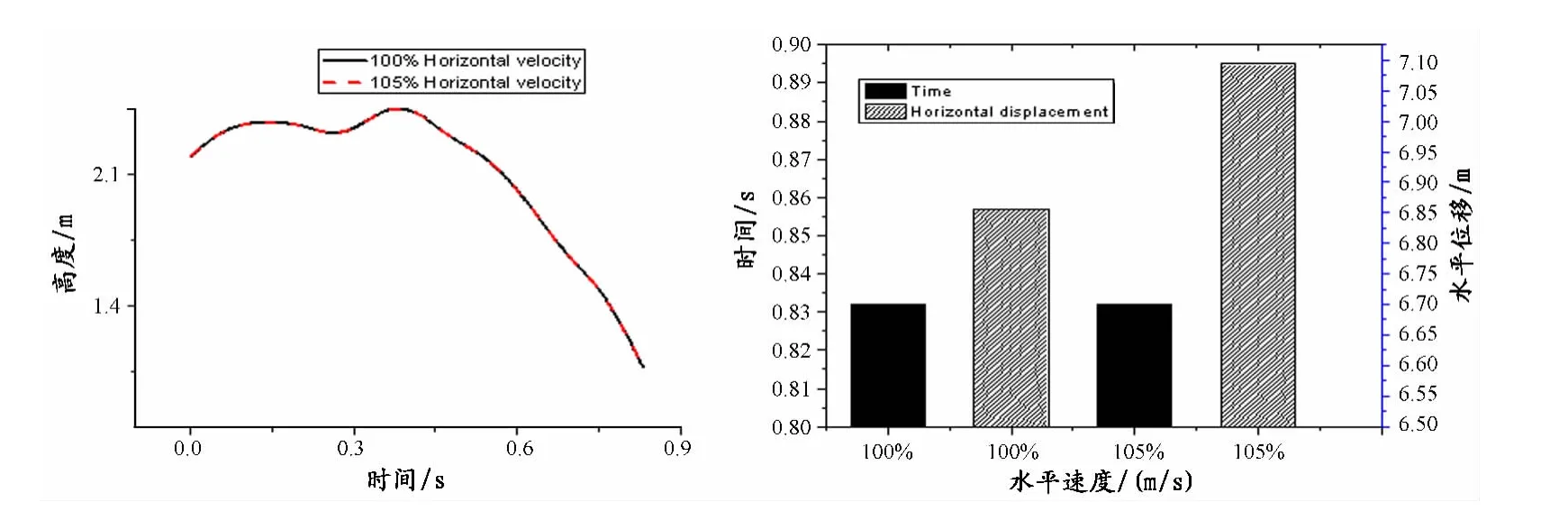
圖4 程某推離馬時重心不同水平速度，人體盆骨中心高度－時間變化曲線（左），身體水平位移及第二騰空時間（右）

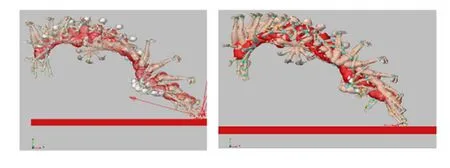
圖5 程某（左），洪某（右）跳馬第二騰空及落地仿真

落地緩沖階段，此階段又包括一個較短的沖擊階段和一個較長的平衡穩定階段［13］。在沖擊階段，腳－落地墊間存在較大的地面反作用力（GRF），其峰值隨著推離馬高度（第2騰空高度）增加而增大，大約是運動員自身體重的8～14倍，而在較長的平衡穩定階段，GRF大致為其體重［14］。落地緩沖技術是穩定的關鍵，其生物力學特點是落地瞬間的水平分力及翻轉力矩，通過合理緩沖使之消失，垂直分力逐漸趨近體重，即人體所受的合外力、合外力矩為零。在緩沖制動過程中，動力矩M主動必須始終大于破壞平衡的傾倒力矩M傾倒。當制動結束時M主動＝M傾倒，此時人體站立不動；所以人體受到的合外力、合外力矩為零，是站穩不動的必要和充分的條件。沖擊階段雙腿肌肉用力特點是由積極主動的退讓性工作過渡到克制性工作；落地方式由腳尖落地過渡到全腳掌，原因在于足尖落地時足弓等部位較好的變形和緩沖、踝關節處肌肉的預激活等大大降低了腳跟的負荷。雙臂需要適度擺動，以保持平衡。

3.2 跳馬計算機仿真模型的落地速度及角度分析

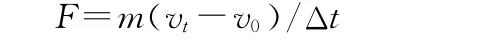
其中F為沖力（即地面給人體作用力的合力），m為人體質量，vt為瞬時末速度，v0為瞬時初速度，Δt為人體接觸地面緩沖時間。人體質量m一般短時間內不會改變，人體接觸地面緩沖時間Δt越長，F會越小，落地會越穩定；但Δt與落地高度、動作控制、下肢神經肌內的控制和協調能力、肌肉組織的剛度和力量、落地方式和落地墊的力學特性等因素都有關［18］，相互關系較為復雜，不做詳細討論。本文假定Δt不變，只探討落地的速度和角度對跳馬落地穩定性的影響。落地瞬時末速度vt一般為零，所以當落地瞬時初速度v0越大時，F越大，人要落地站穩越難。落地垂直速度是由落地高度決定的，落地高度越高，第2騰空的時間越長，運動員有足夠的時間完成翻騰和／或轉體動作，這就越有利于跳馬動作的完成；所以不應該以犧牲落地垂直速度為代價，影響落地高度。因此，減小落地時的水平速度，是增加落地穩定性的很好選擇，但是過小的水平速度，可能引起落地階段的遠度不足，造成完成分（E分）被扣［1］。所以，在跳馬的計算機仿真實驗中，為了不影響落地穩定性，在不減小落地水平速度的情況下，應增加推離馬的垂直速度，來增加第2騰空高度，這有利于跳馬動作的完成。

本研究通過計算機仿真實驗，只增加推離馬的垂直速度，對于落地姿態角影響不大，在53°～76°內呈不規則變化（見表1）。只增加推離馬的水平速度時，落地姿態角先增加后減小，姿態角的減小是為了降低水平速度的增加對落地穩定性的影響。設人體落地時主矢和主矩不為零，主矢量與地面有夾角為α（如圖2所示），則相對A點產生動量矩MA，其大小MA＝mvrsin（θ－α）（順時針方向），其中v為O點瞬間線速度（以A為支點，OA為半徑r的轉動）；重力相對A點產生重力矩M重＝mgrcosθ（逆時針方向）。當MA＝M重，人體落地站立不動，這是理想結果。當MA＞M重或MA＜M重時，則人體前倒或后倒。

若MA＝M重，即mvrsin（θ－α）＝mgrcosθ，那么 在不考慮跳馬落地失敗的情況下，由表1可知，人體落地姿態角θ范圍在53°～76°，為銳角，又因為α≤θ，則

假設當角α＝0，即v正好等于人體落地水平速度，則

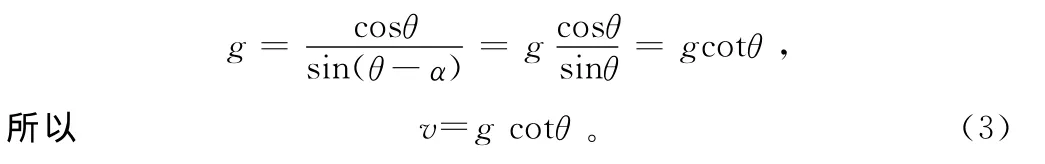
假設當α＝90°，v為人體落地垂直速度，此時落地無水平速度，落地的穩定性更多與人體落地緩沖能力有關。

通常情況下，運動員跳馬落地是既有水平速度又有垂直速度。人體垂直速度給落地帶來的不穩定因素更多與運動員的緩沖能力有關，本文不做討論。而對于跳馬中人體落地水平速度與落地姿態角應更多地考慮v＝gcotθ的函數關系，通過計算機仿真獲知，人體落地姿態角θ范圍在53°～76°，函數在該區間為減函數；所以，人體水平速度與落地姿態角應該呈負相關，即當水平速度增加時，落地姿態角必須減小才能滿足落地的穩定性。但是落地姿態角減少，將使人在落地時控制平衡的難度增大，使落地穩定的風險增加。當推離馬的水平速度和垂直速度同時增加時，落地姿態角和水平速度都會增加，MA將進一步增加，人體向后傾倒趨勢增加，造成落地穩定的難度更大。

本文還對計算機仿真實驗結果，進行了理論驗證。根據拋物線運動原理，跳馬第2騰空到落地過程，屬于落地點在拋出點下的拋物線運動。設v0為推離馬瞬間身體重心速度，φ為v0與水平夾角，則有，推離馬瞬間身體重心水平速度vx＝v0cosφ，垂直速度vz＝v0sinφ。

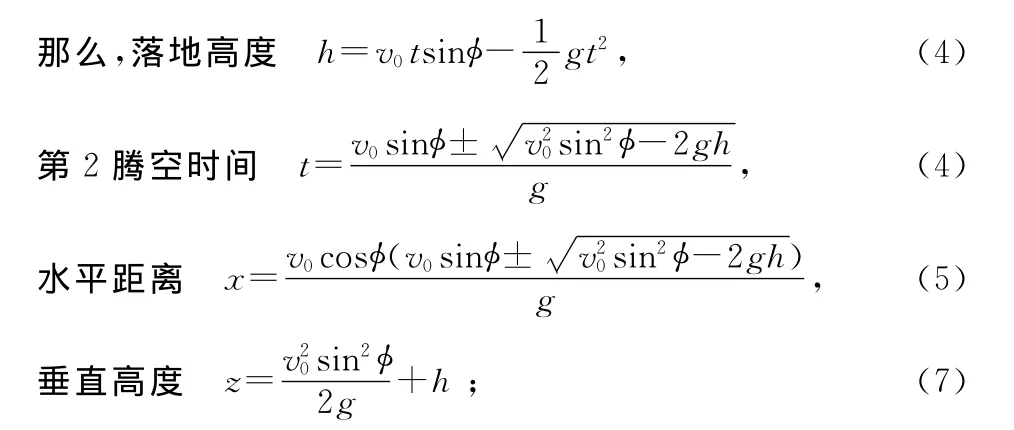
所以，式（5）和（6）式分別說明在拋物線運動中，物體飛行時間和高度由初速度的垂直分量決定，而不受初速度水平分量的影響（不計空氣阻力）。如圖3所示，身體重心的垂直速度增加了，第2騰空高度和所用時間都會增加，有更多的時間和空間完成第2騰空動作，提高伸展身體，增加落地的穩定性。而在圖4中，只改變了身體重心的水平速度，垂直速度沒有改變，所以第2騰空高度和所用時間都沒有發生改變，而落地的水平距離增加，這樣就增加了落地穩定的難度。以上采用計算機仿真實驗所得出的仿真結果，與拋物線運動原理相吻合，這就從拋物線運動原理對本研究中計算機仿真實驗結果進行了理論驗證。

4 結論

本文利用高速攝影這一運動生物力學較為成熟的技術手段，獲得人體運動三維坐標，再基于MSC.ADAMS／LifeMod多體動力學仿真軟件，對跳馬落地進行仿真實驗。以跳馬推離馬時的水平速度和垂直速度作為變量，獲得不同條件下的落地水平速度和落地姿態角，并分析它們對落地穩定性的影響。結果表明：在跳馬落地的最佳策略為，在保持推離馬時人體重心水平速度不減小的情況下，增加其垂直速度，能產生更多的時間和空間完成第2騰空動作，并為落地作積極準備；而在即將落地前，身體要做一定的伸展，以減小落地時的角速度，增大落地時的轉動慣量，從而增加落地的穩定性。

誠然，本研究僅從落地速度和角度來評判落地穩定性，不可避免地存在一些局限性。本文將人體簡化為多剛體模型，忽略了肌肉和軟組織對運動的影響，本身會帶來一定誤差。盡管如此，但我們可以通過模型評估出很難在人體上測量的結果，從而確定最佳的運動模式。今后的研究方向需要將模型的效度不斷提高，將肌肉和軟組織引入。綜上所述，計算機仿真技術也必將在運動訓練指導及運動損傷預防上擁有廣泛的應用前景。

［1］國際體操聯合會.女子競技體操評分規則［S］.2006.

［2］郝衛亞，姚俠文，龐樂.程菲跳運動學分析［J］.中國體育科技，2007，43（6）：76－79.

［3］黃強，蔣小娟.對第27屆悉尼奧運會我國男子體操選手落地穩定性的統計與分析［J］.福建體育科技，2001，20（3）：16－19.

［4］嚴波濤，于長菊，張伯強.體操跳躍類動作落地穩定性的生物力學原理探討［J］.西安體育學院學報，1994.11（2）：64－71.

［5］姚吉慶.論競技體操跳馬落地技術穩定性［J］.武漢體育學院學報，2003，37（3）：74－76.

［6］吳成亮，郝衛亞.跳馬過程中人－器械動力學關系的研究［J］.中國體育科技，2011，47（6）：25－29.

［7］GB／T23124－2008.中華人民共和國國家標準跳躍平臺［S］.2008.

［8］劉雷.人體運動仿真建模方法研究［J］.計算機仿真，2009（1）：166－168.

［9］弗拉基米爾M·扎齊奧爾斯基.運動生物力學［M］.北京：人民體育出版社，2004：531－554.

［10］盧德明.運動生物力學測試方法［M］.北京：北京體育大學出版社，2001：222－226.

［11］郝衛亞.人體運動的生物力學建模與計算機仿真進展［J］.醫用生物力學，2011，26（4）：97－103.

［12］李旭鴻，郝衛亞.落地沖擊引起下肢損傷的生物力學研究進展［J］.中國運動醫學雜志，2013，32（2）：186－189.

［13］McNitt－Gray J L.Kinematics and impulse characteristics of drop landings from three heights［J］.Int J Sport Biomech，1991，7（9）：201－224.

［14］McNitt－Gray J L，Hester D M E，Mathiyakom W，et al.Mechanical demand and multijoint control during danding depend on orientation of the body segments relative to the reaction force［J］.J Biomech，2001，34（11）：1471－1482.