基于教材感悟思想導向思維
——一道源于教材的中考試題命題的實踐與思考

●傅瑞琦(金華市教育局教研室浙江金華321000)

基于教材感悟思想導向思維
——一道源于教材的中考試題命題的實踐與思考

●傅瑞琦(金華市教育局教研室浙江金華321000)

試題設計一直重視教材資源的應用和拓展，特別是試卷中的關鍵試題.由于承擔著考查學生探究能力、實踐能力和創新能力等數學素養的重任，更需要立足教材，依據教材素材，改編形成試題，力求在學習經驗積累、問題解決能力以及數學潛能上對學生適度區分，達到對“數學深層思維”的考查目的.現以2014年數學中考金華卷第24題的命制過程，淺談如何利用教材資源，探討壓軸題編制的嘗試與完善.

1 教材素材

根據命題計劃，最后一題的素材選自教材.我們期望，一是背景設計為學生熟悉;二是考查內容選自數學核心知識的交匯處;三是改編為具有開放性、動態探究相結合的綜合性問題，將觀察、探究和計算有機融合，綜合考查學生靈活應用所學知識和經驗去分析問題、解決問題的能力.

素材已知:如圖1，P是∠AOB內一點，PD⊥OA，PE⊥OB，D，E分別是垂足，且PD=PE.求證:點P在∠AOB的平分線上.

圖1

素材解讀這是浙教版八年級上冊2.8節“直角三角形全等的判定”中的范例，通過應用直角三角形全等的判定方法，得出角平分線性質定理的逆定理.若聯結DE，則△PDE是等腰三角形.

改∠AOB為鈍角，點P是一動點，研究△PDE是等腰三角形的存在性問題.

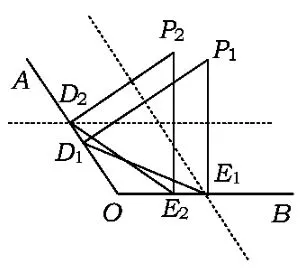
圖2

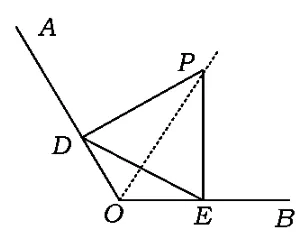
圖3

圖4

1)若△PDE是等腰三角形，點P的位置除了在∠AOB平分線上外，還有2種情況(如圖2):當DP=DE時，點D在線段PE的中垂線上;當EP= ED時，點E在線段PD的中垂線上.

2)若∠AOB=120°(如圖3)，則△PDE是正三角形.

3)若∠AOB=135°，除了∠AOB的角平分線上的點P外(如圖4)，還存在△PDE是等腰直角三角形2種情況.

結合上面的分析，將背景放置在直角坐標系中，對點P的位置給出一定的限定，尋找隱含在其中的幾何基本圖形，讓學生對等腰三角形的存在性問題進行探究，形成初稿分析考查的可行性.

2 研究過程

初稿在平面直角坐標系中，直線l:y=-x-4與x軸交于點E，過拋物線上的點P分別作x軸、直線l的垂線，垂足為E，F，當△PEF為等腰三角形時，試求點P的橫坐標.

分析設點P的橫坐標為t.如圖5，△PEF是等腰直角三角形，有t1=-4;如圖6，△PEF是等腰直角三角形，與x軸成45°角的直線PF與拋物線的交點有P2和P3這2種情況，直線PF的解析式為y=x+4，由，解得

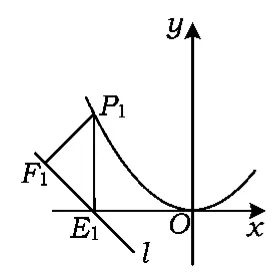
圖5

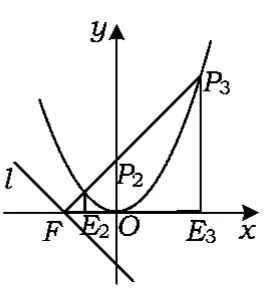
圖6

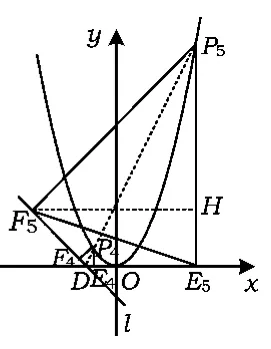
圖7

如圖7，點P在∠ODF的角平分線上，過點F作FH⊥PE，由，得方程

但該方程的一次項系數、常數項都含有根式，求解已經超出課標要求.

調整直線l的位置，并將拋物線改為雙曲線形成第2稿.

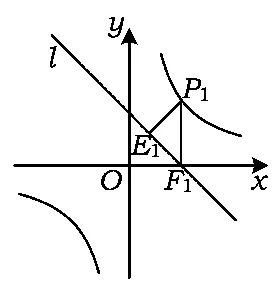
圖8

圖9

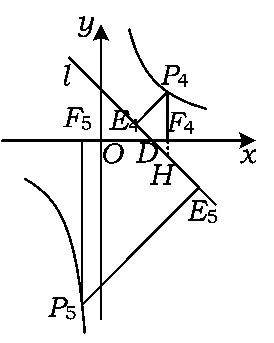
圖10

分析如圖8，△PEF是等腰直角三角形，可以求得點P1的橫坐標為.如圖9，△PEF是等腰直角三角形有2種情況，設P1F2=F2E=t，則

如圖10，點P在角平分線上，延長P4F4，交直線l于點H，設DF4=DE4=t，則

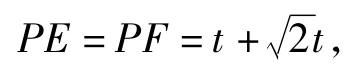
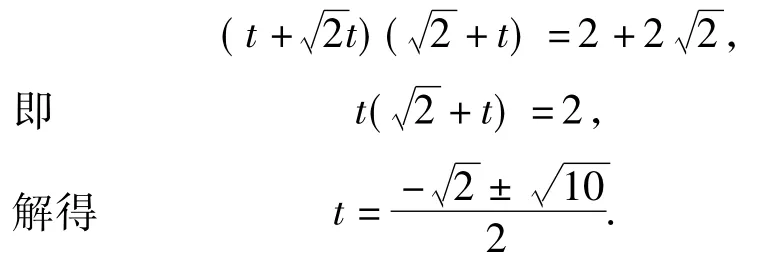
另外，從圖形看，點P的位置是直線l與x軸夾角平分線與拋物線或雙曲線的交點，求2個圖像的交點坐標即為點P的坐標，計算復雜，方法單一.

因此，基于選擇拋物線、雙曲線都會出現超標的方程，因此改為直線型圖形就可以避免這種情況，于是形成第3稿(定稿).

3 定稿分析

定稿如圖11，直角梯形ABCO的2條邊OA，OC在坐標軸的正半軸上，BC∥x軸，OA=OC=4，以直線x=1為對稱軸的拋物線過點A，B，C.

1)求該拋物線的函數解析式.

2)已知直線l的解析式為y=x+m，它與x軸交于點G，在梯形ABCO的一邊上取點P.

①當m=0時，如圖11，點P是拋物線對稱軸與BC的交點，過點P作PH⊥直線l于點H，聯結OP，試求△OPH的面積.

②當m=-3時，過點P分別作x軸、直線l的垂線，垂足為點E，F.是否存在這樣的點P，使以P，E，F為頂點的三角形是等腰三角形?若存在，求出點P的坐標;若不存在，請說明理由.

圖11

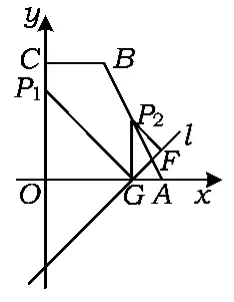
圖12

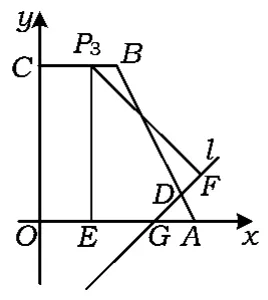
圖13

圖14

分析第①小題應盡可能讓學生得分，入口要寬，設置的問題“當m=0時，求△OPH的面積”.一方面，當m=0時，直線l過原點，使問題背景更簡潔，在對問題的理解上作了鋪墊;另一方面，求△OPH的面積時，需要用到PH與拋物線對稱軸夾角45°這一結論，這為第②題的求解起到引領思路的作用，從而降低求解難度.

第②題的求解，對2種等腰直角三角形的2種情況(如圖15)，只要能夠分析畫出圖形，求出點P的坐標，是容易的.對后2種的求解則需要有一定的綜合分析能力.

如圖13，點P在邊BC上，則點P為∠OGD的角平分線與BC的交點，有GE=GF，設為t.

方法1如圖15，過點F分別作FH⊥PE于點H，FK⊥x軸于點K，則△PHF，△FGK為等腰直角三角形，從而

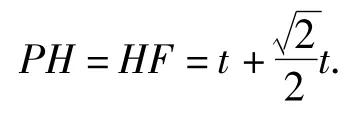
由PE=PH+EH，得

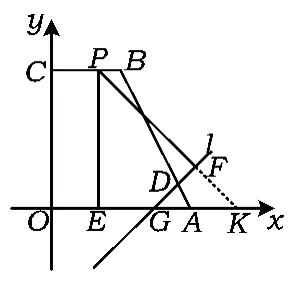
圖16

圖17

方法4如圖18，過點F構造矩形PQKE，則

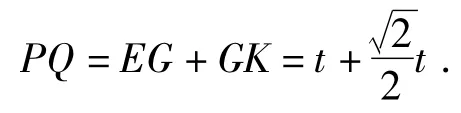
由QF=PQ，得

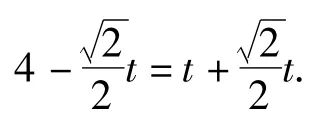
圖18

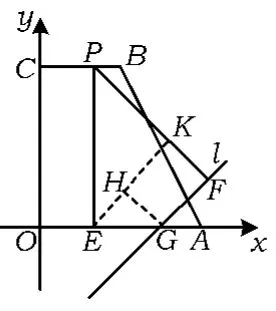
圖19

圖20

方法5如圖19，分別過點E，G作直線l，PF的平行線，相交于點H，則

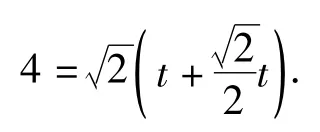
方法6如圖19，過點E作EK⊥PF于點K，GH⊥EK于點H，則

方法7如圖20，延長FP交y軸于點K，設CP=m，則△KFH是等腰直角三角形.由，得

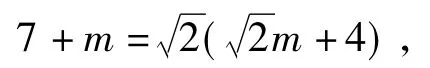
方法8如圖21，延長CP交直線l于點K，設CP=m，則△KCH，△PFK是等腰直角三角形.由CH=CK，得

圖21

4 命題反思

4.1 選擇教材素材，引導教學導向

教材是課程標準的載體，是課程目標和課程內容的具體化，以教材中的核心概念、性質法則和例題習題為載體，將有效地檢測學生對知識的理解與掌握程度，而背景“親切熟悉”，可以確保情境的公平性，將有利于學生的發揮.選擇一個核心的教材內容，加工改造，將解決問題需要的數學思想方法和數學文化內隱其中，就可以創造出一個嶄新的試題.

角平分線定理、等腰三角形等問題都是學生熟悉的，頂點P在梯形邊上運動，很自然地將角平分線定理的基本圖形內隱其中，但夾角為45°角的不變性，為圖形的分析給出思路和求解方向.既保證了情境的公平性，尊重了學生認知水平的差異，又對引導課堂教學回歸教材，師生重視教材、用好教材，對減輕學生課業負擔、減少題海戰術有一定的現實意義，對教學有著積極的導向作用.

4.2 問題引導探究，感悟數學思想

依托課本素材進行命題，反應數學的本質.本題是等腰三角形存在性探究問題，難于用兩點距離公式進行求解，引導學生畫出圖形，根據圖形的特征尋求解題思路.

問題的設置，基于對學生知識水平和活動經驗積累的了解;問題的呈現，采用遞進式的循序漸進.第1)小題入口窄，對最后一問的求解提供思路或知識的鋪墊;第2)小題的解決，對等腰直角三角形2種情況，求解通過畫圖是不難發現其結果的，但角平分線上2個點的求解，涉及不同的數學思想方法，增加圖形分析的轉化層次，增加題目分析過程的復雜性，需要學生較高的思維能力，比較豐富的數學積累，來表現出自己在從事觀察、數學表達、猜想、推理等數學活動方面的能力，在問題的探究解決過程中，能很好地甄別學生的數學素養.

4.3 解題思路多元，突出考查思維

試題的設計應突出數學思想方法的應用價值，增加思維量而適當控制計算量.如圖13，當點P為直線l與x軸夾角的角平分線與梯形的邊的交點時，圖16～19所示的方法都是根據“∠EPF=45°”這一圖形特征，用不同的形式補成等腰直角三角形.圖18中補成一個矩形，出現2個等腰直角三角形;圖19中則分割成1個矩形和2個等腰直角三角形;而圖15中則補成直角梯形，再利用直角梯形的特征分割成矩形和一個等腰直角三角形.通過割補這2種常見手段，出現等腰直角三角形，轉化為方程問題得到解決.