基于誤差四元數的單兵導航系統算法*

于 飛，白紅美，葉 攀，高 偉，，趙 博

(1.哈爾濱工程大學自動化學院，黑龍江哈爾濱150001;2.哈爾濱工業大學鞍山研究院，遼寧 鞍山114000)

0 引言

單兵導航系統的一大難題在于如何獲得準確的航向信息，為解決航向估計問題，減小單兵定位誤差，文獻［1］利用地圖匹配輔助微型慣性測量單元(MIMU)的算法對單兵進行定位。此算法需針對已知環境，且計算量較大。文獻［2］采用啟發式偏移消除算法對單兵姿態進行修正，但要求單兵處于直行運動狀態。

在磁干擾較弱的環境，考慮到MEMS陀螺和磁力計互補的性質，本文提出基于誤差四元數的多傳感器信息融合算法。通過磁力計標定技術補償外界磁干擾，并以MEMS加速度計和磁力計輸出為姿態基準，利用卡爾曼濾波器對誤差四元數和陀螺漂移進行估計，以減小單兵定位誤差。

1 磁力計標定

每次使用前利用標定實驗對磁力計進行標定可有效補償外界磁干擾的影響［3］。標定前后的磁場強度如圖1。

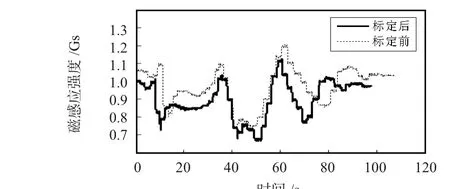
圖1 標定前后的磁場強度Fig 1 Magnetic field intensity before and after calibration

由圖1可以看出，標定前后的磁力計輸出存在明顯差距，通過標定能夠有效補償外界磁場的影響。

2 多傳感器數據融合算法

基于誤差四元數的數據融合算法流程圖如圖2。

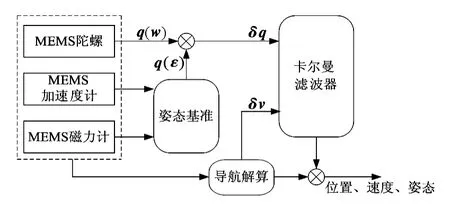
圖2 數據融合算法流程圖Fig 2 Flow chart of data fusion algorithm

首先利用MEMS陀螺獲得更新四元數，磁力計和加速度計獲得姿態基準;然后以誤差四元數和速度誤差為觀測量實現濾波更新;最后利用估計結果修正導航參數，得到修正后輸出。

2.1 狀態模型分析

以誤差四元數和陀螺漂移為狀態向量

其中，δqi(i=1，2，3，4)為四元數元素，εj(j=x，y，z)為陀螺漂移。

非線性系統模型為

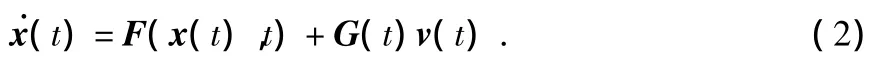
其中，F為狀態轉移矩陣，G為噪聲驅動矩陣，v為系統噪聲。

定義誤差向量δx為

其中，x(t)為濾波估計值，xr(t)為向量的真實值。在真值處進行一階泰勒展開［4］，可得到關于誤差向量的模型為

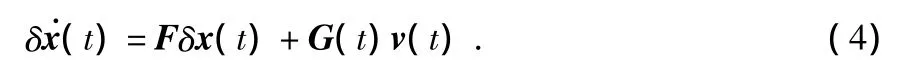
四元數微分方程為

由式(4)和式(5)得到誤差四元數的微分方程

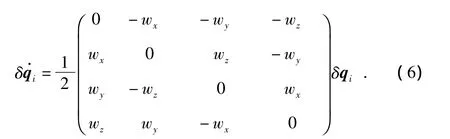
對陀螺漂移進行一階高斯馬爾科夫建模

其中，εj為陀螺漂移，βj為相關時間的倒數，σ2j為陀螺信號的協方差，v為零均值高斯白噪聲。

由式(6)和式(7)得到系統狀態模型

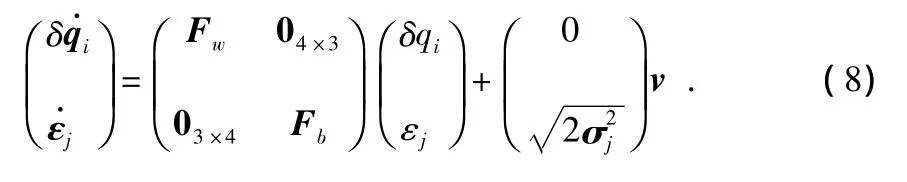
其中，Fw和Fb分別為與w和βj相關的矩陣

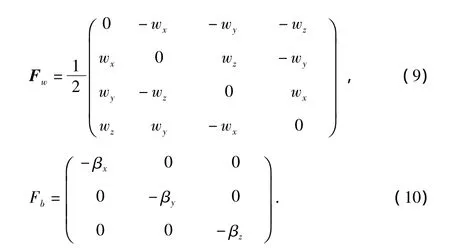
2.2 量測模型分析

量測更新過程由MEMS加速度計、陀螺和磁力計共同完成。姿態基準測量由MEMS加速度計、磁力計獲得。陀螺主要用于濾波更新階段。由陀螺輸出可得到旋轉四元數［5］q(w)

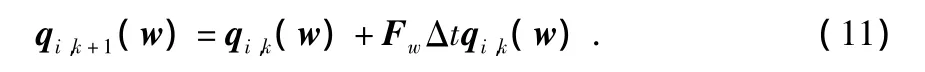
其中，k為某一時刻，Δt為采樣間隔。

在磁干擾較弱的地方，可由標定后的磁力計輸出得到航向值［6］。將載體系的磁力計測量值Bbk投影到導航系

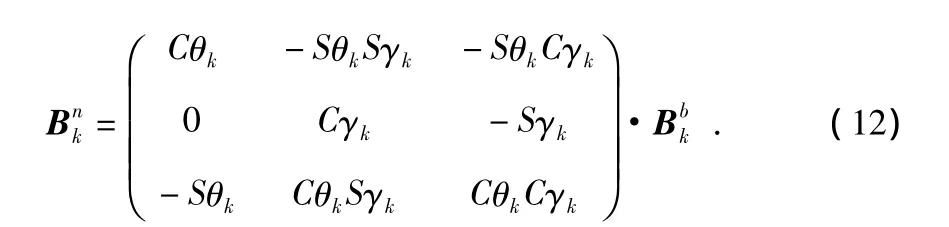
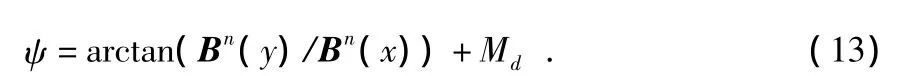
其中，ψ為航向角，Md為磁偏角。

加速度計主要用于獲得水平姿態角［7］。利用三軸MEMS加速度輸出計算得到橫搖角θ和縱搖角γ

在得到歐拉角后，可根據式(15)求解捷聯矩陣，再利用捷聯矩陣和四元數的關系式(16)得到四元數q(ε)。

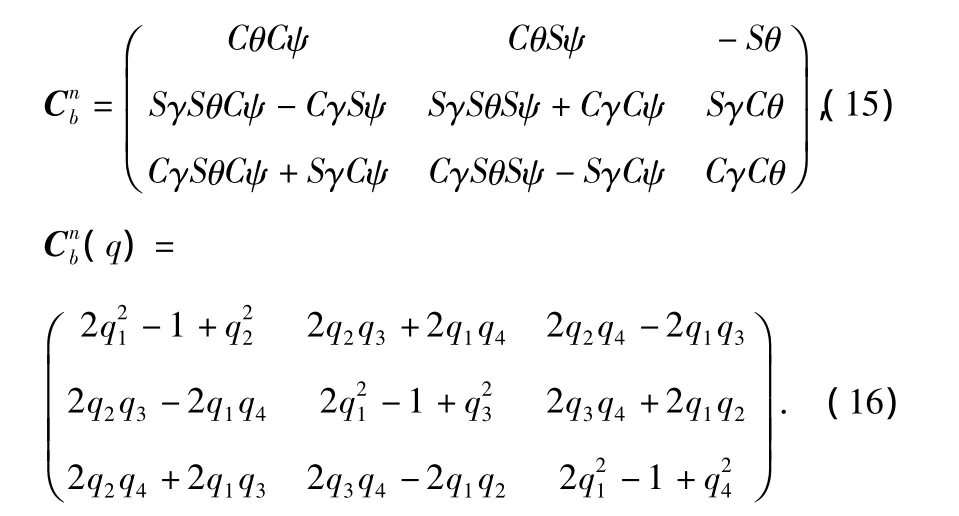
以q(w)與q(ε)之差為觀測量，實現量測更新過程。量測模型為

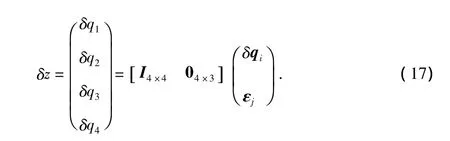
3 場地實驗

采用荷蘭Xsens公司的MTi—G型IMU進行實驗。場地為哈爾濱工程大學籃球場。首先將MIMU安裝在鞋上，并通過USB與PC連接;然后對磁力計進行標定，并采集靜態數據以獲得導航參數的初值;最后選取行走軌跡，行走時間約15 min，路程約80 m。利用谷歌地圖可得到運動軌跡如圖3所示。其中，五角星標記的曲線代表運動軌跡，三角代表開始點。

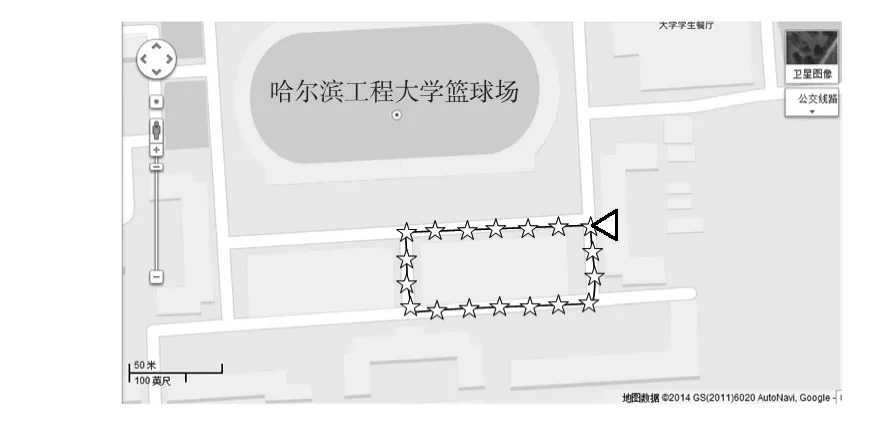
圖3 運動軌跡Fig 3 Trajectory

磁力計輸出航向和濾波后的航向對比如圖4。

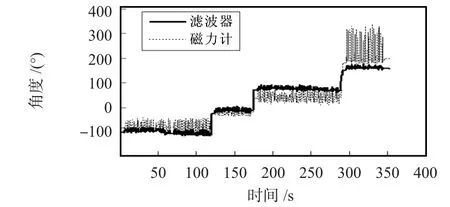
圖4 航向對比圖Fig 4 Heading comparison diagram

由圖4可以看出:磁力計輸出航向與濾波后的航向存在較大差距。在130～160 s之間磁力計輸出較為準確，由于外界磁干擾的影響，其他時間的磁力計航向波動較大。濾波后的航向更能夠反映單兵真實運動軌跡。

基于誤差四元數的數據融合算法得到的單兵運動軌跡如圖5。

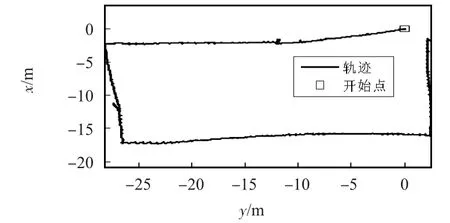
圖5 單兵運動軌跡Fig 5 Personal trajectory

由圖5和圖3對比可以看出:圖5中的運動軌跡與實驗軌跡相符，此算法能夠完成單兵定位功能。運動過程中的單兵位置誤差如表1所示。

表1 單兵位置誤差Tab 1 Personal location error

由表1可以看出:運動過程中的最大誤差為2.194 m，約占總步行距離的2.74%;平均誤差為1.269 m，約占總距離的1.58%;返回起始點時的誤差約為2.184 m，約占總距離的2.73%，故其全局誤差小于總步行距離的3%。

4 結論

本文所提的基于誤差四元數的數據融合算法充分利用了MEMS傳感器的信息，實驗證明該算法能夠對單兵進行準確定位。在無外界信號下，當步行距離為80 m時，該算法的全局誤差不超過總距離的3%，可以滿足單兵的自主定位要求。

［1］Aggarwal P，Thomas D，Ojeda L，et al.Map matching and heuristic elimination of gyro drift for personal navigation systems in GPS-denied conditions［J］.Measurement Science and Technology，2011，22(2):025205.

［2］Borenstein J，Ojeda L.Heuristic drift elimination for personnel tracking systems［J］.Journal of Navigation，2010，63(4):591-606.

［3］Renaudin V，Afzal M H，Lachapelle G.New method for magnetometers-based orientation estimation［C］∥Position Location and Navigation Symposium(PLANS)，2010 IEEE/ION，IEEE，2010:348-356.

［4］孫紅星，李德仁.非線性系統中卡爾曼濾波的一種新線性化方法［J］.武漢大學學報:信息科學版，2004，29(4):346-348.

［5］田亞軍，周 剛，胡軍照，等.捷聯慣導系統姿態算法實現及工程應用［J］.四川兵工學報，2011，32(1):10-12.

［6］Afzal M H，Renaudin V，Lachapelle G.Magnetic field-based heading estimation for pedestrian navigation environments［C］∥2011 International Conference on Indoor Positioning and Indoor Navigation(IPIN)，IEEE，2011:1-10.

［7］Luinge H J，Veltink P H.Measuring orientation of human body segments sing miniature gyroscopes and accelerometers［J］.Medical and Biological Engineering and Computing，2005，43(2):273-282.