單舷側散貨船舷側局部結構冗余度研究

陳 鵬，萬正權，劉俊杰，王 雷

(中國船舶科學研究中心，江蘇 無錫214082)

0 引 言

2009年IACS 召開的MSC86 屆會議正式提出了對船舶結構冗余度的要求。要求中規定，船舶的冗余設計和建造，應使任何加強的結構構件的局部損壞(諸如永久的局部變形，裂紋或焊縫失效)都不會導致隨之立即發生整個加強板列的損壞。同樣在solas XII 中規定，由于碰撞等原因，造成舷側局部結構出現受損或失效，船舶舷側局部結構應具有一定冗余度使得船舶具備漂浮水面或進港維修的能力［1］。冗余度與結構體系可靠性密切相關，它是提高結構可靠性的指標，是用多余資源來換取可靠性，也被稱為冗余技術［2］。結構體系可分為靜定結構和超靜定結構2 種形式。在靜定結構中，假設有一個構件失效，那么整個系統就會遭到全部破壞;但對于超靜定結構，單個構件的失效，并不一定會導致整個系統的毀壞。這在可靠性的理論中稱之為冗余系統，冗余度就是冗余系統的特征量。

針對結構冗余度的研究，土木工程行業一直致力于此，并取得了相關成果。McGuire 等［3］將結構冗余度表達為除平衡方程外求解所必需方程的個數，即將它等同于結構超靜定次數或冗余反力數目。Liao K W 等［4］研究表明，如果結構構件性能表現為脆性或者構件強度之間具有較大的相關性，那么更多的超靜定次數并不必然使結構更安全。Ang 等［5］從冗余度的反面指出，非冗余結構破壞概率等于構件的破壞概率。Kaisheng Chen［6］等曾針對海洋工程的系統冗余度進行研究，提出基于半概率方法的評估準則。相對而言，船舶行業對這方面的研究較少，而船舶舷側結構一旦出現冗余度不足，引發的危害巨大。因此，舷側局部結構在設計中應考慮冗余度要求，以使船舶在經受任何一個主要構件破壞后依然具有保持漂浮和航行能力。

冗余度的表達式很多［7］，本文采用確定性表達式，儲備冗余度因子R2定義船舶舷側局部結構冗余度，如式(1)所示。

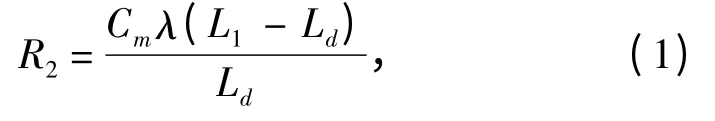
式中:L1為船舶舷側局部結構的后屈曲載荷;Ld為船舶舷側局部結構的設計載荷;λ為計算工況下載荷的安全系數;Cm為結構材料非線性修正系數。

本文首先基于冗余技術的并行原理，在三艙段分析模型的基礎上，進行單舷側散貨船舷側局部結構失效路徑判斷;接著基于后屈曲理論和非線性有限元方法，應用儲備冗余度因子R2作為結構冗余度的表達形式，對單舷側散貨船舷側局部結構冗余度進行研究。

1 后屈曲理論

對單舷側散貨船舷側局部結構這種典型的加筋板架結構進行后屈曲分析，主要基于后屈曲理論和非線性有限元方法，根據最小勢能原理，考慮材料非線性和幾何非線性影響因素，建立結構抗屈曲性能的模型，離散得到結構外載荷陣與位移陣的關系式為［8］:

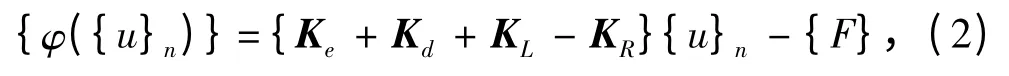
式中:Ke為結構的彈性矩陣;Kd為幾何剛度矩陣;KL為大位移矩陣;KR為載荷矯正矩陣。{φ({u}n)}為第n步的剩余載荷;{u}n為第n步的位移量;{F}為外載荷陣。在對式(2)每一子步的切線剛度進行求解后再計算步位移增量，迭代過程是基于Newton-Raphson 迭代的弧長法，迭代公式如下:

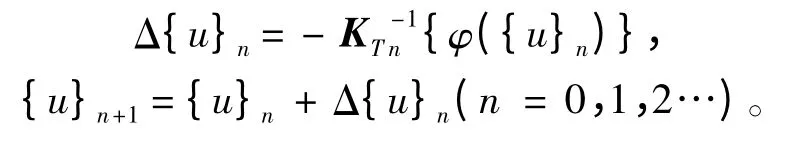
式中:KTn為第n步的切線剛度矩陣。在Newton-Raphson 迭代的弧長法的迭代過程中，能夠跟蹤整個結構的平衡路徑并獲得整個板架結構失穩過程中實際的載荷、位移關系的全部信息，進而完成板架結構的后屈曲分析。

2 算 例

2.1 舷側局部結構參數及計算模型

目標船為單舷側散貨船，屬于規范規定的BC－A 類船舶。船體采用船用Mild 普通鋼、AH32 高強度鋼、AH36 高強度鋼。船舶滿載隔艙裝載工況時，第1，3，5 貨艙裝貨，第2，4 貨艙為空艙;船舶重壓載情況下，第3 貨艙為重壓載艙，其舷側局部結構參數如表1所示。

根據失效路徑判斷及冗余度分析的需要，建立單舷側散貨船三艙段計算模型，如圖1所示。該模型縱向范圍覆蓋3個貨艙長度和4個橫艙壁。采用四節點殼單元、梁單元以及桿單元模擬上述船體結構。對于承受水壓力和貨物壓力的各類板上的扶強材用梁單元模擬，縱桁、肋板上加強筋、肋骨和肘板等主要構件的面板和加強筋用桿單元模擬。有限元網格尺寸在縱向取一個肋距，在橫向以及垂向取一個扶強材間距。模型中節點總數為195 895，單元總數為187 899。

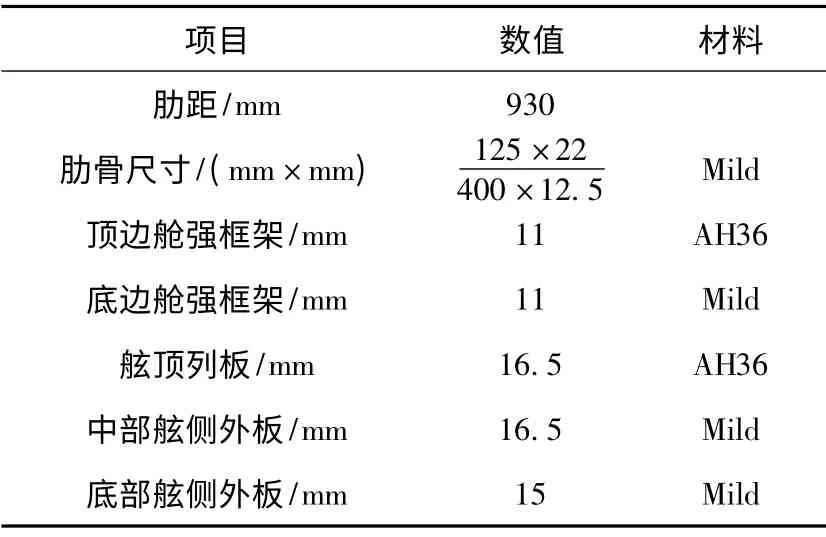
表1 舷側局部結構參數Tab.1 Side local structure parameters

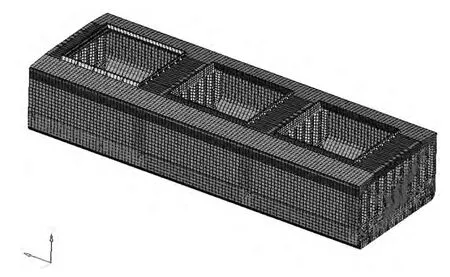
圖1 單舷散貨船三艙段計算模型Fig.1 FEA for single side bulk carrier

2.2 失效路徑判斷

散貨船舷側局部結構失效路徑判斷的方法是根據冗余技術的并行原理，找出舷側結構最危險的工況，也就是冗余度分析工況。在該工況下，觀察舷側結構的舷側列板、肋骨、舷側縱骨的應力分布，找出等效應力最大的一根骨材或列板，假定該構件已經失效，并將其刪除。刪除掉應力最大的一根骨材后，繼續進行該工況下的強度計算，并繼續刪除相應最大的等效應力的構件。通過一系列計算，可以逐步找出散貨船舷側結構局部失效路徑。

根據各工況下的強度分析可知，隔艙重貨裝載時舷側結構中的舷頂列板 (舷頂列板的材料為AH36)和肋骨(肋骨的材料為Mild)應力很大，定義該工況為舷側局部結構冗余度分析工況。本文分別假定舷頂列板首先失效和肋骨首先失效，來判斷散貨船舷側結構在冗余度分析工況下的2 種失效路徑。

假定舷頂列板首先失效，去掉中間貨艙的舷頂列板進行冗余度分析工況的強度計算，得到舷頂列板失效后舷側結構的應力云圖(見圖2)，從圖中可看出，1#和2#頂邊艙橫框架應力達到335 MPa，超過許用應力，出現局部失效。即舷頂列板失效后，1#和2#頂邊艙橫框架相繼失效。在舷頂列板失效的模型基礎上，再次去掉應力超過許用應力的2塊頂邊艙橫框架(1#和2#)，繼續進行同樣工況下的強度計算。1#和2#頂邊艙橫框架失失效后舷側結構應力云圖(見圖3)，從圖中可看出，舷側外板的應力不超過170 MPa，頂部橫框架應力不超過264 MPa，肋骨應力不超過200 MPa，即在舷頂列板，1#和2#頂邊艙橫框架相繼失效后，舷側結構不會進一步破損，失效路徑為舷頂列板失效，導致1#和2#頂邊艙橫框架。

假定肋骨首先失效，去掉中間貨艙肋骨應力最高為230 MPa的11#肋骨(肋骨編號如圖4所示)進行冗余度分析工況的強度計算。11#肋骨失效后舷側結構應力云圖(見圖5)，從圖中可看出，12#肋骨應力達到257 MPa，超過許用應力235 MPa。即11#肋骨失效后，引起12#肋骨破壞。同樣，在11#肋骨失效計算模型基礎上，去掉12#肋骨，繼續進行冗余度分析工況的強度計算。11#，12#肋骨失效后舷側結構應力云圖(見圖6)，從圖中可看出，10#肋骨應力達到283 MPa，超過許用應力235 MPa。即11#，12#肋骨相繼失效后，引起10#肋骨破壞。同樣，在11#，12#肋骨失效計算模型基礎上，去掉10#肋骨，繼續進行冗余度分析工況的強度計算。11#，12#，10#肋骨失效后舷側結構應力云圖(見圖7)，從圖中可看出，9#肋骨應力達到283 MPa，超過許用應力235 MPa，且舷側外板應力達到358 MPa，超過許用應力326 MPa，即，11#，12#，10#肋骨相繼失效后，引起9#肋骨破壞和舷側外板同時破壞。

圖2 舷頂列板失效后舷側應力云圖Fig.2 Stress after the sheer strakes failure

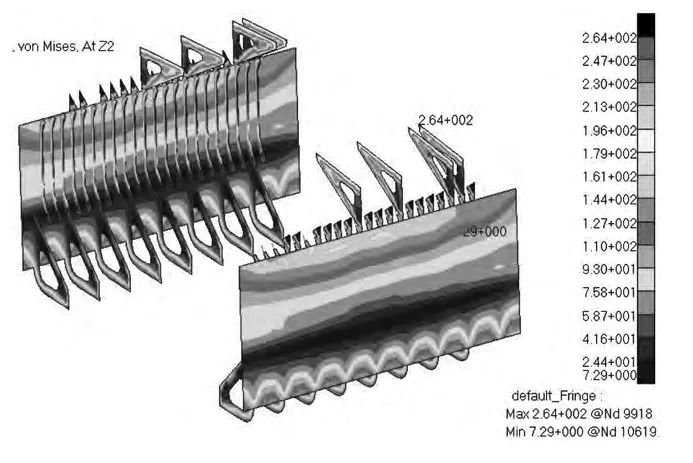
圖3 1#和2#頂邊艙橫框架失失效后舷側應力云圖Fig.3 Stress after the 1#～2# top tanks framework failure

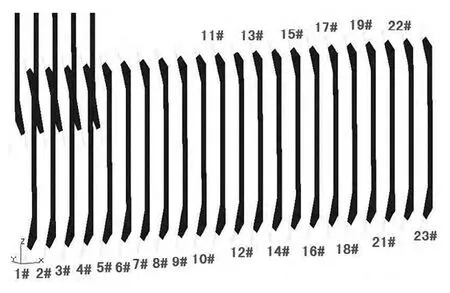
圖4 肋骨編號Fig.4 Frame number

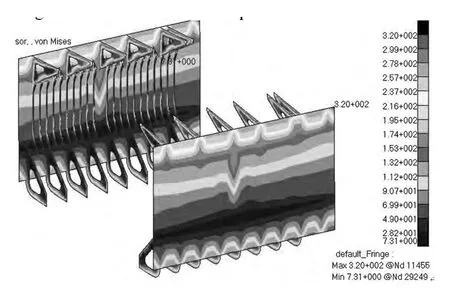
圖5 11#肋骨失效后舷側應力云圖Fig.5 Stress after the 11# frame failure

圖6 11#，12#肋骨失效后舷側應力云圖Fig.6 Stress after the 11# and 12# frame failure

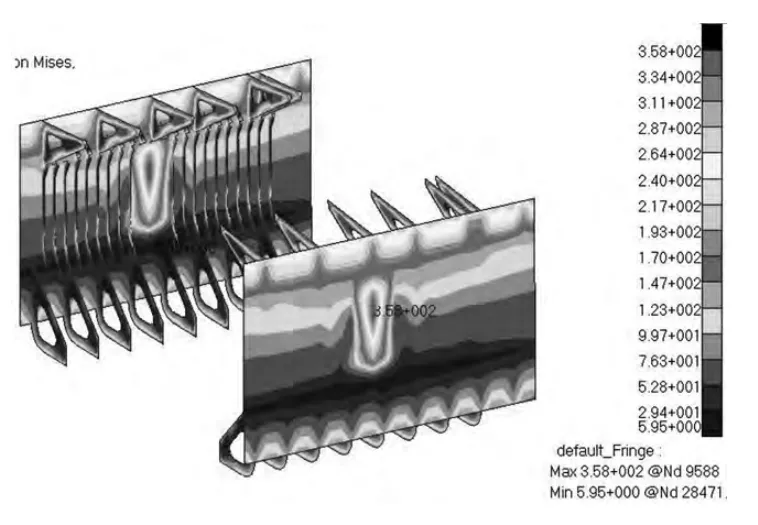
圖7 11#，12#和10#肋骨失效后舷側應力云圖Fig.7 Stress after the 11# ，12# and 10# frame failure

根據以上計算分析，可以初步判斷散貨船舷側局部結構在相應工況下的失效路徑。第1 條失效路徑為:舷頂列板首先失效，導致1#和2#頂邊艙強肋骨失效，進而失效路徑終止，舷側結構不會進一步破壞;第2 條失效路徑為:11#肋骨首先失效，進而導致12#肋骨失效，最后導致10#肋骨失效，并同時引起舷側外板破裂，致使舷側結構發生整體垮塌。由以上分析可知，第2 條失效路徑，即肋骨首先失效路徑，會引起舷側結構整體失效，造成更大的危害;目標船的舷側局部結構冗余度不滿足要求。

2.3 后屈曲分析

建立單舷散貨船舷側局部結構后屈曲計算模型，如圖8所示。為準確反映局部舷側局部結構在相應工況下的后屈曲狀態，本文選擇對舷側局部結構偏于危險的冗余度分析工況，提取相應位置處的節點位移和力，并施加在后屈曲計算模型上。目標船隔艙裝載工況的設計彎矩為1 655 632.5 kNm。

選擇合適的參數，利用弧長法進行迭代計算。施加相應工況的邊界條件，設置20個子步，限制最大迭代弧長為1。從計算結果看出，舷側局部結構的臨界計算彎矩為2 582 785.9 kNm。舷側局部結構計算彎矩與位移曲線，如圖9所示。單舷側散貨船舷側局部結構不同計算彎矩作用下的位移云圖，如圖10所示，從位移云圖中可以看出舷側結構破壞形式與靜強度計算的破壞路徑類似:均為中間肋骨首先失效，并引起舷側外板失效，最終導致舷側局部結構整體垮塌。

圖8 舷側局部結構后屈曲計算模型Fig.8 Post-buckling model for side local structure

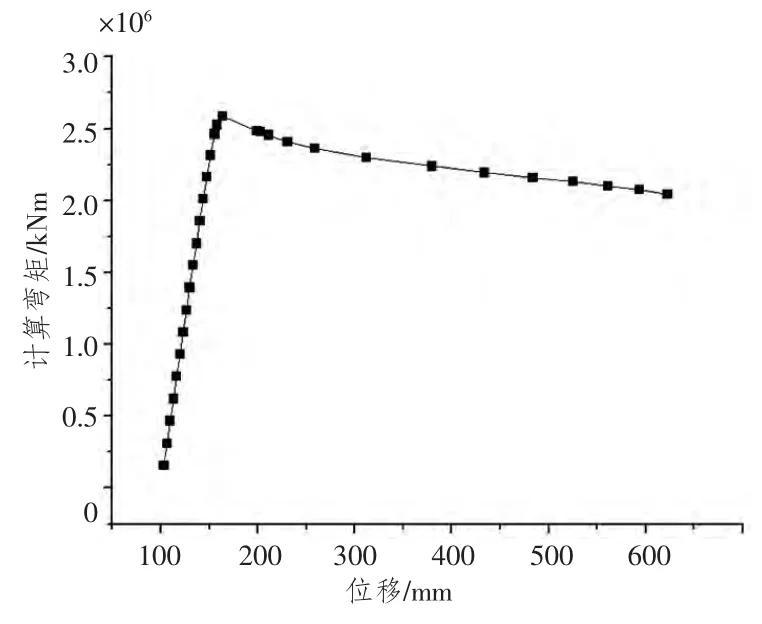
圖9 舷側局部結構計算彎矩－位移曲線Fig.9 Calculating bending moment-displacement curves for side local structure

圖10 散貨船舷側局部結構各階段位移云圖Fig.10 Each load step displacement contours for side local structure

通過后屈曲分析得到單舷側散貨船型舷側局部結構臨界彎矩L1為2 582 785.9 kNm，而舷側冗余度分析工況的設計彎矩為Ld為1 655 632.5 kNm，根據式(1)目標船舷側局部結構冗余度為:R2=0.92，其中λ = 1.4，Cm= 1.17。根據文獻，冗余度R2＞1 即可認為結構具有一定的冗余度［9］。目標船舷側局部結構冗余度不滿足要求，與本文失效路徑判斷的結果一致。

3 結 語

1)本文基于冗余技術的并行原理，對單舷側散貨船舷側局部結構失效路徑判斷進行判斷。初步得到目標船型的2 條失效路徑:第1 條為舷頂列板首先失效，導致1#和2#頂邊艙強肋骨失效，進而失效路徑終止，舷側結構不會進一步破壞。第2 條為11#肋骨首先失效，進而導致12#肋骨失效，最后導致10#肋骨失效，并同時引起舷側外板破裂，致使舷側結構發生整體垮塌。

2)本文基于后屈曲理論和非線性有限元方法，應用儲備冗余度因子R2作為結構冗余度的表達形式，對單舷側散貨船舷側局部結構進行冗余度計算。結果表明目標船舷側局部結構冗余度不滿足要求，與本文失效路徑判斷的結果一致;得到的舷側結構破壞形式與本文計算的失效路徑類似。該方法可為船舶舷側局部結構的冗余度分析和設計提供參考。

［1］IMO.International Convention for the Safty of Life at Sea.International Maritime Organization.2011.

［2］柳承茂，劉西拉.基于剛度的構件重要性評估及冗余度的關系［J］.上海交通大學學報，2005，39(5):746－750.LIU Cheng-mao，LIU Xi-la.Stiffness-based evaluation of component Importance and its relationship with redundancy［J］.Journal of Shanghai Jiaotong University，2005，39(5):746－750.

［3］MCGUIRE W，GALLAGHER R.Matrix structural analysis［J］.New York:Wiley＆Sons，1979.

［4］LIAO K W，WEN Y K，et al.Evaluation of 3D steel moment frames under earthquqke excitations Ⅱ:reliability and redundancy［J］.Journal of Structural Engineering，ASCE，2004，133(3):471－480.

［5］ANG A，TANG W.Probability concepts in engineering planning and design［J］.New York:John Wiley＆Sons，1984(2).

［6］CHEN Kai-sheng，ZHANG Sheng-kun.Semi-probabilistic method for evaluating system redundancy of existing offshore sturures［J］.Ocean Engineering，1996，23(6).

［7］FRANGPOL D M，JAMES P C.Effects of damage and redundancy on structural reliabilty［J］.Journal of structure Engineering，2007，113(7).

［8］BISAGNI C，VESCOVINI R.Analytical formulation for local buckling and post-buckling analysis of stiffened laminated panels［J］.Thin-Walled Structures，2009，47:318－334.

［9］HUSAIN M，TSOPELAS P.Measures of structural redundancy in reinforced concrete buildings.Ⅰ:Redundancy Indices［J］.Journal of Structural Engineering，ASCE，2004，130(11):1651－1658.