基于改進粒子濾波的射頻識別室內跟蹤算法

石雪軍，紀志成

（江南大學物聯網工程學院，江蘇無錫214122）

基于改進粒子濾波的射頻識別室內跟蹤算法

石雪軍，紀志成

（江南大學物聯網工程學院，江蘇無錫214122）

針對復雜室內環境下移動目標難以跟蹤和粒子濾波容易喪失粒子多樣性的問題，提出一種射頻識別室內跟蹤算法。將讀寫器接收到的信號強度指示樣本值直接作為觀測量建立非線性狀態空間模型，給出一種帶有馬爾科夫鏈蒙特卡洛（MCMC）移動步驟的改進部分系統重采樣算法，采用度量函數實現粒子集分類并進行重采樣處理加入MCMC移動步驟，增加粒子多樣性。應用該濾波算法對非線性單變量靜態模型和上述非線性跟蹤模型進行仿真，并與其他重采樣濾波算法進行比較，實驗結果表明，該濾波算法的濾波性能更好，跟蹤精度更佳。

射頻識別；室內跟蹤；粒子濾波；馬爾科夫鏈蒙特卡洛；部分系統重采樣；度量函數

1 概述

近年來，隨著物聯網技術的蓬勃發展，基于位置信息的服務被普遍認為是一項不可或缺的關鍵技術，這些位置服務需要對復雜室內環境，如大型超市、地下停車場等進行精確定位；人們對室內移動目標位置的跟蹤需求也與日俱增，礦井、倉庫等都需要準確的目標跟蹤，以實現用戶對庫存物資和可用空間的高效管理，室內無線跟蹤技術正是基于此原因而出現并逐漸成為研究熱點。有效的定位技術是位置跟蹤服務的基礎，目前常見的室內定位技術主要有超聲波、藍牙等，但室內環境中存在的多徑效應［1］、非視距［2］等因素將會嚴重影響室內目標的定位精度。

射頻識別（Radio Frequency Identification，RFID）是一種利用射頻信號通過空間耦合實現非接觸式雙向通信并通過所傳遞的信息達到自動識別和定位目的的技術，具有極強的抗干擾能力和穿透性能；存儲在標簽內的數據可以進行加密保護，數據記憶容量大，在跟蹤定位過程中可以提供豐富的信息，因此，在室內位置服務中，RFID具有很大的優勢［3］。目前定位算法分為測距和非測距2種，其中測距定位需要周圍節點提供距離或方位信息，如信號到達時間（Time of Arrival，TOA）、信號到達角（Angle of Arrival，AOA）和接收信號強度指示（Received Signal Strength Indication，RSSI）等，和非測距如近似三角形內點測試法、質心算法相比，這類算法對硬件要求高、能耗大，但具有較好的跟蹤性能。由于RSSI定位方法是利用已有的無線傳感網絡設備和移動終端完成定位，無需額外的網絡消耗和硬件支持，因此對基于RFID的位置服務，該方法十分適用［4］。

跟蹤移動目標的位置信息時，為了使系統具有實時性，一般要在較短時間內估算出移動目標當前的位置，雖然RFID技術讀取數據方便、識別速度快，但在進行實時跟蹤時，閱讀器獲取的射頻信號強度樣本較少，此時直接計算移動目標位置得到的估算值方差較大，嚴重影響了定位精度。

本文通過研究粒子濾波，結合室內無線信道的特點對室內運動目標進行跟蹤，針對粒子退化［5］和貧化［6］現象，提出一種改進的部分系統重采樣粒子濾波算法。

2 問題描述

2.1 RSSI測距原理

在基于RSSI測距技術中，首先需要獲得RFID標簽的信號發射功率和閱讀器接收功率，將兩者差值作為無線射頻信號在傳輸過程中的能量損耗值，根據對數分布傳播損耗經驗模型［7］將其轉化為空間距離，當給定距離為d時，所有路徑損耗的平均值為：

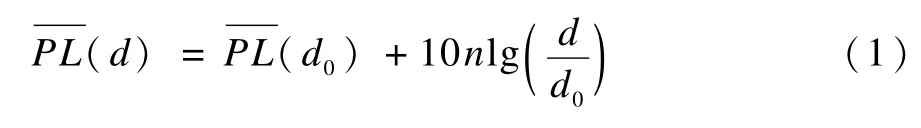
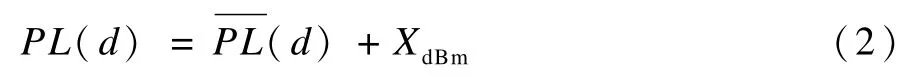
其中，X是一個以dBm為單位，平均值為0的高斯隨機變量，反映了當距離一定時，接收能量的變化。因此，RFID閱讀器的接收功率為：

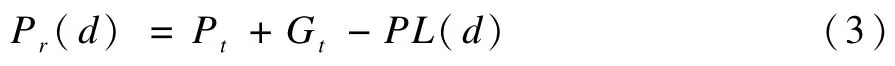
其中，Pr（d）為閱讀器接收信號強度；Gt為RFID標簽天線增益；Pt為發射裝置發射功率，單位均為dBm。

在式（1）～式（3）中，路徑損耗系數n、發射功率Pt和天線增益Gt均已知，閱讀器接收功率Pr（d）也易測量，從而可以計算出標簽和閱讀器間的距離d，再根據三邊測量算法［8］就可以推算出移動目標的位置。

2.2 RFID室內跟蹤系統模型

考慮一般的室內移動目標跟蹤問題，采用有源電子標簽作為被跟蹤目標，閱讀器作為RFID信號檢測源，如圖1所示，閱讀器采用等邊三角形［9］網格布局，即標簽在任何位置都能被至少3個閱讀器同時識別。

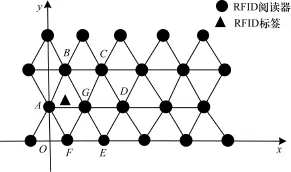
圖1 RFID閱讀器網格分布

假設帶有RFID標簽的移動目標在二維平面上運動，跟蹤模型中的狀態方程和觀測方程可表示如下：

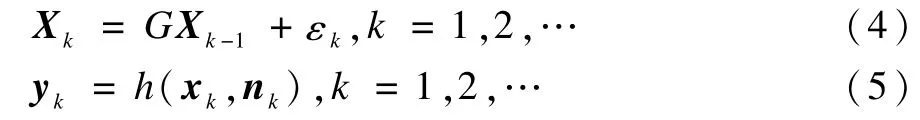
其中，向量xk=［xk，vxk，yk，vyk］T為k時刻運動目標的狀態矢量；（xk，yk）和（vxk，vyk）分別表示k時刻的位置坐標和x，y軸方向上的速度分量；εk為相應的系統噪聲；yk=［s1，s2，…，sn］表示k時刻的觀測矢量si（i=1，2，…，n）表示第i個RFID閱讀器接收到的信號強度值；nk為觀測噪聲。

3 改進的粒子濾波跟蹤算法

3.1 標準粒子濾波

粒子濾波（Particle Filtering，PF）［10］是一種基于蒙特卡洛模擬仿真的遞推貝葉斯估計方法，適用于任何狀態空間模型，能有效地解決非線性、非高斯噪聲環境下的狀態估計問題，算法基本步驟如下［11］：

（1）粒子初始化

從先驗概率密度函數p（x0）中產生粒子樣本集｛xi0｝Nsi=1，令k=0，所有粒子權值均為1/Ns。

（2）預測

令k=k+1，在未得到k時刻的觀測值時，由狀態轉移概率密度p（xk|xik-1）從粒子集｛xik｝Nsi=1中抽取Ns個新粒子，即通過產生噪聲來得到新粒子。

（3）更新

利用當前測量值yk對先驗狀態估計p（xk|y1：k-1）進行修正，得到當前時刻的后驗概率分布p（xk|y1：k），每個新粒子的權值可由式（6）和式（7）進行計算。

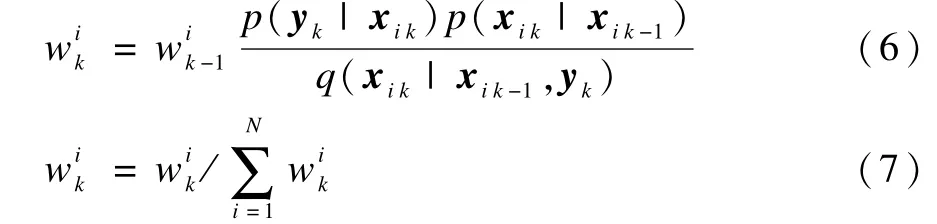
因觀測模型具有馬爾科夫性［12］，濾波時歷史狀態和觀測值均無需保存，所以后驗概率分布近似為：

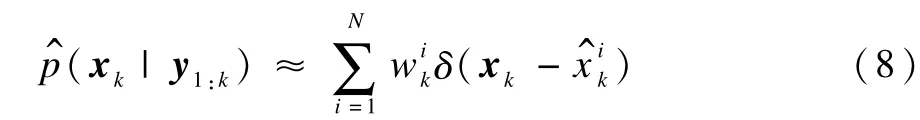
（4）重采樣

在k時刻采樣得到新粒子并更新對應的權值后后驗概率密度函數如式（8）所示，重采樣就是在該分布中根據的原則重新采樣Ns次得到新粒子集，且新粒子的權值均為1/Ns。

（5）狀態估計

由更新階段可知后驗概率分布可近似為式（8）的形式，則狀態向量的估計值為：

由式（8）和式（9）得狀態估計：

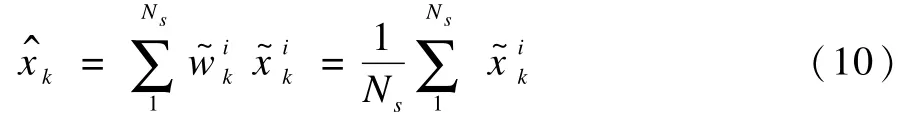
令k=k+1，返回步驟（2）。

3.2 改進的部分系統重采樣算法

粒子濾波在非線性和非高斯系統中表現出來的優越性決定了其應用范圍十分廣泛［13-14］，但其本身存在一個嚴重的缺陷，即粒子退化。重采樣是解決粒子退化的主要方法，然而傳統的重采樣算法都是基于分層采樣方法的，如多項式重采樣、殘差重采樣、系統重采樣等［15］，其中系統重采樣就是通過簡單地比較粒子權重和均勻分布的隨機數之間的大小，消除權重較小的粒子，繁殖權重較大的粒子，這樣會導致一些權重較大的粒子可能會被丟棄，同時一些權值較小的粒子會被保留下來；其次，對權重較大的粒子直接復制而不是產生新粒子，這樣很容易出現樣本貧化。因此，提出一種改進的部分系統重采樣算法，采用一個表征粒子退化程度的度量函數來改進傳統的系統重采樣算法，與其相似的是，在新的重采樣算法中首先生成2個序列：

第1個序列為粒子權值累積分布函數，記為｛Ci，i=1，2，…，Ns｝，其公式如下所示：

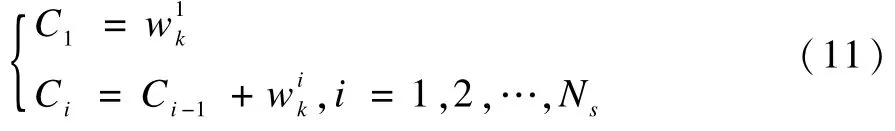
第2個序列為權值參考函數，記為｛rj，j=2，3，…，Ns｝，其公式如下所示：

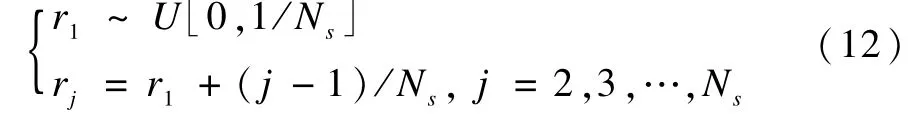
其中，r1為［0～1/Ns］之間均勻分布的隨機數。

圖2形象地說明了2個序列之間的關系。其中，圓形粒子屬于集合1；方形粒子屬于集合2；三角形粒子屬于集合3。豎線和橫線分別表示序列｛Ci｝和｛rj｝，通過比較序列｛Ci｝和｛rj｝，產生用于表征粒子退化程度的測量函數M（i），函數M（i）偽代碼如下所示：

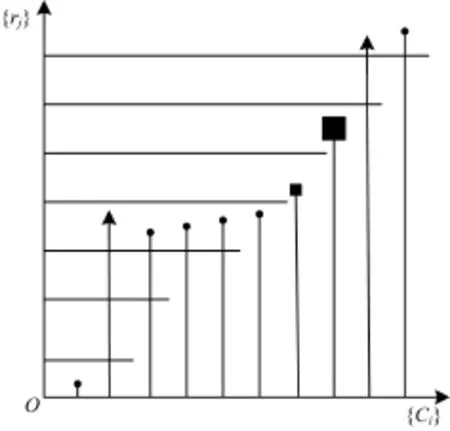
圖2 粒子權值分析圖

測量函數M（i）包含了粒子權重信息，可以將其認為是粒子權重的非線性變換。當粒子權重增加時，M（i）的數值會變大，然而當粒子權重減小時，M（i）的數值會變小。根據粒子權重的大小，測量函數M（i）的值為0、1或者大于1的數，i=1，2，…，Ns。

因此，新重采樣算法不是簡單地通過對比序列｛Ci｝和｛rj｝來復制或者丟棄粒子，而是采用測量函數M（i）將粒子分類并進行相應處理。根據M（i）的數值可以將粒子分為3個集合：

（1）集合1：M（i）=0表示當前粒子的權值很小，和在它們之前的第1個粒子位于同一區間內，這些粒子被直接丟棄。

（2）集合2：M（i）=1表示當前粒子的權值大小中等，和在它們之前的第1個粒子不同，該粒子位于下一個區間內。將這些粒子跟它們前面第1個測量函數值為非0的粒子相比，如圖2所示，權值較大的粒子被保留而權值較小的粒子被淘汰，即：

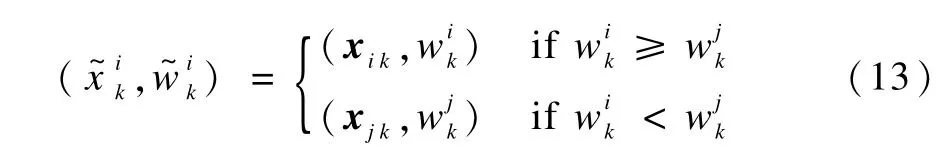
其中，M（j）≠0 and j＜i。

（3）集合3：M（i）＞1表示當前粒子的權值比較大，其所在的區間與它們前面的粒子所在的區間不相鄰，和集合1、集合2中的粒子相比，這些粒子更加靠近真實值。最簡單的方法就是直接復制這些權值較大的粒子，但是這種方法可能會導致粒子貧化；如果將其作為母粒子用于產生新粒子又會減緩收斂速度。為了解決這種問題，提出使用一個門限值Wth將集合3中的粒子分為集合3a和集合3b 2個子集，把權值足夠大的粒子歸入集合3a，權值次大的粒子存入集合3b。在圖2中，較大的三角形粒子屬于集合3a，另一個三角形粒子屬于集合3b。

保留集合3a中的粒子并按以下方式進行復制：

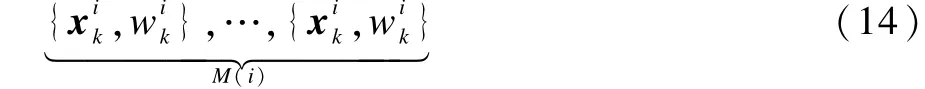
其中，M（i）表示粒子復制的次數，各粒子相應的權值在復制過程中保持不變。

集合3b中的粒子被作為母粒子用于產生新的子粒子，當M（i）是基數時則新粒子的產生方式如式（15）所示：

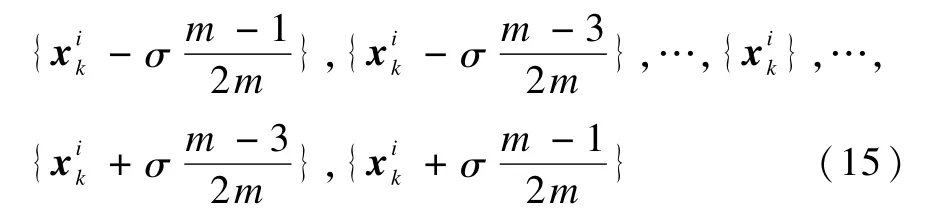
相反，如果M（i）是偶數，那么新粒子產生方式如式（16）所示：

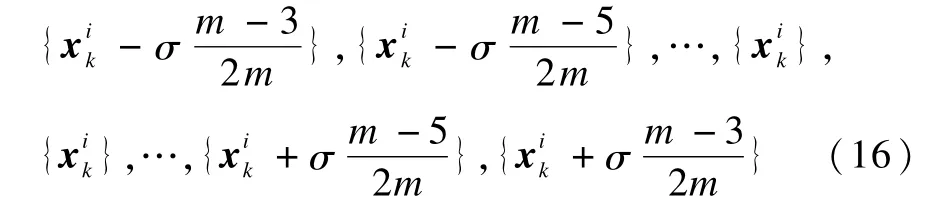
其中，m=M（i）；σ為誤差，表示新生成的子粒子之間的密集程度。新粒子分布在母粒子的兩側，它們對應的權值為：

N個重采樣粒子和其對應的權值可由上述方法獲得，但是可能會出現某些粒子沒有產生子粒子而有些粒子會產生大量的后代，這樣就喪失了粒子的多樣性，影響濾波器的性能，為此加入一個MCMC移動步驟［16］來增加粒子的多樣性，步驟如下：

Step1 從建議分布函數p（xk|xik-1）中采樣生成備用粒子，即：

Step2 產生一個（0，1）范圍內服從均勻分布的隨機數作為參考接收系數vi，則：

Step3 按照式（20）計算真實接收系數，即：

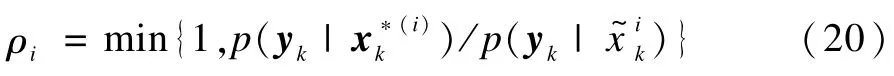
Step4 如果ρi≤vi，則按以下方式接收該移動步驟：

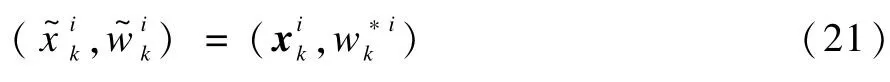
否則，拒絕該移動步驟，即：

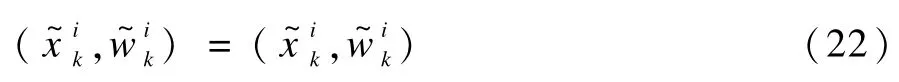
Step5 歸一化權值，獲得新粒子：

為了避免繁瑣的離線測量過程，本文采用對數正態分布模型來描述信號接收強度，選擇狀態轉移概率密度分布作為建議分布，如果將k-1時刻的粒子記為，則k時刻的粒子可由式（5）得到。粒子是對標簽的模擬，每個粒子都代表了移動標簽可能的位置，此時粒子權值更新公式為：

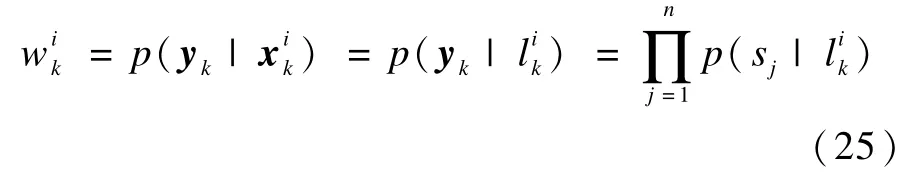
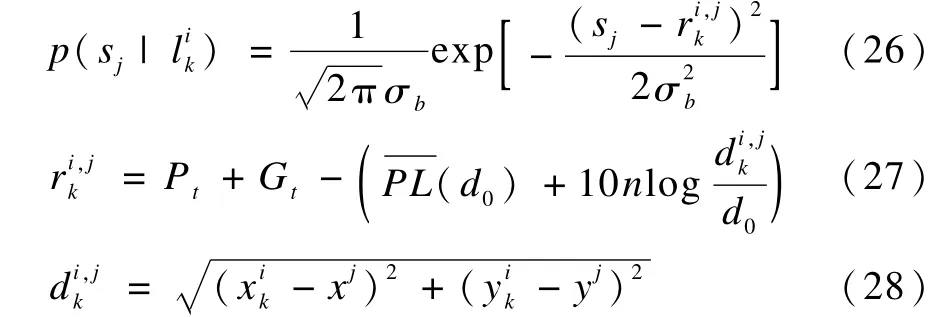
4 仿真結果與分析

實驗1 改進算法與系統重采樣算法性能比較

為了驗證改進部分系統重采樣算法的有效性，考慮文獻［6］中的非線性單變量靜態模型：

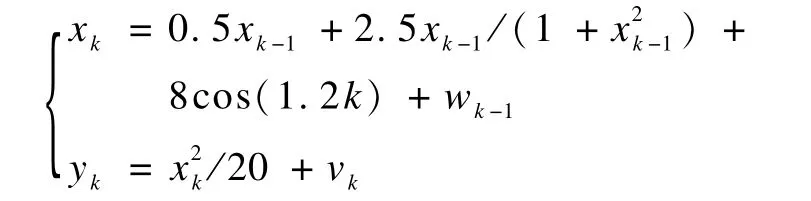
其中，系統噪聲wk和觀測噪聲vk為均值為0、方差分別為Qk=10和Rk=1的高斯噪聲，即wk～N（0，Qk），vk～N（0，Rk），狀態初值x0=0，仿真步數設為50。

圖3是隨時間變化，改進部分系統重采樣和統系統重采樣算法的狀態估計與真實的運動軌跡之間的比較曲線。

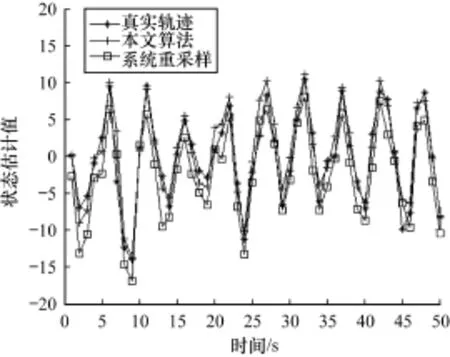
圖3 狀態估計曲線

圖4 給出了三者之間狀態估計的誤差標準差曲線，從中可以看出，本文提出的重采樣算法精度較傳統重采樣算法有所改善，這可解釋為系統重采樣算法是完全重采樣，導致大量的低權值潛力粒子消失，有損濾波精度，而本文提出的部分系統重采樣算法很好地避免了這一問題。

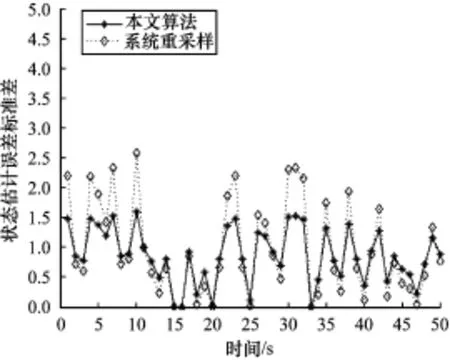
圖4 狀態估計的誤差標準差曲線

實驗2 不同濾波器的室內目標跟蹤性能分析

通過M atlab對本文提出的改進粒子濾波RFID室內跟蹤算法進行仿真實驗。參數設置如下：參考距離d0=1 m，環境系數n=2，目標的初始狀態X0=［0，1，0，1］T，假定系統噪聲和觀測噪聲的協方差分別為Q=diag（［0.01，0.01］）和R=2，誤差σ= 0.25，標準差σb=1，采樣時間T=1 s，粒子數N= 100，門限值Nth=0.75Ns，Wth為最大粒子權值，共進行10次蒙特卡洛實驗。

下面分別給出系統重采樣粒子濾波、自適應部分系統重采樣粒子濾波［17］和本文提出的改進部分系統重采樣粒子濾波移動目標的跟蹤性能比較。

圖5和圖6分別顯示了移動目標的位置和速度估計誤差，在100個采樣周期內，改進的部分系統重采樣濾波算法、系統重采樣濾波算法和自適應部分系統重采樣濾波算法的位置和速度估計誤差分別為0.377 1 m，3.333 8 m，1.528 8 m和0.341 4 m/s，1.945 2 m/s和0.879 5 m/s。

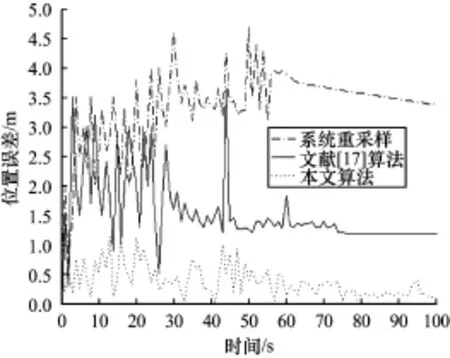
圖5 室內移動目標位置誤差

從圖5和圖6中可以看出，本文提出的改進部分系統重采樣粒子濾波算法的跟蹤精度相對最好，傳統重采樣濾波器性能最差。這是因為傳統系統重采樣濾波算法可能會丟棄一些權重較大的粒子，與此同時權值較小的一些粒子會被保留下來；它只是簡單地對權重較大的粒子直接進行復制而不是產生新粒子，很容易使粒子失去多樣性；文獻［17］中的濾波器對粒子進行部分重采樣處理，有助于緩解粒子貧化問題，但效果有限，而本文提出的改進濾波在對粒子進行部分重采樣的基礎上加入了MCMC移動步驟，提高了粒子細化能力，增加了粒子的多樣性，有效改善了RFID室內移動目標的跟蹤性能。

表1給出了100個采樣周期內，3種濾波算法的位置和速度估計誤差的統計結果。和其他2種濾波器相比，改進的部分系統重采樣濾波算法的跟蹤性能相對最好。

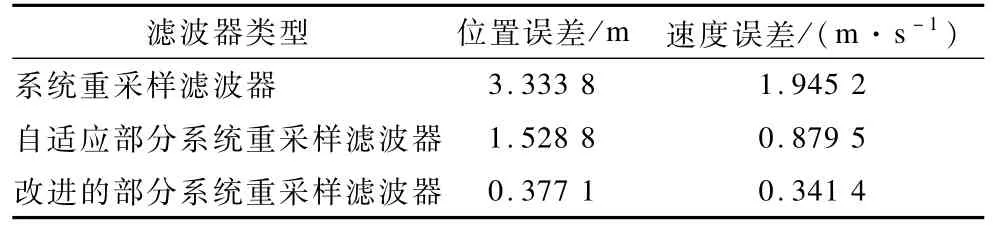
表1 3種濾波器的跟蹤性能

表2和表3分別從定性和定量的角度分析了3種濾波器的時間復雜度和空間復雜度。U表示生成的隨機數，n表示第幾次循環，k表示粒子被分解的次數，i1：Ns表示各粒子最終被分解的個數。Nh1和Nh2分別表示2種算法中需要重采樣的粒子數，Sh1表示部分需要重采樣的粒子的權值和，wl和wh分別表示權值下限和上限值。

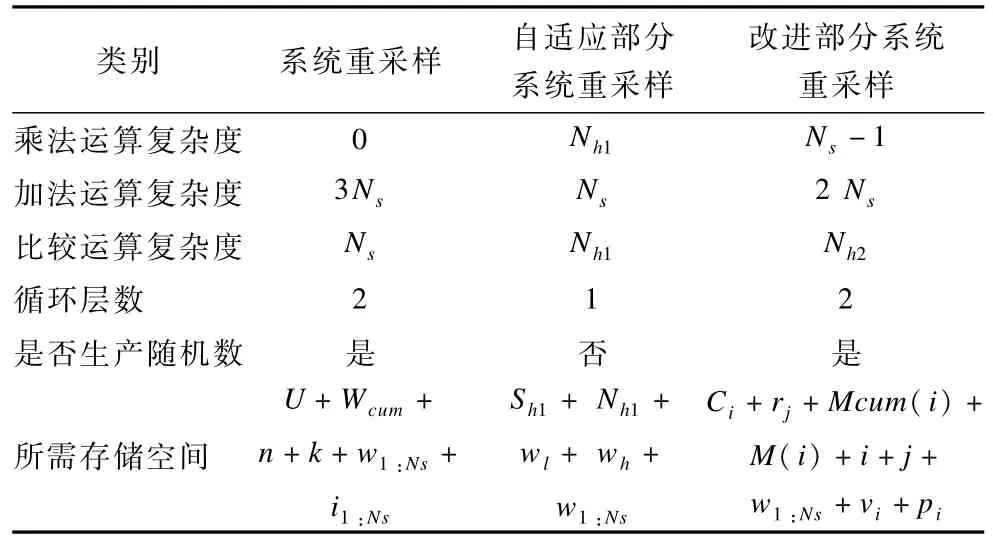
表2 3種濾波器的運算性能分析

表3 3種濾波器的運行時間s

由表2和表3的分析不難看出，文獻［17］中的濾波算法和本文提出的重采樣濾波算法均比系統重采樣濾波算法運行時間短，這是因為它們在重采樣階段只需要部分粒子參加重采樣過程，這不僅緩解了粒子貧化問題而且降低了計算執行時間；但本文提出的改進濾波算法相比文獻［17］中的算法運行時間稍長而且空間復雜度最高，這是因為本文算法對隨機數的計算較為復雜并且加入了馬爾科夫鏈蒙特卡洛移動，需要更復雜的步驟。改進的部分系統重采樣算法復雜度反而增加了。

5 結束語

本文對粒子濾波技術進行詳細研究，結合RFID室內定位技術，提出一種改進的粒子濾波RFID室內跟蹤算法。該算法將讀寫器接收到的RSSI樣本值直接作為觀測量建立非線性空間模型，將帶有MCMC移動步驟的部分系統重采樣算法應用到RFID室內移動目標定位跟蹤過程中。和其他濾波算法相比，該算法克服了重采樣后粒子貧化嚴重的問題，有效改善了粒子濾波性能，取得了較好的目標跟蹤精度，為解決復雜室內環境下移動目標難以跟蹤的問題，提供了一種有效的解決方案。然而本文算法存在占用存儲空間大、運算時間較長的問題，當使用大量粒子濾波時，濾波時效性會變差，如何提高濾波實時性、減少計算量將是今后研究的重點。

［1］ Ahmed B T.Multipath Effect on the WCDMA Uplink Capacity of Highways Cigar-shaped Microcells with Users within Cars and Buses［J］.Wireless Personal Communications，2013，71（3）：1649-1662.

［2］ Tai C S，Tan S Y，Seow C K.A Robust Non-line-of sight Localization System in an Indoor Environment［J］. Electronics Letters，2010，46（8）：593-595.

［3］ 李 程，錢松榮.射頻識別動態定位方法［J］.通信學報，2013，34（4）：144-148.

［4］ Zhou Junyi，Shi Jing.RFID Localization Algorithm s and Applications——A Review［J］.Journal of Intelligent Manufacturing，2009，20（6）：695-707.

［5］ Hong Shaohua，Shi Zhiguo，Wang Lin，et al.Adaptive Regularized Particle Filter for Synchronization of Chaotic Colpitts Circuits in an AWGN Channel［J］.Circuits，System s，and Signal Processing，2013，32（2）：825-841.

［6］ 左軍毅，張怡哲，梁 彥.自適應不完全重采樣粒子濾波器［J］.自動化學報，2012，38（4）：647-652.

［7］ 陳得昌，吳介軍，王慶林，等.基于粒子濾波的RFID室內節點定位跟蹤研究［J］.信息技術，2011，（8）：77-80.

［8］ 高 雷.基于三邊測量的分簇目標跟蹤算法［J］.計算機應用，2014，34（6）：1578-1581.

［9］ 朱 劍，趙 海，孫佩剛，等.基于RSSI均值的等邊三角形定位算法［J］.東北大學學報：自然科學版，2007，28（8）：1094-1097.

［10］ Zuo Junyi，Jia Yingna，Zhang Wei，et al.Particle Filter with Importance Density Function Generated by Updated System Equation［J］.Journal of Central South University，2013，20（10）：2700-2707.

［11］ 宋越明.基于粒子濾波的跟蹤方法研究［D］.鄭州：解放軍信息工程大學，2010.

［12］ 任子暉，王 堅，高岳林.馬爾科夫鏈的粒子群優化算法全局收斂性分析［J］.控制理論與應用，2011，28（4）：462-466.

［13］ Yan Zhenya，Zheng Baoyu，Xu Li，et al.Collaborative Tracking via Particle Filter in Wireless Sensor Networks［J］.Journal of Electronics，2008，25（3）：311-318.

［14］ Wang Yongli，Qian Jiangbo.Measuring the Uncertainty of RFID Data Based on Particle Filter and Particle Swarm Optimization［J］.Wireless Networks，2012，18（3）：307-318.

［15］ 馮 馳，王 萌，汲清波.粒子濾波器重采樣算法的分析與比較［J］.系統仿真學報，2009，21（4）：1101-1105.

［16］ Fan Y，Peters G W，Sisson S A.Automating and Evaluating Reversible Jump MCMC Proposal Distributions［J］. Statistics and Computing，2009，19（4）：409-421.

［17］ 劉文靜，于金霞，湯永利.粒子濾波自適應部分系統重采樣算法研究［J］.計算機應用研究，2011，28（3）：912-914.

編輯 顧逸斐

Radio Frequency Identification Indoor Tracking Algorithm Based on Improved Particle Filtering

SHI Xuejun，JI Zhicheng
（School of Internet of Things Engineering，Jiangnan University，Wuxi 214122，China）

To address the problem that mobile target is difficult to track in complex indoor environment and the particle diversity is losing after the resampling step，a Radio Frequency Identification（RFID）indoor tracking algorithm is proposed.It treats Received Signal Strength Indication（RSSI）sample values received by readers as observation parameter directly to establish a nonlinear state space model，while a new adaptive partial systematic resampling algorithm with Markov Chain Monte Carlo（MCMC）move step is presented.The new algorithm resamples after classifying the particles with a measure function and the MCMC move step is joined after resampling steps to improve the diversity of particles. Applying this proposed algorithm to simulate the nonlinear single variable static model and nonlinear tracking model mentioned above，and com pared with other resampling algorithms，the results show that the new algorithm has a better filtering performance and tracking accuracy.

Radio Frequency Identification（RFID）；indoor tracking；Particle Filtering（PF）；Markov Chain Monte Carlo（MCMC）；partial systematic resampling；measure function

石雪軍，紀志成.基于改進粒子濾波的射頻識別室內跟蹤算法［J］.計算機工程，2015，41（11）：308-313.

英文引用格式：Shi Xuejun，Ji Zhicheng.Radio Frequency Identification Indoor Tracking Algorithm Based on Improved Particle Filtering［J］.Computer Engineering，2015，41（11）：308-313.

1000-3428（2015）11-0308-06

A

TP301.6

10.3969/j.issn.1000-3428.2015.11.053

國家“863”計劃基金資助項目（2013AA 040405）。

石雪軍（1989-），男，碩士，主研方向：射頻識別，控制理論與控制工程；紀志成，教授、博士、博士生導師。

2014-09-18

2014-11-29 E-m ail：956003055@qq.com