基于漸進迭代逼近的平面曲線等距線算法

陳 青，潘日晶

（福建師范大學數學與計算機科學學院，福州350007）

基于漸進迭代逼近的平面曲線等距線算法

陳 青，潘日晶

（福建師范大學數學與計算機科學學院，福州350007）

針對傳統平面曲線等距線求解算法在適應性、誤差控制等方面存在的問題，基于漸進迭代逼近方法提出一種新的平面曲線等距線算法。通過基曲線上點的切矢轉角對基曲線進行自適應采樣，得到一條逼近等距線的折線，將曲線與曲線的逼近問題轉化為折線與曲線的逼近問題。在充分反映基曲線形狀特征的前提下盡可能減少采樣點數量。選取等距線上的特征點作為主控制點，利用漸進迭代逼近方法插值所選取的主控制點，得到逼近折線的B樣條曲線。給出誤差控制方法，同時利用漸進迭代逼近方法的局部性，使所得逼近等距曲線的B樣條曲線達到預先給定的精度。實驗結果表明，該算法直觀簡潔，易于實現，可應用于任意平面參數曲線及函數曲線，并且其無需求解線性方程組，運算效率較高。

采樣點；切矢；特征點；等距線；B樣條曲線；漸進迭代逼近

1 概述

等距操作是計算機輔助幾何設計系統中一個重要的幾何運算，在CAD/CAM的很多領域中都有廣泛的應用，如數控加工、汽車車身設計等。但與此同時，等距計算又是一個十分困難的幾何運算，與基曲線相比，往往等距曲線的表達形式復雜，不利于實際應用。因此，對于等距曲線的研究是計算機輔助幾何設計的一個重要課題。在工程實際應用中，通常采用逼近方法，即用簡單且適用于CAD/CAM系統的曲線近似地表示等距曲線，如B樣條曲線、多項式曲線等。

等距曲線的逼近方法主要有以下4種類型：（1）基于控制頂點偏移的方法［1-3］，此類方法直接偏移基曲線的控制頂點，再用偏移得到的控制多邊形生成基曲線的等距逼近曲線。雖然其幾何直觀性較強，且不需要求解線性方程組，但曲線的表達式中需有控制頂點，故此類方法不能應用于任意表達形式的平面曲線，且大部分此類方法易造成最終得到的曲線控制頂點過多。另一方面，往往誤差控制不夠精確。（2）插值擬合的方法［4-6］。此類方法雖然對曲線的表達形式無特殊要求，但由于其擬合過程往往需要求解大量的線性方程組，因此造成計算上耗時較多。（3）包絡方法［7］。此類方法得到的逼近曲線次數過高。（4）其他方法［8-10］。文獻［8-9］的方法最終得到的逼近曲線次數過高。文獻［10-11］中提出的方法不能直接應用于NUBRS曲線。

從實際工程應用的角度來看，在求解平面曲線的等距曲線時，應綜合考慮以下6個方面的問題：（1）算法簡單；（2）精度高；（3）符合NURBS標準；（4）運算速度快；（5）適用任意曲線；（6）生成的控制頂點個數較少。本文針以上問題，結合漸進迭代逼近算法［11-12］（Progressive-iteration Approximation，PIA）提出一種新的平面等距曲線算法。

2 基于PIA的平面曲線等距線算法

本文要解決的問題是：給定一條平面參數曲線C（t）=（x（t），y（t）），t∈［t0，tn］和等距距離d，要求尋找一條逼近曲線C（t）的等距線Cd（t）的B樣條曲線。其實，對于函數曲線y=y（x），本文的提出的算法也是適用的，即可，下文稱曲線C（t）為基曲線。

本文算法的基本設計思想是：先離散化基曲線，得到逼近等距曲線的折線，將曲線與曲線的逼近問題轉化為曲線與折線的逼近問題，然后利用PIA算法逼近經離散化得到的折線。

本文算法的基本步驟是：利用基曲線C（t）上兩點的切矢轉角α的改變量來確定給定平面參數曲線的采樣點集｛oj，j=0，1，…，m｝，同時求得相應等距線上的采樣點集，并控制采樣誤差，其中，ε是預設的全局誤差閾值。將采樣點集｛pj，j=0，1，…，m｝依次連接，得到一條逼近等距線Cd（t）的折線Ld，即將曲線與曲線的逼近問題轉化為折線與曲線的逼近問題。對得到的采樣點集｛pj，j=0，1，…，m｝參數化，接著構造初始B樣條曲線：

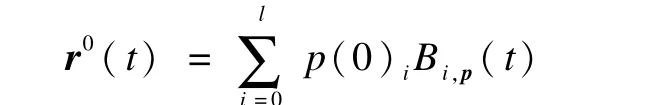
其中，｛p（0）i=pji，i=0，1，…，l｝，l＜m，pji是從采樣點集｛pj；j=0，1，…，m｝中選取的主控制點，作為B樣條曲線的初始控制頂點，Bi，p（t）是一組由節點向量｛tj，j=0，1，…，l+p+1｝確定的p次規范B樣條基函數。然后采用PIA算法通過迭代直到逼近誤差時停止迭代。最終得到的B樣條曲線插值所選的主控制點pji，并逼近由采樣點集｛pj，j=0，1，…，m｝連成的折線Ld。當逼近誤差或ea2，則需在不滿足誤差處插入節點向量，繼續迭代，直到滿足誤差為止。其中，ea=ea1+ea2，ea1為控制采樣點和逼近曲線的誤差，ea2為控制折線段與對應逼近曲線段的誤差。除了個別拐點處，該算法最后能保證等距逼近曲線（t）與等距曲線Cd（t）的全局誤差控制在預設的誤差閾值ε內。以上過程中的采樣過程、采樣點｛pj，j=0，1，…，m｝的參數化方法、主控制點p（0）i的選取方法、節點向量｛tj，j=0，1，…，l+p+1｝的構造方式、PIA迭代過程、逼近誤差ea的控制方法將分別在下文2.1節～2.6節中具體給出。

2.1 采樣算法及采樣點序列的參數化

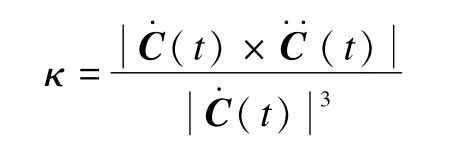
采樣的原則之一要保證2個采樣點之間的曲線段是凸曲線，故必須將曲線的拐點取作采樣點。基曲線的拐點與其等距曲線的拐點存在一一對應的關系。曲線上其切矢轉角符號發生改變的位置即為拐點位置。規定切矢轉角逆時針為正，順時針為負，方向是沿著參數值增大的方向轉動的。拐點如圖1所示，其中設點A為拐點。

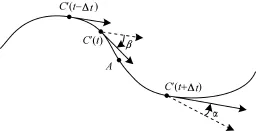
圖1 拐點取法示意圖

利用正弦函數的奇偶性，曲線C（t）與C（t+Δt）之間的切矢轉角α的計算公式如下：

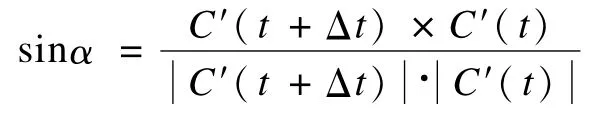
α=arcsin（sinα）

采樣的原則之二是保證相鄰兩采樣點之間的切矢轉角控制在預定的閾值范圍內，且等距線上相應的曲線段與其弦的距離在預定的誤差范圍內。目的是使得等距曲線上的取樣點能充分反映基曲線C（t）形狀特征，且控制由等距曲線上采樣點確定的折線在誤差范圍內全局逼近等距曲線，在此前提下盡可能地減少采樣點數量。下面給出采樣算法：

算法 SAMPLE

輸入 平面參數曲線C（t）=（x（t），y（t）），t∈［t0，tn］，預定的參數步長初值Δt，預定的角度閾值δ0，δ1，δ2（0＜δ0＜δ1＜δ2），預定的采樣誤差閾值ec

輸出 滿足采樣誤差的等距曲線Cd（t）采樣點序列集｛pj，j=0，1，…，m｝，取基曲線C（t）的首末點作為采樣點t←t0，tmp←Δt

運用本文的采樣算法，可以保證基曲線的特征點被完整保留，且曲線在曲率變化大的地方所取的樣點較密，在曲線曲率變化小的地方所取的樣點較疏，這樣就能達到用盡可能少但又足以保留曲線原有特征的一系列采樣點。再將這些采樣點集｛pj；j= 0，1，…，m｝順次連接起來，得到逼近等距線的折線Ld，并且Ld與等距曲線的全局誤差嚴格控制在預定的誤差范圍內。其中，采樣點的數量可以通過調整角度閾值δ1，δ2的取值來改變。

等距曲線Cd（t）上的采樣點序列｛pj，j=0，1，…，m｝的參數取為基曲線C（t）上對應采樣點的參數。設其參數序列為｛tj，j=0，1，…，m｝且滿足tj＜tj+1。

2.2 初始控制頂點的選取

等距曲線Cd（t）上的采樣點序列｛pj，j=0，1，…，m｝實際上顯示了等距線的基本形狀，而曲線C（t）的特征點與其等距線Cd（t）的特征點是一一對應的關系，如拐點。為了達到更好的逼近效果，這些特征點都應選取為主控制點，其余的主控制點按如下方法進行選取：

計算各個采樣點的離散曲率：

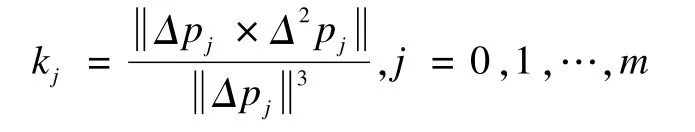
其中，Δpj和Δ2pj分別是采樣點pj的向前一階差分和二階差分，進而生成了離散的采樣點的曲率序列：

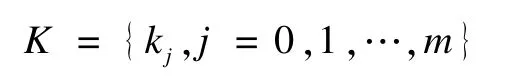
選取K=｛kj，j=0，1，…，m｝中局部曲率極大值點，即滿足kj-1＜kj，kj+1＜kj以及采樣點的首、末點。再與特征點一起構成采樣點序列｛pj，j=0，1，…，m｝的主控制點序列｛pj0，pj1，pj02，…，pjl｝，并將主控制點作為迭代的初始控制頂點，表示為：

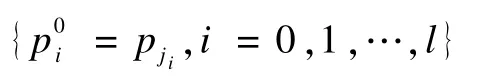
2.3 節點向量的構造

本文節點向量的構造采用平均的方法。初始B樣條曲線的初始控制頂點序列｛p（0）i=pji，i= 0，1，…，l｝的參數序列如下：

則p次（p+1階）初始B樣條曲線的節點向量序列構造如下：

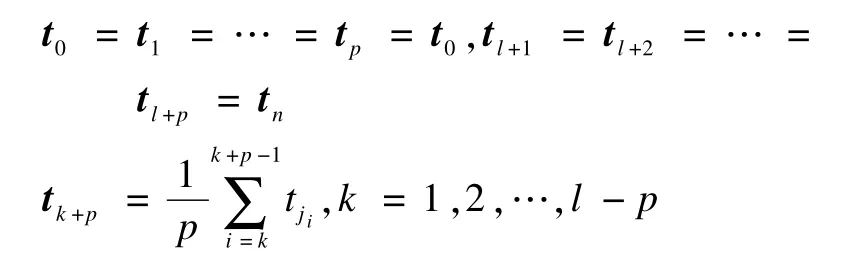
2.4 漸進迭代逼近插值采樣點

采用PIA算法插值這些主控制點｛pji，i=0，1，…，l｝，PIA算法是通過不斷調整控制頂點來最終插值所取的型值點集。將｛pji，i=0，1，…，l｝作為初始控制頂點，構造初始B樣條曲線r（0）（t）=（t），其中Bi，p（t），i=1，2，…，l是一組由節點向量｛tj，j=0，1，…，l+p+1｝定義的p次規范B樣條基函數，其組成一個標準全正基［14］。PIA算法迭代過程如下：第i個控制頂點的第一次調整差向量取為，把作為新的控制頂點，得到第一次迭代后的B樣條曲線：

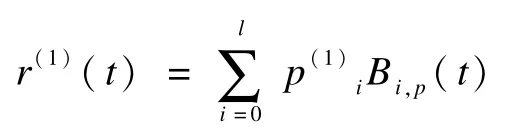
假設通過k次迭代后，產生曲線r（k）（t），則控制頂點的調整差向量為，控制頂點沿相應的調整差向量的方向移動，即，從而得到第k+1條曲線，即：

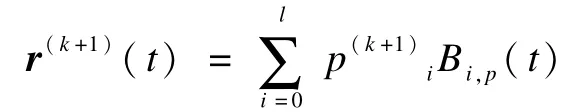
迭代過程如圖2所示。

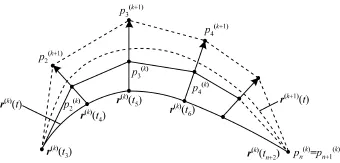
圖2 迭代非均勻B樣條曲線（r（k）（t）→r（k+1）（t））

2.5 逼近誤差控制

由于本文的思想是將基曲線離散化，得到逼近等距線的折線，將曲線與曲線的逼近問題轉化為曲線與折線的逼近問題，為保證在全局上控制曲線的逼近誤差，需考慮2個方面的逼近誤差：

（1）等距線Cd（t）與離散化折線Ld的全局誤差，在2.1節給出的采樣算法SAMPLE中，只要取采樣誤差閾值ec=ε/2，就可將等距線Cd（t）與折線Ld的全局誤差控制在范圍內。

（2）折線Ld與逼近的B樣條曲線的誤差，可分如下2個部分將該誤差控制在范圍內：

1）點與點的逼近誤差控制：利用PIA算法得到逼近等距曲線的B樣條曲線r（k）（t），t∈［t0，tn］插值于所選取的主控制點｛pji，i=0，1，…，l｝（這里設迭代插值產生的誤差忽略不計），而在每兩個主控制點pji-1，pjl之間還存在一些采樣點ps=pji-1，ps+1，ps+2，…，pe= pji，利用參數的對應關系，分別控制這些采樣點和逼近曲線上對應點的距離，當時，則說明該處已達到逼近的誤差精度，其中， k表示逼近曲線的迭代次數，ea1=ε/4，ε是預設的擬合誤差閾值。若，則說明該處未達到精度要求，需要在最大處插入節點，B樣條曲線節點插入可采用伯姆算法［15］，將該采樣點對應的參數值作為新節點插入到節點向量中，則相應的使B樣條曲線r（k）（t）增加一個控制頂點。當然，對多個誤差較大的點，可以同時對其進行插入節點，以提高算法效率。

2）B樣條曲線段與折線段的逼近誤差控制：計算采樣折線和逼近曲線的逼近程度來估計誤差。如圖3所示，pi和pi+1是等距線上的采樣點，對應的參數值分別為ti和ti+1，Qi和Qi+1是逼近等距曲線r（k）（t）上的參數對應點，r（k）′（ti）和r（k）′（ti+1）分別是Qi和Qi+1的切矢向量，設兩切矢向量交于點B，點B到線段QiQi+1的距離為h（k）i上面一步保證了點Qi和pi，Qi+1和pi+1的充分接近，就有線段QiQi+1和線段pipi+1充分接近，只要控制逼近曲線段r（k）（t），其中，t∈［ti，ti+1］充分接近線段QiQi+1即可，即保證。若不滿足該條件，則在最大誤差點處插入新的節點向量。直到滿足誤差精度。同樣，對多個誤差較大的處，可以同時對其進行插入節點，以提高算法效率。需要指出用高h控制誤差，對個別含有拐點的局部有可能不能完全控制。

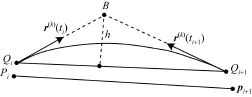
圖3 誤差控制示意圖

2.6 算法過程

基于PIA的平面等距曲線算法具體描述如下：

輸入 任意表達形式的平面參數曲線C（t），t∈［t0，tn］，等距距離d，精度ε，步長初值Δt，角度閾值δ0，δ1，δ2。

Step1 對平面參數曲線C（t）進行采樣操作。得到基曲線上的采樣點集

Step2 由等距公式Cd（t）=C（t）+d·N（t）計算相應等距曲線上的采樣點｛pj，j=0，1，…，m｝后，并將采樣點依次用線段連接起來，得到折線Ld。

Step3 選出等距曲線的特征點、首末點和局部曲率極大值點作為PIA算法的主控制點序列。

Step4 運用PIA算法插值主控制點序列，得到逼近等距曲線的B樣條曲線。

Step5 計算各個等距線上的采樣點和逼近曲線上對應點的距離，若不滿足精度要求，在處插入節點，轉Step4。

若Step5和Step6已達到，則終止。

注：本文算法的Step5和Step6可以同時插入多個節點。

3 實驗與結果分析

應用本文提出的針對任意平面曲線等距線逼近算法，本節給出3個實例，其分別從不同角度驗證本算法的有效性。其中，例1從誤差控制角度說明本文算法能有效控制逼近等距線的誤差；例2從最終得到的逼近曲線的控制頂點數量上和其他方法比較。例3是將該算法應用于一般的函數曲線。

例1 基曲線是一條五次Bezier曲線，其6個控制頂點為：

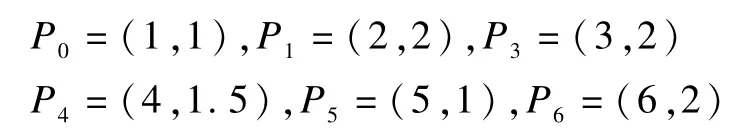
曲線的等距距離為d=1。先對基曲線進行采樣，取參數步長初值為Δt=0.02，角度閾值δ0=，分別選取38個采樣點中的8個，16個，20個主控制頂點，再用PIA算法生成等距曲線實驗結果如圖4所示。

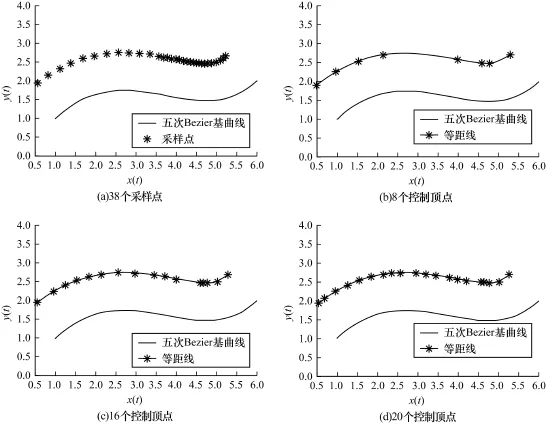
圖4 五次Bezier曲線采樣圖及其等距線的生成

圖4（a）是運用本文的采樣方法得到的38個采樣點。可以看出采樣結果在曲線走勢平緩處取點較少，反之取點較密，能充分反映基曲線的特征。圖4（b）中的逼近曲線達到預定誤差ε=10-2。圖4（c）中的逼近曲線達到預定誤差ε=10-3，圖4（d）中的逼近曲線達到預定誤差ε=10-4，可以看出隨著主控制頂點的增多，等距曲線的逼近程度越精確。

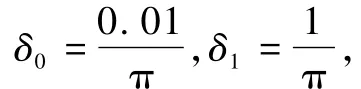
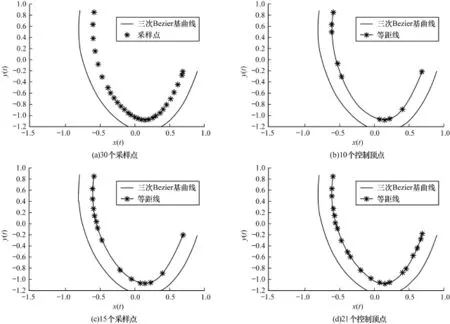
圖5 三次Bezier曲線采樣圖及其等距線的生成

圖5 （b）中的逼近曲線達到預給誤差ε=0.01，需要10個控制頂點。圖5（c）中的逼近曲線達到預給誤差ε=0.000 1，需要15個控制頂點，圖5（d）中的逼近曲線達到ε=0.000 01，需要21個控制頂點。以上都是在算法迭代20次情況下的結果。表1為在不同精度要求下應用不同方法求本例三次Bezier曲線等距線所需的控制頂點數的比較。

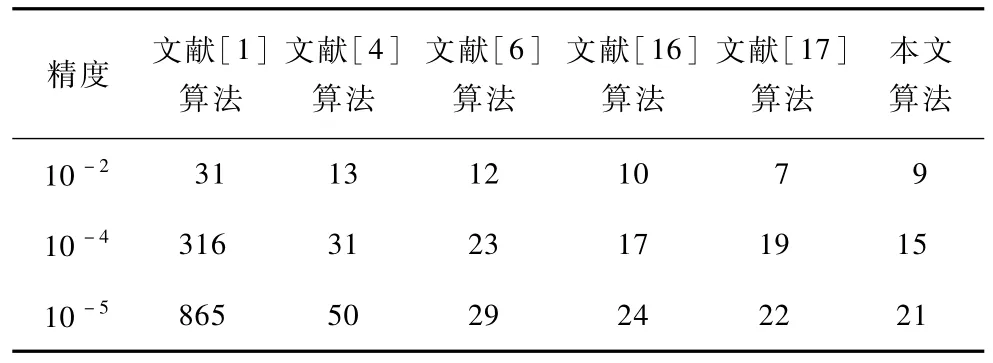
表1 逼近三次Bezier曲線等距線所需的控制頂點數

可以看出，在同樣的精度下，應用本文方法得到的控制頂點數較少。

例3 對于函數y=sin x+2cos x+x，x∈［-3.14，3.14］，可將其表示為參數曲線形式：

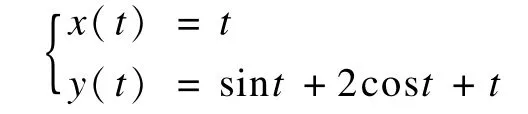
取曲線的等距距離d=1，采樣的參數步長初值，Δt=0.01，角度閾值δ0=0.01/π，δ1=1/π，δ2=1/π，運用本文算法所得到的等距曲線的B樣條逼近曲線的結果如圖6所示。

圖6（b）中的逼近曲線達到預給誤差ε=0.01，圖6（c）中的逼近曲線達到預給誤差ε=0.001，圖6（d）中的逼近曲線達到預給誤差ε=0.000 1，可以看出，隨著主控制頂點的增多，等距曲線的逼近程度越精確，誤差也越來越小。

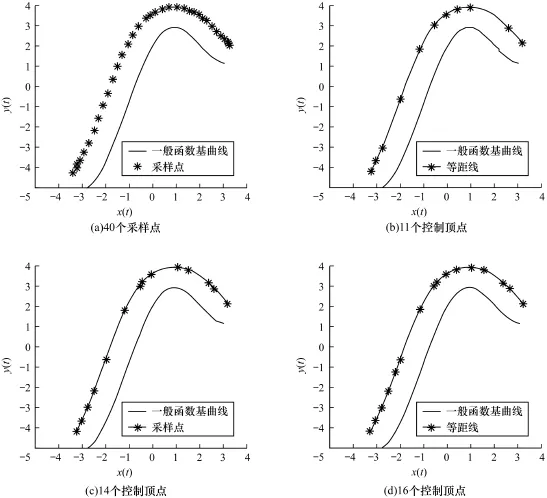
圖6 一般函數曲線采樣圖及其等距線的生成

4 結束語

本文算法在對等距曲線進行采樣的過程為自適應的，可保證在曲線曲率變化大的地方取較多的采樣點，在曲線曲率變化小的地方取較少的采樣點，這樣既保持了曲線的幾何性質，又減少了采樣點的數目，使算法更加快速。再應用漸進迭代方法插值所取的等距線上的主控制點，較之前應用最小二乘方法來逼近等距曲線，使算法效率得到提高。同時，由于漸進迭代算法具有局部性，因此在誤差大的地方可以局部地進行迭代。本文算法可應用于任意的平面參數曲線及函數曲線，能對逼近曲線進行全局誤差控制，且得到的B樣條逼近曲線的控制頂點數較少。下一步將在以下3個方面對本文算法進行改進：（1）在迭代過程中，考慮曲線的幾何特性以更好地控制等距逼近曲線的形狀。（2）進一步控制等距逼近曲線的誤差。（3）將本文算法推廣到曲面上。

［1］ Cobb B.Design of Sculptured Surfaces Using the B-spline Representation［D］.Salt Lake City，USA：Univesity of Utah，1984.

［2］ Coquillart S.Computing Offset of B-spline Curves［J］. Computing Aided Design，1987，19（6）：305-309.

［3］ 劉利剛，王國瑾.基于控制頂點偏移的等距曲線最優逼近［J］.軟件學報，2002，13（3）：398-403.

［4］ Hoschek J，Wissel N.Optimal Approximate Conversion of Spline Curves and Sp line Approximation of Offset Curves［J］.Computing Aided Design，1988，20（8）：475-483.

［5］ Piegl L A，Tiller W.Computing Offsets of NURBS Curves and Surfaces［J］.Computing Aided Design，1999，31（2）：147-156.

［6］ Khan M A，Chen Z C.Approximation of Planar O ffset Curves w ith Globally Bounded Error for B-spline NC Tool Paths［J］.International Journal of Production Research，2012，50（23）：6811-6825.

［7］ Shih J L，Chuang S H F.One-sided Offset Approximation of Freeform Curves for Interference-free NURBS Machining［J］.Computer Aided Design，2008，40（9）：931-937.

［8］ Zhao Hongyan，Wang Guojin.Error Analysis of Reparametrization Based Approaches for Curve Offsetting［J］. Computer Aided Design，2007，39（2）：142-148.

［9］ Zhao Hongyan，Wang Guojin.Offset Approximation Based on Reparameterizing the Path of a Moving Point A long the Base Circle［J］.Applied Mathematics：A Journal of Chinese Universities，2009，24（4）：431-442.

［10］ Ahn Y J，Hoffmann C，Kim Y S.Curvature Continuous Offset Approximation Based on Circle Approximation Using Quadratic Bezier Biarcs［J］.Computing Aided Design，2011，43（8）：1011-1017.

［11］ Lin Hongwei，Wang Guojin，Dong Chenshi.Constructing Iterative Non-uniform B-spline Curve and Surface to Fit Data Points［J］.Science in China Series F：Information Sciences，2004，47（3）：315-331.

［12］ Lin Hongwei，Zhang Zhiyu.An Extended Iterative Format for the Progressive-iteration Approximation［J］.Computers& Graphics，2011，35（5）：967-975.

［13］ 施法中.計算機輔助幾何設計與非均勻有理B樣條［M］.1版.北京：北京航空航天大學社，1994.

［14］ Lin Hongwei，Bao Hujun，Wang Guojin.Totally Positive Bases and Progressive Iteration Approximation［J］. Computings and Mathematics with Applications，2005，50（3/4）：575-586.

［15］ Boehm W.Inserting New Knots into B-spline Curves［J］. Computer Aid Design，1980，12（4）：199-201.

［16］ 嚴蘭蘭，宋來忠.正則Bezier曲線的等距線及其計算機實現［J］.計算機與數字工程，2006，34（8）：129-131.

［17］ Gu Jiulong，Jung Y.Approximation of Planar Offset Curves Using Quadratic Trigonometric Splines with Shape Parameter［J］.International Journal of Precision Engineering and Manufacturing，2013，14（11）：1881-1890.

編輯 金胡考

Algorithm for Offset of Planar Curve Based on Progressive-iteration Approximation

CHEN Qing，PAN Rijing
（College of Mathematics and Computing Science，Fujian Normal University，Fuzhou 350007，China）

Aiming at the existing problems in the computation of planar offset curves such as adaptability and error control，this paper proposes a new algorithm for generating the approximation offset of planar curves based on the Progressive-iteration Approximation（PIA）.This algorithm generates line segments approximating the exact offset curve by adaptive sampling on the progenitor curve with tangent vector angle that transfers the problem of approximating curve to that of curve approximating line segments.It reduces the number of sample point as possible at the premise of reflecting the shape feature of the progenitor curve.Then the algorithm selects the characteristic points on the offset curve as the dominant points，and interpolates the dominant points by using the PIA to generate a B-spline curve approximating the line segments. The B-spline curve can approximate the offset curve under the given error by utilizing the method of error control proposed in this paper and the locality of PIA.Experimental result shows that this algorithm is of intuition and easy implementation，which can be used directly for arbitrary planar parameter curve and function curve.It can increase the operating efficiency of the algorithm without solving a global linear equation system.

sampling point；tangent vector；characteristic point；offset；B-spline curve；Progressive-iteration Approximation（PIA）

陳 青，潘日晶.基于漸進迭代逼近的平面曲線等距線算法［J］.計算機工程，2015，41（11）：287-293，298.

英文引用格式：Chen Qing，Pan Rijing.Algorithm for Offset of Planar Curve Based on Progressive-iteration Approximation［J］.Computing Engineering，2015，41（11）：287-293，298.

1000-3428（2015）11-0287-07

A

TP391

10.3969/j.issn.1000-3428.2015.11.049

福建省自然科學基金資助項目（2010J01318）。

陳 青（1989-），女，碩士研究生，主研方向：圖像處理，計算幾何；潘日晶，教授。

2014-10-09

2014-11-06 E-m ail：554506497@qq.com