基于水平加權關聯規則挖掘算法的研究*

亓文娟

(武夷學院)

0 引言

經典的Apriori算法在進行關聯規則挖掘時存在數據庫中各項目具有著相似的出現頻率和相同的重要性兩個前提假設，但是現實世界數據庫中的數據并非如此，當數據庫中的各項目出現的頻率相差較大時，就會出現最小支持度閾值設置的兩難局面，為了解決這一問題，Liu［1］等學者提出了一種多支持度關聯規則挖掘MS-Apriori算法，但該算法認為各項目的重要性相同．文獻［2］提出了一種基于概率的多最小支持度關聯規則算法，有效挖掘出發生概率較低事件中的關聯規則，但存在著候選項集增多的缺點．文獻［3］提出了使用相關項目集中各項目最小支持度中的最大值來實現剪枝．為了區分各項目具有不同的重要性，需要根據各項目的重要性程度設置不同的權值，即加權關聯規則挖掘．加權關聯規則挖掘分為水平加權關聯規則挖掘、垂直加權關聯規則挖掘和混合加權關聯規則挖掘．水平加權關聯規則挖掘中項目的權值體現的是項目對決策的重要程度，垂直加權關聯規則挖掘中項目的權值隨著時間的變化而變化，混合加權關聯規則挖掘就是同時包含水平和垂直加權的關聯規則挖掘問題．本文深入分析了水平加權關聯規則典型算法MINWAL(O)的思想，指出了算法的不足及優化算法，旨在對加權關聯規則挖掘算法的擴展和改進奠定基礎．

1 加權關聯規則定義

假定事務數據庫D，項目的集合I={i1，i2，i3，…，in}，每一筆交易都是 I的子集，W={w1，w2，w3，…，wn}為I的權重集，其中項目ij對應的權重是wj，表示項目的ij重要程度，且0≤ wj≤1，j={1，2，…，n}．加權關聯規則形如 X?Y，其中X?I，Y?I，并且X∩Y=?．項集X在D中的支持度和置信度分別用 Support(X)，confidence(X)表示，根據傳統關聯規則可得到加權關聯規則的相關定義．

定義1 項集加權支持度為:

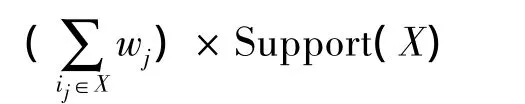
定義2 X?Y的加權支持度為:

定義3 X?Y的加權置信度為:

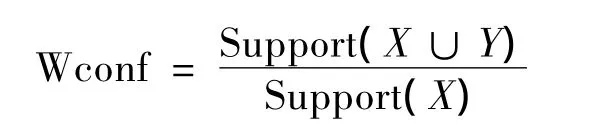
加權關聯規則就是挖掘同時滿足最小加權支持度閾值和最小加權置信度閾值的規則．

2 加權關聯規則MINWAL(O)算法

由于引入了權重的概念，區分了項目的不同重要程度，但也帶來了新的問題，即加權頻繁項集中不再符合普通關聯規則中頻繁項集所具有的反單調性，加權頻繁項集的子集有可能不是加權頻繁項集，因此必須采用新的解決方法．MINWAL(O)算法是由Cai C H等人在1998年提出的加權關聯規則挖掘算法［4］，該算法提出k-支持期望的概念，用于候選項集的剪枝操作，縮小了候選項集的規模．

2．1 k- 支持期望

假定事務數據庫D，其交易總數為n，對于任一k-項目集X，其支持數記為SC(X)，即事務數據庫D中包含X的交易個數．如果X為加權頻繁項集，則SC(X)應滿足下式:

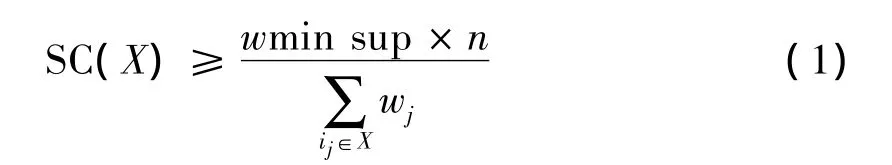
令I為所有項的集合，Y為一個q-項集(q＜k)，在剩余項目集合(I-Y)中，權值最大的前(k-q)個項為{wr1，wr2，…wr(k-q)}，則包含項集Y的任一k-項集的最大可能權值為

第1個和式是q-項集Y中各項目的權值之和，第2個和式是剩余的前k-q個項目的最大權值之和．由公式1和公式2可以推出:如果包含Y的k-項集是頻繁的，那么其最低支持數必須滿足下式:

稱B(Y，k)是項集Y的k-支持期望．為了保證Y的k-項集有可能是頻繁的，這里支持數采用向上取整的方式．在加權關聯規則挖掘中對候選頻繁項集進行剪枝的依據是B(Y，k)．

2．2MINWAL(O)算法

MINWAL(O)算法是基于Apriori算法的逐層搜索迭代思想，兩個算法都是通過頻繁項集來生成候選項集，但剪枝的依據不同，Apriori算法采用Apriori性質進行剪枝，而MINWAL(O)算法采用項集的k-支持期望進行剪枝，即保守估算任何可能成為其他加權頻繁項集子集的候選項，如果候選項的支持數不小于k-支持期望值就予以保留，否則刪除．MINWAL(O)算法的偽代碼如下:

MINWAL(O)算法的步驟如下:

MINWAL(O)算法:挖掘加權關聯規則．

輸入:(1)交易數據庫D，權重集W;

(2)最小加權支持度閾值wminsup和最小置信度閾值minconf;

輸出:加權關聯規則

begin

(1)size=Scan(D);//找出交易數據庫D中頻繁項集的最大可能長度

(2)L=?;

(3)for(i=1;i≤size;i++)//最大候選項集長度不大于size

(4)Ci=Li=?;

(5)for each transaction in D do

(6)(SC，C1)=Count(D，W);//累計1-項集的支持數，計算1-項集的k-支持期望，保留支持數不小于k-支持期望的1-項集為C1

(7)for(k=2;k≤size;k++){

(8)Ck=Join(Ck-1);//Ck是候選k-項集，Join(Ck-1)與Apriori算法的Gen函數類似

(9)Ck=Prune(Ck);//Prune(Ck)用于k-項集的剪枝操作

(10)(Ck，Lk)=Checking(Ck，D);//Lk是頻繁k-項集，遍歷交易數據庫D，更新Ck中所有候選項集的支持計數

(11)L=L∪Lk;}

(12)Rules．Set=Rules．Gen(L);// 與Apriori算法相同，根據L中的頻繁項集生成符合最小置信度閾值minconf的加權關聯規則

End

2．3 算法不足

MINWAL(O)算法雖然解決了加權關聯規則挖掘中加權頻繁項集的子集可以不是加權頻繁項集的問題，但是由于該算法是基于Apriori算法思想，也存在著不足之處:(1)頻繁掃描數據庫，生成大量候選項集，運行效率低，極大的影響了算法的性能;(2)利用求和權值法求得項目加權支持度，所以加權支持度可能大于1，這與支持度應小于1的實際相矛盾，有悖人們的思維方式;(3)挖掘得到加權頻繁項集并不是決策者感興趣的，加權頻繁項集可能包含多個權值較低的項目，因為權值之和較高，所以才被挖掘出來．

假設事務數據庫D，令wminsup=0．4，項目A，B，C，D，E 的權值分別為 0．2，0．3，0．3，0．6，0．7，如表1 所示．

表1 事務數據庫D

采用MINWAL(O)算法:

Wsup{E}=0．7 × 2/4=0．35;

Wsup{ABC}=(0．2+0．3+0．3)× 2/4=0．4;

可以看出，Wsup{E}的加權支持度小于wminsup，在項集{E}和{ABC}出現的頻繁程度相同時，挖掘到的加權頻繁項集包含{ABC}，而不包含{E}．

3 加權關聯規則的優化

針對MINWAL(O)算法的不足，很多學者對加權關聯規則進行深入研究，文獻［5］提出了一種基于時序和興趣度約束的加權關聯規則挖掘算法，該算法首先利用時序滑動函數對項目事務集中的數據集權值和發生概率進行估計，依據興趣度約束函數和剪枝定理對數據集簡化，然后根據支持度和k-支持期望進行加權頻繁事務集抽取，最后依據置信度進行加權關聯規則導出．實驗結果證明，該算法能夠快速有效地挖掘出符合用戶興趣度的關聯規則．文獻［6］針對事務數據庫長度不變，數據庫項目集發生變化時并且帶有權重時的關聯規則挖掘問題，提出了一種針對項目集增加的加權關聯規則更新算法，解決了增加項日集的加權關聯規則更新問題．文獻［7］針對加權關聯規則挖掘問題，提出基于關聯圖的加權頻繁項集生成算法及其剪枝策略．該算法掃描一次數據庫，通過關聯圖節點的度、是否有邊相連等作為判斷標準，減少生成頻繁項集的計算量，有效提高加權頻繁項集的生成效率．文獻［8］提出了基于時間聚類的加權關聯規則算法中權值設置方法，運用布爾向量的關系運算思想，設計了一種基于聚類和壓縮矩陣的加權關聯規則算法—CCMW算法．該算法通過聚類和對相同事務進行計數來壓縮矩陣以減小數據庫規模，并且只需掃描一次數據庫，無需產生候選項集直接生成加權頻繁項集．文獻［9］針對現有加權關聯規則模型中加權支持度定義和加權頻繁項集挖掘算法的不足，給出了挖掘加權頻繁項集的新算法——MWFI算法，該挖掘加權頻繁項集能保證:在項集出現的頻繁程度相同的情況下，如果權重小的項集是加權頻繁項集，權重大的項集一定是加權頻繁項集．但該算法存在，重復掃描數據庫，產生大量的候選項集的不足．

4 結束語

針對布爾關聯規則apriori算法在挖掘頻繁項集時，沒有充分考慮當數據庫中項目的出現頻率和重要程度相差很大這兩種情況，本文提出了加權關聯規則的概念，重點研究了水平加權關聯規則MINWAL(O)算法的基本思想，同時指出該算法的不足及優化算法，針對加權關聯規則的挖掘，有待進一步研究．

［1］ 王瑄．多最小支持度下的關聯規則研究［D］．長春理工大學，2008．

［2］ 田啟明，王麗珍，尹群．一種基于概率的多最小支持度挖掘算法［J］．計算機仿真，2006(7):115-118．

［3］ 何朝陽，趙劍鋒，江水．最大值控制的多最小支持度關聯規則挖掘算法［J］，2006(6):103-105．

［4］ 翟罡．Web數據挖掘中加權關聯規則算法的研究［D］．哈爾濱工程大學，2009．

［5］ 楊澤民．基于時序和興趣度約束的加權關聯規則挖掘算法研究［J］．計算機科學，2013(3):259-262．

［6］ 鄒長忠，傅清祥．一種新的加權關聯規則增量更新算法［J］．福州大學學報，2008(8):501-505．

［7］ 陳文．基于關聯圖的加權關聯規則挖掘算法［J］．計算機工程，2010(7):59-61．

［8］ 羅芳．基于聚類和壓縮矩陣的加權關聯規則算法的研究與應用［D］．華東師范大學，2010(10):24-37．

［9］ 王艷．一種加權關聯規則模型及挖掘算法研究［D］．河南大學，2007．