電學中的對稱美及其在高職電工基礎教學中的運用

徐 茜

（深圳職業技術學院，廣東 深圳 518055）

科學的本質是“真、善、美”，這種科學美，歷來為科學大師所推崇，法國數學家亨利·龐加萊（Jules Henri Poincaré，1854-1912）曾說：“一個名符其實的科學家，尤其是數學家，他在自己的工作中體驗到和藝術家一樣的印象。他的樂趣和藝術家的樂趣具有同樣的性質，是同樣偉大的東西。”[1]這種科學美在電工基礎理論中也有明顯表現，電工基礎理論所揭示的真理是真與美的統一。對稱美是電工基礎理論中常見的美學的特征，分析和探討電工基礎理論的對稱美學特征，并把它應用到高職教學中，對于改進教學，提高學生的學習興趣，拓寬思路改善思維方式有重要作用。

1 電工基礎理論中的對稱美

對稱（偶）性普遍存在于宇宙之中，在日常生活中處處都可見到對稱，潔白的雪花，彩色的蝴蝶，絢麗的花瓣等無不呈現出妙趣天成的對稱性。人們對于對稱性美的體驗，來自對于人體、動物、植物、山川、河流等外形美的觀感上，自然美的外觀表現是自然美的形式美。在中國的國粹文化中，對稱美具有獨特的地位，中國的建筑、繪畫、詩歌、楹聯、圖章、書法等，都閃耀著對稱美的光輝。對稱性的美學價值是一個神秘而有趣的現象。

電路是由電氣器件相互連接而構成的，具有傳輸電能、處理信號、測量、控制等功能。我們知道，分析集總參數電路，主要是基于兩類約束方程的求解，一類是元件約束方程，一類是電路結構約束方程（或拓撲約束方程）。元件約束是構成電路的每個元件上的電壓電流關系或稱伏安特性，如線性電阻元件，其元件約束滿足歐姆定律 u=Ri；結構約束是電路的連接關系確定后，各元件的電流之間或電壓之間受到的約束關系，表示這類約束關系的是基爾霍夫定律，它只與電路的拓撲結構有關，即對任意一個結點，與結點關聯的支路電流滿足基爾霍夫電流定律 ∑i=0，對任意回路，與回路關聯的各部分電壓滿足基爾霍夫電壓定律 ∑u=0。

在電路分析中，我們會發現一個有趣的現象，一些電路變量、元器件、電路結構乃至電路定律定理等會成對出現，其間會存在明顯的一一對應關系，這種特性稱為電路的對稱（偶）性。比如電壓u和電流i、電阻R和電導G、感抗和容抗、阻抗Z和導納Y、電感L與電容C、電壓源和電流源、VCCS和CCVS、VCVS和CCCS、網孔（回路）和結點、串聯和并聯、開路和短路、分壓和分流、基爾霍夫電流定律和電壓定律、戴維南定理和諾頓定理等等。顯然，線性電阻的伏安關系為u=Ri，線性電導的伏安關系為i=Gu，兩個關系式中，如果u和i、R和G互換，則兩個關系式可以互相轉換。同樣的，基爾霍夫電流定律表述為：對任意結點，有約束關系∑i=0，基爾霍夫電壓定律表述為：對任意回路（網孔），有約束關系 ∑u=0，如果結點和回路、i和 u互換，則兩個約束關系也可以互換。由于電路分析的兩類約束關系均存在這種互換性，可以推論，電路分析中，由這兩類約束關系推導得到的電路定理、電路分析方法等也存在這種互換性。上述具有這種一一對應關系，可以互換的元素稱為對偶元素。

電路中某些元素之間的關系（或方程），用他們的對偶元素對應地置換后，所得到的新關系（或方程）也一定成立，這個新關系（或方程）與原有的關系（或方程）互為對偶，這就是電路中有著美學特性的重要理論對偶原理[2]。

2 教學實踐中對稱美學的運用

高等職業技術院校各專業電工課程，并未將電路理論的對偶原理納入課程教學大綱，但這并不影響我們在教學過程中，很自然地引入哲學和美學范疇的“對偶（稱）”概念，它本身是一種自然的屬性，比如：遠近、高低、圓缺、胖瘦、大小、東西、男女、美丑、開關、增減、升降、上下、陰陽等等，對偶（稱）現象無處不在，而且因為形成對偶的兩個元素之間對比強烈，給大腦留下深刻印記，對偶在中國詩文中，常表現為對仗為大眾喜愛。

首先，通過引入對偶概念，加深對一些抽象電路概念的理解記憶。電路中，用足以反映其電磁特性的理想元件及其組合來模擬實際電路中的器件，即電路模型，其中，電阻R、電感L、電容C和電壓源模型的概念相對容易接受，而電流源是一個新的概念，因為生活中無從體驗，所以顯得更抽象。我們可以從相對熟悉的電感元件L和電容元件C引出對偶概念，L和C一個儲存磁場能，一個儲存電場能，磁場和電場是一對對偶量，L和C是一對對偶元件，進而提出，電壓源和電流源也存在對偶關系，電壓和電流也是對偶量。我們發現，對偶概念不僅反映在電路元件對偶（對偶元件）、電路結構對偶、電路特性對偶，也反映在電路定律和定理中，它是電路中普遍存在的現象。借助對偶概念，我們可以很自然地引入與電阻R對偶的一個電路元件電導G，以及歐姆定律對偶形式u=Ri和 i=Gu，發現基爾霍夫電壓定律和電流定律是一個對偶的結論∑i=0和∑u=0。

在電工教學中，我們一開始就自然引入對偶概念，不僅能加強對抽象概念的記憶，同時也能從宏觀上把握電路的規律性，讓初學者賞心悅目，感受到電學之美，激發學生學習興趣。電路中常見對偶元素見表1。

其次，在電路分析中不斷強化應用電學美學特性。如圖1所示，電阻的串、并聯電路，分析圖1（a）電路，得到，等效電阻 R=R1+R2，分壓公式：對于圖1（b）電路，只要分析說明它與圖1(a) 的對稱（偶）關系，電路結構對稱：并聯對串聯；電路變量對稱：電流對電壓；電路功能對稱：分流對分壓；電路元件的對稱：電導對電阻。并聯電路中的電阻常用電導參數表示，即G1=1/R1，G2=1/R2 ，這樣做的理由，僅僅是為了讓兩個電路完全對稱起來。于是得到圖1（b）電路等效電導G=G1+G2，分流公式：

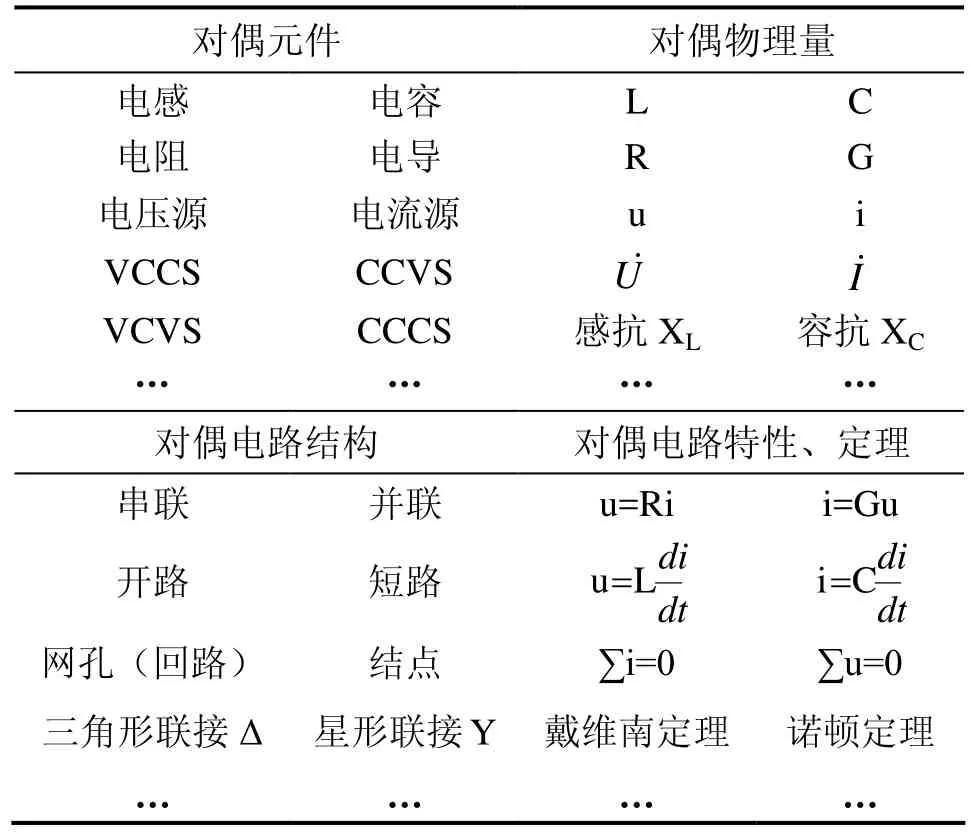
表1 電路常見對偶元素一覽

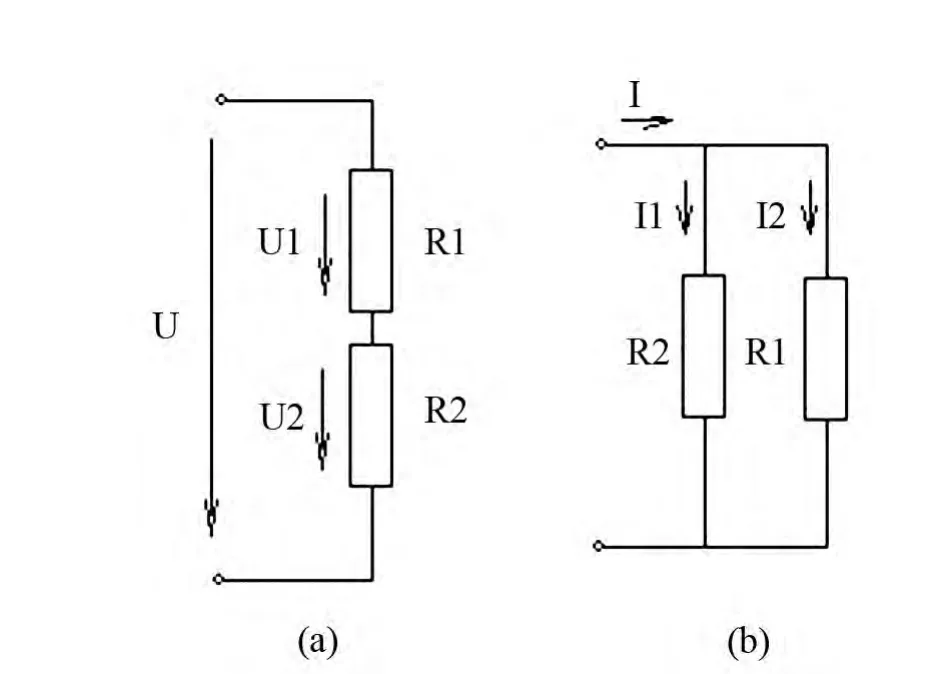
圖1 電阻串、并聯電路

這里，重點是對電路對稱（偶）特性的認識，方便記憶分壓分流公式，而且，這個結論可以推廣至n個電阻（導）串（并）聯的情況。

另外，借助電路對稱（偶）性特性，可以加深對電路抽象概念的理解。例如，電路模型中，有理想電壓源，自然就會有理想電流源。一個實際電源，可以用理想電壓源和一個電阻串聯來表示，與之對應，一個實際電源也可以用一個理想電流源和一個電導并聯來表示，這樣，可以自然而然地引出實際電源的兩種電源模型等等。在教學中，不斷地發現、認識、應用電路的對稱（偶）性、統一性等美學特性，達到事半功倍的效果。

3 幾點討論

3.1 從美學的觀點考察電學有利于思維方式的多樣化

現代科學是以概念為中心依靠邏輯推理建立起來的理論體系，電學也不例外，通過這套體系的嚴格邏輯性保證了電學的可靠性。但從美學的觀點考察電學，提供另外一個相對直觀的思維方式與觀察方法，有利于促進研究和教學的多樣化。

就電學中的對稱美來說，對偶原理的本質是電路中對應的對偶元素互換后，相應的數學方程（模型）是不變的，所以方程的解不變。它是電網絡理論中重要的電路定理。教學實踐中，我們更注重其在思維方法上的指導作用。通過對電路對偶元素的認識，運用對偶關系，使學生對基本概念、電路分析方法、電路定律、電路定理有更好的理解，記憶更牢固。在教學中，啟發學生善于比較分析，及時總結發現規律性的東西。

3.2 電工中的美學概念尚有許多可以深挖之處

除了對稱美的現象與概念之外，電學還有許多美學現象與概念可以進一步研究和探討。和諧統一性美就是一個例子。和諧是事物在矛盾對立的諸多因素相互作用下實現的統一。人的和諧感覺是與自然的和諧規律相統一的，它是一個合理的自然的運作規律。和諧統一是指由于相互之間恰到好處在整體上呈現出的協調，給人以統一、自洽、對應的美感。電學中的和諧美主要體現在電工理論形式與內容的統一、電路定律形式簡單、內涵豐富、和諧統一。形式的統一性，就是美的事物在外在形式所具有的相對獨立的審美特性。

直流電路中，元件約束方程的形式，即歐姆定律U=RI（直流電路中，電感L、電容C分別視為短路和開路）；電路拓撲約束方程的形式，即基爾霍夫電流定律和電壓定律：∑I=0（對任意結點），∑U=0（對任意回路）。電路分析實際上是一組線性代數方程的求解。

正弦交流穩態電路中，電感L、電容C不再被視為短路和開路，和電阻R類似，L、C在電路中對電流也有“阻礙”作用，很顯然這種“阻礙”作用的特性與電阻R是不一樣的。時域中，對電阻R，其元件約束方程依然是歐姆定律u=Ri，對電感L，其元件約束方程為對電容C，其元件約束方程為電路拓撲約束方程依然是基爾霍夫定律 ∑i=0 （對結點）和∑u=0 （對回路），因此，正弦穩態電路分析實際上是常系數n階微分（積分）方程的求解（其特解）。微分方程的求解比線性代數方程組求解繁雜得多，為此，正弦穩態電路的分析常用相量法。相量法本質上是一種數學變換，通過變換，建立時域的正弦量與相量域的相量的對應關系。我們發現，應用相量法，正弦穩態電路兩類約束方程在形式上與直流電路是相似的：元件約束方程I&Z （對電阻Z=R，對電感Z=jwL，對電容稱為相量形式歐姆定律；同樣地，電路拓撲約束方程：∑I=0（對結點），∑0=（對回路），稱為相量形式基爾霍夫定律。兩類約束方程形式上的高度統一性，使得用相量法分析正弦穩態電路時，直流電路中的所有分析方法、電路定理等可以直接引用。這充分展現了電工理論簡潔、和諧統一之美。

3.3 從美學視角認識、學習電工理論知識是提高學生學習興趣有效方法

愛因斯坦說過：“興趣是最好的老師。教育應當使所提供的東西讓學生作為一種寶貴的禮物來接受，而不是作為一種艱苦的任務要他去負擔。”電工基礎課程的學習，對高職學生來講普遍存在一定的困難：概念抽象、理論性強。因此，從探討電工理論中的美學概念入手，為學生提供一種相對直觀的思維方式和方法，善于引導學生去發現、認識電路的對稱（偶）性、統一性，把它和生活中的審美結合起來，對于激發學生的學習興趣提高學習效果極為有效。從第一堂課開始，就引入電路對稱（偶）性概念，目的不是介紹一個電路定理，而是一個認知的過程，從元件、結構、現象、功能等的對稱（偶）性，進而到電路公式、電路定理的對稱性，學習的過程變得有趣、生動，公式和定理不再只是死記硬背。

[1] 徐本治．數學中的美學方法[M]．大連：大連理工大學出版社，2008．

[2] 邱關源．電路（第四版）[M]．北京：高等教育出版社，1999．

[3] 楊紅，徐茜．電工及電氣測量技術[M]．北京：機械工業出版社，2013．