改進的Dijkstra最短路徑算法在GIS-T中的研究與實現

戴文博 殷招偉 錢俊彥

（桂林電子科技大學計算機科學與工程學院，廣西 桂林 541004）

改進的Dijkstra最短路徑算法在GIS-T中的研究與實現

戴文博 殷招偉 錢俊彥

（桂林電子科技大學計算機科學與工程學院，廣西 桂林 541004）

Dijkstra最短路徑算法廣泛應用于交通運輸和網絡優化等領域，但是在實際應用的過程中仍存在一些不足。文章針對道路擁擠、交叉路口等待和單行道限行等方面提出了一種改進的基于時間最短的最短路徑算法。傳統的最短路徑算法中圖的頂點是抽象的，不含權重的，改進的算法中圖的頂點是有權值的，用來表示道路交叉口的等待時間。通過編程實現該算法，實驗結果表明，道路擁擠、交叉口等待和單行道限行對交通路徑選擇有很大影響。因此，改進的算法求得的最短時間路徑更加符合實際，具有一定的應用價值。

Dijkstra最短路徑算法；最短時間路徑；交通運輸；網絡優化

隨著城市化進程的加快，城市交通網絡的規模也在不斷擴大，交通設施日益發達，但這也使城市交通變得異常復雜。這也就促使了交通地理信息系統（GIS-T，Geographic Information System for Transportation）的應用日益廣泛。GIS-T是地理信息系統（GIS）[1]在勘測設計、道路規劃和管理等領域中的具體應用，它充分考慮了現有的交通網絡的特征，過濾掉 GIS多余的功能，減少冗余，更加高效、快捷的管理和規劃交通[2]。為了能夠使得資源和時間得以充分利用，必須考慮到車輛路徑規劃。車輛路徑規劃問題一般指的是對一系列的起點和終點，調用一定的車輛，組織選擇一條或多條適當的行車路線，使車輛有序的通過它們，在滿足指定的約束條件下（如距離最短、時間最短、費用最低等），爭取實現如車輛行駛里程最短、運行時間最短、運費最低等目標[3]。而 GIS-T的重點之一就是路徑規劃分析，因此，交通路徑規劃問題必然成為 GIS-T的研究熱點之一，而路徑的選擇取決于多種因素，較常見的有三種：車輛行駛距離、車輛所需費用和車輛行駛時間。在具體應用中，有些司機愿意選擇距離最短，有些司機愿意選擇費用最少，有些司機愿意選擇最短出行時間。

無論采用何種標準，最優路徑規劃最終都可以歸結為在特定道路網中尋找具有最小代價的最短路徑問題[4]。

因此，就需要合理的規劃交通路線以滿足人們需求。本文就如何使得行駛時間最短進行了討論。

在研究問題的過程中，可以將實際的交通網絡模型化成網絡圖，根據圖論的相關知識，交通網絡中的兩點之間的最短路徑就可以用圖中頂點之間的最短路徑表示。圖的最短路徑問題由很多國內外學者進行了深入的研究，提出了許多種最短路徑算法，其中Dijkstra提出了一個按路徑長度遞增的次序產生的最短路徑算法是目前已知的理論上最完善、應用最多的算法[5]。這些算法解決了兩點之間的最短路徑問題，但是有時需要的并不是兩點之間的最短距離而是追求時間和速度上的需求。那么我們就需要考慮將圖中的邊或弧的權值由行駛時間替換路段距離，對于道路擁擠和交叉路口紅綠燈等待時間也是需要考慮的因素，而對于某些單向限行的道路可能在一些地圖軟件中搜索到的最短路徑是不太實用的。

1 相關基礎知識

1.1 Dijkstra最短路徑算法

Dijkstra最短路徑算法是由荷蘭計算機科學教授迪杰斯特（E.W.Dijkstra）在1959年提出的，它被公認為是最經典的算法之一，也是解決最短路徑問題的基礎算法。它可以從某點到網絡中其余各頂點的路徑長度依次遞增的順序產生最短路徑，適應于所有弧或邊的權值為非負的圖。

Dijkstra算法的基本思想可以簡單的描述為：從起始頂點出發，找到從起始頂點到其余各頂點中第1、第2……第n短的路徑，這樣就獲得了從起始頂點到其余各頂點的最短路徑。如果要獲得從起始頂點到某個頂點的最短距離，則直到找到這個頂點的最短路徑就停止，不再繼續查找[6]。

1.2 算法理論基礎

單源最短路徑問題，即根據最短路徑的最優子結構性質，在圖中求出從給定的頂點到其他任意頂點的最短路徑。最優子結構的性質可以描述為：如果D(i, j)= {Vi…Vk…Vs…Vj}是從頂點i到j的最短路徑，k和s分別是這條最短路徑上的中間結點，那么D(k,s)必定是從頂點k到頂點s的最短路徑距離[7]，下面證明該性質的正確性。

假設D(i, j)={Vi…Vk…Vs…Vj}是從頂點i到j的最短路徑，D(k, s)不是從k到s的最短路徑距離。那么則有D(i, j) =D(i, k)+D(k, s)+D(s, j)，而D(k, s)不是最短的，故存在另一條從k 到s比D(k, s)更短的D’(k, s),那么D’(i, j)=D(i, k) +D’(k, s)+D(s, j) ,由于D’(k, s)＜ D(k, s),那么D’(i, j)＜ D(i, j)，這與D(i, j)是從i到j的最短距離相矛盾，從而該性質得證。

根據以上性質可知，如果在一條從 i到 j的最短路徑{Vi…Vk，Vj}，那么{Vi…Vk，Vj}，Vk是Vj的前驅結點，那么{Vi…Vk}也必然是從i到k的最短路徑，據此，Dijkstra提出的一個按路徑長度遞增的次序產生的最短路徑算法，如對于起點V0，首先選擇與其直接相連的頂點中長度最短的頂點Vi，那么可得V0到Vj的最短距離Distance[j]= min{Distance[j] , Distance[j]+matrix[i][j]}[8]。

翻轉課堂教學可以解決上述問題，以學為本建設優質的在線開放課程，開啟課程資源共享與應用模式，學生課下先學習老師提供的基礎知識，如果有問題就可以記錄下來，在課堂上由老師答疑或同學討論來解決。翻轉課堂通過把傳統的課堂學習和線上學習的優勢結合在一起，實現線上線下混合式教學，可以更好地加強面對面的互動，培養學生團結協作的能力，提高教學效果，開啟學生深度學習，滿足不同學生對象的學習需求[5]。

2 最短時間路徑算法

2.1 道路網的模型建立

對于前面提到道路擁堵而導致的時延，我們可以通過交通部門發布的實時數據來獲取該道路的實時平均速度，從而根據路長，求得該段線路的車輛行駛時間。將交通網絡轉換為網絡圖，那么該段路線車輛行駛時間即為網絡圖中兩頂點的弧的權值；對于交叉口紅綠燈延誤的時間，可以轉換為圖中頂點的權值，而在傳統的最短路徑算法中，圖的頂點是沒有權重的，只起到標識的作用，在算法中是不起作用的；對于單行線路段，可以動態的改變有向圖中弧的方向。由此，可以得到該道路網的模型如圖1。

圖1 道路網模型圖

圖1中，圓圈分別表示各個道路網的頂點，圓圈旁的Vi （i=0，1，…，5）為各頂點的標識符，圓圈中的數字表示各個交叉口的等待時間，弧段上的數字表示車輛路段行駛時間，當圖中某兩個頂點分別表示起點和終點，延誤時間不需計入。

2.2 改進的算法思想

由于在傳統的最短路徑算法中，圖的頂點是沒有權值的，因此，我們需要在定義圖的結構過程中額外增加一個vertex[MaxVexNum]數組來存儲圖中所有頂點的權值來解決交叉口等待時間[9]。然后根據上面的性質假設存在G=＜V,E＞，源頂點V0，Distance[i]記錄的是V0到Vi最短時間，path[i]記錄的是V0到Vi前驅的一條最短路徑，matrix是用來表示帶權有向圖的鄰接矩陣，matrix[i][j]表示弧＜Vi, Vj＞上的權值。若＜Vi, Vj＞不存在，則將matrix[i][j]置為∞或者一個相對較大的值。求解V0到其余各頂點的最短時間路徑，由于在改進的算法中，圖的頂點是有權重的，因此，在計算源點到各頂點的最短時間時需要將圖的頂點計算進去。基本思想如下：

（1）初始化頂點集S={V0}和T=V-S，集合S中存放已經找到的最短時間路徑的頂點而集合T中存放余下的頂點。

（2）不斷的從集合T中選擇頂點V0到頂點Vu的最短時間路徑長度即Distance[u]最小的頂點Vu加入到集合S中。

（3）更新V0到集合T中剩下的頂點的最短時間路徑長度，Distance[j]=min{Distance[j],Distance[j]+matrix[i] [j]+vertex[i]},這是本算法的核心部分。

（4）重復上面的(2)、(3)兩步驟，直到S=V結束。

2.3 算法求解過程針對圖1，算法的求解過程如下表1所示，V0到各個頂點的最短時間路徑分別是：V0-＞V2，最短時間為10；V0-＞V4，最短時間為30；V0-＞V2-＞V3，最短時間為80；V0-＞V2-＞V3-＞V5，最短時間為95。

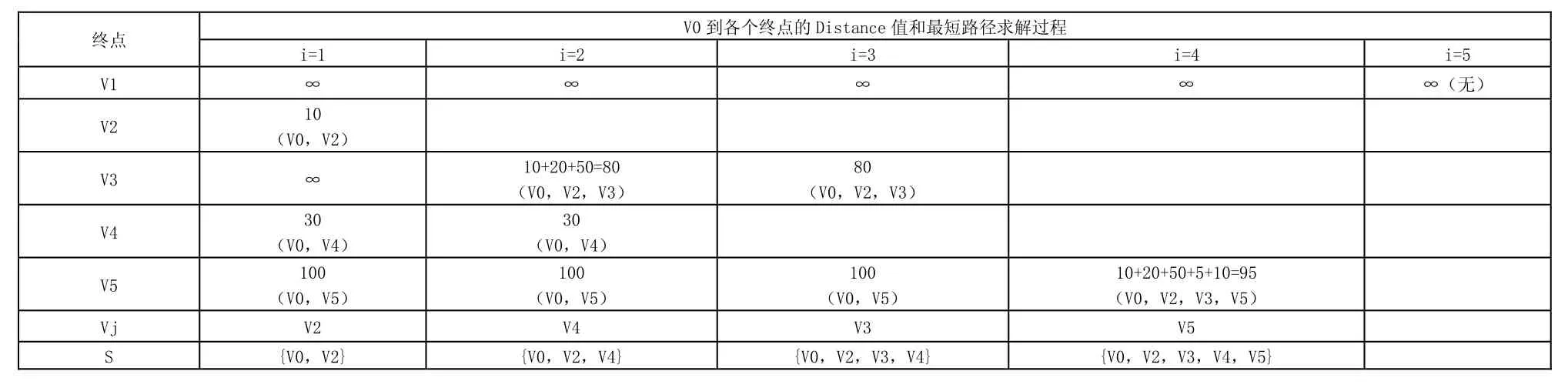
表1 V0到各個終點的Distance值和最短路徑求解過程

2.4 算法部分代碼

在傳統的最短路徑算法中，圖頂點沒有權重，因此，頂點在算法中不起作用，但是在改進的算法中，圖的頂點是有權重的，因此，在圖結構定義的時候，添加一個 vertex[Max Vexnum]數組來表示頂點的權重。

3 實驗結果與分析

3.1 實驗結果

本文的仿真實驗環境：處理器為Inter(R) Core(TM)2 Duo CPU/2.93GHz,內存為2.00GB的PC機，根據上述算法，編寫的程序代碼在VS2010集成環境下運行結果圖2和圖3。

3.2 實驗結果分析

本文是用車輛行駛的時間來替換路段長度表示路徑上的權重，由此還是轉換為求解網絡最優路線問題。由表1和圖3，可以算法的求解過程和程序執行過程是一致的。由圖2和圖3可知，在傳統的算法中，V0到V3的最短路徑為V0-＞V4-＞V3，計算權值為50，V0到V5的最短路徑為V0-＞V4-＞V3-＞V5，計算權值為60；而在改進的算法中，V0到V3的最短路徑為V0-＞V2-＞V3，計算權值為 80，V0到 V5的最短路徑為V0-＞V2-＞V3-＞V5，計算權值為95。這就充分說明了圖中頂點有無權值，對最短路徑有較大的影響，即交叉口的交通紅路燈等待時間對最短時間路徑的選擇有很大的影響，對于單行線，只是改變有向圖中的弧的方向，那么只需在搜索最短時間路徑前更新鄰接矩陣matrix[i][j]中對應的值。因此改進的算法更貼近實際。而對于算法執行的時間，由于結點個數少，兩個算法的執行時間都在納秒級別。改進后的算法時間復雜度O(n2)與傳統最短路徑算法的復雜度一致。

圖2 傳統最短路徑算法的執行結果

圖3 改進的算法的執行結果

4 結語

本文主要討論了Dijkstra最短路徑算法并在其基礎上提出了基于時間的最短時間路徑算法，傳統的算法網絡圖中頂點是沒有權重的，而改進的算法增加了頂點的權重來表示交叉口紅綠燈等待時間，該算法主要解決了道路擁擠、交叉路口紅綠燈等待和單行線路段限制的路徑規劃問題，并通過算法編程實驗證明，使得搜索到的最短時間的路徑更加的符合實際，更能滿足人們的需求，具有較大的應用價值。

[1] 劉學軍,徐鵬.交通地理信息系統[M].北京:科學出版社, 2006.

[2] Miller H J, Shaw S L. Geographic information systems for transportation: principles and applications[M]. Oxford University Press,2001.

[3] 孫麗君,胡祥培,王錚.車輛路徑規劃問題及其求解方法研究進展[J].系統工程,2006,(11):31-37.

[4] 林清巖.智能交通中車輛最優路徑規劃策略研究[D]. 吉林大學,2013.

[5] 嚴蔚敏,吳偉民.數據結構(C語言版)[M].北京:清華大學出版社,1997.

[6] Chuan-xiang REN,Xin-gang HAO,Ying-rui Wang. Research on the Optimization and Simulation of the Shortest PathBased on Algorithm of Dijkstra[J]. Journal of Measurement Science and Instrumentation, 2010.

[7] 胡運權.運籌學教程(第 3版)[M].北京:清華大學出版社,2007.

[8] 秦鋒,湯亞玲.數據結構:C語言版[M].北京:清華大學出版社,2011.

[9] 陳悅.基于行程時間組合預測模型的動態路徑誘導系統研究[D].華南理工大學,2012.

Research and implementation of the improved Dijkstra shortest path algorithm in GIS-T

Dijkstra shortest path algorithm(DSPA) is widely used in fields of communication and transportation and network optimization, etc. But there are still some shortcomings in the process of practical application. We propose an improved SPA based on the minimum duration which is directing at the aspects such as congested roads, the intersection waiting and one-way street restrictions. The vertex of diagram in tradition SPA is abstract and does not contain the weight, while does and is used to represent the intersections waiting time in improved algorithm.We program to implement it and the results show that the above three aspects mentioned has a great influence on choice of the transportation route. Therefore, the shortest time path wh3ich is gained by the improved algorithm is more in line with the actual and the improved algorithm has a certain application value.

Dijkstra shortest path algorithm; the shortest time path; communication and transportation; network optimization

TP312

A

1008-1151(2015)02-0001-03

2015-01-12

戴文博，男，桂林電子科技大學計算機科學與工程學院碩士，研究方向為GIS-T及數據庫應用；殷招偉，桂林電子科技大學計算機科學與工程學院碩士；錢俊彥，桂林電子科技大學計算機科學與工程學院博士。