多冷源空調系統節能優化調度算法初探

陳眾勵 許維勝

（同濟大學 上海 201804）

1 引言

城市綜合體建筑規模龐大（單體建筑面積可達數十萬乃至百萬平方米，建筑高度可達數百米），內部功能復雜（通常包括商業、餐飲、影視、賓館和辦公等不同業態），建筑能耗巨大，其中采暖與空調系統能耗約占一半，故節能潛力相當可觀。

為滿足城市綜合體建筑中各種不同業態的空調需求，通常設置多種冷源系統（或裝置）。常見的冷源系統（裝置）包括：

（1）冷水機組，由電力驅動空氣壓縮機使冷媒降溫；

（2）溴化鋰機組，由天然氣、人工煤氣等燃氣燃燒產生的熱量使冷媒汽化，并間接制冷；

（3）熱電冷三聯供系統，以燃油發電機驅動發電機組產生電能，同時將發電機的余熱用于冷媒的汽化并間接制冷；

（4）冰蓄冷裝置，在公共電網用電低谷時段（同時也是電價的低谷時段）用電力驅動冷凍機組進行制冰作業，并在此日通過融冰達到制冷目的；

（5）地源熱泵系統，利用深層地表的恒溫特性（12 ℃左右），將部分空調系統的冷水管網深埋地下，使其與地表土壤進行熱交換，從而對室內空氣進行冷卻。

（6）自然風空調系統，當室外溫度顯著低于室內溫度時，利用室外冷卻塔將空調系統的冷水進行自然冷卻，從而達到令室內降溫的目的。

上述各種制冷裝置所消耗的能源種類不盡相同，制冷效率不同，制冷成本也不同。通過對這些不同種類的冷源、在不同電價區間（取決于一天內的不同時間段）內的優化調度，達到綜合能耗最低或運行成本最低，是多冷源空調系統節能優化調度算法的核心研究目標。

2 城市綜合體建筑多冷源空調系統節能優化調度問題的描述

2.1 系統調度的目標

城市綜合體建筑多冷源空調系統需要在確保室內環境舒適性的前提下，同時實現下列目標：

（1）耗電最少。

（2）基于峰谷電價制度的電費最少，其中，任意一天內的的電價P（t）為階躍函數。

（3）耗燃氣最少。

（4）燃氣費用最少，設定任意一天內的燃氣價格為常數。

（5）耗柴油最少。

（6）柴油費用最少，設定任意一天內的柴油價格為常數。

為了電費最少，就應減少電價高峰時段（午后和初夜）的耗電，在夜間電價低谷時段（子夜和凌晨）應合理的多用電能制冰蓄冷。而這一目標（電費最少）與耗電最少的目標并不完全一致。

為了實現單純的耗電最少的目標，就應盡可能地不用或少用耗電的冷水機組、冰蓄冷系統（該系統利用夜間低電價時段進行制冰蓄冷，故需消耗大量電能，雖然省錢但不節能）、地源熱泵系統（該系統工作時需開啟循環水泵等用電設備）以及自然風空調系統（該系統工作時需要運行冷卻塔風機、水泵等耗電設備），同時用足或多用以天然氣為主要能源的溴化鋰空調系統和以柴油為主要能源的熱、電、冷三聯供系統。

為了實現單純的耗天然氣最少的目標，顯然就應盡可能地不用或少用溴化鋰機組，同時用足或多用耗電的冷水機組、冰蓄冷系統、自然風空調系統，以及耗油的三聯供系統。

類似地，為了實現單純的耗柴油最少的目標，則應盡可能地不用或少用耗油的三聯供系統，同時用足或多用耗電和耗天然氣的空調設備。

由此可見，目標1）和目標2）的最優值是不同步的（即存在利益沖突）；目標 3）與目標 4)的最優值是同步的（即利益一致）；目標5）和目標6）的最優值是同步的；目標1）、目標3）、目標5）的最優值之間互不同步；目標2）、目標4）、目標6）之間的最優值互不同步。

因此，城市綜合體建筑多冷源空調系統的節能優化調度問題是一組相互排斥的目標集。

2.2 系統調度問題的約束條件

為了滿足城市綜合體建筑室內環境的舒適性要求，多冷源空調系統的節能優化調度問題應同時滿足下列約束條件：

（1）各子系統的制冷量之和應等于建筑物所需總冷量C（t），其中C（t）為時變函數。

（2）冷水機組的制冷量不大于其額定值，即，C1（t）≤C1（常數）;

（3）溴化鋰機組的制冷量不大于其額定值，即，C2（t）≤C2（常數）；

（4）三聯供系統的制冷量不大于其額定值，即，C3（t）≤C3（常數）；

（5）冰蓄冷系統的制冷量不大于其額定值，即，C4（t）≤C4（常數）；

（6）地源熱泵系統的制冷量不大于其額定值，C5（t）≤C5（常數）

（7）自然風系統的制冷量不大于其額定值，即，C6（t）≤C6（常數，設計最大值）。

上述約束條件構成了多冷源空調系統的約束集。

綜上所述，城市綜合體建筑多冷源空調系統的節能優化調度問題中，需要滿足約束條件的前提下，同時處理多個相互矛盾、相互排斥的目標，故可以歸結為約束型的多目標優化調度問題（Multiobjective Optimization Problem，MOP，也稱MOPSO）。

3 多目標優化問題的基本算法

3.1 多目標優化問題的一般描述

多目標優化問題一般由 n個決策變量、k個目標函數和m個約束條件組成，且三者之間存在某種函數關系。[1-2]

一般多目標優化問題的數學描述如下：[3]

X表示決策向量組成的集合，稱為決策空間（decision space）或參數空間（parameter space）。決策向量（decision vector）x=（x1，x2，…，xn）由n個決策變量組成。

Y表示目標向量形成的目標空間（objective space）或判據空間（criteria space）。

目標函數F（x）將決策向量x映射成一個k維向量y=（y1，y2，…，yk），該k維向量稱為目標向量（objective vector）或判據向量（criteria vector），記作F：Ω→∧。

約束條件gi（x）≤0決定決策向量可行的取值范圍。

由于目標函數和約束條件可能是線性或非線性、凸或凹或不凸不凹、可微或不可微、連續或不連續、單峰或多峰的，因此目標空間和決策空間可能是凸或非凸、緊或非緊、連通或分離的[4]。顯然，問題的規模由決策變量、約束條件和目標數量共同決定，在MOPOS優化過程中，各個目標往往是相互沖突的，達到各自極值的時機無法同步，因此并不存在一個在約束條件內能使所有目標函數達到全局最優的解。為此，必須首先找出最優解（Pareto Dominance，也稱非劣最優解）的可行解集和最優解前端，并最終搜尋出最優解。

3.2 非劣最優解的評價方法

對多目標問題最優解的評價方法實質上是一種建立在集合論基礎上的優劣性評價體系。所謂非劣最優解是指在目標函數的解集中，對其中一個或多個子目標函數的進一步優化不會使其它子目標函數的解失效（即超出規定的范圍），也即在多目標優化中對某些子目標的優化不會影響到其它子目標的優化而容許的整個多目標體系的解。

為建立解的優劣性評價體系，在最優解中引入了支配向量（Dominate Vector）的概念，其定義為：

基于對支配關系的判斷，并可篩選出非劣最優解（Pareto Dominance）、全局最優解（Globally Optimal Solution）和Pareto最優解集：

（1）若x*是搜索空間（決策變量）中的一點，當且僅當在搜索空間的可行域內不存在x使得fn(x)≤fn(x*)(n =1 ,2,… ,N)成立時，稱 f(x*)為非劣最優解。

（2）對于多目標優化問題的f(x)，當且僅當在搜索空間中的任意x，f(x*)≤f(x)都成立時，則稱 f(x*)為全局最優解。

（3）由所有非優劣最優解組成的集合即為多目標優化的Pareto最優解集。

Pareto最優解集對應的所有目標函數值所形成的空間便是所謂的Pareto前端（Leading End）。

解決了解的評價問題后，面對各種不同的多目標問題算法，建立對算法性能的評價體系顯然是有意義的。

3.3 多目標優化算法的性能評價

多目標優化算法的評級體系主要包括下列指標：

（1）逼近性（Generational Distance，GD），反映了算法所獲得的非劣最優解與Pareto前端的距離。其定義為

式中disti表示第i個非劣解與Pareto前端的距離。

（2）均勻性（Spacing，SP），反映了非劣解在Pareto前端上的分布范圍，其定義為：

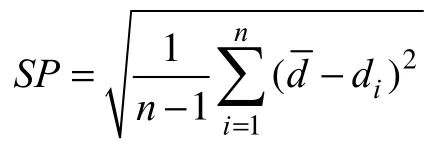
式中，di是兩非劣解間的距離，是其平均值。

（3）寬廣性（Extention，EX），反映了非劣最優解的分布范圍。

（4）最優解差錯率（Error Ratio，ER）用來描述在算法獲得的非劣最優解中不屬于Pareto前端的解所占的比例。

（5）收斂性度量值γ，用來衡量一組已知的Pareto最優解集的收斂范圍。

收斂性度量的評價方法為在多目標優化問題的Pareto前端均勻地取若干點構成Pareto前端基點系，計算由算法獲得的Pareto最優解與基點之間的距離的最小值，所有這些最小值的平均值就是收斂性度量值γ。

（6）多樣性度量值Δ，用來衡量Pareto前端的分布均勻度，其定義為：

式中，di是兩非劣解間的距離，是其平均值，df是Pareto前端中極值點的距離，dl是邊界點的距離。

其中，非劣解的收斂性和多樣性對 MOP算法評價的核心指標。[5]

4 基于粒子群優化算法（PSO）求解多目標問題的基本思路

在Reynolds提出的BOID鳥群模型[6]中，每只鳥類個體的行為只和它相鄰個體的行為有關，并遵循“避免碰撞（Collision Avoidance）、速度一致（Velocity Matching）和趨向中心（Flock Centering）”的基本原則。在初始狀態下，鳥群中的個體在隨機位置上往隨機方向自主飛行，但在“避免碰撞、速度一致和趨向中心”三原則的驅使下，最終所有個體通過自組織（Self-organization）趨于一致并匯聚于食物所在位置。

受上述 BOID鳥群模型的啟發，Kennedy和Eberhart共同提出了粒子群優化算法（PSO）[7]。在這一算法模型中，每個粒子的自身狀態都由位置向量和速度向量來描述，這兩個參數分別代表問題的可行解和它（粒子）在搜索空間中的運動方向。粒子通過迭代搜索，不斷學習它當前的群體最優解和個體最優解，最終達到全局最優。粒子的位置和速度的迭代方程是PSO算法的核心，在連續空間中其基本算法（適用于單個目標的情形）描述如下：

設在一個N維的目標搜索空間中，有M個粒子組成一個群落，將第i個粒子表示為一個N維的向量：

pin=（pi1，pi2，…，piN），其中，i=1，2，…，M。

即第i個粒子在N維搜索空間中的位置是pin。每一個粒子都是潛在的解，將pin代入一個目標函數就可以計算出其適應值，根據適應值的大小衡量pin的優劣。第i個粒子的飛行速度也是一個N維的向量，記為vin=（vi1，vi2，…，viN），速度決定粒子在搜索空間單位迭代次數的位移。

記第 i個粒子群當前搜索到的最優位置為：ppbestn=（ppbest1，ppbest2，…，ppbestN）,整個粒子群當前搜索到的最優位置為pgbestn=（pgbest1，pgbest2，…，pgbestN），粒子按照下列公式來迭代更新其速度和位置:

其中，i=1，2，...M；

n=1，2，...N；

ω為權重慣量，其主要作用是避免早熟而陷于局部最優。比較簡單的處理方式是將其初始取值為0.9，然后在迭代過程中線性地遞減到 0.4。也有文獻建議按函數關系ω=ωmax?（ωmax?ωmin）IC/ICmax進行迭代計算（Iterative Computations），式中，ICmax為預定的最大迭代次數；

c1，c2為加速系數（Acceleration Coefficients，也稱學習因子），c1=0，則忽略了個體經驗，c2=0則忽略了群體經驗，通常兩者均不可取。一些文獻建議在0～4之間的取值，而種群規模適中的工程應用中一般取2.0；

r1，和r2為介于[0，1]之間的隨機數；

V（i+1）n∈[?vmax，vmax]，vmax為常數（可根據經驗設定），vmax的每一維通常取相應維的取值范圍的10%～20%[7]。

上述計算公式中，等式右邊的第一部分為慣性分量，是遺傳（或繼承）粒子上一次運動結果的矢量；第二部分為個體認知量，是反映向個體歷史最優位置運動的量；第三部分為群體認知量，是反映粒子向全局最優位置運動的量。

迭代中止條件可選為粒子群搜索到的最優化位置滿足適應閾值或達到預定的最大迭代次數。由于pgbestn是整個粒子群的最優值，因此上述 PSO算法也稱為全局PSO算法。全局 PSO算法收斂速度較快，但有可能陷入局部最優。

如果把第 i個粒子的鄰居粒子搜索到的最優位置作為pgbestn，則上述方法可稱為局部 PSO算法。與全局PSO算法相比，該收斂速度較慢，但相對而言不易陷入局部最優。

PSO基本算法的流程圖[8]如下：

流程圖中單目標 PSO算法的基本思路可以描述為：

→初始化粒子位置（一般都是隨機生成均勻分布）

→計算適應度值（一般是目標函數值-優化的對象）

→初始化歷史最優 ppbestn為其本身和找出全局最優Pgbestn

→根據速度和位置公式分別進行速度和位置的更新

→重新計算適應度

→根據適應度更新歷史最優 Ppbestn和全局最優Pgbestn

→收斂或者達到最大迭代次數則結束運算

其中，在解決實際工程問題時，種群規模、權重慣量、加速系數等參數需要在對工藝條件進行深入研究的基礎上才能合理地確定。對于城市綜合體建筑多冷源空調系統而言，系統所需的總冷量具有時變、隨機和離散（各個空調冷源系統的輸出可能是連續變量，也可能是離散變量，取決于控制方式。）等特性，而且多冷源空調系統也諸多客觀條件的限制（約束條件）。

在PSO算法中引入群體智能（Swarm Intelligence SI）的思想[9-10]，將使算法具有收斂快、精度高且容易實現等優點，這對于解決諸如多冷源空調系統節能優化調度之類組合優化問題頗具優越性。

5 約束型多目標調度問題的智能微粒群優化算法及其改進

用 PSO的基本算法來解決多目標優化問題將面對兩個困難。

首先需要解決Ppbest的選擇問題。對于單目標優化問題而言，選擇Ppbest時，只需作簡單比較就可以選擇出哪個是當前最優。但是對于多目標問題而言，兩個粒子之間的簡單對比，并不能判斷出哪個更優。因為很可能某個粒子比一部分粒子好，但又比另一部分粒子差，或者說不存在絕對好的粒子。

其次需要解決Pgbest的選擇問題。對于單目標問題而言，在種群中只有一個最優的個體（Pgbest）。而對于多目標問題而言，最優的個體可能有多個（Pgbest族）。但是PSO基本算法的規則體系中，只允許選擇一個粒子作為最優的個體（引領者）。

對于第一個問題，通過仔細分析PSO算法的機理，我們就能發現其實比較容易處理：雖然我們不能通過簡單比較篩選出歷史最優，但可以隨機選擇其中一個作為歷史最優，讓運算規則來找到實際最優。

對于第二個問題，Carlos A等人于2004年提出了在最優集（存檔，Archive）中根據擁擠程度選擇引領者的策略，其主要規則是盡量選擇處于不擁擠位置的粒子，比如使用網格法（Grid）[11]進行選擇。

MOPSO算法在選擇引領者和對存檔（Pareto當時最優集）進行更新時，可以應用自適應網格法，其基本策略為：[12]

根據網格劃分，假設每個網格中粒子數為g個，i代表第幾個網格。該網格中的粒子被選擇的概率為pi=1/gi，即粒子越擁擠，則選擇的概率越低。這是為了確保那些未知區域也能得到探索。

在種群更新完成之后，存檔工作通過三輪篩選來完成：

→根據支配關系進行第一輪篩選，將劣解去除，剩下的加入到存檔中；

→在存檔中根據支配關系進行第二輪篩選，將劣解去除，并計算存檔粒子在網格中的位置；

→若存檔數量超過了存檔閥值，則根據自適應網格進行篩選，直至達到閥值限額為止。然后，重新進行網格劃分。

顯然，改進后的智能微粒群優化算法更適用于解決多目標優化問題。

6 約束型多目標優化調度算法的工程化過程中應注意的問題

基于智能微粒群優化算法的約束型多目標問題求解過程具有較好的收斂性，故具有較好的應用前景。但應注意的是，多冷源空調系統的運行條件具有明顯的動態特性。因為大型建筑中，空調系統總制冷量C值受諸多因素影響，其因素包括：

（1）室外熱輻射F（t），具有隨機性，但可通過檢測設備獲得實時數據并輸入調度系統中。

（2）室內人數P（t），具有隨機性，但可通過檢測設備獲得實時數據并輸入調度系統中；建筑物內人員的作息表，可預訂規則并輸入調度系統中。

（3）建筑照明系統的空調負荷經由智能控制系統的調節而呈現出動態。

（4）配電系統中，電力變壓器的熱損耗約占其自身功率的2%，并隨著其負載率的變化而變化。

因此，建筑物的總制冷量為時變函數，且具有明顯的隨機、離散分布特性，這些因素都是工程化過程中需要重點研究和解決的問題。

7 結論

本文從大型建筑物中多冷源空調系統的節能優化調度問題出發，探討了以智能粒子群算法為基礎的約束型多目標優化問題的算法及其改進方向。此類算法只有在經歷仿真實驗、現場試運行及最終定型等工程化蛻變過程后才有可能在實際工程中得到廣泛應用。

[1] Van Veldhuizen DA.Multiobjective evolutionary algorithms:classifications,analyses,and new innovations(PHD thesis).Ohio:Air Force Institute of Technology,Wright-Patterson AFB,1999.

[2] 崔遜學.基于多目標優化的進化算法研究[D].安徽:中國科技大學,2001.

[3] 郭文忠,陳國龍.離散粒子群優化算法及其應用[M].北京:清華大學出版社,2012.

[4] 于堷杰,周根貴譯.遺傳算法與工程優化.北京:清華大學出版社,2003.76-108.

[5] 章勇高,高彥麗,劉煥等.三相不平衡時的PWM整流器鎖相環設計[J].華東交通大學學報.2011,28(5):14-17.

[6] 肖曉偉,肖迪,林錦國.多目標優化問題的研究概述[J].計算機應用研究,2011,28(3):805-808.

[7] Kennedy J,EberhartRC.Partcls swarm optimization.[C].Proceedings of IEEE international Conference on Neural Networks.Piscataway,NJ:IEEE Service Center,1995.1942-1948.

[8] 張軍,詹志輝,等,計算智能[M].北京：清華大學出版社,2009.

[9] 吳啟迪,汪鐳.智能微粒群算法研究及其應用[M].南京：江蘇教育出版社,2005.

[10] 高尚,楊靜宇.群智能算法及其應用[M].北京：中國水利水電出版社,2006.

[11] Carlos A.Coello,GregorioToscanoPulido,Maximino Salazar Lechuga.Handling multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Compution,2004,8(3):

[12] Joshua D.Knowles,Approximating the non dominated front using the Pareto Archived Evolution strategy,UK,Evolutionary Computation,8(2),149-172,2000.