基于非線性輸出頻率響應(yīng)函數(shù)的多裂紋轉(zhuǎn)子故障診斷方法研究
李志農(nóng),杜宜光,肖堯先
(南昌航空大學(xué)航空制造工程學(xué)院,江西南昌330063)
基于非線性輸出頻率響應(yīng)函數(shù)的多裂紋轉(zhuǎn)子故障診斷方法研究
李志農(nóng),杜宜光,肖堯先
(南昌航空大學(xué)航空制造工程學(xué)院,江西南昌330063)
相對(duì)單條轉(zhuǎn)子裂紋的故障診斷,多條裂紋的故障診斷更復(fù)雜,也更困難。以兩條裂紋為例,將非線性輸出頻率響應(yīng)函數(shù)(NOFRF)引入到具有兩條裂紋轉(zhuǎn)子系統(tǒng)的故障診斷中,提出了一種基于NOFRF的多裂紋轉(zhuǎn)子故障診斷新方法,并且對(duì)比分析了兩條裂紋不同夾角、不同裂紋深度下NOFRF值的變化情況。實(shí)驗(yàn)結(jié)果表明,NOFRF值對(duì)裂紋故障具有很高的敏感性,根據(jù)NOFRF值的變化情況,不僅能反映轉(zhuǎn)子系統(tǒng)裂紋是否存在,還能反映兩條裂紋之間的夾角、裂紋深度的變化情況。因此,利用NOFRF值,可以有效地監(jiān)測(cè)轉(zhuǎn)子系統(tǒng)中多條裂紋故障。
動(dòng)力機(jī)械工程;非線性輸出頻率響應(yīng)函數(shù);裂紋轉(zhuǎn)子;故障診斷;裂紋夾角;裂紋深度
0 引言
在與轉(zhuǎn)子有關(guān)的各種故障中,裂紋故障具有難于發(fā)現(xiàn)、診斷困難,后果嚴(yán)重的故障特征。20世紀(jì)70年代據(jù)加利福尼亞電力研究所統(tǒng)計(jì)[1],透平發(fā)電機(jī)組發(fā)生的23起故障中,有8起是低壓轉(zhuǎn)子軸和發(fā)電機(jī)軸橫向裂紋引起,占故障總數(shù)的35%.同時(shí),國(guó)內(nèi)時(shí)常也有轉(zhuǎn)子裂紋事件的報(bào)道,姚孟電廠在維修時(shí)發(fā)現(xiàn)了一部電機(jī)的主軸上有3條裂紋,其中最深的一條裂紋深度竟達(dá)到直徑的2/3.渦噴六發(fā)動(dòng)機(jī)在使用的過(guò)程中,也曾多次發(fā)生渦輪軸近盤根部處產(chǎn)生裂紋以至折斷的嚴(yán)重事故。因而,能否及時(shí)發(fā)現(xiàn)裂紋故障,對(duì)防止發(fā)生災(zāi)難性轉(zhuǎn)子斷裂事故,減少非計(jì)劃停機(jī)及提高經(jīng)濟(jì)效益具有重大意義。目前,針對(duì)具有單條裂紋故障診斷的研究取得了很大進(jìn)展[1-6]。相比單裂紋故障,產(chǎn)生多裂紋故障的轉(zhuǎn)子系統(tǒng)非線性特性更強(qiáng),危險(xiǎn)性更大,后果也將更為嚴(yán)重。因此,對(duì)于轉(zhuǎn)子系統(tǒng)上多裂紋故障的診斷也越來(lái)越被重視。印度學(xué)者Darpe等[7]采用集中質(zhì)量法建立轉(zhuǎn)子模型,研究了含雙呼吸型裂紋轉(zhuǎn)子的動(dòng)力學(xué)特性。于濤等[8]從斷裂力學(xué)理論出發(fā),討論了雙裂紋轉(zhuǎn)子系統(tǒng)非線性動(dòng)力學(xué)特性,為多裂紋轉(zhuǎn)子系統(tǒng)故障識(shí)別提供了理論依據(jù)。文獻(xiàn)[9]采用較為簡(jiǎn)單的余弦型裂紋呼吸模型,利用有限元方法,分析了含兩條裂紋的轉(zhuǎn)子系統(tǒng)動(dòng)力學(xué)特性。Chasalevris[10]建立了轉(zhuǎn)子裂紋的柔度矩陣,利用小波分析的方法,研究了彎矩作用下梁上雙直裂紋的檢測(cè)方法。
以上裂紋故障的檢測(cè)方法根據(jù)對(duì)系統(tǒng)輸入輸出信號(hào)處理方式的不同,可以分為兩大類:一類是利用傳感器獲得的信號(hào)來(lái)分析,另一類是考慮系統(tǒng)模型來(lái)診斷。二者的區(qū)別在于前者只考慮了系統(tǒng)的輸出信號(hào),而后者不僅考慮了系統(tǒng)的輸出信號(hào),而且還考慮了系統(tǒng)的激勵(lì)。很顯然,前者只對(duì)輸入穩(wěn)定的系統(tǒng)才有效。后者克服了前者存在的不足,因?yàn)檩敵鲂盘?hào)的變化有可能是系統(tǒng)的激勵(lì)引起,而系統(tǒng)的固有特性并沒有改變,這時(shí)僅根據(jù)輸出信號(hào)的變化來(lái)診斷勢(shì)必會(huì)造成誤判。
故此,基于非線性模型的故障診斷方法得到很快發(fā)展。其中,英國(guó)Shiefld大學(xué)Lang等[11-14]從Volterra級(jí)數(shù)出發(fā),提出了非線性輸出頻率響應(yīng)函數(shù)(NOFRF)的概念,并推導(dǎo)出NOFRF的辨識(shí)方法。該方法不僅能清晰準(zhǔn)確地反映出系統(tǒng)輸出頻譜與非線性參數(shù)之間的關(guān)系,而且各階次的函數(shù)都是一維的,從而可方便地用圖表分析來(lái)解釋。Peng等[15-18]在NOFRF理論也做了一些有意義的探索,并將NOFRF的概念應(yīng)用于振動(dòng)信號(hào)分析和結(jié)構(gòu)的裂紋故障檢測(cè)中。李志農(nóng)博士領(lǐng)導(dǎo)的課題組利用NOFRF方法對(duì)轉(zhuǎn)子裂紋故障進(jìn)行了有效地辨識(shí),得出了轉(zhuǎn)子上含有橫向裂紋、斜裂紋的NOFRF特
性[19-20]。
然而,現(xiàn)有的基于NOFRF的轉(zhuǎn)子裂紋故障診斷方法主要是針對(duì)轉(zhuǎn)軸上具有單條裂紋展開的,對(duì)于采用NOFRF對(duì)轉(zhuǎn)子上具有多條裂紋的轉(zhuǎn)子系統(tǒng)特性研究少有涉及。基于此,本文引入NOFRF理論并對(duì)轉(zhuǎn)子系統(tǒng)上含有兩條橫向裂紋展開辨識(shí),提出了基于NOFRF的兩條裂紋轉(zhuǎn)子系統(tǒng)的故障診斷方法。通過(guò)實(shí)驗(yàn)研究,分析了不同裂紋夾角、不同裂紋深度時(shí)轉(zhuǎn)子系統(tǒng)各階NOFRF值的變化特征,為具有多條裂紋的轉(zhuǎn)子系統(tǒng)故障診斷提供了一種新的有效方法。
1 非線性輸出頻率響應(yīng)函數(shù)理論及其辨識(shí)算法
NOFRF是在Volterra級(jí)數(shù)模型的基礎(chǔ)上提出來(lái)的,可用于研究一大類的非線性系統(tǒng)的動(dòng)態(tài)特征。假設(shè)u(t)和y(t)分別為非線性系統(tǒng)的輸入和輸出,則該系統(tǒng)的Volterra級(jí)數(shù)模型可以表示為
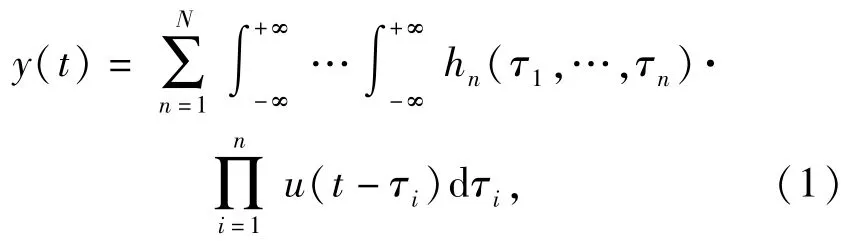
式中:hn(τ1,…,τn)為非線性系統(tǒng)的第n階Volterra核,n=1,2,……,N;t為時(shí)間;τ為時(shí)延。相應(yīng)地,非線性系統(tǒng)的輸出在頻域內(nèi)的表達(dá)式為
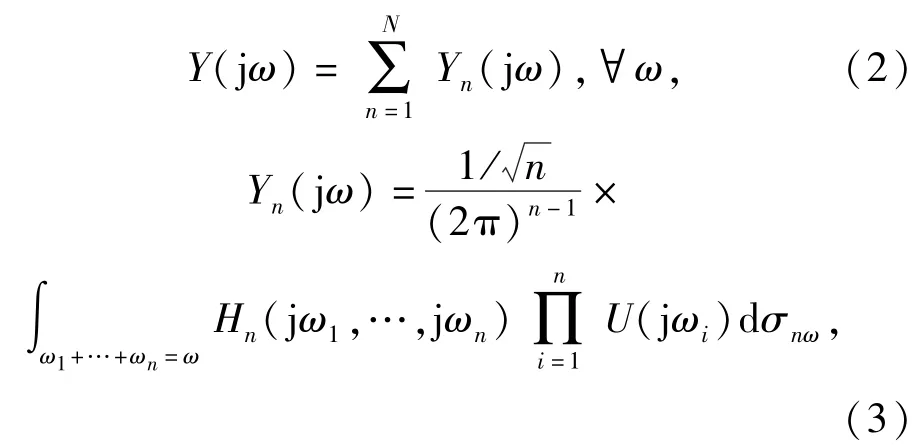
式中:Yn(jω)表示第n階非線性系統(tǒng)的輸出頻率響應(yīng);Y(jω)是該系統(tǒng)輸出y(t)的傅里葉變換;U(jω)是該系統(tǒng)輸入u(t)的傅里葉變換;Hn(jω1,…,jωn)表示非線性系統(tǒng)的第n階廣義頻率響應(yīng)函數(shù)。
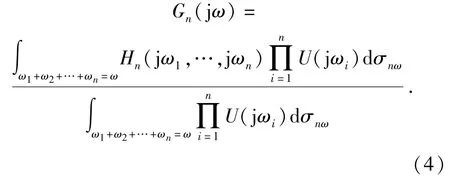
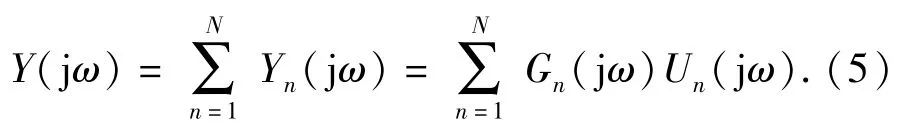
對(duì)照傳統(tǒng)的線性系統(tǒng)輸出頻率響應(yīng)函數(shù),如圖1所示,發(fā)現(xiàn)(5)式所描述的NOFRF表達(dá)形式和線性系統(tǒng)的輸出頻率響應(yīng)函數(shù)相似,NOFRF是線性系統(tǒng)輸出頻率響應(yīng)函數(shù)Y(jω)=G1(jω)U(jω)的自然延拓。類似地,(5)式所描述的非線性系統(tǒng)輸入輸出頻譜關(guān)系可以用圖2來(lái)描述。
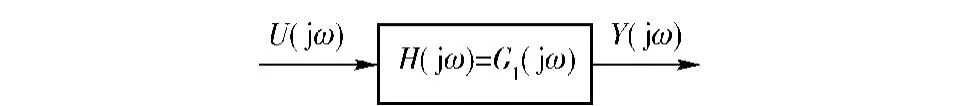
圖1 線性輸入輸出頻率響應(yīng)關(guān)系Fig.1 The frequency response between output and input of a linear system
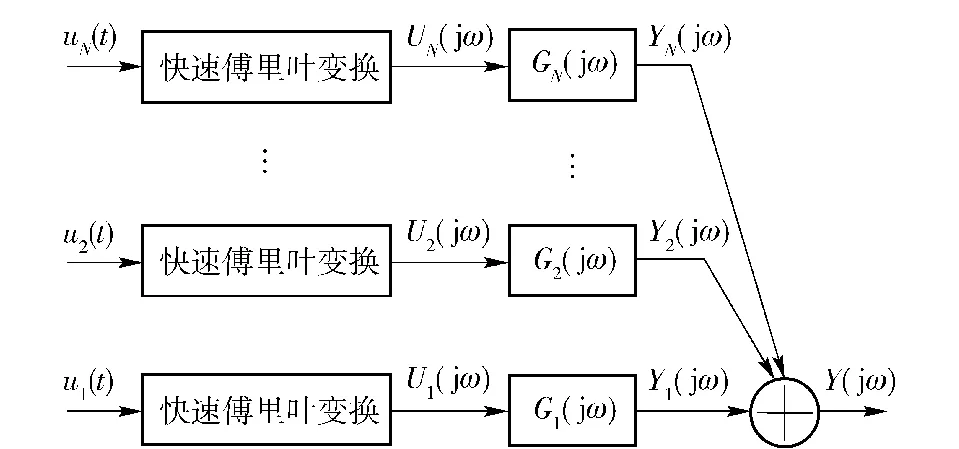
圖2 非線性系統(tǒng)輸入輸出頻率響應(yīng)關(guān)系Fig.2 The frequency response between output and input of a nonlinear system
NOFRF可用于反映系統(tǒng)的振動(dòng)特性,與廣義頻率響應(yīng)函數(shù)(GERF)相比,其各階核值也可由采集的輸入輸出信號(hào)確定,但是,NOFRF有一個(gè)更加重要的特征,即其各階次的函數(shù)都是一維的,可以較容易地根據(jù)系統(tǒng)的輸入、輸出信號(hào)估計(jì)得到,避免產(chǎn)生維數(shù)災(zāi)難。
由(5)式可知,非線性系統(tǒng)的輸入輸出函數(shù)關(guān)系可改寫成
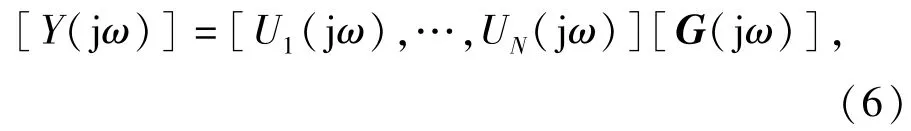
式中:G(jω)=[G1(jω),…,GN(jω)]T.令u(t)= αu*(t),α為一個(gè)不為0的常數(shù),u*(t)為非線性系統(tǒng)的輸入信號(hào),則
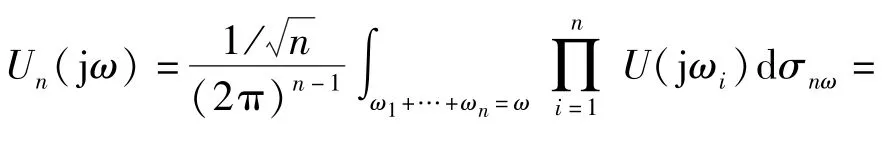
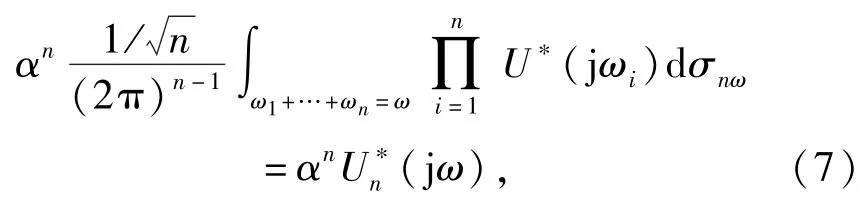
式中:U*(jω)是u*(t)的傅里葉變換,且
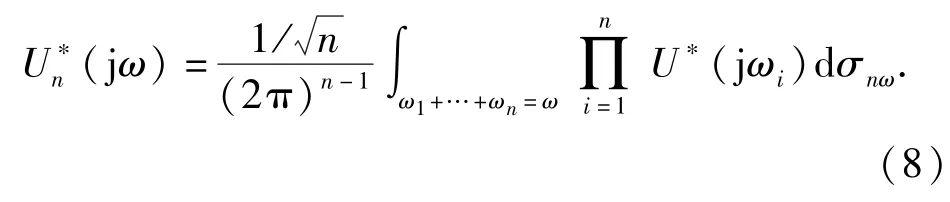
因此,(7)式還可進(jìn)一步改寫為
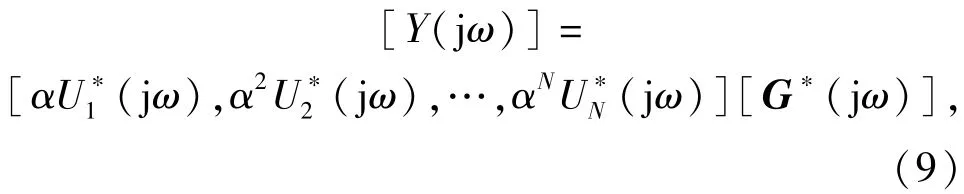
在轉(zhuǎn)子動(dòng)力學(xué)測(cè)試中,一般采用諧波輸入。所謂諧波輸入是指輸入信號(hào)為正余弦輸入信號(hào)。當(dāng)系統(tǒng)在受到諧波信號(hào)輸入時(shí),即
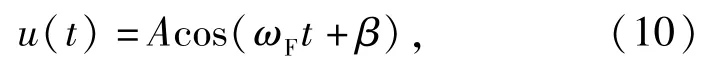
式中:ωF為諧波輸入信號(hào)頻率。根據(jù)文獻(xiàn)[18],(2)式還可以改寫為
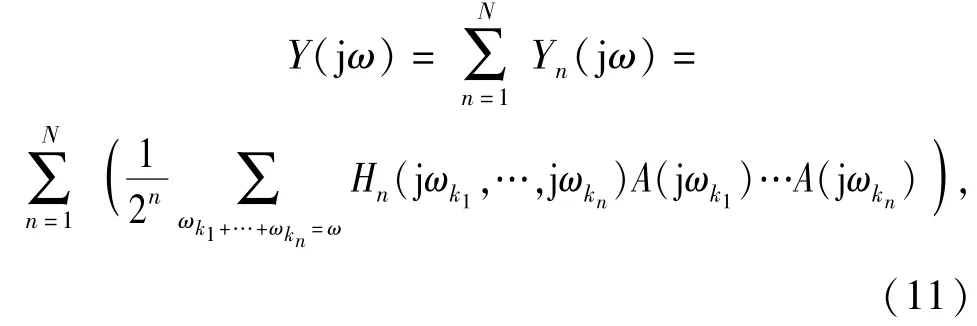
式中:

為了方便起見,定義系統(tǒng)的n階輸出頻率分量為Ωn,則根據(jù)(11)式系統(tǒng)的輸出頻率分量可以表示為

式中:Ωn由頻率集合{ω}確定,即
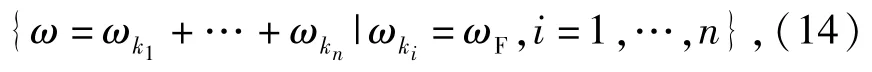
式中:當(dāng)所有的ωk1,…,ωkn均為-ωF時(shí),則ω= -nωF;當(dāng)其中有k個(gè)為ωF時(shí),ω=(-n+2k)ωF.因此輸出Yn(jω)的頻率成分為
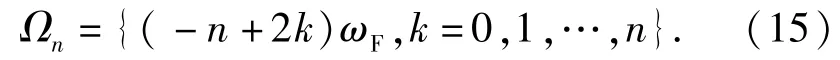
則(13)式進(jìn)一步改寫為
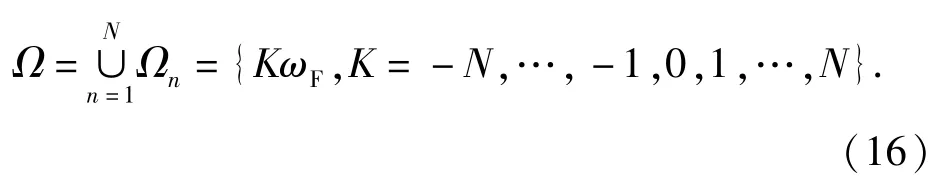
(16)式很好地解釋了非線性系統(tǒng)僅有諧波激勵(lì)時(shí)可以激發(fā)出多次諧波的原因。
因此,非線性系統(tǒng)的輸出頻譜Y(jω)為
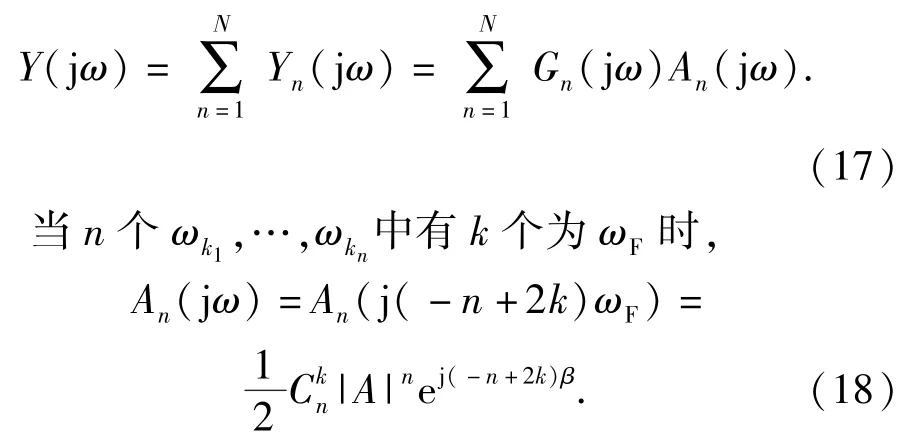
在采用NOFRF分析轉(zhuǎn)子系統(tǒng)的故障特性時(shí),由于4倍頻以上的頻率成分幅值很小,可以忽略不計(jì),而且階數(shù)越高,系統(tǒng)辨識(shí)的計(jì)算量也越大。通常只考慮到前4階頻率輸出即可。因此,由(17)式,并考慮(18)式,可以得到如下4個(gè)式子:
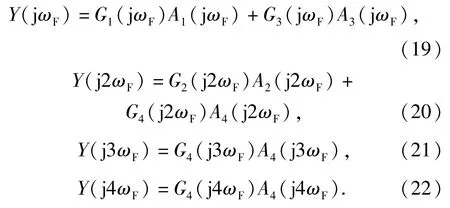
分析(19)式~(22)式可以發(fā)現(xiàn),采用兩個(gè)頻率相同但幅值不同的諧波激勵(lì)信號(hào)去激勵(lì)系統(tǒng),便可以求出系統(tǒng)各階NOFRF值。例如,采用兩個(gè)幅值分別為U(1)、U(2)的正弦波信號(hào)激勵(lì)系統(tǒng),對(duì)應(yīng)系統(tǒng)的輸入頻譜為A(1)q(jωF)、A(2)q(jωF),q=1,2,3,4.相應(yīng)的輸出頻譜為Y(1)(jωF)和Y(2)(jωF).根據(jù)(19)式得
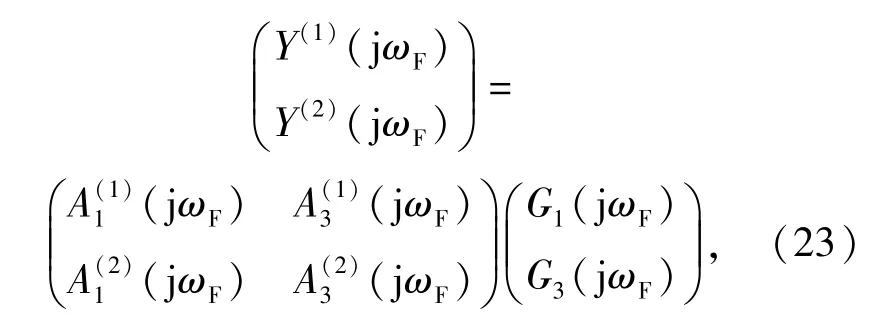
即
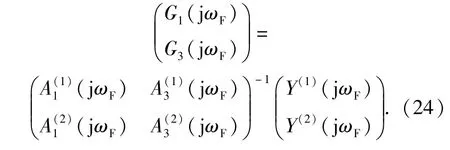
同理,轉(zhuǎn)子系統(tǒng)其他各階NOFRF值均可通過(guò)(19)式~(22)式的變換求得。
2 實(shí)驗(yàn)研究
圖3所示為轉(zhuǎn)子實(shí)驗(yàn)臺(tái)示意圖,轉(zhuǎn)子上兩裂紋分別為橫向裂紋且緊鄰中間轉(zhuǎn)盤左右兩側(cè),通過(guò)安裝在支承座上的電渦流傳感器采集裂紋轉(zhuǎn)子的振動(dòng)位移信號(hào)。取10根相同屬性的轉(zhuǎn)軸用于實(shí)驗(yàn)研究,其中1根轉(zhuǎn)軸不作處理用于比較,另外9根轉(zhuǎn)軸采用線切割技術(shù)加工得到不同的裂紋軸。根據(jù)加工裂紋的深度把這些裂紋軸分成3組。第1組兩裂紋相對(duì)深度比均為a/R=0.2,兩條橫向裂紋在其轉(zhuǎn)軸左端面上投影的裂紋夾角γ分別為0°、45°、90°.第2組左側(cè)裂紋相對(duì)深度比為a1/R=1.0,右側(cè)裂紋相對(duì)深度比為a2/R=0.2,投影面上的裂紋夾角γ分別為0°、45°、90°.第3組裂紋相對(duì)深度比均為a/R=1.0,裂紋夾角γ分別為0°、45°、90°.所有裂紋軸都具有相同的幾何尺寸和材料屬性,即裂紋軸的長(zhǎng)度L=260 mm,裂紋軸直徑為d=9.5 mm,彈性模量E=210 GPa,泊松比ν=0.3,阻尼系數(shù)c= 41.65 kg/s,轉(zhuǎn)盤尺寸φ76 mm×25 mm,轉(zhuǎn)盤質(zhì)量m=0.595 kg,轉(zhuǎn)盤的不平衡偏心距e=0.16 mm,無(wú)裂紋時(shí)轉(zhuǎn)子系統(tǒng)橫向振動(dòng)固有頻率為98.8 Hz.由于轉(zhuǎn)子上裂紋的存在,其固有頻率會(huì)發(fā)生變化,但變化相對(duì)較小,且裂紋轉(zhuǎn)子在1/2固有頻率處的振動(dòng)特性比較明顯,所以在實(shí)驗(yàn)研究中設(shè)定裂紋轉(zhuǎn)子轉(zhuǎn)速n=3 000 r/min.對(duì)該非線性轉(zhuǎn)子系統(tǒng)橫向方向上的輸入輸出進(jìn)行同步采樣,采樣時(shí)每周采樣64個(gè)點(diǎn),采樣8個(gè)周期。
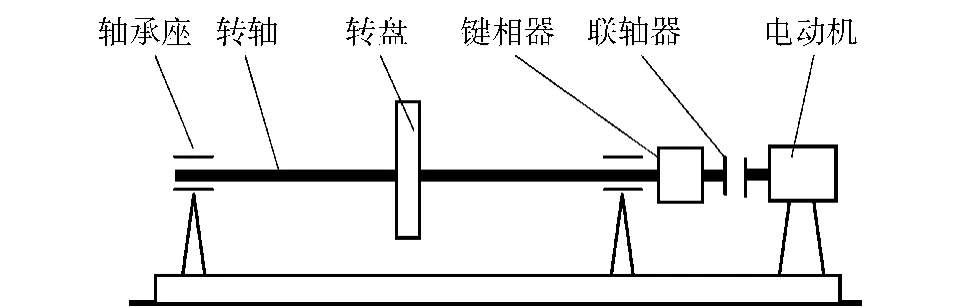
圖3 轉(zhuǎn)子實(shí)驗(yàn)臺(tái)示意Fig.3 Schematic diagram of rotor test bench
首先,從轉(zhuǎn)子系統(tǒng)輸出頻譜上對(duì)該非線性系統(tǒng)進(jìn)行分析。圖4所示為該實(shí)驗(yàn)臺(tái)采集得到的無(wú)裂紋轉(zhuǎn)子系統(tǒng)輸出頻譜圖。從圖中可知,無(wú)裂紋轉(zhuǎn)子正常工作下的輸出頻譜是典型的基頻振動(dòng),其他頻率成分非常微弱,可以忽略不計(jì)。
圖5所示為當(dāng)兩條裂紋均為淺裂紋,即兩裂紋相對(duì)深度比a1/R=a2/R=0.2時(shí),裂紋轉(zhuǎn)子系統(tǒng)輸出頻譜圖。從圖中可以清晰地發(fā)現(xiàn),兩條裂紋在不同裂紋夾角下系統(tǒng)的輸出頻譜會(huì)呈現(xiàn)有規(guī)律的變化,即隨著兩條裂紋夾角逐漸增大,1倍頻幅值無(wú)明顯變化,2倍頻變化明顯且其幅值隨著裂紋夾角的增加而減小;當(dāng)兩條裂紋夾角γ為0°和45°時(shí),會(huì)有微弱的3倍頻出現(xiàn),當(dāng)兩條裂紋夾角γ=90°時(shí),反復(fù)實(shí)驗(yàn)均可發(fā)現(xiàn)此時(shí)系統(tǒng)輸出頻譜中2倍頻、3倍頻分量幅值不再突出,單獨(dú)就該裂紋夾角下的頻譜圖而言,得到的輸出頻譜特性和無(wú)裂紋軸的輸出頻譜特性非常類似,這時(shí),僅從頻譜圖中無(wú)法準(zhǔn)確地推斷轉(zhuǎn)子系統(tǒng)上是否有裂紋存在。
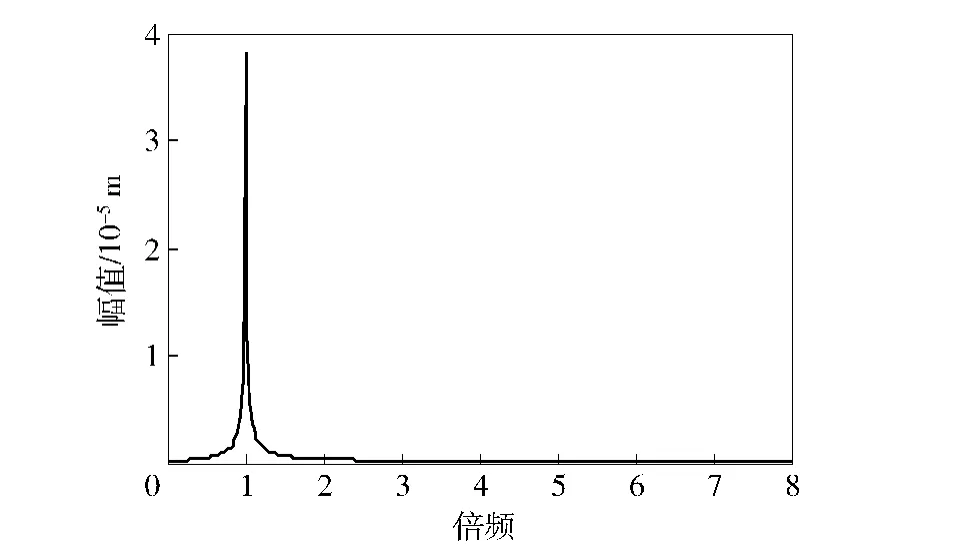
圖4 無(wú)裂紋軸系統(tǒng)輸出頻譜Fig.4 The output spectrum(normal rotor)
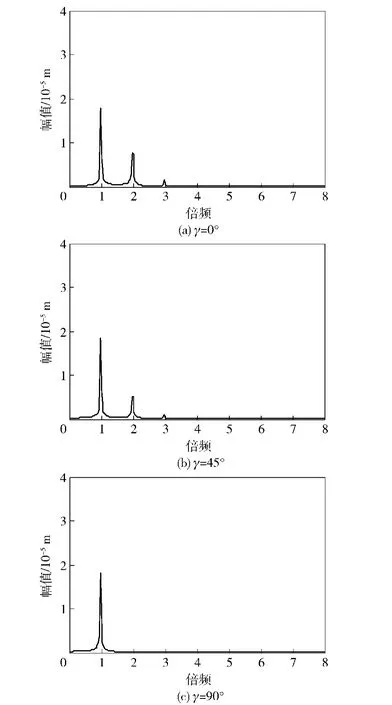
圖5 a1/R=a2/R=0.2時(shí)系統(tǒng)輸出頻譜Fig.5 The output spectrum for a1/R=a2/R=0.2
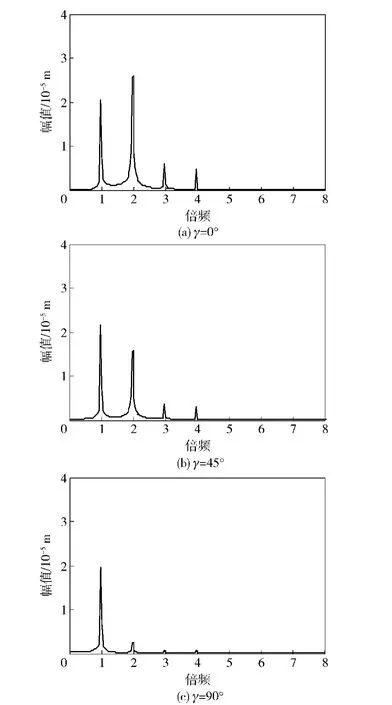
圖6 a1/R=1.0和a2/R=0.2時(shí)系統(tǒng)輸出頻譜Fig.6 The output spectrum for a1/R=1.0 and a2/R=0.2
圖6所示為左側(cè)裂紋相對(duì)深度比a1/R=1.0,右側(cè)裂紋相對(duì)深度比a2/R=0.2下,具有兩條裂紋的轉(zhuǎn)子系統(tǒng)輸出頻譜圖。比較圖5和圖6可以發(fā)現(xiàn),增加左側(cè)裂紋深度使其由淺裂紋變?yōu)樯盍鸭y后,系統(tǒng)輸出頻譜中1倍頻、2倍頻仍舊明顯,同時(shí)伴有3倍頻,4倍頻等多倍頻分量的出現(xiàn),且當(dāng)兩裂紋夾角較小時(shí)多倍頻分量非常明顯。因此,增加轉(zhuǎn)子系統(tǒng)上裂紋深度,系統(tǒng)輸出頻譜中各倍頻分量幅值增加并伴有更多倍頻成分出現(xiàn),系統(tǒng)表現(xiàn)出更強(qiáng)的非線性特性。觀察圖6中不同裂紋夾角下系統(tǒng)輸出頻譜圖,可以發(fā)現(xiàn)與圖5具有相似的變化規(guī)律,即隨著兩條裂紋夾角逐漸增大,基頻幅值變化微弱,2倍頻、3倍頻、4倍頻等多倍頻分量幅值會(huì)隨著兩裂紋夾角的增大而不斷減小,且2倍頻分量幅值變化最為顯著。當(dāng)γ=90°時(shí),多倍頻分量雖然存在但并不明顯。
圖7所示為兩裂紋相對(duì)深度比都為1.0,即a1/R=a2/R=1.0下,具有兩條裂紋的轉(zhuǎn)子系統(tǒng)的輸出頻譜圖。該圖再次驗(yàn)證了圖6得到的結(jié)論,即當(dāng)兩裂紋較深時(shí),系統(tǒng)輸出頻譜中1倍頻、2倍頻仍舊明顯,同時(shí)會(huì)伴有3倍頻、4倍頻等多倍頻的出現(xiàn),系統(tǒng)輸出頻譜中各倍頻分量幅值也會(huì)增加,系統(tǒng)表現(xiàn)出更強(qiáng)的非線性特性。不同的是,當(dāng)兩裂紋深度均較深時(shí),輸出頻譜中3倍頻非常明顯且其幅值遠(yuǎn)大于較為明顯的4倍頻分量幅值。同時(shí),隨著兩條裂紋夾角逐漸增大,2倍頻、3倍頻、4倍頻等多倍頻分量幅值仍舊隨著兩裂紋夾角的增大而不斷減小,在該變化過(guò)程中,2倍頻分量幅值變化最為顯著。
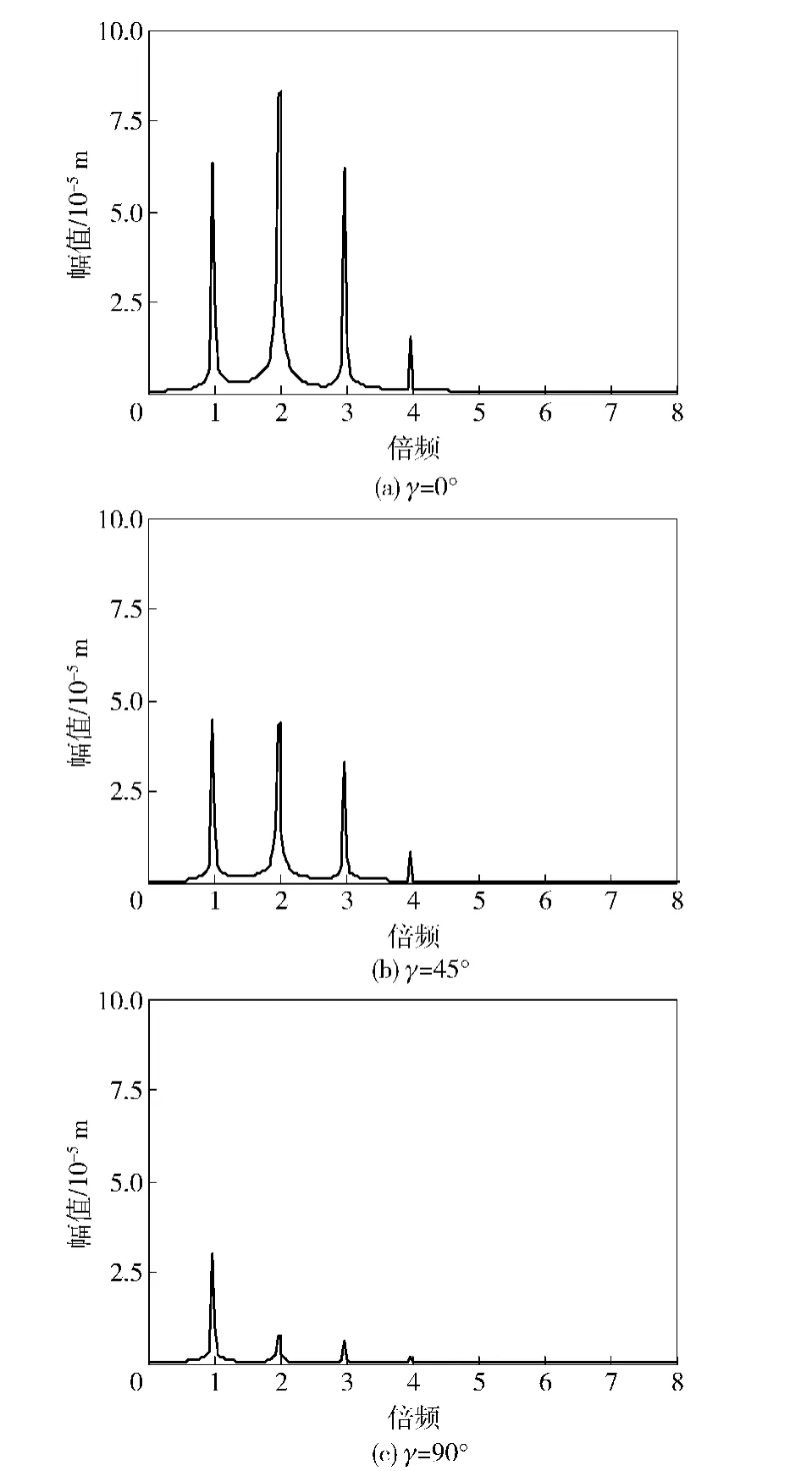
圖7 a1/R=a2/R=1.0時(shí)系統(tǒng)輸出頻Fig.7 The output spectrum for a1/R=a2/R=1.0
整體來(lái)看,該轉(zhuǎn)子系統(tǒng)輸出頻譜中2倍頻、3倍頻、4倍頻等多倍頻分量幅值的變化可有效反應(yīng)轉(zhuǎn)子系統(tǒng)上兩裂紋夾角的變化情況,且2倍頻分量幅值的變化最為顯著。同時(shí),隨著裂紋深度的增加,系統(tǒng)輸出頻譜圖上會(huì)有更多的倍頻分量出現(xiàn)且較為明顯,系統(tǒng)表現(xiàn)出更強(qiáng)的非線性特性。
然后,再?gòu)母麟A非線性輸出頻率響應(yīng)函數(shù)特性上對(duì)該非線性系統(tǒng)進(jìn)行分析,利用(19)式~(22)式得到的不同裂紋深度、不同裂紋夾角的裂紋軸的各階NOFRF值如表1~表3所示,表中所有的數(shù)據(jù)都進(jìn)行了處理,即用得到的各階NOFRF值均除以G1(jωF)得到不大于1的數(shù)。對(duì)于無(wú)裂紋轉(zhuǎn)軸,經(jīng)過(guò)理論推導(dǎo),其應(yīng)該只有G1(jωF)值不為0,其他各階NOFRF值均為0.而通過(guò)該方法的辨識(shí),得到的輸出頻率響應(yīng)函數(shù)中其他各階NOFRF值結(jié)果并不為0,這主要是由隨機(jī)信號(hào)的干擾和計(jì)算誤差所致。然而,與相比較,其他各階NOFRF值都非常小,幾乎可以忽略不計(jì)。因此,對(duì)于無(wú)裂紋轉(zhuǎn)軸,值可以完全反映了系統(tǒng)的本質(zhì)傳遞特性。

表1 a/R=0.2時(shí)不同裂紋夾角下辨識(shí)系統(tǒng)的NOFRF值Tab.1 NOFRF values(a/R=0.2)

表2 a1/R=1.0和a2/R=0.2時(shí)不同裂紋夾角下辨識(shí)系統(tǒng)的NOFRF值Tab.2 NOFRF values(a1/R=1.0,a2/R=0.2)

表3 a/R=1.0時(shí)不同裂紋夾角下辨識(shí)系統(tǒng)的NOFRF值Tab.3 NOFRF values(a/R=1.0)
對(duì)于表1中,當(dāng)兩裂紋均為淺裂紋,裂紋夾角γ=90°時(shí),與無(wú)裂紋軸相比較,除以外的其他NOFRF值均遠(yuǎn)大于無(wú)裂紋軸的NOFRF值,這些NOFRF值的大小反映了監(jiān)測(cè)系統(tǒng)的非線性特性,而在轉(zhuǎn)子上存在淺裂紋時(shí)的頻譜圖中是反映不出來(lái)的,顯示了該方法的獨(dú)特優(yōu)勢(shì)。因此,該方法有效地解決了當(dāng)轉(zhuǎn)子上存在淺裂紋時(shí),采用研究該系統(tǒng)輸出頻譜特性的方法對(duì)裂紋夾角γ=90°時(shí)的裂紋故障無(wú)法檢測(cè)的問題。
3 結(jié)論
相對(duì)單條轉(zhuǎn)子裂紋的故障診斷,多條裂紋的故障診斷更復(fù)雜,也更困難。基于NOFRF的獨(dú)特特性,即該理論不僅能清晰準(zhǔn)確地反映出系統(tǒng)輸出頻譜與非線性參數(shù)之間的關(guān)系,而且各階次的函數(shù)都是一維的。基于此,本文將非線性輸出頻率響應(yīng)函數(shù)理論引入到具有兩條裂紋的轉(zhuǎn)子系統(tǒng)的故障診斷中,利用該方法對(duì)比分析了兩條裂紋不同夾角、不同的裂紋深度下的各階NOFRF值的變化,并得到了一些非常有價(jià)值的結(jié)論,具有重要的理論價(jià)值和工程應(yīng)用價(jià)值。
1)當(dāng)轉(zhuǎn)子系統(tǒng)上有淺裂紋存在時(shí),若采用傳統(tǒng)的頻譜圖分析方法對(duì)轉(zhuǎn)子裂紋故障的存在無(wú)法辨識(shí)時(shí),可以利用NOFRF對(duì)裂紋故障的敏感性有效地克服其不足,實(shí)現(xiàn)轉(zhuǎn)子裂紋故障的有效檢測(cè)。2)在無(wú)裂紋的轉(zhuǎn)子系統(tǒng)正常運(yùn)行狀態(tài)下,值可以完全反映系統(tǒng)的本質(zhì)傳遞特性,其他各階核值與G1(jωF)相比較,幾乎可以忽略不計(jì),一旦裂紋出現(xiàn),各階NOFRF值急劇增大。3)NOFRF值不僅能反映轉(zhuǎn)子系統(tǒng)裂紋的存在,而且能反映兩條裂紋之間的夾角、裂紋深度的變化情況。NOFRF值中的變化情況對(duì)兩條裂紋的夾角非常敏感,尤其G2(j2ωF)隨著兩裂紋夾角的增大而大幅減小;NOFRF值中的變化情況可用于判定裂紋轉(zhuǎn)子系統(tǒng)中兩條裂紋深度的變化情況,即隨著裂紋深度的增加,逐漸變大。
(
)
[1]Armor A F.On-line monitoring of turbine-generator shaft cracking,83-JPGC-Pwr-7[R].US:ASME,1983.
[2]向家偉,陳雪峰,何正嘉,等.基于小波有限元和遺傳優(yōu)化算法的轉(zhuǎn)軸裂紋診斷[J].機(jī)械強(qiáng)度,2008,30(5):702-706. XIANG Jia-wei,CHEN Xue-feng,HE Zheng-jia,et al.Crack diagnosis for the shaft based on wavelet finite element method and genetic algorithm[J].Journal of Mechanical Strength,2008,30(5):702-706.(in Chinese)
[3]Yu Z G,Chu F L.Identification of crack in functionally graded material beams using the p-version of finite element method[J]. Journal of Sound and Vibration,2009,325(1/2):69-84.
[4]謝平,杜義浩.基于信息熵的裂紋轉(zhuǎn)子動(dòng)力特征分析與診斷方法[J].機(jī)械工程學(xué)報(bào),2009,45(1):195-199. XIE Ping,DU Yi-hao.Crack rotor dynamic feature analysis and diagnosis method based on information entropy[J].Journal of Mechanical Engineering,2009,45(1):195-199.(in Chinese)
[5]陳雪峰,向家偉,董洪波,等.基于區(qū)間B樣條小波有限元的轉(zhuǎn)子裂紋定量識(shí)別[J].機(jī)械工程學(xué)報(bào),2007,43(3):123-127. CHEN Xue-feng,XIANG Jia-wei,DONG Hong-bo.et al.Quanti-tative identification of rotor cracks based on finite element of B-spline wavelet on the interval[J].Journal of Mechanical Engineering,2007,43(3):123-127.(in Chinese)
[6]Li X J,Wang K,Jiang L P,et al.The application of a signal in early cracked rotor fault diagnosis with pwvd and svm[J].Journal of Software,2011,6(10):1969-1976.
[7]Darpe A K,Gupta K,Chawla A.Dynamics o f a twocrack rotor[J]. Journal of Sound and Vibration,2003,259(3):649-675.
[8]于濤,孫偉,韓清凱.雙裂紋轉(zhuǎn)子系統(tǒng)非線性動(dòng)力學(xué)特性研究[J].振動(dòng)與沖擊,2013,32(19):144-152. YU Tao,SUN Wei,HAN Qing-kai.Nonlinear dynamic behavior of a dual-crack rotor system[J].Journal of Sound and Vibration,2013,32(19):144-152.(in Chinese)
[9]溫詩(shī)鑄,郭丹.具有兩條裂紋的轉(zhuǎn)子系統(tǒng)的振動(dòng)研究[J].機(jī)械強(qiáng)度,2005,27(2):135-139. WEN Shi-zhu,GUO Dan.Vibration analysis of a rotor with two cracks[J].Journal of Mechanical Strength,2005,27(2):135-139.(in Chinese)
[10]Chasalevris A C.Identification of multiple cracks in beams under bending[J].Mechanical System and Signal Processing,2006,20(7):1631-1673.
[11]Lang Z Q,Billings S A,Yue R,et al.Output frequency response function of nonlinear volterra systems[J].Automatica,2007,43(5):805-816.
[12]Lang Z Q,Billings S A.Energy transfer properties of nonlinear systems in the frequency domain[J].Journal of Sound and Vibration,2005,78(5),354-362.
[13]Lang Z Q,Peng Z K.A novel approach for nonlinearity detection in vibrating systems[J].Journal of Sound and Vibration,2008,314(3/4/5):603-615.
[14]Lang Z Q,Billings S A,Tomlinson G R,et al.Analytical description of the effects of system nonlinearities on output frequency responses:a case study[J].Journal of Sound and Vibration,2006,295(3/4/5):584-601.
[15]Peng Z K,Lang Z Q.The nonlinear output frequency response functions of one-dimensional chain type structures[J].Journal of Applied Mechanics,2010,77(1):11-27.
[16]Peng Z K,Lang Z Q,Billings S A,et al.Analysis of locally nonlinear MDOF systems using nonlinear output frequency response functions[J].Journal of Vibration and Acoustics,2009,131(5):51-63.
[17]Peng Z K,Lang Z Q,Billings S A,et al.Crack detection using nonlinear output frequency response functions[J].Journal of Sound and Vibration,2007,301(3/4/5):777-788.
[18]Peng Z K,Lang Z Q,Billings S A,etc.Analysis of bilinear oscillators under harmonic loading using nonlinear output frequency response functions[J].International Journal of Mechanical Sciences,2007,49(11):1213-1225.
[19]員險(xiǎn)鋒,李志農(nóng),林言麗,等.基于非線性輸出頻率響應(yīng)函數(shù)的裂紋故障診斷方法研究[J].機(jī)械強(qiáng)度,2013,35(2): 133-137. YUAN Xian-feng,LI Zhi-nong,LIN Yan-li,et al.Rotor crack fault diagnosis method based on nonlinear output frequency response function[J].Journal of Mechanical Strength,2013,35(2):133-137.(in Chinese)
[20]員險(xiǎn)鋒.基于非線性輸出頻率響應(yīng)函數(shù)的轉(zhuǎn)子裂紋故障診斷方法研究[D].鄭州:鄭州大學(xué),2011. YUAN Xian-feng.Crack rotor fault diagnosis method based on nonlinear output frequency response function[D].Zhengzhou: Zhengzhou University,2011.(in Chinese)
Fault Diagnosis Method of Rotor System with Multi-crack Based on Nonlinear Output Frequency Response Function
LI Zhi-nong,DU Yi-guang,XIAO Yao-xian
(School of Aeronautical Manufacturing Engineering,Nanchang Hangkong University,Nanchang 330063,Jiangxi,China)
The fault diagnosis of rotor system with multi-crack is more complex and more difficult than the fault diagnosis of rotor system with single crack.The nonlinear output frequency response function(NOFRF)is introduced to fault diagnosis of rotor system with two cracks,and a fault diagnosis method of rotor system with two cracks based on the NOFRF is proposed.The NOFRF values of two cracks with different crack angles and crack depths are compared.The experimental results show that the NOFRF values are very sensitive to different crack angles and different crack depths,and the existence of rotor crack fault and the variation of crack angle and crack depth can be reflected by the NOFRF values.Therefore,the sensitivity of the NOFRF values to the crack fault can be effectively used for the detection of a rotor system with multi-cracks.
power machinery engineering;nonlinear output frequency response function;cracked rotor;fault diagnosis;crack angle;crack depth
O347.6;TH165.3
A
1000-1093(2015)06-1096-08
10.3969/j.issn.1000-1093.2015.06.019
2014-09-09
國(guó)家自然科學(xué)基金項(xiàng)目(51265039、51075372、50775208)
李志農(nóng)(1966—),男,教授。E-mail:lizhinong@tsinghua.org.cn

