離散數(shù)學實驗平臺構建及實驗方法研究

李華昱+張千

摘 要 離散數(shù)學是計算機專業(yè)一門重要的基礎課，在課堂講授理論知識的同時，它的實驗教學環(huán)節(jié)往往被忽視。本文結合目前離散數(shù)學課堂授課和實驗教學現(xiàn)狀，闡述了實驗教學的重要性，并從實驗教學模式、實驗效果評價、案例教學和實驗內(nèi)容等方面，對提高實驗教學效果的方法進行了分析與研究，并給出了具體的實現(xiàn)方案。

關鍵詞 離散數(shù)學 實驗教學 案例教學 實驗內(nèi)容

中圖分類號：G642.3 文獻標識碼：A DOI：10.16400/j.cnki.kjdkx.2015.10.025

Experimentation Platform Construction and Method

Research of Discrete Mathematics

LI Huayu， ZHANG Qian

（College of Computer and Communication Engineering， China University of Petroleum， Qingdao， Shandong 266580）

Abstract Discrete mathematics is an important foundation course in computer science. In the course of teaching theoretical knowledge， experimental teaching is often ignored.Compared with present situation of classroom instruction and experimental teaching， this paper described the importance of experimental teaching， and from teaching mode， effect evaluation and case teaching aspects， methods of improving experimental teaching effect are analyzed and researched. Moreover，implementation scheme is also given in this paper.

Key words discrete mathematics; experimental teaching; case teaching; experimental contents

0 引言

離散數(shù)學是現(xiàn)代數(shù)學的一個重要分支，在計算機科學中有著極其廣泛的應用，已經(jīng)成為計算機科學與技術專業(yè)重要的專業(yè)基礎課程。通過離散數(shù)學的學習，能夠幫助學生掌握處理離散結構的描述工具和方法，為后續(xù)的“數(shù)據(jù)結構”、“數(shù)據(jù)庫原理”、“操作系統(tǒng)”和“編譯原理”等專業(yè)課程的學習創(chuàng)造條件，還可提高學生抽象思維和邏輯推理能力，為將來參與創(chuàng)新性的研究和開發(fā)工作打下堅實的基礎。①

離散數(shù)學是建立在大量定義之上的邏輯推理學科，對概念、定義的理解是學習這門課程的核心。離散數(shù)學的教學內(nèi)容分為數(shù)理邏輯、集合與關系、代數(shù)系統(tǒng)和圖論四部分，涵蓋了計算機科學與工程實踐所需要的數(shù)學理論和方法。每一部分概念、定理繁多，都具有一定的理論抽象性，各部分之間具有一定的關聯(lián)關系，既涉及具體內(nèi)容，又包含思維方法。目前，由于課時限制，教師在教學過程中只重視理論教學，忽視了實驗教學環(huán)節(jié)，絕大部分課時用于課堂教學，講授抽象的定義描述和定理證明，不注意整理分散的知識點，導致部分學生認為離散數(shù)學是枯燥、如同散沙一般的課程。同時，針對離散數(shù)學的教學研究，也只側重于教學內(nèi)容探討和理論教學方法的改進，對實踐教學討論不多。這種教學模式極大地降低了學生學習的積極性，削弱了離散數(shù)學作為計算機學科基礎理論課的地位，對培養(yǎng)學生解決實際問題能力也起不到應有的作用。

因此，為了更好地提高離散數(shù)學教學質量，增強學生學習效果，一方面需要精選教學內(nèi)容、改進教學方法;另一方面需要加強實驗教學環(huán)節(jié)，通過合理的實驗課時安排、上機操作和實驗案例，將課堂講授的定義、定理、性質和各個上機實驗結果聯(lián)系起來，使學生對抽象的理論知識有一個感性和直觀的理解。

1 改進實驗教學方法

1.1 構建基于網(wǎng)絡的實驗教學平臺

傳統(tǒng)的實驗教學主要采用基于單機的應用模式。授課教師通過單機版實驗程序進行課堂演示，或者由學生自行下載并安裝實驗程序，完成實驗教學。在目前離散數(shù)學實驗課時緊張的情況下，這種單機版應用模式使得學生只能夠在有限的實驗授課時才可以進行上機操作，限制了與授課教師進行交流的有效時間;此外，單純的實驗室上機環(huán)境也制約了學生學習的積極性。

隨著高校實驗設備、硬件設施和網(wǎng)絡環(huán)境的不斷提高與改進，為構建基于校園局域網(wǎng)的離散數(shù)學網(wǎng)絡實驗教學平臺提供了有利條件。為此，可以將實驗教學擴展為基于網(wǎng)絡的B/S（Browser/Server）的網(wǎng)絡實驗模式。該模式打破了以往授課的時間和地域限制，學生既可在實驗室進行上機操作，也可借助網(wǎng)絡，針對特定的實驗案例與教師進行在線或者離線交談，屏蔽了教師和學生之間的地點和時間差異，使教師可以隨時對學生進行在線輔導，為提高課堂教學效果提供了有效的輔助作用。

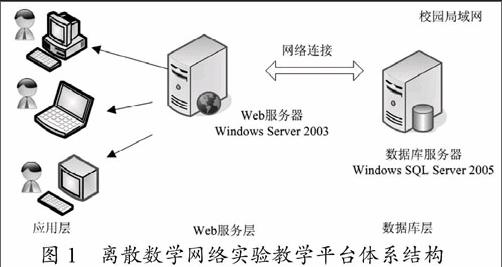
離散數(shù)學網(wǎng)絡實驗教學平臺采用3層架構進行構建，如圖1所示：（1）數(shù)據(jù)庫服務器層：主要存儲和管理實驗案例的基礎數(shù)據(jù)、計算分析數(shù)據(jù)和用戶信息，并為其它兩層提供有效的數(shù)據(jù)服務;（2）Web服務層：該層存放實驗教學平臺所有的實驗案例程序、Web頁面文件和系統(tǒng)配置文件，該層通過校園局域網(wǎng)絡進行服務發(fā)布，能夠及時響應并處理用戶提交的實驗操作請求;（3）應用層：通過分配的賬號信息，學生登錄網(wǎng)絡教學平臺并進入主界面;然后，根據(jù)教師布置的實驗案例任務選擇相關的子頁面;最后，進行案例選擇、模擬演示、編制程序和提交作業(yè)等操作。endprint

圖1 離散數(shù)學網(wǎng)絡實驗教學平臺體系結構

1.2 實驗教學效果實時評價與反饋

目前，離散數(shù)學通常采用“布置任務—演示講解—輔導”的實驗教學模式，即教師首先根據(jù)課堂教學進度布置實驗任務，然后對實驗涉及的關鍵內(nèi)容、操作步驟和程序設計思想進行演示和講解，最后，安排學生上機練習，并針對若干問題對學生進行輔導。然而，教師布置任務和演示講解會占用一定的時間，當班級學生人數(shù)較多時，沒有時間和精力對每個學生進行細致的輔導，而且學生對知識的理解和接受能力往往不同，單純通過教師的演示講解，無法在有限的實驗課時內(nèi)達到較好的效果。

為此，在當前實驗教學模式基礎之上，需要提供有效的教學效果評價和反饋渠道，②使學生能夠實時對教學效果進行實名或者匿名評價，授課教師通過對提交的評價信息進行整理與分析，發(fā)現(xiàn)與了解代表性和針對性強的問題，并及時將解決方法反饋給學生。這種實時評價方式可以借助網(wǎng)絡實驗教學平臺進行實現(xiàn)，學生通過提供的效果評價功能在線提交效果評價數(shù)據(jù)，并可以及時查詢教師的反饋信息，使學生能夠在上課之余得到有效的輔導。

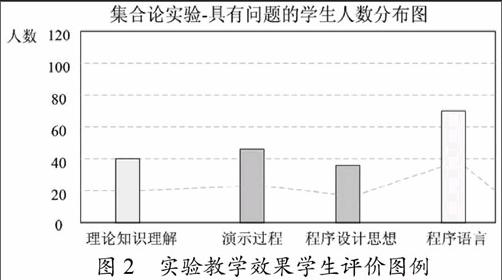
例如，針對集合論中的實驗，學生可以按照自己的理解程度，從“理論知識理解”、“演示過程”、“程序設計思想”和“程序語言”四個方面選擇理解困難的項目，并連同具體的問題提交到評價系統(tǒng)數(shù)據(jù)庫中，評價結果經(jīng)過匯總后，按照圖2所示的方式顯示提交學生的人數(shù)分布情況。借助該評價圖例，教師可以直觀、形象地獲取量化信息，并且能夠針對選定的評價項目，進一步查看具體的評價數(shù)據(jù)。

1.3 注重案例教學法

案例教學是通過具有一定典型意義的事情發(fā)生、發(fā)展的過程，使學生深刻理解理論知識的教學方法。案例教學改變以往以教師為主的課堂教學模式，更加注重學生的過程參與。通過在實踐教學中引入案例教學法，引導學生運用所學定義和定理對案例進行分析討論，不但能夠開拓知識，又能活躍課堂氣氛，激發(fā)學生的學習熱情。

在選擇實驗案例時，應該注重離散數(shù)學與其它專業(yè)課程的相關性。例如：集合論中的序偶和笛卡爾積兩個概念分別在《數(shù)據(jù)結構》和《數(shù)據(jù)庫原理》中有所涉及，在設計該部分的實驗案例時，不僅需要結合定義和定理，而且還應該讓學生了解兩個概念在以上課程中的應用，提高學習的針對性和目的性。為此，結合“斗獸棋”游戲進行案例設計：③“斗獸棋”共有16 顆棋子，可以看成是由A={紅，藍}、B={象，獅，虎，豹，狼，狗，貓，鼠}兩個集合的笛卡爾積AB的一個子集C構成，C={<紅，象>，<紅，獅>，<紅，虎>，<紅，豹>，<紅，狼>，<紅，狗>，<紅，貓>，<紅，鼠>， <藍，象>，<藍，獅>，<藍，虎>，<藍，豹>，<藍，狼>，<藍，狗>，<藍，貓>，<藍，鼠> }，每個棋子是C中的一個序偶元素，該案例能夠使學生借助演示程序對序偶和笛卡爾積有具體形象的理解。關系數(shù)據(jù)模型中表結構、關系操作的查詢與連接都涉及到笛卡兒積的理論，為此，還可以從數(shù)據(jù)庫中的關系數(shù)據(jù)模型角度設計“笛卡兒積”的相關案例。

在設計實驗案例時，不需要詳細、深入地進行算法分析和代碼描述，而是應該結合理論知識，側重講解其應用背景，使學生深刻離散數(shù)學課程的實用價值，激發(fā)自主學習的積極性。

2 實驗內(nèi)容設計

離散數(shù)學的實驗教學內(nèi)容應該依托于課堂授課內(nèi)容，但不能簡單地成為理論知識的教學實踐。實驗教學必須拓展理論教學，作為理論課的補充和加強。在設計離散數(shù)學四部分的實驗教學內(nèi)容時，應該從提高計算機專業(yè)學生的數(shù)學素質和程序設計能力方面出發(fā)，結合各分支的最新研究成果，以培養(yǎng)學生運用離散數(shù)學知識進行數(shù)學建模和解決工程應用問題的能力為目標。

針對不同的教學內(nèi)容，需要設計不同類型的實驗，在具體實驗教學中，需要根據(jù)實驗學時安排，進行選做或全做。

2.1 數(shù)理邏輯實驗設計

可以從課堂授課的理論知識和實際應用領域兩方面進行設計。針對計算機專業(yè)特點，安排VB或者C編程求解命題公式的真值與范式、公式等價證明和命題演算等實驗，讓學生進一步熟練各個聯(lián)結詞和等價公式的求解方法。針對數(shù)理邏輯的實際應用，可以通過高低電平表示的信號運算與二進制運算之間的聯(lián)系，利用數(shù)字邏輯電路理論來設計數(shù)理邏輯方面的實驗，如表決器、搶答器等電路實驗。④

2.2 集合論實驗設計

二元關系是集合論的主要內(nèi)容，可以要求學生利用數(shù)組、向量等數(shù)據(jù)結構，采用C++、Java等編程語言實現(xiàn)集合的并、交、補、差等運算。此外，針對關系的自反、反自反、對稱、反對稱和傳遞五種性質判定等，進行相關的實驗題目設計。⑤對于理論知識扎實和接受能力強的學生，可以進一步安排求解關系閉包和商集的算法實驗。

2.3 代數(shù)結構與代數(shù)系統(tǒng)實驗設計

代數(shù)結構與代數(shù)系統(tǒng)包括半群、群、環(huán)和布爾代數(shù)等概念，在密碼學、通信系統(tǒng)等領域應用十分廣泛，但具體內(nèi)容非常抽象。因此，在設計實驗時，應該圍繞基本定義和定理，安排一些較簡單的實驗，例如，判斷某個集合關于二元運算是否構成半群、獨異點或群。同時，可以針對代數(shù)結構（下轉第52頁）（上接第50頁）在網(wǎng)絡信息安全中的應用，設計演示為主、練習為輔的實驗，如DSA簽名算法等，使學生對抽象的理論知識有一個直觀的認識。

2.4 圖論實驗設計

圖論涉及歐拉圖、哈密爾頓圖、平面圖和樹等。在設計實驗時，應該結合圖在計算機中的表示和運算規(guī)律，首先設計一些基礎的實驗內(nèi)容，如求鄰接矩陣和可達性矩陣等，并根據(jù)這些矩陣找出強分圖、單側分圖和弱分圖;然后，再針對圖論的實際應用，設計與歐拉圖、哈密爾頓圖和樹有關的編程實驗，如獲取城市之間最短通信路徑的算法，哈夫曼編碼問題等。如果課時允許，還可以設置最優(yōu)二叉樹構造和圖的著色算法實驗。

3 結束語

作為計算機專業(yè)的一門重要課程，離散數(shù)學具有理論性強和內(nèi)容抽象等特性。由于離散數(shù)學課時安排緊張，課堂授課主要圍繞理論知識進行講解，很少介紹其應用背景，難以激發(fā)學生的學習興趣。為此，需要重視實驗教學環(huán)節(jié)，在實驗課時有限的情況下，通過多種實驗教學方法，圍繞授課內(nèi)容和應用領域，建立有效和可行的實驗教學模式和實驗內(nèi)容，培養(yǎng)學生學習該課程的興趣，提高離散數(shù)學教學效果。

注釋

① 譚作文.離散數(shù)學課程中實驗教學探討[J].計算機教育，2010（17）：106-109.

② 姜春茂，黃春梅.“離散數(shù)學”實踐教學研究[J].計算機教育，2008（18）：100.

③ 徐杏芳，夏浩波.案例教學法在《離散數(shù)學》中的應用[J].福建電腦，2007（7）：213.

④ 郭詠梅，張劍妹.離散數(shù)學研究性實驗的探索與實踐[J].現(xiàn)代計算機，2014（24）：31-33.

⑤ 鐘敏，時念云.改革課程實驗，提高離散數(shù)學教學質量[J].計算機教育，2008（18）：29-30.endprint