GPU上高光譜快速ICA降維并行算法*
方民權,周海芳,張衛民,申小龍
(國防科技大學 計算機學院, 湖南 長沙 410073)
GPU上高光譜快速ICA降維并行算法*
方民權,周海芳,張衛民,申小龍
(國防科技大學 計算機學院, 湖南 長沙 410073)
高光譜影像降維快速獨立成分分析過程包含大規模矩陣運算和大量迭代計算。通過分析算法熱點,設計協方差矩陣計算、白化處理、ICA迭代和IC變換等關鍵熱點的圖像處理單元映射方案,提出并實現一種G-FastICA并行算法,并基于GPU架構研究算法優化策略。實驗結果顯示:在處理高光譜影像降維時,CPU/GPU異構系統能獲得比CPU更高效的性能,G-FastICA算法比串行最高可獲得72倍加速比,比16核CPU并行處理快4~6.5倍。
圖像處理單元;高光譜影像降維;快速獨立成分分析;并行算法;性能優化
(CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073,China)
高光譜遙感技術廣泛應用于軍事、農業、環境科學、地質、海洋學等領域,這些領域迫切要求及時處理[1]。但高光譜影像數據有波段多、數據量大、相關性強、冗余多等特點,直接處理將導致維數災難、空空間現象等嚴重的計算問題[2-4]。因此,國內外專家學者處理高光譜影像數據過程常常包括降維步驟。降維通過一定的映射,將高維影像數據轉換成低維影像數據,并保持信息量基本不變。
高光譜影像降維方法可分為線性和非線性兩大類:線性降維有主成分分析(PrincipalComponentAnalysis,PCA)[5]、獨立成分分析(IndependentComponentAnalysis,ICA)[6]等方法;非線性降維包括基于核的方法和基于流行學習的方法,如等距映射法(ISOmetricMAPping,ISOMAP)[7]、局部線性嵌入(LocallyLinearEmbedding,LLE)[8]等。獨立成分分析是應用最廣泛的降維方法之一,其降維過程包含了大規模矩陣計算和大量迭代運算。由于高光譜影像波段多、數據量大等特征,降維處理過程復雜且耗時,傳統的串行降維已無法滿足各行業的需求,因此并行降維的研究已迫在眉睫。
自2007年Nvidia正式推出統一計算設備架構(ComputeUnifiedDeviceArchitecture,CUDA)以來,圖像處理單元在通用計算領域發展迅猛。CPU/GPU的異構系統可編程性好、性價比高、功耗比低,已成為高性能計算領域的黑馬。搭載這種異構系統的天河1A和泰坦分別在2010年和2012年奪得TOP500榜首[9]。CPU/GPU異構系統的快速發展為高光譜影像降維的實時處理提供了可能。
高光譜影像并行處理在傳統并行系統中已有成熟的應用,David等[10]基于異構訊息傳遞接口(MessagePassingInterface,MPI)在網絡集群系統研究了高光譜影像處理的技術;Javier等[11]提出基于神經網絡的高光譜影像并行分類算法。在CPU/GPU異構系統上,Sanchez等[12]對高光譜解混進行了GPU移植;Yang等[13]利用多GPU實現了高光譜影像快速波段選擇;Rui等[14]在GPU上實現FastICA算法,加速55倍;Jacquelyne等[15]用OpenCL在GPU上實現InfomaxICA,最高加速56倍。但這些研究較少涉及基于GPU研究高光譜影像降維。本文研究基于負熵最大的FastICA降維算法[16-17],針對算法熱點設計GPU映射方案,最終提出并實現一種G-FastICA并行算法。
1 FastICA算法與熱點分析
1.1 基于負熵最大的FastICA
FastICA算法有基于負熵最大、基于似然最大、基于峭度3種形式,本文主要研究基于負熵最大的FastICA算法。該算法是盲源降維方法,以負熵最大為搜尋方向,實現獨立源的順序提取,采用定點迭代的優化方法,收斂更加快速、穩健[16-17]。
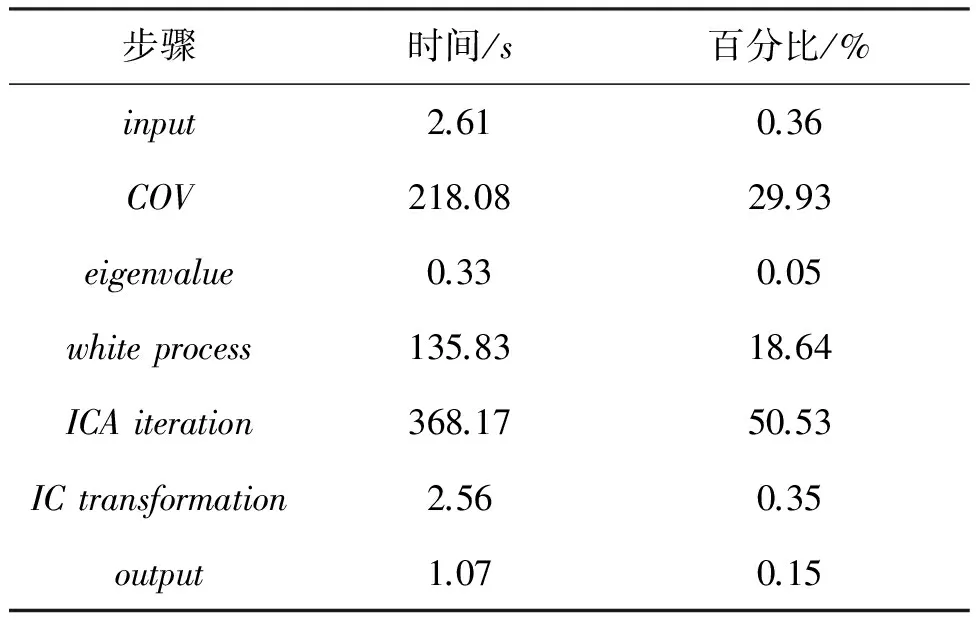
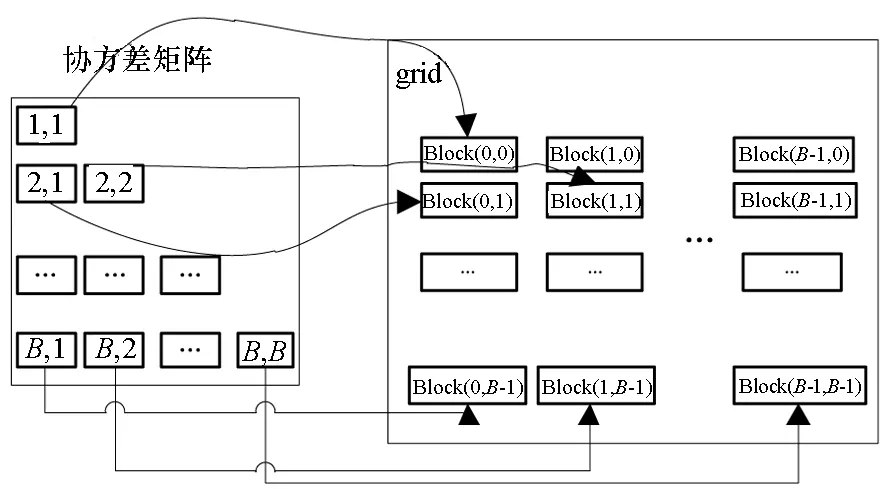
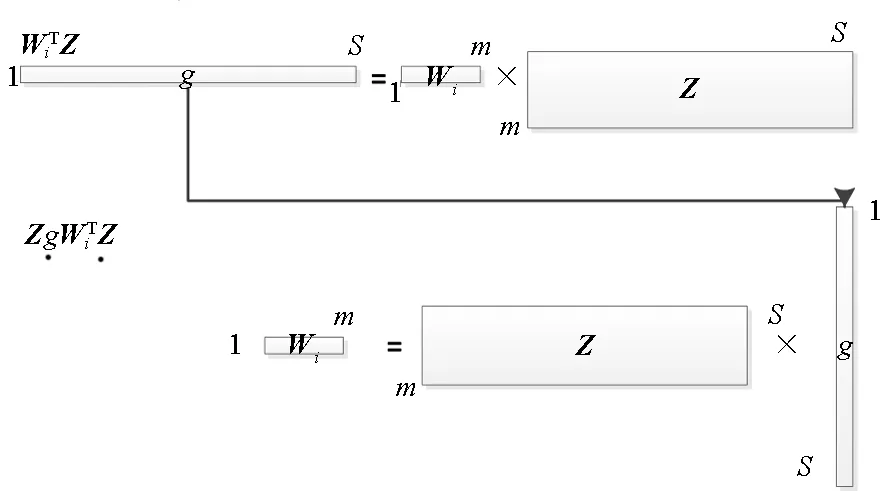
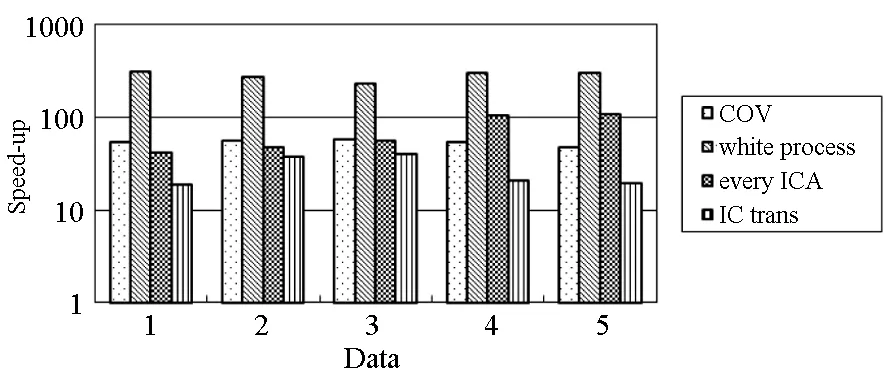
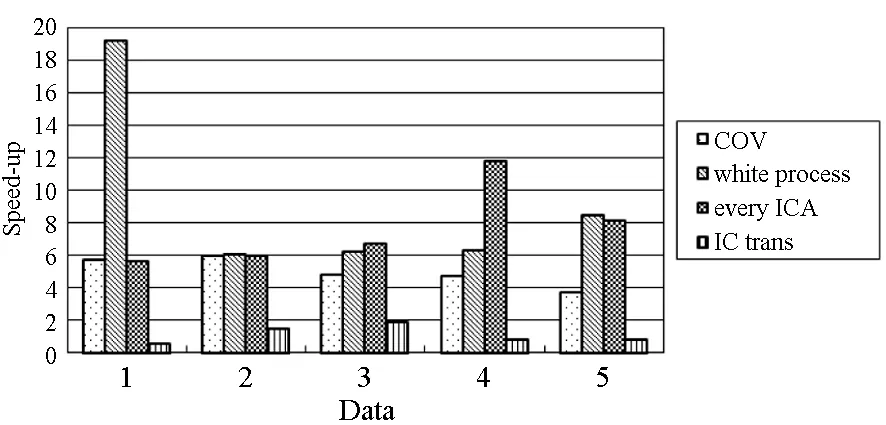
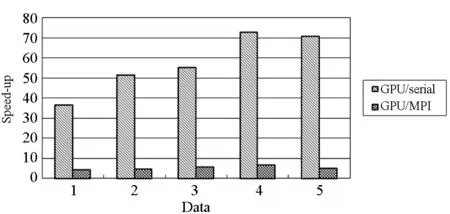
對于高光譜影像數據X(W×H×B,寬W、高H、波段B),X可視為B行S列(S=W×H)的二維矩陣,矩陣的一行表示一個波段的高光譜影像數據。通過獨立成分分析方法降維,可以獲得m個IC圖像,其中m step1.計算X的協方差矩陣; step2.計算協方差矩陣的特征值及特征向量,并根據閾值T選取最終IC圖像數量m; step3.計算白化矩陣M=D-1/2VT,其中D為X的特征值矩陣,V為對應的特征向量矩陣; step4.高光譜影像數據白化處理Z=MX,X要減去均值(即零均值處理),M為白化矩陣,Z為白化處理結果矩陣; step5.迭代開始: ①初始化Wi,Wi為變換矩陣W的一列; 其中g為非線性函數,經測試,取g(y)=y3可更穩定、更快地達到ICA迭代收斂。 ④歸一化Wi=Wi/‖Wi‖; ⑤判斷是否收斂,不收斂則返回到步驟②,若收斂,如果所有的Wi已經計算結束(即i=m),則退出,否則令i=i+1,返回到步驟①計算Wi; step6.計算獨立成分Y=WZ; 1.2 加速熱點分析 實現串行高光譜影像FastICA降維算法,對寬781、高6955、波段數224的高光譜影像降維,測試并統計各步驟占總計算時間的比率(見表1)。表中數據顯示,協方差矩陣計算(COV)、白化處理(whiteprocess)和ICA迭代(ICAiteration)過程比重較大,共占總計算時間的99%,是并行研究的關鍵熱點。此外特征值計算取決于波段數B,本文數據波段數均為224,因此特征值特征向量的計算屬于不變串行分量,無須考慮并行;IC變換(ICtransformation)、數據I/O與高光譜影像數據的寬、高、波段數及其信息特征相關,作為次要熱點考慮其并行化。 表1 FastICA時間分布 2.1 協方差矩陣計算的GPU映射 協方差矩陣是對稱陣,僅需計算其下三角元素,再將值填入對應的上三角陣。針對該過程,設計了一種映射方案:GPU上的每個線程塊完成協方差矩陣中一個協方差的計算任務,如圖1所示。啟動B×(B+1)/2個block,每個block中的thread數量可根據occupancy選取最佳的thread數。其思想是將協方差矩陣中單個協方差的計算任務映射到對應的block中,由一個block完成一個協方差元素的計算。一種實現策略是:每次啟動維度為<< 圖1 協方差矩陣的GPU映射方案Fig.1 GPU mapping scheme of covariance matrix 2.2 設備端并行白化處理 GPU是細粒度并行協處理器,在白化處理中尋找細粒度的并行計算任務,再將這些細粒度計算任務通過kernel函數映射到GPU核上執行,這是設備端并行白化處理的關鍵。 在白化處理(Z=MX)中,M是B×m的矩陣,X的尺寸為S×B,結果矩陣Z大小為S×m。結果矩陣每個元素的計算是獨立的,且計算任務量類似,是長為B的向量內積。高光譜影像的波段數B一般為幾十到上百不等,即向量內積的運算量有限,是細粒度任務,故視結果矩陣的單個元素的計算為單元任務,將其映射到GPU的thread上。整個結果矩陣共有S×m個單元任務,需要S×m個線程參與計算;但高光譜影像的寬W和高H較大(約數百到上千),故S=W×H較大,S×m的數量級更大,超過GPU一次可啟動的最大線程數量,無法直接運算。此時,采用循環計算的方法,即啟動適當數量的block和thread,多次循環完成計算任務。對于線程塊blockIdx中的線程threadIdx,需計算索引為i×(gridDim×blockDim)+blockIdx×blockDim+threadIdx的任務(i為循環變量),直到索引超過S×m。該方案中,gridDim和blockDim不受算法自身約束,可根據occupancy自由設定,以最大化GPU設備占用率,從而獲得最佳性能。 2.3 ICA迭代的GPU移植 ICA迭代過程中,受數據依賴限制,不同迭代無法同時運算,只能在單次迭代中開發并行。分析迭代中各個步驟的計算量,初始化、正交化、歸一化和判斷操作的計算量很小,可不必考慮,主要的計算量集中在步驟②中。分解該步驟,抽象得到圖2所示的ICA迭代宏觀模型。 圖2 ICA迭代關鍵步驟模型Fig.2 Model of key step for ICA iteration 2.4 G-FastICA算法 IC變換與白化處理的運算模型類似,因此將前文設計的白化處理并行策略套用到IC變換中。高光譜影像數據I/O的并行化依賴于并行文件系統或緩存機制,利用多線程技術,每個線程創建獨立的文件指針,通過合理的數據分割,各個線程將指針指向各自的目標位置,再進行輸入輸出操作。 針對單GPU,根據前面提出的協方差矩陣計算、白化處理、ICA迭代、IC變換等熱點的GPU映射并行方案,用其替代串行算法的對應步驟,可實現CPU與GPU協同計算高光譜影像FastICA降維過程,稱之為G-FastICA算法。 基于GPU的計算通信重疊優化:協方差矩陣計算,存在著計算通信重疊的可能性。由圖1可知,第i行計算使用高光譜影像數據前i個波段的數據。傳輸完第1個波段數據后,協方差矩陣第1行計算和第2波段數據傳輸可同時進行,此時計算與通信能夠重疊。采用多流的方法實現GPU計算與CPU/GPU通信的并發執行。得益于計算通信重疊,幾乎能掩蓋全部高光譜影像數據傳輸時間。 GPU存儲優化:GPU提供了層次分明的存儲單元系統,按離核距離由近及遠分別是寄存器、共享存儲器、全局存儲器,可以顯示這些存儲單元的使用。離核距離近的延遲低,訪存效率高,因此應盡量使用離核近的存儲單元。本文通過下面兩項技術對各并行熱點GPU進行優化(GPU映射設計時已保證訪存對齊):①共享存儲訪問取代全局存儲訪問;②采用寄存器存儲數量較少的中間變量。通過這兩個步驟修改,各熱點均能獲得部分性能提升,效果見表2(優化手段0表示無優化,1采取GPU存儲優化手段1,2在1基礎上采用GPU存儲優化手段2,3在2基礎上增加計算通信重疊優化)。表中數據顯示了本文優化效果。 表2GPU存儲優化技術效果 Fig.2EffectsofstorageoptimizingmethodonGPU ms 最佳維度設計:GPU是眾核架構,細粒度并行,對于線程數量非常敏感,因此需要合理設計線程維度來保證GPU性能發揮。GPU上的線程數量可以是任意的,全部測試是不可能的,需要一套理論指導線程數量的選擇。本文設計了一種線程維度選擇方法,步驟如下: 1)計算kernel的GPU設備占用率(occupancy); 2)選擇占用率最高的幾個線程數量進行實驗測試,擇優選取。 GPU設備占用率是發揮GPU性能的一項重要指標,主要受限于活動的warp數目,而活動的warp數目與使用的寄存器、共享存儲器有關。通過統計kernel函數使用的寄存器數量和共享存儲器容量,可以計算出可活動warp的數量,再根據warp數量與線程數量關系圖,可以初步選定幾個占用率高的線程數量。針對上述選取的線程數量逐一進行實驗測試,對比性能,可得到最佳線程維度。 比如在協方差矩陣計算中,每個thread需要18個寄存器,每個block需要3072byte的共享存儲,對GPU的最大活動warp數量進行分析,通過計算可知,寄存器和共享存儲器的數量都不會限制warp數量;此時,warp數量受最大warp數量限制,與線程數量有關,其關系見圖3。選擇線程數量128,256,512,1024時,活動warp數量達到最大64,occupancy達到100%。再對這4個線程維度進行實驗測試,統計并對比結果數據,獲得最佳線程維度。 圖3 線程數量對warp數量的影響(協方差)Fig.3 Effect between threads and warps(COV) 計算所有GPU并行熱點occupancy,選擇線程數量使得活動warp數量最大化,測試并統計其結果,見表3。表中數據顯示,當線程數量為1024時,白化處理可以獲得最高性能;其他熱點在線程數量為512時性能最佳。 表3 線程數量對性能的影響 4.1 實驗平臺與測試數據 本文用統一計算設備架構(ComputeUnifedDeviceArchitecture,CUDA)技術實現上述GPU并行映射方案和優化策略。其中涉及的矩陣、向量運算均手動實現,未使用cublas庫,主要有以下幾個方面的考慮:1)空間復雜度,cublas庫要求數據類型是float,而高光譜影像數據類型為unsignedchar,如需轉換將增加3倍存儲空間,可能超過GPU全局存儲容量,導致無法處理;2)除開unsignedchar到float類型的轉換開銷,GPU或集成眾核(ManyIntegratedCore,MIC)等協處理器訪問unsignedchar類型的延遲比float類型小很多;3)cublas庫函數任務無法拆分,必須先通信后計算,將導致無法使用計算通信重疊的優化策略;4)由于高光譜數據的特點,矩陣運算不規整,用通用方法優化的cublas未必能獲得更好的效果。 實驗采用當前主流的GPU微型超算平臺,搭載2個8核IntelXeonE5-2650CPU和nVidiaTeslaK20GPU。軟件平臺采用LinuxCentOS6.2操作系統、GCC4.4.6編譯器、CUDA5.0工具包。 本文采用表4羅列的5組機載可見光成像光譜儀(AirborneVisibleInfraredImagingSpectrometer,AVIRIS)高光譜影像數據。數據已經過預處理,把16位int型光譜信息轉換為unsignedchar類型的像素信息。 表4 高光譜影像數據詳細信息 關于ICA迭代次數的約定:由于高光譜影像數據和ICA迭代過程中取得的隨機數不同,ICA迭代次數也將有所差異,不同的迭代次數導致時間消耗不可比。為了較準確地對比算法性能,本文做出如下約定:相同的數據取固定的迭代次數。通過多次實驗取平均值的方法,確定各組數據的迭代次數(見表5)。 表5 高光譜數據迭代次數 4.2 兩種測評基準 本文從最優串行和CPU滿負載并行兩個方面對算法性能進行測評。 1)最優串行程序。表6分別羅列了開啟優化開關O0,O1,O2,O3時,處理高光譜影像數據1的時間。優化開關為O2時,串行程序執行時間最短,作為與并行算法對比的標準。 表6 串行程序優化執行時間表 本文通過對比線程級和進程級并行程序的性能,采取性能較好的CPU并行方案作為CPU滿負載并行標準。本文分別采取OpenMP多線程并行和MPI多進程并行,實現這兩種并行FastICA降維算法,測試性能并比較,見表7。對比表中數據,MPI并行程序能獲得更好的性能,因此本文以MPI并行FastICA程序作為CPU滿負載并行程序。 表7 CPU并行程序加速效果 4.3 GPU對CPU的性能優勢 圖4 各熱點GPU與串行加速比Fig.4 Speed-up between GPU and serial 統計G-FastICA高光譜影像降維算法中各步驟的耗時信息,對比最佳串行程序(見圖4)和MPI并行程序(見圖5)。圖4數據顯示,本文設計的各熱點GPU映射方案能獲得比串行快幾十倍的加速比,其中協方差矩陣計算加速近50倍,白化處理加速300倍左右,ICA迭代過程加速42~109倍不等,IC變換可加速19~41倍。圖5顯示GPU相對CPU在并行計算上更有優勢,本文設計的GPU映射方案比CPU并行版本(MPI)效率更高,其中協方差矩陣計算GPU比CPU快4~6倍,白化處理加速6~8倍,ICA迭代中GPU比CPU快8~11倍,IC變換由于計算量較小,GPU和CPU性能差距不大。 圖5 各熱點GPU與CPU并行加速比Fig.5 Speed-up between GPU and CPU 圖6統計了G-FastICA算法對最佳串行程序、MPI并行程序總時間的加速比。圖中數據顯示,G-FastICA算法比串行FastICA算法加速36~72倍不等;G-FastICA算法比MPI并行算法加速4.1~6.5倍不等。這說明在高光譜影像降維FastICA處理時,CPU/GPU異構系統能比CPU并行系統獲得更好的性能。 圖6 G-FastICA與串行和MPI并行的加速比Fig.6 Speed-up between G-FastICA and serial or MPI 本文研究了高光譜影像降維快速獨立成分分析方法,提出和實現了基于GPU的G-FastICA并行算法,并基于GPU架構對算法進行優化研究。實驗結果顯示了GPU比CPU具有更好的計算優勢,G-FastICA并行算法最高可加速72倍。 通過在CPU/GPU異構系統上研究快速獨立成分分析降維方法,獲得了良好的性能,探討了GPU加速高光譜影像降維的可行性,切實加速了高光譜影像降維過程。本文算法可進一步擴展至GPU集群來提高性能。 References) [1]GreenRO,EastwoodML,SartureCM,etal.Imagingspectroscopyandtheairbornevisible/infraredimagingspectrometer(AVIRIS)[J].RemoteSensingEnviron, 1998, 65(3): 227-248. [2]GreenAA,BermanM,SwitzerP,etal.Atransformationfororderingmultispectraldataintermsofimagequalitywithimplicationsfornoiseremoval[J].IEEETransactiononGeoscienceandRemoteSensing, 2000, 26(1): 65-74. [3]KaarnaA,ZemcikP,K?lvi?inenH,etal.Compressionofmultispectralremotesensingimagesusingclusteringandspectralreduction[J].IEEETransactiononScienceRemoteSensing, 2000, 38(2): 1073-1082. [4]ScottD,ThompsonJ.Probabilitydensityestimationinhigherdimensions[C]//Proceedingsofthe15thSymposiumontheInterfaceComputerScienceandStatistics, 1983: 173-179. [5]JolliffeIT.Principalcomponnentanalvsis[M].USA:Sprinner-Verlan, 1986. [6]Hyv?rinenA,OjaE.Independentcomponentanalysis:algorithmandapplications[J].NeuralNetworks, 2000, 13(4-5): 411-430. [7]TenenbaumJB,DeSilvaV,LangfordJC.Aglobalgeometricframeworkfornonlineardimensionalityreduction[J].Science, 2000, 290(5500): 2319-2323. [8]RoweisST,SaulLK.Nonlineardimensionalityreductionbylocallylinearembedding[J].Science, 2000, 290(5500): 2323-2326. [9]TOP500.TOP500supercomputersites[EB/OL]. (2012-11) [2014-09-26]http://www.top500.org. [10]ValenciaD,LastovetskyA,O′FlynnM,etal.ParallelprocessingofremotelysensedhyperspectralimagesonheterogeneousnetworksofworkstationsusingheteroMPI[J].InternationalJournalofHighPerformanceComputingApplications, 2008, 22(4): 386-407. [11]PlazaJ,PlazaA,PérezR,etal.Parallelclassificationofhyperspectralimagesusingneuralnetworks[J].ComputationalIntelligenceforRemoteSensingStudiesinComputationalIntelligence, 2008, 133: 193-216. [12]SánchezS,RamalhoR,SousaL,etal.Real-timeimplementationofremotelysensedhyperspectralimageunmixingonGPUs[J].JournalofReal-timeImageProcessing, 2012, 32(1): 518-522. [13]YangH,DuQ,ChenGS.Unsupervisedhyperspectralbandselectionusinggraphicsprocessingunits[J].IEEEJournalofSelectedTopicsinAppliedEarthObservationsandRemoteSensing, 2011, 4(3): 660-668. [14]RamalhoR,TomásP,SousaL.EfficientindependentcomponentanalysisonaGPU[C]//Proceedingofthe10thIEEEInternationalConferenceonComputerandInformationTechnology,2010:1128-1133. [15]ForgetteJ,Wachowiak-SmolíkováR,WachowiakM.Implementingindependentcomponentanalysisingeneral-purposeGPUarchitectures[C]//ProceedingsoftheInternationalConferenceonDigitalInformationProcessingandCommunications2011:233-243. [16]HyvrinenA.Fastandrobustfixed-pointalgorithmsforindependentcomponentanalysis[J].IEEETransactionsonNeuralNetworks,1999,10(3):626-634. [17]HyvrinenA.Thefixed-pointalgorithmandmaximumlikelihoodestimationforindependentcomponentanalysis[J].NeuralProcessLett,1999,10(1):1-5. A parallel algorithm of FastICA dimensionality reduction for hyperspectral image on GPU FANG Minquan, ZHOU Haifang, ZHANG Weimin, SHEN Xiaolong Fastindependentcomponentanalysisdimensionalityreductionforhyperspectralimageneedsalargeamountofmatrixanditerativecomputation.Byanalyzinghotspotsofthefastindependentcomponentanalysisalgorithm,suchascovariancematrixcalculation,whiteprocessing,ICAiterationandICtransformation,aGPU-orientedmappingschemeandtheoptimizationstrategybasedonGPU-orientedalgorithmonmemoryaccessingandcomputation-communicationoverlappingwereproposed.Theperformanceimpactofthread-blocksizewasalsoinvestigated.Experimentalresultsshowthatbetterperformancewasobtainedwhendealingwiththehyperspectralimagedimensionalityreductionproblem:theGPU-orientedfastindependentcomponentanalysisalgorithmcanreachaspeedupof72timesthanthesequentialcodeonCPU,anditruns4~6.5timesfasterthanthecasewhenusinga16-coreCPU. graphicprocessingunit;hyperspectralimagedimensionalityreduction;fastindependentcomponentanalysis;parallelalgorithm;performanceoptimization 2014-09-28 國家自然科學基金資助項目(61272146,41375113,41305101) 方民權(1989—),男,浙江東陽人,博士研究生,E-mail:fmq@hpc6.com;周海芳(通信作者),女,教授,博士,碩士生導師,E-mail:haifang_zhou@163.net 10.11887/j.cn.201504011 http://journal.nudt.edu.cn TP A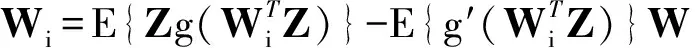
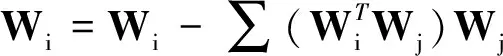
2 FastICA算法并行化研究

3 GPU性能優化

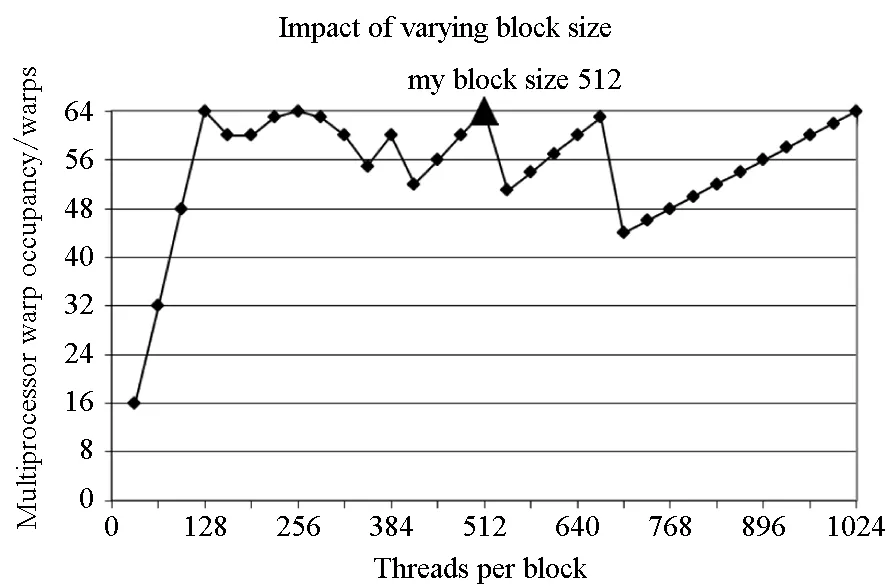
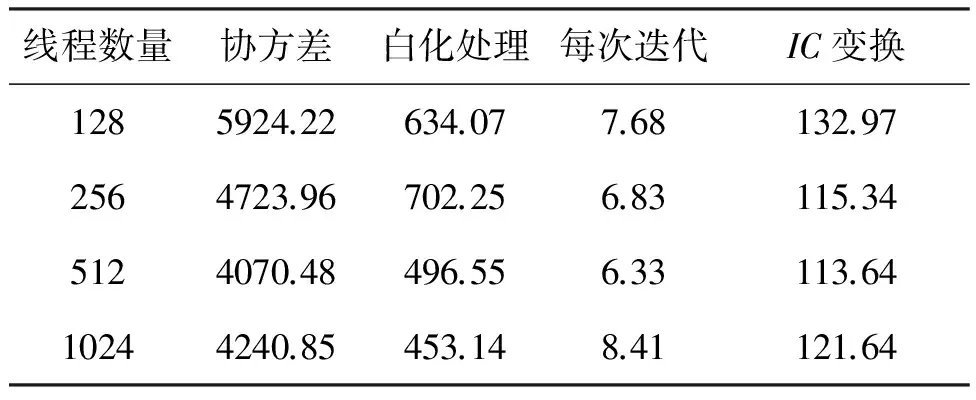
4 實驗結果
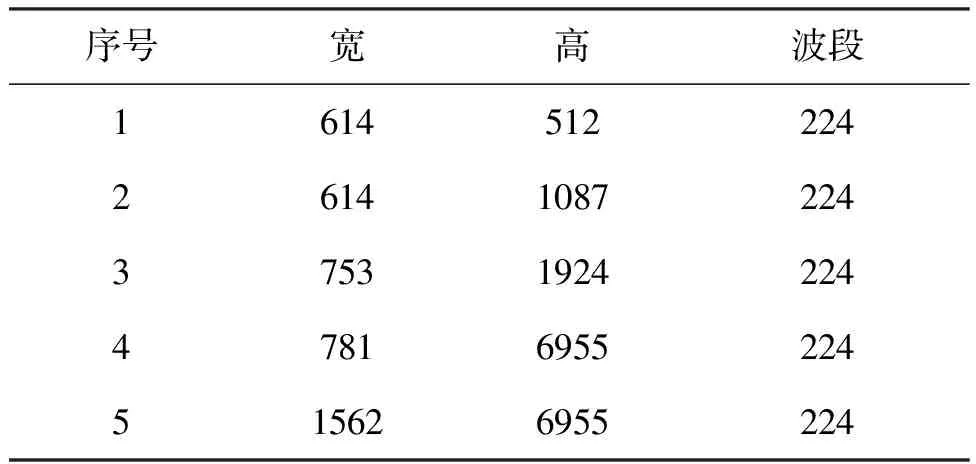



5 結論

