采用狀態轉移矩陣的攔截中段制導方法*

柴 華，仲 明，梁彥剛

采用狀態轉移矩陣的攔截中段制導方法*

柴 華1，仲 明2，梁彥剛1

(1.國防科技大學 航天科學與工程學院， 湖南 長沙 410073；

2.中國人民解放軍69006部隊， 新疆 烏魯木齊 830001)

基于相對運動理論提出攔截中段制導方法。方法原理為，將攔截器初始軌跡與施加修正后的軌跡視為一主一從兩空間目標，以相對運動理論描述從目標相對于主目標的運動規律，于是初始的修正量可由終點處相對狀態求解。給出了一般形式的相對運動模型，運用幾何法與變分法推導得到了J2攝動影響下相對運動的狀態轉移矩陣，在此基礎上，提出了采用狀態轉移矩陣的攔截中段制導方法。仿真算例表明，提出的方法能夠為工程實際中的攔截中段制導提供有效支持。

中段制導；相對運動；J2攝動；狀態轉移矩陣

(1.CollegeofAerospaceScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China;

2.ThePLAUnit69006,Wulumuqi830001,China)

在導彈防御作戰中，中段制導是指攔截器在助推段結束之后、末段導引開始之前，為消除環境噪聲等因素造成的飛行狀態誤差，采用脈沖推力等方式實施一次或多次狀態修正的過程。中段制導的效果好壞直接關系到攔截器能否捕獲目標并在末段導引中占據優勢的攔截幾何，因而具有十分重要的作用[1-3]。脈沖推力式的中段制導事實上可以抽象為一固定時間攔截問題，即給定初、終位置與飛行時間，求解初始需用速度的問題。在二體假設下，求解固定時間攔截問題有許多經典方法，如Herrick方法[4]、Godal方法[4]、Lambert飛行時間定理[5]等。然而，當引入更為精確的引力場模型時，上述方法不再適用，需要探索更為有效的求解方法。

考慮到對于攔截中段制導這一特定的固定時間攔截問題而言，飛行時間較短(約200s)、速度修正量較小(約100m/s)，本文提出基于相對運動理論的求解方法。相對運動理論廣泛地應用于衛星編隊飛行、空間交會對接等領域，涌現出了CW方程、TH方程等經典模型。通過引入三大假設：參考軌道偏心率為0，地球引力為中心引力場，兩目標距離遠小于地心距，Clohessy與Wiltshire[6]將非線性的相對運動模型簡化為便于解析求解的線性時變微分方程組，即CW方程(亦稱Hill[7]方程)。舍棄圓參考軌道假設，Tschauner與Hempel推導得到了適用于橢圓參考軌道的線性相對運動模型，給出了以參考軌道真近點角/偏近點角表示的解析解，其相對運動模型被稱為TH方程。Yamanaka與Ankersen[8]引入變量替換，簡化了TH方程的求解過程，推導了一種形式簡潔的狀態轉移矩陣，并探討了其與CW方程的一致性。盡管CW方程與TH方程在工程實際中得到了廣泛應用，但兩者均以二體中心引力場為前提，因此難以滿足要求。Gim與Alfriend等[9-11]針對J2攝動影響下的相對運動模型展開了研究，避免了直接求解復雜微分方程組，推導給出了相對運動方程的狀態轉移矩陣，為實現高精度的相對運動建模創造了條件。本文將以此狀態轉移矩陣為基礎，提出一種有效的固定時間攔截問題求解策略，并探討其在攔截中段制導中的實用性。

1 坐標系定義

所涉及的坐標系為地心慣性坐標系與當地垂直/當地水平坐標系，兩者定義如下：

地心慣性(EarthCenteredInertial，ECI)坐標系，記為I。 原點OE位于地心，OExI軸在赤道平面內指向平春分點，OEzI軸垂直于赤道平面指向北極，OEyI軸與OExI，OEzI軸垂直并滿足右手定則，如圖1所示。由于歲差與章動影響，春分點具有進動性。在建立地心慣性系時需指定春分點基準。本文采用的ECI系是以2000年1月1日12:00:00的平春分點為基準，因此又稱為J2000坐標系。

當地垂直/當地水平(LocalVerticalLocalHorizontal，LVLH)坐標系，記為L。原點O位于飛行器質心，Ox軸指向飛行器地心矢徑方向，Oy軸在飛行器彈道(軌道)平面內垂直于Ox軸并指向速度方向，Oz軸與Ox，Oy軸垂直并滿足右手定則，如圖1所示。

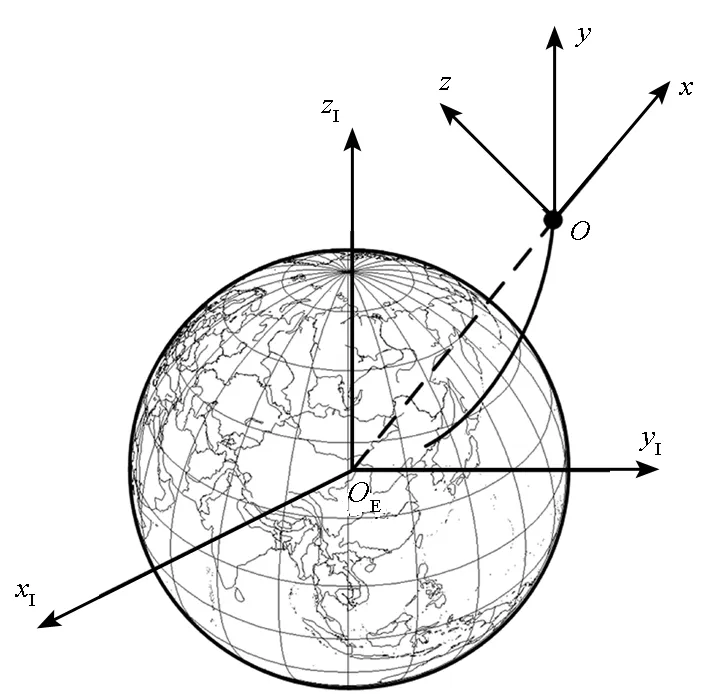
圖1 ECI坐標系與LVLH坐標系Fig.1 ECI coordinate system and LVLH coordinate system

由ECI系到LVLH系的轉換矩陣可由式(1)給出。

MI→L=M3(θ)M1(i)M3(Ω)

(1)

式中，θ=ω+f為飛行器緯度幅角(ω為近地點角距， f為真近點角)，i為軌道傾角，Ω為升交點赤經。

2 相對運動方程

設空間中存在主目標與從目標兩飛行器，兩者在ECI系下的位置矢量分別為Rc與Rd，由經典軌道力學可知

(2)

式中，μ為地球引力常數，fc與fd分別為兩目標所受攝動力產生的加速度。

將從目標相對于主目標的位置矢量記作r=Rd-Rc，那么有

式中，f=fd-fc為兩目標攝動加速度之差。

以主目標LVLH系作為基準坐標系，記作LC。式(3)在LC系中描述需要考慮絕對導數與相對導數的相互轉換，即

(4)

結合式(3)、式(4)可得

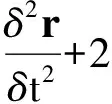
(5)

式(5)即為LC系下一般形式的相對運動方程。對應于不同的引力場模型，該方程具有不同的表現形式，其解析求解是十分困難的。在二體引力場假設下，可將式(5)線性化(即TH方程)，并推導給出形式簡潔的狀態轉移矩陣，相關研究已經較為成熟。當考慮更為精確的引力場模型時，問題變得更加復雜。Alfriend等學者對這一問題進行了研究，推導了J2攝動影響下相對運動的狀態轉移矩陣。

3 狀態轉移矩陣

為避免直接求解微分方程帶來的困難，Alfriend等學者采用幾何法來推導相對運動方程的狀態轉移矩陣。該方法的主要思路為，將從目標相對于主目標的位置速度轉換為軌道根數之差，以軌道根數之差隨時間的變化來刻畫相對狀態的遷移。在推導過程中，需引入差分軌道根數的概念。首先給出兩組相互等價的軌道根數：

(6)

式中：eCL為經典軌道根數，a為半長軸，e為偏心率；eNS為非奇異軌道根數，q1=ecosω，q2=esinω。為避免經典軌道根數在描述圓軌道時出現的奇異現象，下文將采用非奇異軌道根數實現狀態轉移矩陣的推導。

差分軌道根數定義為從目標與主目標軌道根數之差，即

δe=ed-ec

=[δa,δθ,δi,δq1,δq2,δΩ]T

(7)

式中，下標d與c分別表示從目標與主目標。需要指出，在下文推導中，所有不含下標c的軌道根數(或其衍生項)均對應于主目標。例如，式(8)中的R等價于式(2)中的Rc。

3.1 由相對位置速度到差分密切軌道根數的轉換

以LC系作為基準坐標系，主目標地心矢徑與速度矢量可分別表示為

(8)

從目標地心矢徑與速度矢量可分別表示為

(9)

式中：x，y，z分別為從目標相對位置矢量r在LC系三方向的分量；?x，?y與?z分別為主目標角速度矢量在LC系三方向的分量，即

?c=[?x,?y,?z]T

(10)

與此同時，從目標滿足式(11)所示關系。

(11)

式(1)已經給出了ECI系與LVLH系之間的轉換關系，考慮到主目標與從目標的軌道根數足夠接近，可將矩陣MLD→I在MLC→I處泰勒展開且僅保留一階項，結合式(8)、式(9)有

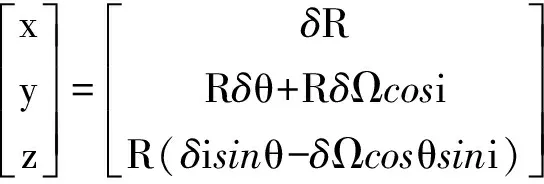
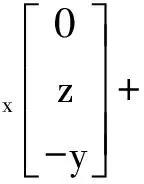
(12)

由軌道力學可知

(13)

(14)

(15)

將式(13)～(15)代入式(12)，可將LC系下從目標的相對狀態表示為差分軌道根數的形式。于是有

(16)

3.2 由差分密切軌道根數到差分平均軌道根數的轉換

在J2攝動影響下，密切軌道根數隨時間的變化較為復雜，難以給出解析描述。因此，在推導軌道根數之差的時間遷移規律時，采用平均軌道根數作為替代對象。本節將推導給出差分密切軌道根數與差分平均軌道根數之間的轉換關系。

許多文獻對密切軌道根數與平均軌道根數的轉換問題進行了研究，此處采用文獻[10]的方法，即有

(17)

式中，e為密切軌道根數，em為平均軌道根數，elp為長周期項，esp1與esp2為短周期項。需要指出的是，elp，esp1與esp2均以平均軌道根數表示，也就是說，由密切軌道根數計算平均軌道根數需通過迭代來實現。下文將在4.1節對這一問題進行詳細闡述。

由式(17)可知

(18)

式中，I為單位矩陣。

于是有

δe(t)=D(t)δem(t)

(19)

3.3 差分平均軌道根數的時間遷移

與密切軌道根數相比，平均軌道根數的變化規律更為簡潔，有

(20)

式中，上標m表示平均根數，下標0表示初始時刻，M為平近點角，λ=M+ω為平緯度幅角。ωm，Mm與Ωm的時間變化率均可由初始時刻的平均軌道根數表示。

對式(20)中最后一式等號兩邊進行變分操作，保留一階項，有

(21)

式中，Δt=t-t0。

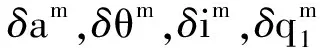
δem(t)=Φe(t,t0)δem(t0)

(22)

結合式(16)、式(19)、式(22)，可以得到J2假設下相對運動方程的狀態轉移矩陣，即

(23)

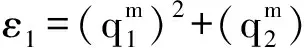
4 攔截中段制導方法

4.1 平均軌道根數的計算

式(17)給出了密切軌道根數與平均軌道根數之間的關系，依據該式計算平均軌道根數需要通過迭代來實現。迭代步驟如下：

(24)

4) 重復上述過程，直到滿足收斂準則為止。收斂準則可取為

(25)

式中，ε為容許誤差限。

4.2 制導方法流程

前文指出，攔截中段制導問題事實上可以抽象為固定時間攔截問題。考慮到對于中段制導而言，飛行時間較短而速度修正量較小，因而本文提出基于狀態轉移矩陣的制導方法。

問題描述：

在ECI坐標系下，已知t0時刻攔截器的位置、速度矢量分別為R0，V0，預測命中時刻為tf，預測命中點為Rf。 由于誤差因素的影響，攔截器以初始狀態難以準確到達預測命中點，需要實施中段導引，確定速度修正量Δv。

方法流程：

1)由初始狀態R0、V0計算初始時刻的密切軌道根數es，建立初始的LVLH坐標系；

4) 計算終點LVLH系下預測命中點的相對位置rf，即

(26)

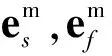
6)初始時刻的速度修正量Δv滿足

(27)

由式(27)可知

(28)

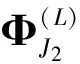
圖2 制導方法流程

Fig.2Procedureofthemidcourseguidancemethod

5 仿真算例

上文提出了采用狀態轉移矩陣的攔截中段制導方法。本節將引入仿真算例，驗證所提方法的性能，分析其適用條件。

5.1 狀態轉移矩陣的精度

首先考察本文給出的狀態轉移矩陣在刻畫攔截器相對運動時的精度。設t0=1003.6s時刻攔截器在J2000系下的位置速度矢量分別為

R0=[2 196 308.118, -2 361 659.419, 6 082 688.107]T；V0=[853.466 678，-6 083.398 166，2 767.032 528]T。

在t0時刻向攔截器施加速度沖量，攔截器的飛行軌跡將發生變化。表1給出了LVLH系下3組不同的速度沖量值。以解析的J2軌跡外推結果作為真值，將偏離真值的程度作為衡量狀態轉移矩陣精度的指標。圖3給出了不同速度沖量下狀態轉移矩陣的誤差隨時間的變化情況。

表1 LVLH系下的初始速度沖量

圖3 狀態轉移矩陣的誤差隨時間的變化Fig.3 Error of state transition matrix versus time

由圖3可知，在本文給出的仿真條件下(時間不超過200s、速度修正量不大于100m/s)，采用狀態轉移矩陣刻畫攔截器的飛行軌跡具有較高的精度：與真值相比，位置誤差不超過300m，速度誤差不超過0.4m/s。需要注意的是，在圖3中，隨著速度沖量的增加，狀態轉移矩陣的性能出現下降。這是由于當速度沖量增加時，新軌道與參考軌道的偏差在增大，推導狀態轉移矩陣時引入的小偏差假設受到挑戰，忽略非線性項的代價越來越明顯地體現出來。

5.2 中段制導方法的性能

設預測命中時刻tf=1186.9s，預測命中點在J2000系下的位置矢量為

Rf=[2 322 135.847, -3 439 448.051, 6 478 344.336]T。

采用兩種方法求解初始時刻所需的速度修正量Δv。 一種是圖2給出的中段制導方法，一種是文獻[5]給出的基于Lambert飛行時間定理的聯合方程方法。將兩種方法求解得到的速度修正量施加至攔截器，得到預測命中時刻攔截器與Rf點的距離Δr作為衡量制導方法精度的指標。仿真結果如表2所示，表2同時還給出了兩種方法的計算耗時Δt。

表2 制導方法性能對比

由表2可知，由于考慮了J2項攝動的影響，本文提出的中段制導方法比聯合方程方法更加精確。本文方法的計算耗時約為20ms，盡管比聯合方程方法高出一個量級，但是仍處于可接受的范圍內。

5.3 中段制導方法的適用性

需要指出，本文采用線性化的相對運動模型來實現攔截中段制導，這決定了制導方法的性能與Δv的大小密切相關(即主從目標是否足夠接近從而滿足線性化條件)。改變預測命中點Rf的位置，圖4給出了需用速度修正量Δv與方法誤差Δr的對應關系，以此考察制導方法的適用性。由圖可知，隨著Δv的增加，方法誤差Δr也不斷增大。當Δv達到100m/s時，制導方法產生的Δr不超過200m，考慮到攔截器末制導段的修正能力，這一誤差量級是足夠精確的。

圖4 Δr與Δv的對應關系Fig.4 The relations between Δr and Δv

6 結論

對攔截中段制導問題展開了研究。針對高精度引力場模型條件下固定時間攔截問題難以求解的現狀，提出了基于相對運動模型的求解策略。在J2引力場假設下，推導得到了相對運動的狀態轉移矩陣，從而可將固定時間攔截問題轉化為相對狀態的轉移問題。仿真算例表明，提出的方法為快速求解速度修正量提供了一條有效途徑。

由于推導過程引入了線性化，因此本文的制導方法僅適用于攔截器實際飛行軌跡與標稱飛行軌跡足夠接近的情形。但仿真算例分析表明，這一約束并不影響本文方法在攔截中段制導中的應用。

References)

[1]ZarchanP.Tacticalandstrategicmissileguidance[M]. 4thed.USA:AmericanInstituteofAeronauticsandAstronautics, 2002.

[2]ZarchanP.Midcourseguidancestrategiesforexoatmosphericintercept[R].CharlesStarkDraperLaboratory, 1998.

[3]NewmanB.Strategicinterceptmidcourseguidanceusingmodifiedzeroeffortmisssteering[J].JournalofGuidance,Control,andDynamics, 1996, 19(1): 107-112.

[4] 任萱. 人造地球衛星軌道力學 [M]. 長沙: 國防科技大學出版社, 1988.RENXuan.Orbitalmechanicsofartificialearthsatellite[M].Changsha:NationalUniversityofDefenseTechnologyPress, 1988.(inChinese)

[5]BattinRH.Anintroductiontothemathematicsandmethodsofastrodynamics[M].USA:AmericanInstituteofAeronauticsandAstronautics, 1999.

[6]ClohessyWH,WiltshireRS.Terminalguidancesystemforsatelliterendezvous[J].JournaloftheAerospaceScience, 1960, 27(9): 653-658.

[7]HillGW.Researchesinthelunartheory[J].AmericanJournalofMathematics, 1878, 1(3): 245-260.

[8]YamanakaK,AnkersenF.Newstatetransitionmatrixforrelativemotiononanarbitraryellipticalorbit[J].JournalofGuidance,Control,andDynamics, 2002, 25(1): 60-66.

[9]AlfriendKT,SchaubH,GimDW.Gravitationalperturbations,nonlinearityandcircularorbitassumptioneffectsonformationflyingcontrolstrategies[J].AdvancesintheAstronauticalSciences, 2000, 104: 139-158.

[10]GimDW,AlfriendKT.Statetransitionmatrixofrelativemotionfortheperturbednoncircularreferenceorbit[J].JournalofGuidance,Control,andDynamics, 2003, 26(6): 956-971.

[11]AlfriendKT,VadaliSR,GurfilP,etal.Spacecraftformationflying:dynamics,controlandnavigation[M].USA:Butterworth-Heinemann, 2009.

Midcourse guidance of interception using state transition matrix

CHAI Hua1, ZHONG Ming2, LIANG Yangang1

Onthebasisofrelativemotiontheory,amidcourseguidancemethodofexoatmosphericinterceptionwasdeveloped.Themechanismofthismethodisthattreatingtheinitialandmodifiedtrajectoriesaschiefanddeputyspaceobjectsrespectively,modelingthedynamicsofthedeputyrelativetothechiefbytherelativemotiontheoryandsolvingtheinitialcorrectionsthroughthefinalrelativestates.TheuniversalrelativemotionmodelwasprovidedandthenthestatetransitionmatrixofrelativemotionundertheinfluenceofJ2disturbancewasderivedbyemployingthegeometryandthevariationmethod.Lastlythemidcourseguidancemethodusingstatetransitionmatrixwasproposedonthisbasis.Simulationexampleshowsthattheproposedmethodservesasanefficientsupportformidcourseguidanceofinterceptorsinpractice.

midcourseguidance;relativemotion;J2disturbance;statetransitionmatrix

2015-06-10

國家自然科學基金資助項目(11272346)作者簡介：柴華(1988—)，男，山西沁水人，博士研究生，E-mail:chaihua@nudt.edu.cn；梁彥剛(通信作者)，男，副教授，博士，E-mail：liangyg@nudt.edu.cn

10.11887/j.cn.201504023

http://journal.nudt.edu.cn

文獻標志碼： 文章編號：1001-2486(2015)04-137-06