基于小波消噪與關聯維數的經穴電位信號研究

李 江，王曉倩

（浙江大學控制科學與工程系，杭州310027）

基于小波消噪與關聯維數的經穴電位信號研究

李 江，王曉倩

（浙江大學控制科學與工程系，杭州310027）

穴位點在中醫鄰域具有相對于非穴位點的特殊治療效果。為此，提出一種基于小波去噪和關聯維數的經穴電位信號分析方法。采集大陵、曲澤和尺澤3個穴位點及其附近的非穴位點電位信號，小波去噪后進行混沌特征分析，求取關聯維數和最大李雅普諾夫指數，觀察穴位點和非穴位點特征差異。實驗結果表明，穴位點電位的關聯維數高于其附近非穴位點電位的關聯維數。

小波；混沌；非線性；經穴電位；關聯維數；最大李雅普諾夫指數

1 概述

中醫學經過數千年的研究發展，已經取得了很大的成就，引起了世界各國醫學研究者的重視。然而，傳統醫學在經絡穴位上的研究目前還缺少嚴謹的科學論證，對人體經絡穴位的本質特征還需要進一步探索。一般認為，穴位是人體具有生物活性的點［1］，經絡是來源于人體內部的各個器官的電磁能量的傳輸通道［2］。穴位點與其周邊的非穴位區域相比，通常被認為具有不一樣的電特性，如具有高電位、低阻抗、高電容［3］等特性。由于依賴于一定的電刺激的阻抗測量容易表現出很高的混雜性及較強的隨機性，本文選擇重復性更好的穴位電位信號分析。

目前對經穴電位的分析研究主要集中在線性分析，通過在時域和頻域對信號提取特征量進行研究。研究表明，大多數生物電信號都存在一定的混沌非線性特征，例如腦電、心率、血壓等［4］。非線性混沌信號分析技術可以提取到一些線性分析方法無法得到的特征量，對復雜系統的分析具有重要意義。

由于體表電信號非常微弱，測量過程中容易引入噪聲，特別是工頻干擾［4］。為了得到精確的混沌參數，必須有效地去除信號中的噪聲。傳統的降噪大多集中在信號的時、頻域分析上，而對于穴位電位等生物電信號具有較強的局限性。近年來，隨著小波變換技術的發展，國內外許多研究者將小波分析用于生物醫學信號的提取和去噪，該方法被證明可以有效去除混沌信號中的噪聲，保留大部分的有效信息。本文采集到信號后，先進行小波去噪處理，然后對去噪后的信號進行混沌非線性分析，利用相重構、關聯維數和最大李雅普諾夫指數來表征系統的混沌特征。

2 經穴電位信號的非線性分析

2.1 小波去噪原理

假設含有噪聲的信號χ（t）=s（t）+w（t），其中，s（t）為真實信號；w（t）為噪聲。為了復原信號χ（t），對信號χ（t）進行離散小波變換，其系數可以表示為：

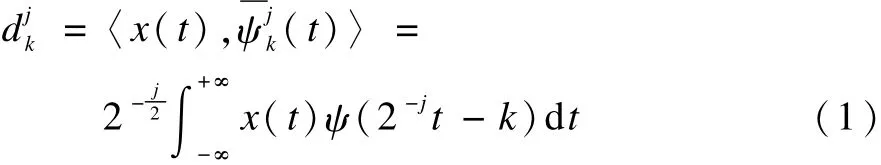
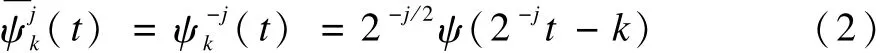
其中，j為尺度，表示小波周期長度；K為時間因子，反映小波在時間上的平移。由于小波變換為線性變換，χ（t）經小波變換后系數為：

對于均值為0、方差為σ2的白噪聲，小波系數的平均功率與尺度成反比，其幅度隨著小波分解層數增加而不斷減小，其能量分散于大量的小波系數上，且白噪聲的小波系數仍是白噪聲［7］。有用信號經小波變換后，其能量被壓縮到相對較少而數值較大的小波系數上。因此，可以在各個尺度上設定閾值，小于該閾值的小波系數置為0，對經過閾值處理的小波系數進行重構，即可完成去噪，得到重構的信號)χ。小波閾值去噪法具有計算量小、濾波效果好的優點，但去噪的穩定性依賴于待消信號，不同的信號可能需要設置不同的閾值［8］。

2.2 相空間重構

相空間重構在混沌時間序列分析中有著重要的意義。這一方法是由Takens提出的，其主要目的是通過單一的系統輸出時間序列來構造一組表征原系統動力學特征的坐標分量，從而近似恢復系統的混沌吸引子。對一個人體經穴信號ν（t），雖然影響其

輸出的變量是未知的，但是可以通過引入延遲時間τ和嵌入維數m，構造一個m維的狀態向量，其重構相空間Y可以表示為：

延遲時間τ和嵌入維數m的選取對相空間的重構質量有著重大的影響。Takens已經證明，對于一個維數為d的吸引子，當嵌入維數m≥2d+1時，重構的吸引子能保持原來吸引子的拓撲特性［9］。但由于d在一個未知的動力學系統中是未知的，因此如何確定m也具有重要意義。本文分別采用互信息法和CAO方法求τ和m。

2.3 延遲時間的確定

互信息函數是2個變量總體依賴性的度量。假設有兩系統Q和S，則互信息的定義為：

I（Q，S）=H（Q）+H（S）-H（Q，S）（5）

其中，H（Q），H（S）為Q，S系統的熵；H（Q，S）為Q，S系統的聯合熵。假設電位序列ν（t）為S，時間延遲τ的數據序列ν（t+τ）為Q，那么理論上的互信息計算式為：

其中，Psq（si，qj）聯合分布概率；Ps（si），Pq（qj）為邊緣分布概率。實際上可以采用等間距劃分空間格子的方法來計算互信息，當互信息第一次達到極小值時，對應的時間即為延遲時間τ。

2.4 嵌入維數的求取

CAO方法是一種改進的偽最近鄰法，可以確定最佳的嵌入維數。其原理如下所述：

在d維空間中，每一個相點矢量X（i），都有一個某距離內的最近鄰點，其距離為當相空間的維數增加到d+1維時，這2個相點的距離就會發生變化，設為，則：

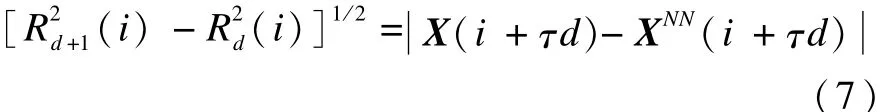
如果鄰近點是真實的，則兩點之間的距離不隨d的增加而變化。定義下式：

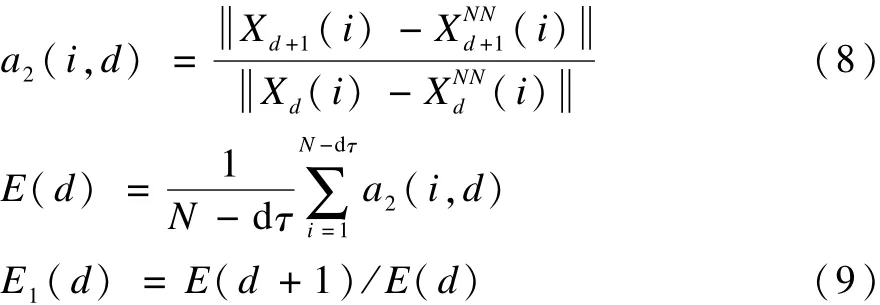
如果時間序列是確定的，那么當d大于某一確定值后，E1（d）將不再變化［10］。

2.5 最大李雅普諾夫指數

混沌運動的基本特點是運動對初值條件極為敏感。2個很靠近的初值所產生的軌道，隨時間推移按指數方式分離，Lyapunov指數就是定量描述這一現象的量［11］。對于一個系統，若有一個Lyapunov指數為正，那么該吸引子對初始條件是極為敏感的，從而在短暫的時間過后變得混沌。對于一維動力系統χn+1=f（χn），設平均每次迭代所引起的指數分離中的指數為λ，于是原來相距為ε的兩點經過n次迭代后相距為：

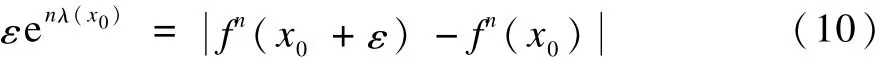
取極限ε→0，n→∞，則上述表達式可以近似為：

其中，λ即為李雅普諾夫指數，對m維的重構相空間，求取所有的李雅普諾夫指數，判斷最大李雅普諾夫指數的正負性，最大李雅普諾夫指數越大，混沌指數越高。

2.6 關聯維數

關聯維數是混動動力系統奇怪吸引子的度量屬性，能夠在一定程度上反映時間序列在各個時刻的相關性程度的變化率。關聯維數越大，表示系統的復雜性越高［12］。對m維重構向量子空間計算關聯積分：

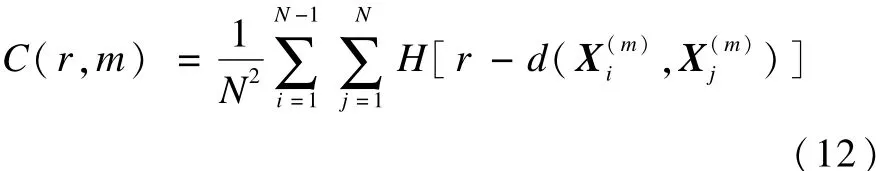
關聯維數為：

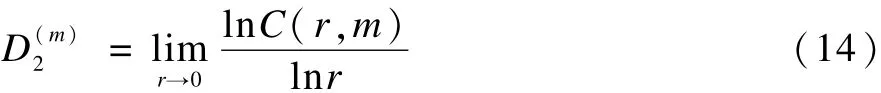
3 實驗數據的采集

3.1 樣本

本文的樣本來自于6位年齡在20歲～25歲之間的健康志愿者，采集手部大陵、曲澤和尺澤3個穴位點以及距離穴位點2 cm處的非穴位點電位作為處理信號。

3.2 儀器

選用南京美易科技有限公司生產的M edlab-U/ 501H生物信號采集處理系統作為實驗儀器設備。M edLab-U/501H的主要相關參數如下：16位A/D采樣，采樣速率最高500 kHz；輸入方式為雙端差分輸入；輸入阻抗為10 MΩ；增益準確度0.5%，增益穩定度0.05%；線性度為滿度的0.1%；噪聲小于2μVRMS；共模抑制比大于110 dB，能夠滿足實驗數據采集要求。

3.3 實驗設計與處理

本課題采用直徑為10 mm的Ag-Agcl表面電極，它的極化電壓很小，能很快穩定下來，有利用生物電信號的檢測［5］。選取大陵、曲澤、尺澤3個穴位點以及它們附近2 cm左右的3個非穴位點進行測量，參考點選用承山穴。預先開啟50 Hz陷波和100 Hz以上濾波功能，放大倍數1 000倍，采集頻率為1 000 Hz，每個測試點采集4組時長為10 s～15 s的數據，一共獲得144個樣本。測量前，在測量點用酒精消毒，并且抹上生理鹽水以增強導電性。

采集到的電位信號與皮膚表面的濕度、電極壓力以及一些其他未知因素有關。為了減小測試環境對數據的影響，本文實驗的具體環境為：溫度28℃，時間13：30-16：30。被測者靜坐姿勢，手臂放松。

穴位電位信號作為一種時變的、非平穩信號，不同時刻有不同的頻率成分。單純的時、頻分析方法是通過傅氏變換聯系起來的，噪聲與信號的區分通過信號的時不變特性或統計特性平穩為前提，且無法同時滿足時域和頻域的分辨率要求。為了能夠更好地反映穴位電位信號的本質，選擇兼具時頻高分辨率的小波變換進行消噪［6］。

4 實驗結果及分析

本文分析的是由人體中醫穴位點及其周圍非穴位點電位信號構成的一維時間序列。原始信號在采集的過程中預先開啟50 Hz陷波處理和100 Hz以上濾波處理。此后對采集信號進行小波軟閾值去噪，最后利用非線性動態分析方法提取出穴位信號的非線性特征。

4.1 小波去噪結果

Matlab環境下，使用小波工具箱的w den函數，采用啟發式閾值形式（Heursure）的軟閾值小波去噪方法對其進行去噪。Heursure形式是sqtwolog形式rigrsure形式的結合，針對各不同尺度的子空間使用不同的閾值進行軟閾值去噪，以取得更加合理、平滑和理想的結果。由于目前對于小波基和分解尺度的選擇沒有統一的理論方法［13］，分別選擇不同的小波基和分解尺度進行實驗，對去噪效果進行比較，選用高消失矩的db8小波，進行10級分解及去噪。原始信號和去噪后的信號如圖1、圖2所示，由圖2可見，經小波處理后的電位信號較原始信號平滑，噪聲大大降低。

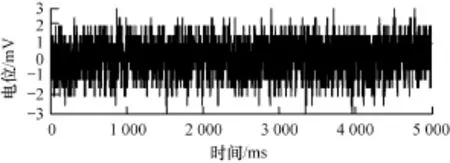
圖1 穴位點原始電位信號

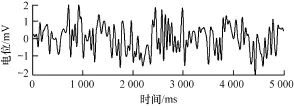
圖2 去噪后的穴位電位信號

4.2 經穴電位信號相空間重構

本文采用互信息法求取經穴電位信號的延遲時間，結果如圖3所示，從圖中可以看出，當延遲時間為17 m s時，互信息第一次達到最小值。從圖4中可以看出該序列的嵌入維數為3。

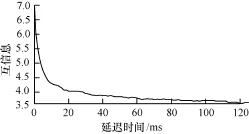
圖3 互信息法求取的延遲時間

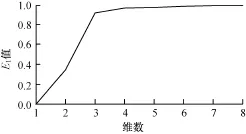
圖4 CAO方法求取的嵌入維數

分別根據互信息法和CAO方法求得最佳的嵌入維數構造出相空間，圖5展示了人體經穴信號在重構相空間中的吸引子。圖中的軌跡既不是孤立點和封閉曲線，也不是隨機分布的范圍，表示經穴電位信號吸引子是一種特殊結構的奇怪吸引子。所以經穴電位信號有可能是混沌的。

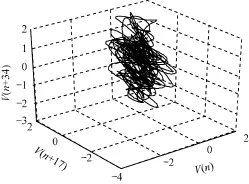
圖5 經穴電位信號的重構相空間（τ=17，m=3）

4.3 最大LyaPunov指數和關聯維數計算

選取采集到的人體穴位點和其附近非穴位點的電位信號，進行關聯維數的計算。嵌入維數取為m= 1～6，計算出關聯積分ln C（r），然后做出ln C（r）對ln（r）的分布圖，如圖6所示，從上到下的曲線為m= 1，2，…，6。用最小二乘法對分布圖進行線性擬合，得到其斜率即為關聯維數，從圖中可以看出存在一段接近平行的線性區域，計算得到此序列的關聯維數為1.6。計算電位信號序列的Lyapnov指數，如圖7所示，根據最小二乘法擬合出的直線斜率即為最大的Lyapnov指數0.028 2。穴位點和其附近的非穴位點電位信號均存在分形維數和正的最大Lyapnov指數，所以都存在混沌非線性特性，可以采用混沌理論來分析。

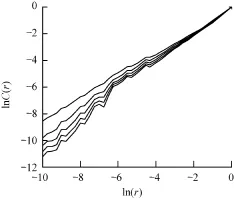
圖6 經穴電位信號的關聯維數

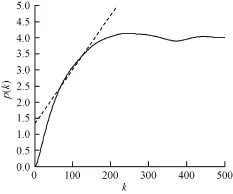
圖7 經穴電位信號的最大LyaPunov指數

4.4 經穴電位信號混沌參數的統計結果

表1顯示了測試者3的6個被測點的混沌參數統計結果。其中，τ，m，D2，LLE分別表示延遲時間、嵌入維數、關聯維數和最大李雅普諾夫指數。可以看出被測信號的李雅普諾夫指數均大于0，說明被測信號具有混沌特性，可以用非線性方法來分析。穴位點和非穴位點的關聯維數存在明顯差異，穴位點的關聯維數大于非穴位點的關聯維數，說明穴位點電位信號的復雜性更高。圖8顯示了測試者1大陵穴的4次實驗得出的D2，雖然不同時間段D2的值有所波動，但是每次實驗獲得的數據中都是大陵穴處的D2比較大，較好地驗證了實驗的重復性。圖9顯示了所有實驗對象各個測試點電位時的平均關聯維數折線圖，每條曲線對應一個測試者。圖10顯示了每個測試點不同對象的平均D2。可以看出，除了測試者3的大陵穴2組D2接近外，其余數據中，每個對象的穴位點關聯維數都明顯大于參照數據。由于大陵穴附近的穴位比較集中，造成了個別數據的反常。雖然個體之間也存在差異，但是穴位電位信號關聯維數的分布區間和非穴位信號有明顯的區別。因此，關聯維數可以作為穴位和非穴位電位信號的分類特征。

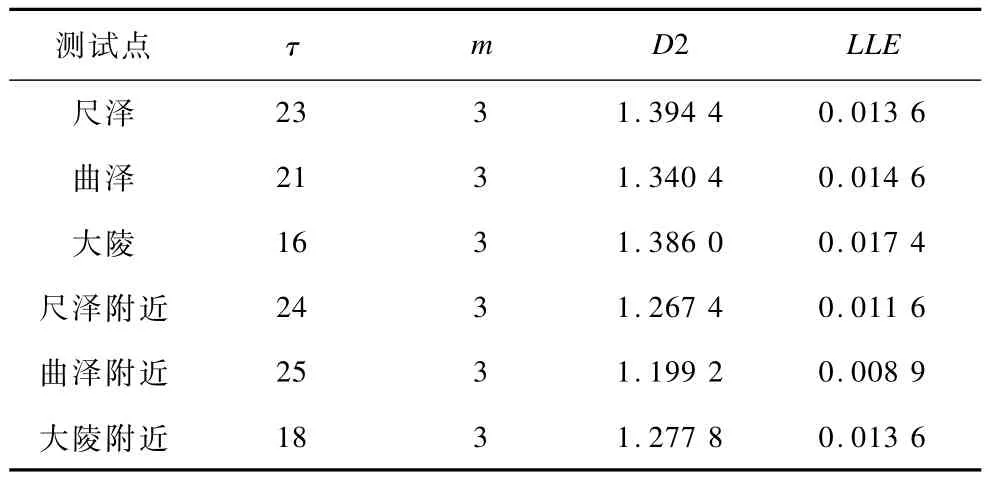
表1 穴位和非穴位點的混沌參數

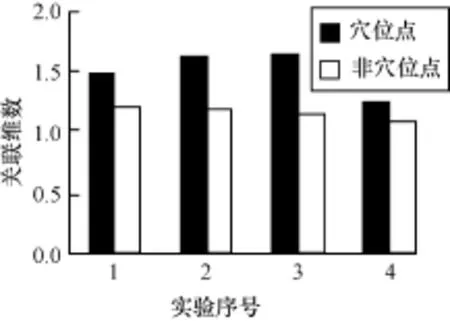
圖8 1個被測對象的關聯維數

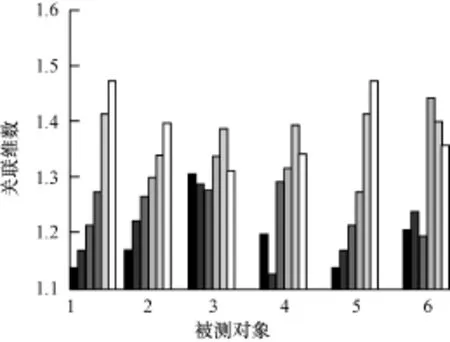
圖9 6個測試者的關聯維數

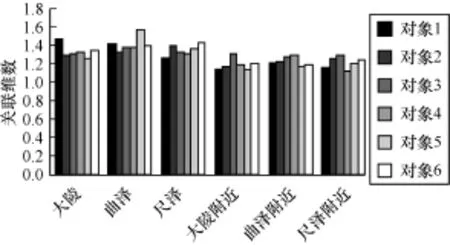
圖10 6個測試點的關聯維數

5 結束語

為驗證中醫穴位理論的科學性，本文進行了體表電位信號的采集和分析實驗。對實驗數據進行歸一化和小波去噪預處理，采用非線性分析方法對預處理后的數據求取混沌參數，結果表明非線性方法相比傳統的線性方法對個體差異的魯棒性更高。每個被測對象的穴位點電位的關聯維數明顯大于其非穴位參考點的關聯維數。根據混沌理論可知，穴位電位信號具有更高的復雜性，初步驗證了中醫理論中穴位學說的科學性。后期將對經絡的傳輸特性進行研究，并實現經絡穴位點的分類，與中醫理論結合實現部分疾病的診斷和預測。

［1］ Ahn A C.Electrical Characterization of Acupuncture Points：Technical Issues and Challenges［J］.Journal of Alternative and Com plementary Medicine，2007，I3（8）：817-824.

［2］ Yung Kaung-Ti.A Bridge Model for Chinese Meridian System Part 2：The Meridian System as a Bridge Resonator［J］.The American Journal of Chinese Medicine，2004，32（6）：985-997.

［3］ Reichmanis M，Marino A A，Becker R O.Laplace Plane Analysis of Impedance Between Acupuncture Points H-3 and H-4［J］.Comparative Medicine East&W est，1977，5（3/4）：289-295.

［4］ 邱天爽，唐 洪，劉海龍.統計信號處理：醫學信號分析與處理［M］.北京：科學出版社，2012.

［5］ Ahn A C，Martinsen O.Electrical Characterization of Acupuncture Points：Technical Issues and Challenges［J］. Journal of Alternative and Complementary Medicine，2007，13（8）：817-824.

［6］ 王巧蘭.微弱生物電信號的提取方法及其應用研究［D］.重慶：重慶大學，2006.

［7］ Vázquez R R，Vélez-Pérez H，Ranta R，et al.Blind Source Separation，Wavelet Denoising and Discriminant Analysis for EEG Artefacts and Noise Cancelling［J］. Biomedical Signal Processing and Control，2012，7（4）：389-400.

［8］ 鐘建軍，宋 健，由長喜，等.基于信噪比評價的閾值優選小波去噪法［J］.清華大學學報：自然科學版，2014，54（2）：259-263.

［9］ 呂金虎，陸君安，陳士華.混沌時間序列分析及應用［M］.武漢：武漢大學出版社，2002.

［10］ Zhang Shuqing，Jia Jian，Gao M in，et al.Study on the Parameters Determination for Reconstruction Phasespace in Chaos Time Series［J］.Acta Physica Sinica，2010，59（3）：1576-1582.

［11］ 楊永鋒，仵敏娟，高 喆，等.小數據量法計算最大Lyapunov指數的參數選擇［J］.振動、測試與診斷，2012，32（3）：371-374.

［12］ Y1lm az D，Güler N F.Analysis of the Doppler Signals Using Largest Lyapunov Exponent and Correlation Dimension in Healthy and Stenosed Internal Carotid Artery Patients［J］.Digital Signal Processing，2010，20（3）：817-824.

［13］ 秦永寬，黃聲享，趙 卿.基于小波消噪和LS-SVM的混沌時間序列預測模型及應用［J］.大地測量與地球動力學，2008，28（6）：96-100.

編輯 顧逸斐

Research on Meridian Potential Signal Based on Wavelet De-noising and Correlation Dimension

LI Jiang，WANG Xiaoqian
（Department of Control Science and Engineering，Zhejiang University，Hangzhou 310027，China）

Considering the issue of acupuncture theory is quetioned regardless of acupoints' efficacy compared with the non-acupoints，a method for meridian potential signal analysis based on wavelet de-noising and correlation demension is presented.Potential signals of PC7，PC3，LU5 and non-acupuncture points near them are sampled，denoising the sampled signals with the help of wavelet.Chaotic features analysis method is taken，which calculates the correlation dimension and the largest Lyapunov exponent.By comparing the chaotic parameters，the potential differences between acupuncture points and non-acupuncture points w ill be identified.Data analysis show s correlation dimension of acupuncture point potential is higher than that of the non-acupuncture points.

wavelet；chaotic；nonlinear；meridian potential；correlation dimension；largest Lyapunov exponent

李 江，王曉倩.基于小波消噪與關聯維數的經穴電位信號研究［J］.計算機工程，2015，41（9）：276-280.

英文引用格式：Li Jiang，Wang Xiaoqian.Research on Meridian Potential Signal Based on Wavelet De-noising and Correlation Dimension［J］.Computer Engineering，2015，41（9）：276-280.

1000-3428（2015）09-0276-05

A

TN911.72

10.3969/j.issn.1000-3428.2015.09.051

李 江（1973-），男，副教授、博士，主研方向：醫學信號非線性分析，控制系統應用；王曉倩，碩士。

2014-09-22

2014-10-24 E-m ail：w xq432@sina.com