低溫邊界條件下柱型凝固問題的數值研究
曲良輝 邢 琳 錢德亮 令 鋒
低溫邊界條件下柱型凝固問題的數值研究
曲良輝 邢 琳 錢德亮 令 鋒
通過考慮移動邊界每次向外推進固定距離時所需要的時間,構造定空間步長方法求解了兩種不同低溫邊界條件下的向外柱型凝固問題,數值模擬了相變過程中移動邊界的運動及介質內溫度場的變化。數值結果表明采用定空間步長方法求解柱型凝固問題是數值穩定的,并且具有較高的精度,對于Stefan問題的研究具有重要的參考價值。
Stefan問題也稱為移動邊界問題,其特點是區域內存在著一個隨時間運動的邊界,如冰的融化、金屬鑄件的凝固、微粒擴散和種群繁衍等。求解Stefan問題,由于問題的非線性性質和移動邊界的未知位置,只有一些特殊情況才能獲得解析解,通常只能用近似方法或數值方法求解。對于柱狀模型下的相變傳熱問題,1981年Lunardini借助熱平衡積分技巧,應用等效熱擴散率方法獲得了具有定常熱源邊界條件的柱型相變問題的一個近似解析解。2009年,Caldwell等應用焓法、邊界固定法、攝動法和熱平衡積分法分別求解了柱型相變傳熱問題,并就定常邊界條件的情況,對數值結果進行了分析和比較。
本文考慮在低溫邊界條件下,通過計算移動邊界每次向外推進固定距離時所需要的時間,構造了一種定空間步長方法數值求解向外柱型凝固問題,并對移動邊界的運動和固態介質內的溫度場進行了數值模擬,分析了低溫邊界條件對相變區域內的溫度變化及移動邊界運動的影響。
數學模型
考慮初始溫度恰好為相變溫度Tf的某液態介質由于邊界處溫度的變化所導致的向外柱型凝固問題(圖1),在相變過程中體積與物性均不發生變化的情況下,該問題的數學模型為

滿足的條件為

引進無量綱量
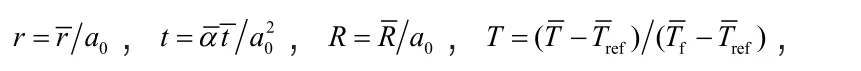
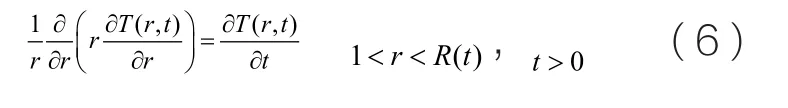

定空間步長方法
記Δr 為固定的空間網格步長,tj(t0=0)是對應于移動邊界位于Rj=1+jΔ r (j=0,1,…)處的時間。考慮相變界面移動到RN=1+NΔ r 處所對應的時間tN,此時各節點rj=1+jΔ r 處的固相介質的溫度記為由于控制方程可以簡化為
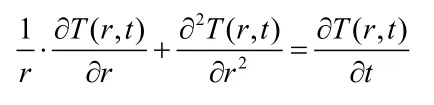
因此,應用向后差分格式離散時間導數項和中心差分格式離散空間導數項,則控制方程的離散形式為

Stefan條件(7)的離散形式為
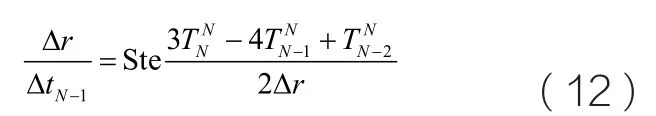
引入兩個變量a=1Δr 和b=ΔrΔtN-1,式(11)和(12)分別變為
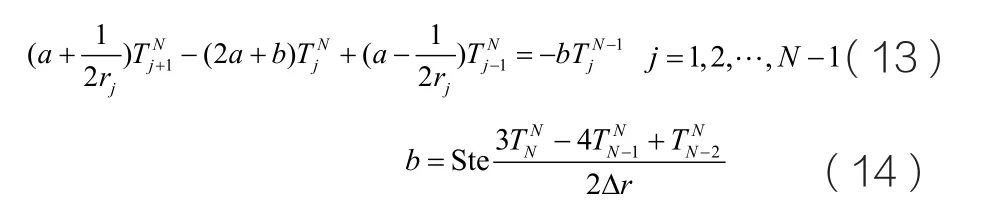
邊界條件(8)-(10)的離散形式分別為

數值結果與討論
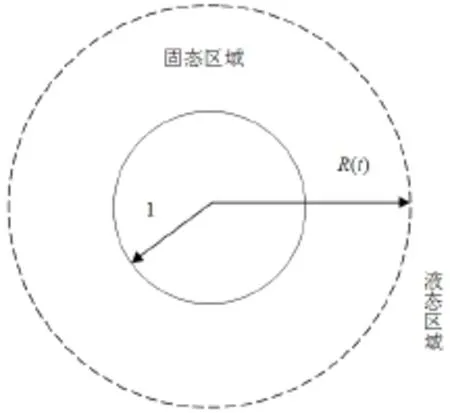
圖1 向外柱型凝固示意圖
在Stefan數Ste=0.2和f( t)=0的情況下,應用定空間步長方法,圖2(a)數值模擬了移動邊界位置隨時間變化的運動曲線和圖2(b)數值模擬了當移動邊界分別向外移動到R( t)=1.2,1.5和1.8時,相變區域內溫度的變化曲線,其中空間變量步長固定為Δr=0.001。表1對定空間步長方法所得到的不同時刻處移動邊界的位置與文獻中的相應結果進行了比較。從表中可以看出,在Stefan數Ste=0.2和邊界條件f( t)=0的情況下,定空間步長方法所得的結果與文獻中的焓法和攝動法所得到的相應結果非常接近,其絕對誤差均不超過0.001,從而表明了該數值方法求解柱型凝固問題的可行性和有效性。

圖2 在Ste=0.2和f( t)=0的情況下移動邊界的運動和相變區域內的溫度分布
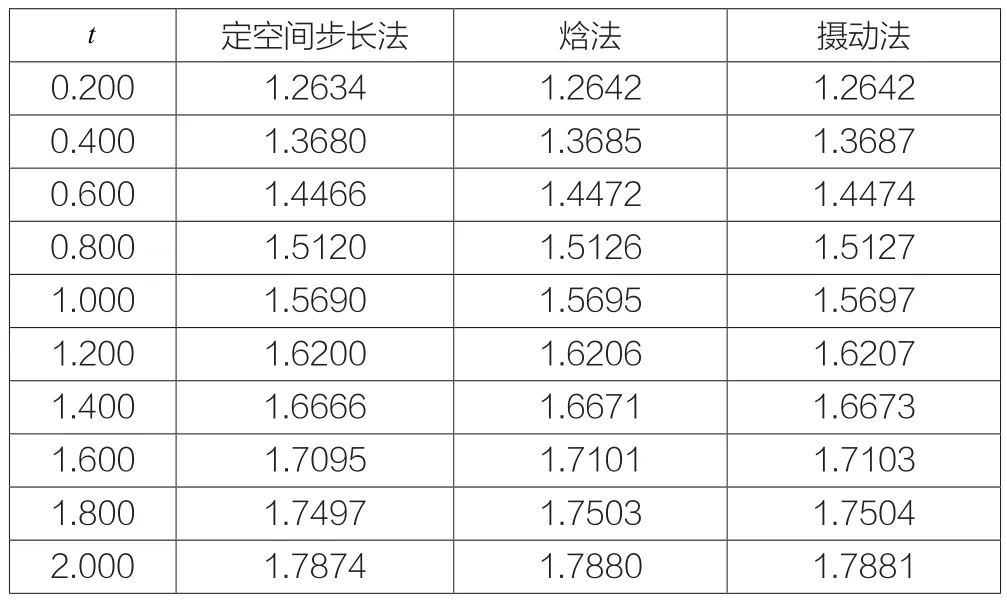
表1 在Ste=0.2和f( t)=0的情況下移動邊界位置的比較
在Stefan數Ste=0.2和f( t)=-t2的情況下,圖3(a)數值模擬了應用定空間步長方法所得到的移動邊界位置隨時間變化的運動曲線,圖3(b)數值模擬了當移動邊界分別向外移動到R( t )1.2,1.6和2.0時,所得到的相變區域內溫度的變化曲線,其中使用的空間變量步長為Δr=0.001。從圖3(a)中可以看出,在一段時間之后,移動邊界的位置隨時間的變化幾乎保持線性的運動趨勢,也就是說移動邊界的運動速度幾乎不變。從圖3(b)中可以看出,相變區域內的溫度場在快速變化,當移動邊界的位置從R( t)=1.6向外推進到R( t)=2.0時,相變區域內的溫差從大約1.8增加到了約4.3,這是受低溫邊界條件影響的結果。
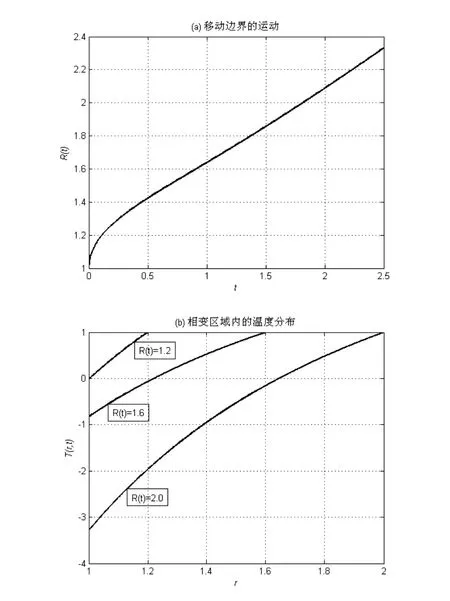
圖3 在Ste=0.2和f( t)=-t2的情況下移動邊界的運動和相變區域內的溫度分布
結束語
通過考慮相變界面每次向外推進固定距離時所需要的時間,構造了定空間步長方法用來求解向外柱型凝固問題,并模擬了相變過程中移動邊界的運動和固態介質內溫度場的變化。通過與已有結果比較可知,應用定空間步長方法求解向外凝固問題是可行的,并且具有較高的精度,從而表明了定空間步長方法在求解Stefan問題時所具有的重要應用價值。
DOI:10.3969/j.issn.1001-8972.2015.15.005

