風力機定量泵-并聯變量馬達主傳動系統并網控制

孔祥東　宋　豫　艾　超　王　靜

1.先進鍛壓成形技術與科學教育部重點實驗室(燕山大學),秦皇島,066004 2.燕山大學河北省重型機械流體動力傳輸與控制實驗室,秦皇島,066004

風力機定量泵-并聯變量馬達主傳動系統并網控制

孔祥東1,2宋豫1,2艾超1王靜1,2

1.先進鍛壓成形技術與科學教育部重點實驗室(燕山大學),秦皇島,066004 2.燕山大學河北省重型機械流體動力傳輸與控制實驗室,秦皇島,066004

提出了液壓型風力發電機組定量泵-雙并聯變量馬達主傳動系統并網的控制方法，即當首臺變量馬達處于并網狀態時采用恒壓控制方法實現下一臺變量馬達啟動時系統不失穩，并采用結構不變性原理對雙并聯變量馬達速度耦合進行解耦，當下一臺變量馬達啟動后采用轉速控制方法實現并網同步轉速控制;建立了系統并網控制的數學模型,并進行了仿真研究,得到了不同風速(定量泵轉速)條件下系統采用壓力與轉速控制的并網過程中定量泵轉速、變量馬達斜盤擺角、變量馬達轉速、系統高壓壓力的響應特性，驗證了定量泵-雙并聯變量馬達系統并網控制方法的有效性,為拓展液壓型風力發電機組在大型及超大型機型中的應用奠定了理論基礎。

風力發電;定量泵-并聯變量馬達;并網控制;壓力控制;轉速控制

0　引言

隨著傳統能源儲量的急劇減少，人們對新能源的關注與研究正在不斷地深入。風能作為潔凈的可再生能源的一種，已經受到很多國家的重視，風電產業正在飛速發展。風中蘊含著用之不盡的能源，但是，目前風電行業面臨著一個重要的問題是并網困難，主要是由于風力發電機組的電能質量不能滿足電網要求，這就導致裝機容量與發電量之間存在巨大的差距，設備不能發揮其能力。傳統的風力發電機組機型主要是雙饋型和直驅型，雙饋型通過齒輪箱給主軸升速從而帶動交流異步電動機,直驅機型風輪主軸直接與永磁同步發電機相連，兩種機型最大的問題是傳動系統無法消除風速波動對電能質量的影響。新型的液壓型風力發電機組應用了液壓系統無級調速與功率密度高的優勢，有效降低功率波動的同時還減小了機組的重量，降低了裝機成本，是未來風電發展的一種主要機型。2009年，蘇格蘭Artemis Intelligent Power公司采用數字定量泵-并聯數字變量馬達傳動形式，進行了1.5MW液壓型風力發電機組模型研究[1]。2010年，德國亞琛工業大學采用徑向柱塞泵和軸向柱塞馬達系統，搭建定量泵-并聯變量馬達實驗系統,對其運行特性進行了實驗研究[2-3]。但以上研究均未見應用的相關報道，沒有實現產業化。

采用定量泵-并聯變量馬達系統作為風力發電機組動力傳輸機構，能夠有效地提升機組的性能。研究者針對定量泵-并聯變量馬達系統進行了廣泛的研究。文獻[4]在定量泵-并聯變量馬達系統中采用壓力規劃法降低系統壓力波動,同時在轉速控制中加入擾動觀測器，提高了系統的抗干擾能力和穩態精度；文獻[5]對單泵多并聯馬達系統進行分層協調控制，根據一階滑模觀測器估算的道路條件確定最優滑移率，實現車輛優越的加速和減速性能；文獻[6]針對越野性能要求高的步兵戰車驅動系統,結合恒壓網絡技術提出改進的MRAC(Narendra model reference adaptive control)方法實現雙馬達速度同步控制,降低了壓力波動，對負載干擾具有較強的魯棒性;文獻[7]分析了單變量泵并聯變量馬達的同步轉速控制,利用基于流量均衡控制與壓力速度之和反饋相結合的控制策略，無需解耦即可實現工程車輛同步控制。

本文以液壓型風力發電機組主傳動系統作為研究對象，采用定量泵-雙并聯變量馬達系統實現并網控制。提出了基于系統恒壓控制[8-10]的雙并聯變量馬達轉速控制[11-13]方法,有效解決了雙并聯變量馬達啟動時對系統的壓力沖擊問題，使同步發電機滿足并網要求。

1　液壓型風力發電機組工作原理

液壓型風力發電機組定量泵-雙并聯變量馬達主傳動系統原理如圖1所示,主要由風力機、定量泵-雙并聯變量馬達液壓系統、同步發電機組成。

圖1　液壓型風力發電機組主傳動系統原理圖

風力機吸收風能并傳遞至定量泵,定量泵輸出高壓油帶動變量馬達旋轉,變量馬達帶動同步發電機將液壓能轉化為電能送入電網。

為了提高系統的效率與風能利用率，在風速低于雙發電機并網閾值時，系統只投入一臺變量馬達及與其相連的發電機，當風速高于這一閾值時，開關閥打開，系統投入第二臺變量馬達及與其相連的發電機，實現雙并聯發電機發電。

2　定量泵-雙并聯變量馬達系統數學模型

液壓型風力發電機組定量泵-雙并聯變量馬達主傳動系統回路原理簡圖見圖2。

采用圖2所示的原理圖模型推導定量泵-雙并聯變量馬達系統傳遞函數時，兩臺變量馬達型號相同，故其數學表達相同，以下角標1和2區別,并作如下假設：①連接管道為硬管且長度很短;②液壓泵和馬達腔的容積為常數;③系統中高低壓腔的壓力分別均勻相等；④不考慮補油系統。

圖2　定量泵-雙并聯變量馬達主傳動系統回路原理簡圖

在工作點處將斜盤擺角γ與高壓管路壓力ph的乘積構成一個非線性方程進行線性化處理，有

γph=(γ(0)+Δγ(t))(ph(0)+Δph(t))

(1)

式中，γ為變量馬達斜盤擺角,為[0,1]區間取值的量綱一數值；γ(0)為變量馬達初始斜盤擺角,rad；Δγ(t)為變量馬達初始斜盤擺角變化量，rad；ph(0)為高壓管路初始壓力,Pa;Δph(t)為高壓管路壓力變化量,Pa。

忽略二階無窮小量，整理得

γph=γ0ph0+Δγ(t)ph0+γ0Δph(t)

(2)

式中,ph0為高壓管路初始壓力，Pa；γ0為變量馬達初始斜盤擺角，rad。

變量馬達與負載的力矩平衡方程的拉氏變換式為

Kmγph0+Kmγ0ph=Jms2θm+Bmsθm+Gmθm+Tm

(3)

式中,Km為變量馬達排量梯度，m3/rad；θm為變量馬達轉角，rad；Jm為變量馬達與負載(折算到變量馬達軸上)的總慣量，kg·m2；Bm為變量馬達軸端的黏性阻尼系數，N·s/m；Gm為變量馬達軸端的負載彈簧剛度，N/m；Tm為作用在變量馬達上的電磁轉矩，N·m。

定量泵-雙并聯變量馬達高壓腔流量連續性方程為

(4)

式中，qp為定量泵流量，m3/s；qm為變量馬達流量，m3/s；V0為定量泵與變量馬達之間高壓管路總容積，m3；βe為油液綜合體積彈性模量,Pa。

將變量馬達流量方程代入式(4)有

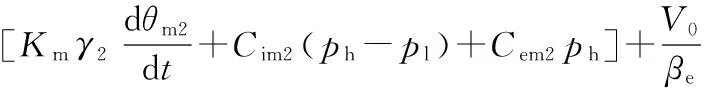
(5)

式中,pl為低壓管路壓力，Pa；Cim、Cem分別為變量馬達內外泄漏系數,m3/(s·Pa)。

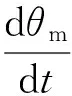
(6)

式中,ωm0為變量馬達轉速初始值,rad/s;Δωm(t)為變量馬達轉速變化值,rad/s。

將式(6)代入式(5),則其拉氏變換式為

qp=(Kmγ1ωm01+Kmγ01sθm1)+

(7)

式中,Ctm為變量馬達總泄漏系數,Ctm=Cim+Cem。

由變量馬達流量方程與式(4)、式(7)得到定量泵-雙并聯變量馬達系統傳遞函數為

qm1=Dm1ωm1+Cim1(ph-pl)+Cem1ph

(8)

qm2=Dm2ωm2+Cim2(ph-pl)+Cem2ph

(9)

Kmγ1ph0+Kmγ01ph=Jm1s2θm1+Bm1sθm1+Gm1θm1+Tm1

(10)

Kmγ2ph0+Kmγ02ph=Jm2s2θm2+Bm2sθm2+Gm2θm2+Tm2

(11)

qp=Kmγ1ωm01+Kmγ01sθm1+Kmγ2ωm02+

(12)

由定量泵流量方程和式(8)～式(12),聯立可得定量泵-雙并聯變量馬達系統傳遞函數方框圖，見圖3。

圖3　定量泵-雙并聯變量馬達系統方框圖

當定量泵和兩變量馬達輸出端剛度很大時,Gm1=Gm2=Gp=0。圖3中共包含5個輸入量γ1、γ2、Tp、Tm1、Tm2和3個輸出量θp、θm1、θm2,系統高壓壓力ph為中間變量。

由式(11)得

ph=

(13)

式中,ωp為定量泵轉速，rad/s；Dp為定量泵排量，m3/rad；Ct為總泄漏系數,即定量泵總泄漏系數與變量馬達總泄漏系數之和，m3/(s·Pa)。

將式(13)代入定量泵力矩平衡方程得

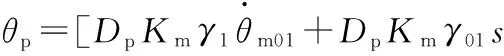
(14)

式中，θp為定量泵轉角，rad；Tp為作用在定量泵上的驅動力矩，N·m；Jp為定量泵和負載(折算到定量泵軸上)的總慣量，kg·m2；Bp為定量泵軸端的黏性阻尼系數,N·s/m；Gp為定量泵軸端的負載彈簧剛度，N/m。

3　定量泵-雙并聯變量馬達系統并網控制策略

3.1并網控制器設計思想

當變量馬達1工作于并網狀態、變量馬達2未啟動時，根據管道中流量平衡的原理，檢測定量泵轉速可以給定變量馬達斜盤擺角，即在恒流狀態下給定變量馬達1斜盤擺角基準值。

當變量馬達1工作于并網狀態、變量馬達2啟動時，檢測風速信號和定量泵轉速信號，送入壓力給定控制器，其輸出與系統實際壓力信號的差值送入壓力控制器,控制變量馬達1斜盤擺角進行調整，實現系統高壓壓力基本穩定在給定值，即在恒壓狀態下進行變量馬達2啟動。定量泵轉速受變量馬達1斜盤擺角與變量馬達2斜盤擺角的共同作用，當定量泵輸入轉速為定值時，可采用結構不變性解耦原理，實現系統轉速控制環節互不相關，即變量馬達2斜盤擺角和轉速變化均不會影響系統高壓壓力，系統壓力只由變量馬達1斜盤擺角決定，通過變量馬達1擺角控制器控制，實現系統高壓壓力恒定。

當變量馬達1工作于并網狀態、變量馬達2啟動、系統工作于恒壓狀態時，系統穩定于(1500±6)r/min的并網同步轉速下，實現變量馬達2進入并網工作狀態。

3.2并網控制器設計

根據圖4所示的并網流程,可實現定量泵-雙并聯變量馬達系統并網控制器的設計,但是,由式(13)分析可知，無論變量馬達1斜盤擺角、變量馬達2斜盤擺角、變量馬達2外負載中哪一參量改變,都會引起系統高壓壓力變化，即兩轉速控制通道相互耦合。

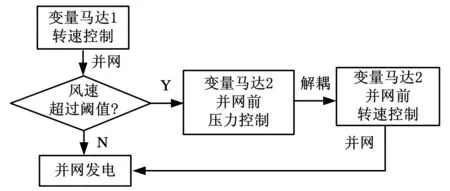
圖4　定量泵-雙并聯變量馬達系統并網流程圖

變量馬達在調整轉速過程中,由于風力機轉動慣量很大對其轉速的影響不大，故可以認為定量泵轉速不變；變量馬達1處于并網狀態時，其轉速被電網拖住為定值，化簡定量泵-雙并聯變量馬達系統傳遞函數，其簡化方框圖見圖5。

圖5　定量泵-雙并聯變量馬達系統簡化方框圖

分析圖5可知,若要保證高壓壓力不變,則需令A點流量不變,而A點流量變化受變量馬達1和變量馬達2兩部分變化影響：

(15)

(16)

式中,Δqm1、Δqm2分別為變量馬達1、2引起的A點流量變化，m3/s。

由A點流量不變的要求得

ΔqA=Δqm1+Δqm2=0

(17)

式中,ΔqA為A點流量變化，m3/s。

由式(15)～式(17)聯立得

(18)

由式(18)可以看出，通過實時檢測變量馬達2斜盤擺角和變量馬達2轉速的變化值，即可計算出變量馬達1斜盤擺角的補償值送入控制器，在此利用結構不變性解耦補償方法實現了系統恒壓控制。

基于以上分析可以得出定量泵-雙并聯變量馬達控制系統簡圖見圖6,系統共包括5個控制器:壓力給定控制器、壓力控制器、變量馬達1斜盤擺角控制器、變量馬達2斜盤擺角控制器、斜盤擺角補償控制器。

通過上述理論分析，該方法可擴展到定量泵-多并聯變量馬達系統,實現多臺發電機依次并網,從而拓展液壓型風力發電機組在大型及超大型機型中的應用。

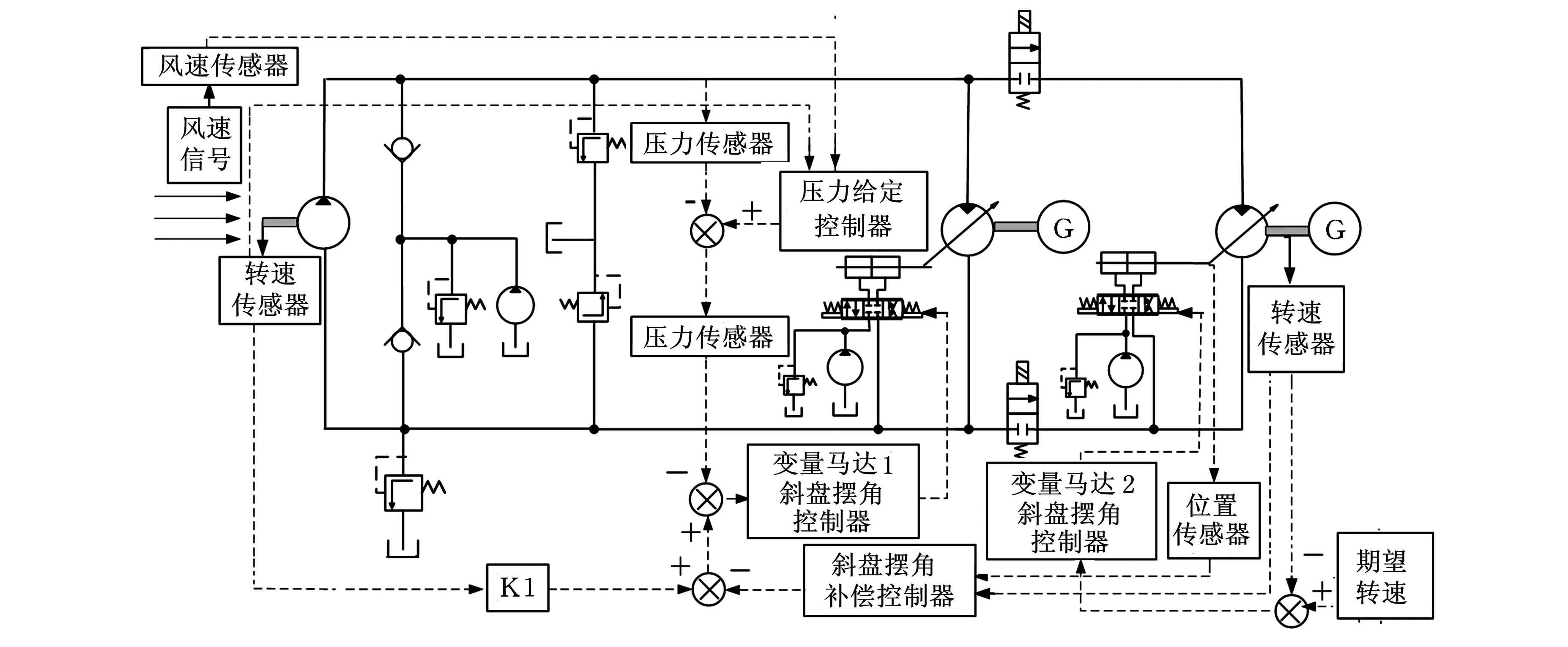
圖6　定量泵-雙并聯變量馬達控制系統簡圖

4　定量泵-雙并聯變量馬達系統并網控制仿真研究

4.1仿真平臺

利用AMESim與MATLAB/Simulink軟件搭建了液壓型風力發電機組定量泵-雙并聯變量馬達主傳動液壓控制系統仿真模型，如圖7所示，采用該模型對不同風速變化條件下高壓壓力、變量馬達斜盤擺角、變量馬達轉速響應特性進行了分析。

圖7　液壓控制系統仿真模型

針對液壓型風力發電機組設置主傳動液壓系統仿真參數如表1所示。

表1　主傳動液壓系統仿真參數表

風力機大部分時間工作在局部負荷區，通過實時檢測風速，并從風力機氣動轉矩特性獲取風功率值，便可計算出系統高壓壓力給定值。

對于液壓型風力發電機組，風速取值范圍為4～13 m/s。當并聯變量馬達處于并網狀態且風速不變時，計算得出系統高壓壓力給定值如表2所示。

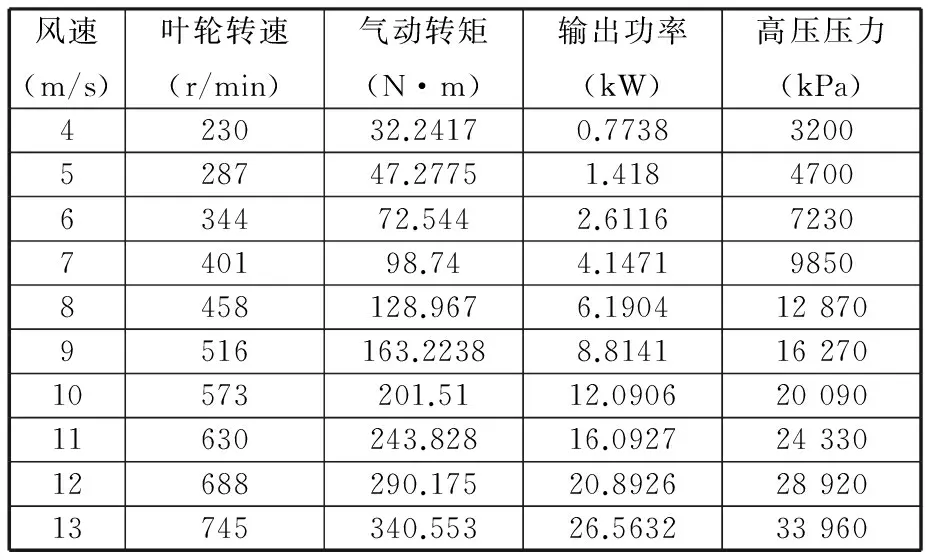
表2　高壓壓力參數設定

4.2仿真結果分析

圖8所示為風速9 m/s時變量馬達2進入并網狀態前系統響應仿真結果。在第10s將變量馬達2啟動。

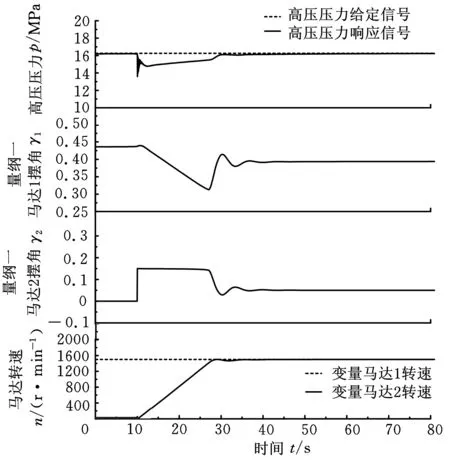
圖8　風速9m/s時系統仿真結果

分析圖8的結果可知，當風速(定量泵轉速)不變，系統穩定于某一狀態時，變量馬達2進入并網狀態前，變量馬達1保持穩定的并網轉速，變量馬達2轉速按要求提升至并網轉速，并控制高壓壓力快速穩定于恒值，確保系統不失穩。

圖9、圖10所示為風速6～9 m/s斜坡變化、(8+0.5sint)m/s正弦變化時變量馬達2進入并網狀態前系統響應仿真結果。在第10s將變量馬達2啟動。

圖9　風速6～9 m/s斜坡變化時仿真結果

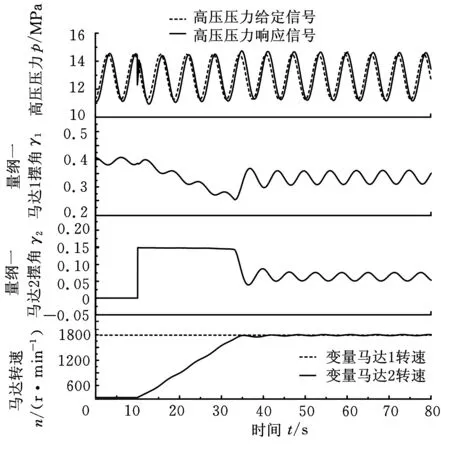
圖10　風速(8+0.5sint)m/s正弦變化時仿真結果

分析圖9、圖10的結果可知,當風速(定量泵轉速)分別為斜坡變化、正弦變化時,解耦控制方法均可實現變量馬達1在并網條件下、變量馬達2進入并網狀態前,對系統高壓壓力的穩定控制,保證變量馬達2啟動直至達到并網狀態，系統高壓壓力在一定范圍內波動，滿足系統控制要求。

由圖8～圖10結果可以看出,當風速(定量泵轉速)按照上述情況變化時,變量馬達1能夠在變量馬達2啟動時迅速調整斜盤擺角，滿足并網的同步轉速要求，并且兩臺變量馬達能夠快速跟蹤風速變化使系統的高壓壓力在變化過程中均只有小幅波動并很快恢復穩定狀態，保證并網對系統壓力的控制要求。同時，變量馬達2的轉速逐漸升高并穩定到并網同步轉速，此過程實質上就是定量泵流量的分流過程。仿真結果從理論上驗證了定量泵-雙并聯變量馬達系統并網控制方法的有效性。

5　結論

(1)對液壓型風力發電機組定量泵-雙并聯變量馬達系統的數學模型進行了分析,得到了第二臺變量馬達并網時，解決系統高壓壓力穩定控制的解耦控制方法,抑制了兩臺變量馬達斜盤擺角變化時因互相耦合導致的系統高壓壓力波動。

(2)采用并網前系統恒壓狀態下并聯馬達恒轉速控制策略，實現了并聯兩臺變量馬達的并網控制，可防止液壓系統失穩，獲得良好的控制效果，從而保證了雙并聯變量馬達順利達到并網要求。

[1]Tsutsumi K,Shimizu M,Maekawa A,et al.Power Generating Apparatus of Renewable Energy Type:US,20130067900[P].2011-12-1.

[2]Kohm?scher T.Modell Bildung Analyse und Auslegung Hydrostatischer Antriebsstrangkonzepte[D].Aachen,Germany:RWTH Achen,2008.

[3]Johannes S,Nils V,Hubertus M.Hydrostatic Drive Train in Wind Energy Plants[C]//EWEA 2011 Brussels Europe’s Premier Wind Energy Event Scientific,Proceedings European Wind Energy Conference & Exhibition.Brussels,2011:20-23.

[4]鄭琦,李運華,楊麗曼.控并聯變量馬達速度系統復合控制策略[J],北京航空航天大學學報,2012,38(5):692-696.

Zheng Qi,Li Yunhua,Yang Liman.Compound Control Strategy for the Pump-controlled-parallel-variable-displacement-motor Speed System[J].Journal of Beijing University of Aeronautics and Astronautics,2012,38(5):692-696.

[5]Li Yunhua,He Liuyu,Yang Liman.Coordinated and Optimal Acceleration and Deceleration Driving Control for Multi-axle Hydrostatic Driving Vehicle [C]//12th International Conference on Control,Automation,Robotics and Vision.Guangzhou,2012:524-529.

[6]Wu Baolin, Qiu Lihua, Wang Zhanlin.Four Wheels Driven Independently by One Pump Drlving Four Hydraullc Motors[J].Chinese Journal of Mechanical Engineering,2005,18(2):232-236.

[7]吳保林,裘麗華,唐志勇,等.工程機械液壓底盤模擬實驗臺雙馬達同步技術研究[J].中國機械工程,2006,17(9):899-902.

Wu Baolin,Qiu Lihua,Tang Zhiyong,et al.Research on Speed Synchronization Control of Double Motors of Hydraulic Chassis Simulation Experimental Device of Engineering Vehicles[J]. China Mechanical Engineering,2006,17(9):899-902.[8]Schachles C,Schachles P,Schachles E,et al.Wind Power Generating System:US,4503673[P].1979-05-25.[9]David M,Tracy C.Hydraulic Control Device for Wind Turbine:US,4715782[P].1998-10-29.

[10]查普驅動公司.渦輪機速度穩定控制系統:中國,200980136335.3[P].2010-03-25.

[11]Ding Haigang,Zhao Jiyun.Characteristic Analysis of Pump Controlled Motor Speed Servo in the Hydraulic Hoister[J].International Journal of Modelling, Identification and Control,2013,19(1):64-74.[12]Triet Hung Ho,Kyoung Kwan Ahn.Design and Control of a Closed-loop Hydraulic Energy-regenerative System[J].Automation in Construction,2012,22:444-458.

[13]白國長,祁曉野,王占林.具有相乘非線性的馬達速度魯棒控制[J],北京航空航天大學學報,2008,34(7):803-806.

Bai Guochang,Qi Xiaoye,Wang Zhanlin.Motor Speed Robust Control with Multiplying Nonlinear Property[J].Journal of Beijing University of Aeronautics and Astronautics,2008,34(7):803-806.

(編輯蘇衛國)

Grid Connected Control in Fixed Displacement Pump-Parallel Variable Motor of Main Transmission System in Wind Turbine

Kong Xiangdong1,2Song Yu1,2Ai Chao1,2Wang Jing1,2

1.Key Laboratory of Advanced Forging & Stamping Technology and Science(Yanshan University), Ministry of Education of China,Qinhuangdao,Hebei,066004 2.Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control,Yanshan University,Qinhuangdao,Hebei,066004

A grid connected control method was presented herein,which was used in the main transmission system of the fixed displacement pump-double parallel variable motor in hydraulic wind turbine,namely when the first variable motor worked in the state of grid connected,another variable motor didn’t lose stability in startup under the constant pressure control method.The rotate speed coupling of the double parallel variable motor was eliminated with the principle of structure invariance,therefore,when another variable motor was post-launch,the grid connected synchronous rotate speed was controlled under the speed control method.Meanwhile,the grid connected control mathematical model was established,and simulation was conducted.With pressure and speed control,the fixed displacement pump rotate speed,the variable motor swashplate angle,the variable motor rotate speed and the system high pressure response characteristics in the process of grid connected were obtained under the condition of different wind speed (fixed-displacement pump rotate speed).The grid connected control method was verified in the fixed displacement pump-double parallel variable motor.This reserach lays a theoretical foundation to expand the hydraulic wind turbine in the applications of large and super large wind turbine.

wind power generation;fixed displacement pump-parallel variable motor; grid connected control; pressure control; speed control

2015-03-15

國家自然科學基金資助項目(51475406;51405423;51375422)

TH137DOI：10.3969/j.issn.1004-132X.2015.16.015

孔祥東,男,1959年生。燕山大學機械工程學院教授、博士研究生導師。主要研究方向為流體傳動及控制、液壓型風力發電機組等。發表論文180余篇。宋豫,男,1986年生。燕山大學機械工程學院博士研究生。艾超,男,1982年生。燕山大學機械工程學院講師、碩士研究生導師。王靜,女,1987年生。燕山大學機械工程學院碩士研究生。