隱式功能函數結構體可靠性拓撲優化

吳勁松　周金宇

江蘇理工學院常州市裝備再制造工程重點實驗室,常州,213001

隱式功能函數結構體可靠性拓撲優化

吳勁松周金宇

江蘇理工學院常州市裝備再制造工程重點實驗室,常州,213001

考慮工程實際中外載荷、材料屬性等的隨機不確定性對結構安全性的影響，研究了具有結構位移可靠性約束的拓撲優化設計。建立以柔度最小為目標、以單元相對密度為變量、具有材料體積分數約束和結構位移可靠性約束的拓撲優化數學模型；針對運用有限元數值計算方法時結構功能函數為隱式的情況，運用響應面法近似逼近結構真實的功能函數；利用簡便高效的一次二階矩法計算結構位移可靠度;采用內循環為確定性的拓撲優化、外循環控制結構材料體積分數的策略對連續體結構進行可靠性拓撲優化設計。通過兩個算例與確定性拓撲優化結果進行比較,結果表明所提設計方法是高效可行的。

可靠性;拓撲優化;隱式功能函數;響應面法

0　引言

連續體結構拓撲優化一直是結構設計中的難點和熱點問題。目前對連續體結構拓撲優化的研究已經有了長足的發展，形成了均勻化方法[1]、變密度法[2]、漸進結構優化法、雙向漸進結構優化方法[3-4]以及水平集法[5]等拓撲優化方法。當前對拓撲優化的研究大多是基于確定性假設，沒有考慮實際工程中載荷、材料屬性、結構尺寸等的不確定性。由于沒有考慮這些不確定性因素對結構的影響，所以確定性的拓撲優化得到的結構安全裕度較低，對于一些對隨機變量敏感的問題，確定性拓撲優化很難保證結構的可靠性和安全性。

在拓撲優化過程中將載荷、材料屬性等參數視為隨機變量，將結構的可靠性作為拓撲優化問題的約束條件之一，研究結構的可靠性拓撲優化，在求解算法中將結構可靠性理論和拓撲優化技術進行有機融合，由于定量計入了影響結構性能的各種不確定因素，因此結構可靠性拓撲優化設計能在安全性和經濟性之間達到最佳平衡，從而有效克服了傳統結構優化設計的不足，使設計結果更趨合理[6]。近年來可靠性拓撲優化的研究引起了許多學者的重視,文獻[7-8]運用一種啟發式策略先對隨機變量進行修正使其滿足結構的可靠性要求，再用修正后的隨機變量進行確定性的拓撲優化研究；文獻[9-10]分別利用漸進結構優化法和雙向漸進結構優化法結合響應面法對具有可靠性約束的拓撲優化進行了討論；文獻[11-12]通過隨機有限元法將結構的拓撲優化視為一種對單元的模式識別，研究了隨機變量服從正態分布和非正態分布的連續體可靠性拓撲優化問題。迄今為止,對連續體可靠性拓撲優化研究大都是將可靠性分析和拓撲優化同時進行，每步拓撲優化迭代都要計算一次結構的可靠性，存在計算量大、計算效率低和精度難以保證等問題。同時，在可靠性分析過程中,對于結構功能函數為隱式時如何計算結構可靠性也沒有做詳細的闡述。

本文在傳統的拓撲優化設計研究的基礎上，基于變密度法建立了具有結構位移可靠性約束的拓撲優化模型，利用響應面法對隱式的結構功能函數近似逼近，再進一步算得結構的位移可靠性指標。將可靠性分析和拓撲優化設計分開進行研究，通過內循環是確定性拓撲優化、外循環是控制材料體積分數大小這種內外循環策略實現對結構的可靠性拓撲優化研究。最后通過兩個算例來驗證文中方法的可行性。

1　可靠性拓撲優化基本模型

拓撲優化就是在給定的設計區域內尋求滿足約束條件下的最優結構傳力路徑和材料分布。經典的拓撲優化設計是在給定的材料體積分數下尋求具有柔度最小的最優拓撲結構，其基于變密度法的數學模型為[13]

(1)

式中,xi為材料單元的相對密度,即設計變量;ui為材料單元位移列向量;k0為材料密度為“1”的單元剛度矩陣;xmin為最小材料單元密度,通常取為0.01;vi為材料單元相對體積;p為懲罰因子;C為結構整體的柔度值;K為整體結構剛度矩陣;U為整體位移列向量;F為外載荷向量;V為整體結構體積;V*為優化后的結構體積;f為給定的材料體積分數。

由式(1)可以看出：經典的拓撲優化尋求的是在給定材料體積分數下具有柔度最小即剛度最大的最優結構。在結構設計中我們更多時候關心的是結構在外載荷作用下最大位移是否滿足設計要求。經典的確定性拓撲優化得到的優化結構僅僅是滿足剛度最大，至于結構最大位移、最大應力等是否滿足設計要求都無法得知。此外，實際工程中的載荷、材料性能、結構尺寸等都是不確定的。因此，單純研究確定性拓撲優化所得到的結構顯然會存在很多缺陷，更加沒有可靠性保障。現考慮與結構剛度密切相關的結構位移可靠性，建立基于變密度法具有位移可靠性約束的拓撲優化數學模型如下：

(2)

式中,P[g(X)=δ*-δi≥0]>P*為結構的可靠性約束;P*為結構允許可靠度;δi為單元的位移;δ*為結構許用的最大位移。

2　隱式功能函數的近似逼近

連續體可靠性拓撲優化設計的可靠性約束為

P[g(X)=δ*-δi≥0]>P*

(3)

其中g(X)=δ*-δi≥0為結構安全狀態下的功能函數。對式(3)的求解需要計算每個單元的可靠性。如果結構位移最大的單元都能滿足

P[g(X)=δ*-max{δ(i)|i=1,2,…,n}≥0]>P*

(4)

那么整個結構就一定能滿足可靠性要求,所以問題就可以簡化成只需計算位移最大的單元的可靠性約束。假設隨機變量都服從正態分布，結構處在安全域內的功能函數為

g(X)=δ*-max{δ(i)|i=1,2,…,n}>0

(5)

g(X)>0的概率為

P[g(X)>0]=1-P[g(X)≤0]=

(6)

式中,Φ(·)表示標準正態變量的累積分布函數;ug和σg分別表示結構功能函數的均值和標準差。

式(6)表明,結構可靠度和可靠性指標之間是一一對應的關系。根據結構可靠性指標的定義,β可表示為在標準化正態空間S中從坐標原點到失效面的最短距離,即

(7)

其中，si是將隨機變量標準化后的標準正態變量。隨機變量標準化方程為

(8)

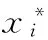
由以上分析可以看出,只要知道結構的功能函數,利用簡單的一次二階矩法就可以很方便地得到結構的可靠度,但此處結構功能函數式(5)是一個隱式,無法得知它的準確表達式，這就給一次二階矩法的應用帶來了巨大困難。針對這種情況,可采用響應面法求解。

響應面法通過合理選取試驗點和迭代策略來保證多項式函數能夠在失效概率上收斂于真實的隱式極限狀態函數的失效概率。用于擬合的多項式有很多種，其中二次不含交叉項的響應面由于結構簡單、運算量小、精度相對較高被廣泛應用。二次不含交叉項的響應面的功能函數為

(9)

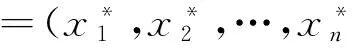
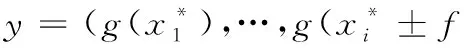
(10)

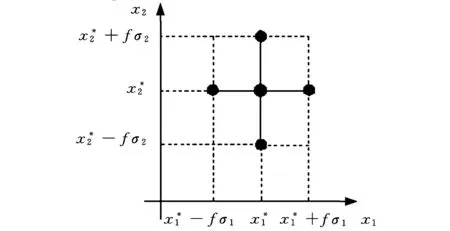
圖1　試驗點選取示意圖

利用最小二乘法求得線性響應面的待定系數

b=(ATA)-1ATy

(11)

其中，A是由2n+1個試驗點xl1,xl2,…,xln(l=1,2,…2n+1)組成的(2n+1)×(2n+1)階樣本矩陣:

A=

(12)

(13)

經過一次迭代可得近似功能函數,如圖2a所示;經過多次迭代則不斷接近真實功能函數，如圖2b所示,直到相鄰兩次迭代算得的可靠性指標滿足|βj-βj-1|<0.001,則停止迭代,輸出結果β。

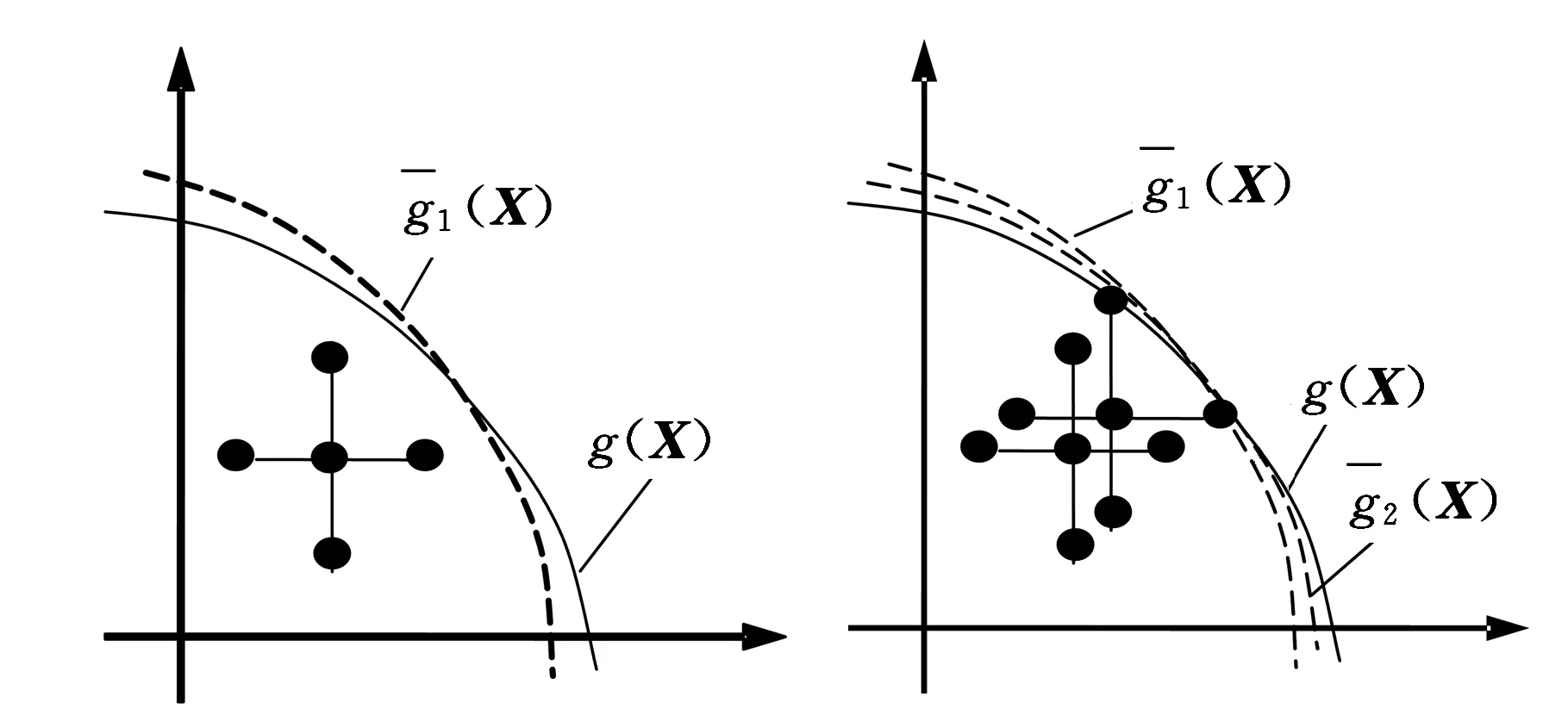
(a)一次迭代(b)多次迭代圖2　響應面法獲取近似功能函數

3　高效可靠性拓撲優化流程

可靠性拓撲優化研究的難點是如何將可靠性分析和拓撲優化簡單高效地結合在一起，克服計算量大的困難并且保證所需精度。在當前的求解方法中,可靠性分析和結構拓撲優化是在同一迭代循環內完成的，即首先通過相應優化準則對結構進行優化，每次迭代后再利用有限元分析得到結構的位移和應力，然后進行可靠性分析，最后判斷是否滿足可靠性約束和其他約束要求。如果不滿足, 再重新優化直到滿足設計約束[14-16]。但每次迭代結構的拓撲形狀都發生變化，需要重新計算結構可靠性。同時，由于變化的無規律性，導致無法得知結構功能函數的表達式，給可靠性計算帶來困難。所以將可靠性分析放在拓撲優化過程中，存在重復計算可靠性的問題，增加了求解計算量。

拓撲優化實質就是通過一定的方法逐漸去除對結構性能貢獻小的材料,保留對結構性能貢獻大的材料。材料去除得越多,對應確定性拓撲優化即式(1)中的體積分數f越小,經過拓撲優化得到的結構只是滿足剛度最大，是否能滿足位移可靠性的約束則需要進一步驗證。可以明確的是,f越大,結構受載后的最大位移肯定越小，對應的位移可靠性也越高。去除的材料過多，結構的可靠性就無法得到保障；去除的材料過少，結構又過于保守,達不到優化的目的[17]。

因此,通過控制材料體積分數，找到合適的體積分數f能使結構安全性和經濟性達到最佳平衡，就能解決可靠性拓撲優化問題。綜上所述，可以利用內外循環的策略，內循環為確定性拓撲優化,外循環為控制材料體積分數f的大小。首先給定一個初始體積分數f，進行確定性拓撲優化即內循環，然后對優化后的結構進行有限元分析，并結合響應面法得到結構的功能函數，最后利用式(7)算出可靠性指標β。如果可靠性指標小于給定的指標β<β*,則說明去除材料過多,這時增大體積分數f，返回確定性拓撲優化前的模型，再次運行內循環，直到β≥β*,再進一步判斷是否滿足可靠性指標收斂準則:

|β-β*|≤ξ

(14)

如果不滿足則說明結構還有優化空間,這時再減小體積分數f運行內循環。通過二分法增大或者減小材料體積分數直到滿足式(14)為止，整個優化流程如圖3所示。

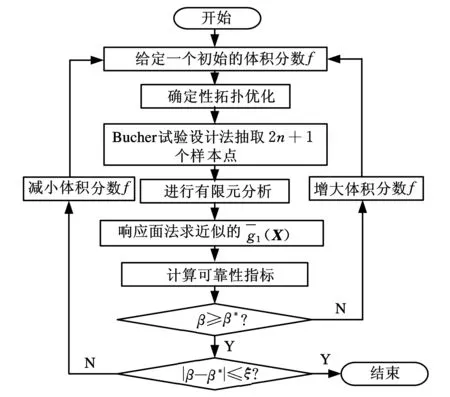
圖3　可靠性拓撲優化流程框圖

4　算例

4.1算例一

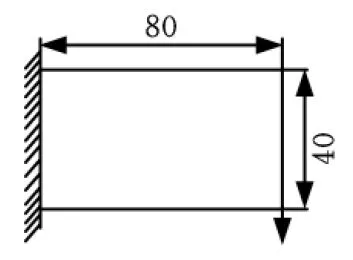
圖4　懸臂梁的設計域

圖5　不考慮可靠性的優化結果

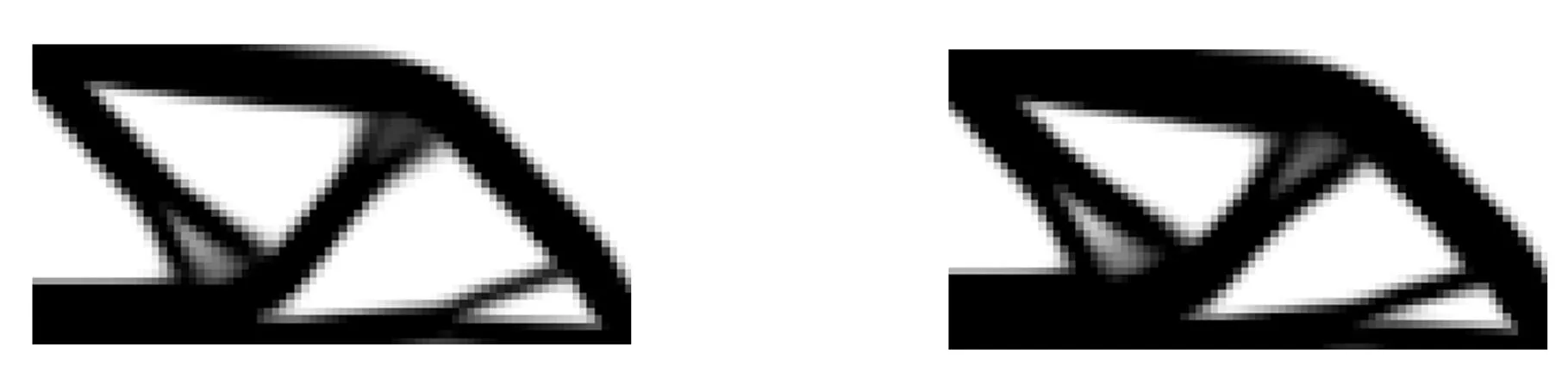
(a)β=4.0(b)β=2.0圖6　考慮位移可靠性約束的優化結果

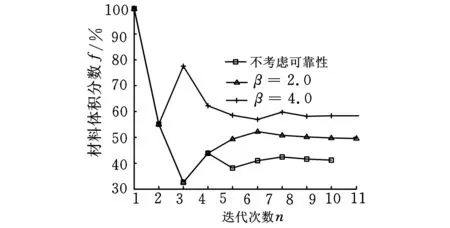
圖7　算例一迭代歷程

4.2算例二

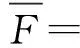
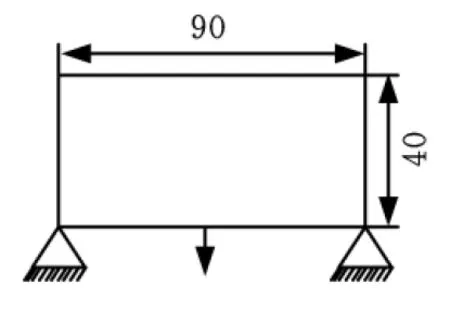
圖8　初始的設計域

圖9　不考慮可靠性的優化結果

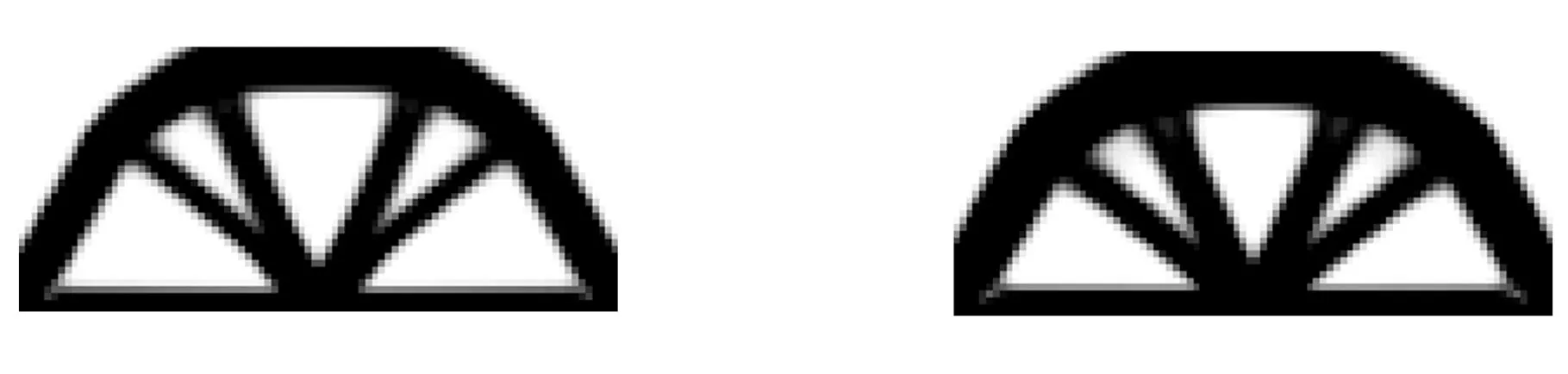
(a)β=4.0(b)β=2.0圖10　考慮位移可靠性約束的優化結果

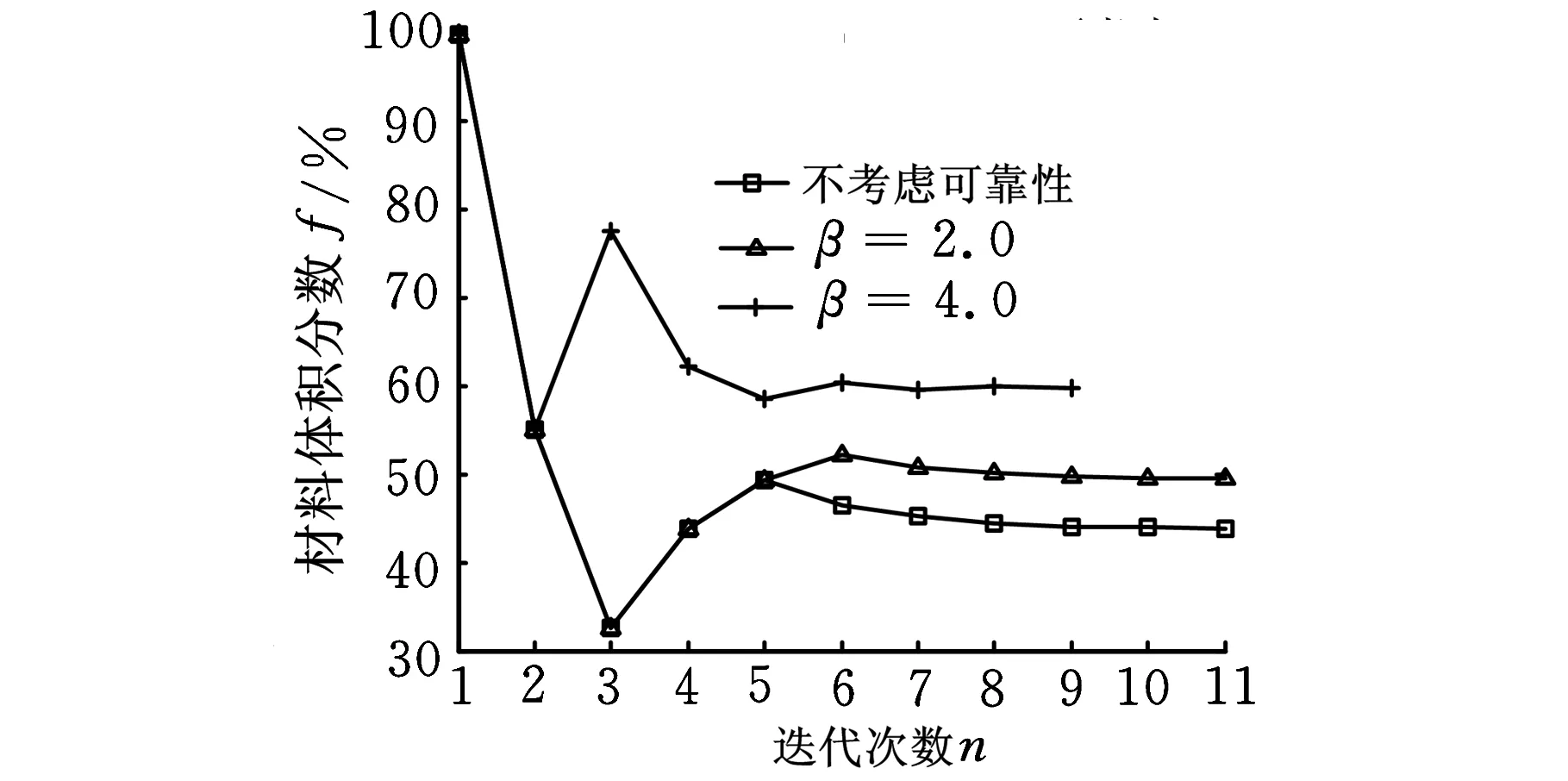
圖11　算例二迭代歷程

表1所示為算例一、算例二分別考慮可靠性和不考慮可靠性的優化結果數據，可以看出，考慮可靠性約束優化結構的最大位移明顯小于不考慮可靠性約束結構的最大位移，因此考慮可靠性所得結構更加合理。同時，由于定量考慮了結構的可靠性，所以結構不僅能滿足剛度最大而且有一定的可靠性保證，從而實現了結構經濟性和安全性的最佳平衡。

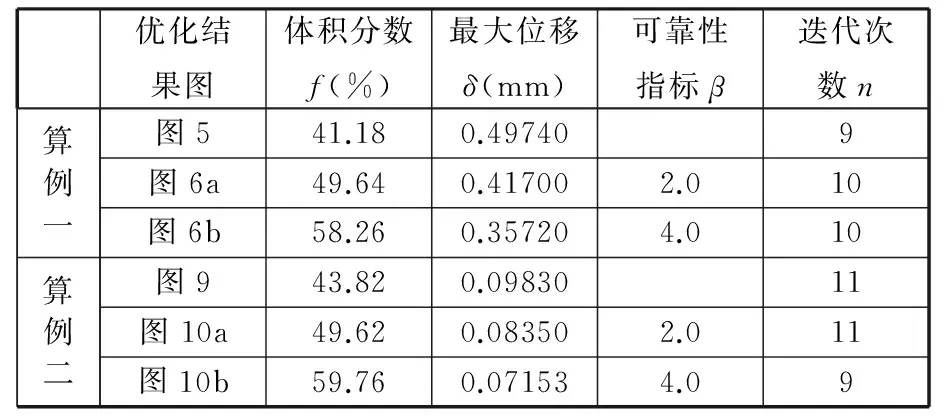
表1　優化結果對照表

5　結論

(1)利用響應面法近似逼近結構的隱式功能函數，極大簡化了因結構功能函數為隱式給可靠性分析帶來的困難。

(2)采用內外循環的策略，將可靠性分析和拓撲優化分開進行，避免了在拓撲優化過程中每步迭代都計算結構可靠性，而只需在拓撲優化結束時計算一次結構可靠性指標，極大減小了計算量同時提高了計算效率。

(3)算例一、算例二的分析結果表明:可靠性拓撲優化與確定性的拓撲優化相比，結構的體積分數僅有少量增加就能獲得較大的可靠度增長。該方法對于解決連續體可靠性拓撲優化是簡易可行的，可為解決工程實際的結構可靠性拓撲優化設計提供新思路和實用方法。

[1]Bendsoe M P，Kikuchi N.Generating Optimal Topologies in Structural Design Using a Homogenization Method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(1):197-224．

[2]Bendsoe M P,Sigmund O.Material Interpolation Schemes in Topology Optimization[J].Archive of Applied Mechanics,1999,69(9):635-654．

[3]Xie Y M,Steven G P.A Simple Evolutionary Procedure for Structural Optimization[J].Computers and Structures,1993,49(5):885-896．

[4]Querin O M,Yong V,Steven G P,et al.Computational Efficiency and Validation of Bi-directional Evolutionary Structural Optimization[J].Computer Methods in Applied Mechanics and Engineering,2001,189(2)：559-573．

[5]Sethian J A,Wiegmann A.Structural Boundary Design via Level Set and Immersed Interface Methods[J].Journal for Numerical Method in Engineering,2003,57(8):1177-1196．

[6]劉國梁,陳建軍,馬洪波.一種基于非概率可靠性的結構水平集拓撲優化[J].工程力學,2012,29(6)：58-62．

Liu Guoliang,Chen Jianjun,Ma Hongbo.Structural Topology Optimization for Non-probability Reliability in Level Set Method[J].Engineering Mechanics,2012,29(6):58-62.

[7]Kharmanda G,Olhohoff N,Mohamed A,et al.Reliability-based Topology Optimization[J].Structural and Multidisciplinary Optimization,2004,26(5)：295-307．

[8]鄺泳聰，歐陽高飛，張憲民． 基于可靠性的連續體結構拓撲優化設計[J]． 機械強度，2009，31 (4)：604-608．Kuang Yongcong,Ouyang Gaofei,Zhang Xianmin.Structural Topology Optimization of Continuous Structures Based on Reliability[J].Journal of Mechanical Strength,2009,31(4):604-608.

[9]Kwang S Y,Eom Y S,Park J Y,et al.Reliability-based Topology Optimization Using Successive Standard Response Surface Method[J].Finite Element in Analysis and Design,2011,47(7):843-849.

[10]Kwang S Y,Yong S E,Jae Y P,et al.Reliability-based Topology Optimization Using a Standard Response Surface Method for Three-dimensional Structures[J].Structural and Multidisciplinary Optimization,2011,43(2):287-295．

[11]李景奎，張義民．正態分布連續體結構可靠性拓撲優化設計[J].東北大學學報,2011,32(9):1303-1309．

Li Jingkui,Zhang Yimin.Reliability-based Topology Optimization Design of Normal Distribution Continuum Structure[J].Journal of Northeaster University,2011,32(9):1303-1309．

[12]李景奎,張義民.非正態分布連續體結構可靠性拓撲優化設計[J].機械工程學報,2012,48(3):153-158,Li Jingkui,Zhang Yimin.The Reliability-based Topology Optimization Design of Continuum Structure with Abnormal Distribution[J].Journal of Mechanical Engineering,2012,48(3):153-158．

[13]李好.基于變密度法的連續體結構拓撲優化方法研究[D].武漢:華中科技大學,2011.

[14]Chwail K,Semyung W.Reliability-based Topology Optimization with Uncertainties[J].Journal of Mechanical Science and Technology,2006,20(4):494-504．

[15]Maute K,Frangopol D M.Reliability-based Design of MEMS Mechanisms by Topology Optimization[J].Computers and Structures,2003,81(8):813-824．

[16]Seung J H,Seonho C.Reliability-based Topology Optimization of Geometrically Nonlinear Structures with Loading and Material Uncertainties[J].Finite Elements in Analysis and Design,2004,41(3):311-331．

[17]Zhang Bin,Wang X J,Sun X Y.Structural Topology Optimization Considering Stress and Reliability Constraints[J].Metalurgia International,2014,ⅪⅩ(2):59-63．

(編輯蘇衛國)

Reliability-based Topology Optimization of Implicit Performance Function Structure

Wu JinsongZhou Jinyu

Changzhou Key Laboratory of Equipment Remanufacturing Engineering, Jiangsu University of Technology,Changzhou,Jiangsu,213001

Considering the impacts of uncertain factors such as external loading,material property etc. on structural safety in engineering practice,the topology optimization design with the structural displacement reliability constrain was discussed.A mathematical of topology optimization was developed,where the minimization of compliance was taken as objective function,the relative densities of elements were taken as design variables,the material volume fraction and structural displacement reliability were taken as constraints.The response surface method was implemented to approximately approach its real performance function, for the situation that the structural performance function was implicit by using finite element numerical method.Then,the simple and efficient first order second moment method was used to obtain the structural displacement reliability.The strategy that inner loop was the deterministic topology optimization and the outer loop was to control the material volume fraction was implemented to carry out the reliability-based topology optimization of continuum structure.Finally,two numerical examples were given to be compared with the results of deterministic topology optimization showing that the design method is efficient and feasible.

reliability;topology optimization;implicit performance function;response surface method

2015-03-02

國家自然科學基金資助項目(51275221);江蘇省產學研聯合創新資金資助項目(BY2014038-04)

TB114;H122DOI：10.3969/j.issn.1004-132X.2015.16.013

吳勁松，男，1989年生。江蘇理工學院機械工程學院碩士研究生。研究方向為先進再制造技術與裝備。周金宇，男，1973年生。江蘇理工學院機械工程學院教授、博士、碩士研究生導師。