基于諧波原理的液體潤滑供油方式設計與實現

姬芬竹　杜發榮　郭雨琛　聶　磊

北京航空航天大學，北京，100191

基于諧波原理的液體潤滑供油方式設計與實現

姬芬竹杜發榮郭雨琛聶磊

北京航空航天大學，北京，100191

設計了基于諧波原理的液體潤滑供油系統，分析了其基本結構和供油機理。建立了彈性體的變形曲線理論模型和彈性體質點的振動模型；利用有限元軟件對彈性體變形進行了計算和分析，對儲油腔內潤滑油向摩擦表面的供應進行了仿真計算。計算結果表明：工作載荷作用下，彈性體沿徑向發生變形，彈性體質點產生振動，質點的振動使儲油腔內的潤滑油經連通油孔流向摩擦表面，實現了基于諧波原理的潤滑油供應，驗證了所設計的供油方式的有效性。

空間；液體潤滑；諧波原理；供油方式；彈性體

0　引言

在空間微重力環境下,傳統的地面液體潤滑系統不能正常工作，因此空間機械的潤滑方式主要為脂潤滑和固體潤滑[1-2]。液體潤滑效率高、壽命長，是未來長壽命航天器潤滑方式的主要發展方向[3]。多孔儲油器是最早應用于空間機械的液體潤滑設備,因其保持架微孔可儲油而得到廣泛應用[4-5]。但由于保持架微孔內儲油少,且散失與劣化后難以及時補充，因此壽命短，不能滿足長壽命航天器的需要[6-7]。

本文以諧波原理為理論基礎，提出一種液體潤滑供油方式。其主要特點是不設置傳統的液壓泵，利用彈性體變形和彈性體質點振動使儲油腔內的潤滑油流向摩擦表面。在分析其基本結構和供油機理的基礎上，通過對相互接觸零件的受力分析，建立彈性體變形模型和彈性體質點振動模型，分析了儲油腔內潤滑油向摩擦表面的供應。

1　基于諧波原理的液體潤滑供油方式

柔輪是諧波傳動的一個關鍵零件，在傳動過程中，作為薄壁彈性體的柔輪產生周期性變形，傳遞運動和動力[8-9]。本文基于諧波傳動基本原理,設計開發一種液體潤滑裝置,其基本結構和主要零件如圖1所示，主要有外圈、滾動體、彈性體、支撐體、連通油孔和儲油腔。

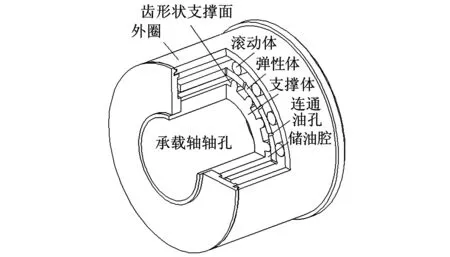
圖1　液體潤滑供油方式基本結構

該潤滑系統中,彈性體為一薄壁圓環類零件，位于滾動體和支撐體之間。外圈轉動時，滾動體在摩擦力作用下隨之旋轉;工作載荷(圖1中未標注)經外圈和滾動體作用于彈性體,使之產生徑向彎曲變形,同時彈性體質點有微小振動。彈性體的徑向變形和彈性體質點的振動使儲油腔內的潤滑油經連通油孔流向摩擦表面，實現潤滑油的供應。

2　理論模型

2.1彈性體變形模型

彈性體可看作薄壁圓環,薄壁圓環的變形可簡化為圓環平面的變形[10]。由材料力學知識可知,彎曲變形是彈性體的主要變形形式,且各點變形均很小,可采用薄壁環不伸長假設，即假定沿環的圓周方向彎曲中性面應變為零[10]。選取彈性體中性面的微小線元ab為研究對象，對線元ab的變形分析如圖2所示。

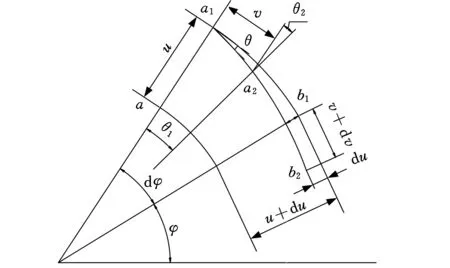
圖2　彈性體中性面微小線元變形分析

微小線元ab的徑向位移、切向位移分別用u和v表示。當線元由初始位置ab變化到終了位置a2b2時,我們可以把變形分為兩個階段。第一階段僅考慮徑向變形,線元從ab變化到a1b1,徑向位移則由u變化為u+du,若用φ表示線元ab的初始角,則其增量可表示為

(u+du)-u=(r+u)dφ-rdφ=udφ

(1)

式中,r為彈性體中性面的等效半徑,m;dφ為線元ab對應的中心角,rad。

第二階段僅考慮切向位移,線元由a1b1變化到a2b2,切向位移由v變化為v+dv,其線元增量為

(v+dv)-v=dv

(2)

根據薄壁圓環周向不伸長的假設,彈性體的周向增量為零,即udφ+dv=0,于是有

dv/dφ=-u

(3)

線元ab位移的法向轉角為

(4)

利用法向轉角對弧長的微分,即可求得彈性體線元ab的曲率變化率：

(5)

將式(3)代入式(5)，得

(6)

(7)

式中,M為彈性體的彎矩;E為材料彈性模量;Ix為彈性體慣性矩。

薄壁圓環彈性體的平衡方程為

(8)

式中,m為彈性體表面的分布力矩;qr為徑向分布載荷;qt為切向分布載荷。

由式(7)和式(8)消去M,得

(9)

對于本文研究的彈性體,m=0,qt=0,但在彈性體與支撐體接觸的包角2α范圍內作用有集中載荷F。若以徑向分布載荷qr代替集中載荷F,則受力分析見圖3。

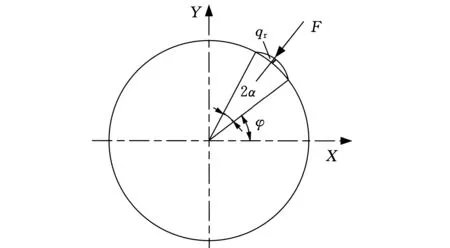
圖3　彈性體受力示意圖

假設彈性體與支撐體的齒形狀支撐面接觸包角為2α,齒形狀支撐面個數為n,取1/n圓周為研究對象。設α為任意小角度，于是有

傅里葉函數能將滿足一定條件的函數表示成三角函數或三角函數的積分的線性組合，因此采用傅里葉函數擬合變形函數應能取得較好的效果。把分布載荷qr以傅里葉函數展開為周期是2π/n的偶函數,即

(10)

式中,τ為二分之一周期,τ=π/n。

對式(10)積分并整理后可得到系數q0和qk:

于是

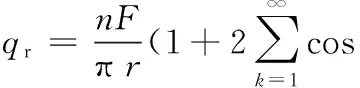
(11)

上式對φ求導后與式(9)合并,整理可得

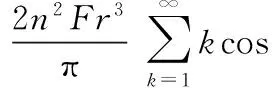
(12)

式(12)的解u可表示為

將u代入式(12),得

于是

(13)

式(13)給出了彈性體靜止時中性圓的徑向彎曲變形。可以看出,彈性體變形具有周期性變化的特點,可視為多個諧波的疊加。因此,在工作載荷作用下,當滾動體以角速度ω轉動時,彈性體圓環可形成波形運動。假設彈性體質點的初始位置與橫坐標軸的夾角為φ0,將φ=φ0+ωt代入式(13),可得任意時刻彈性體中性圓的徑向彎曲方程：

(14)

2.2彈性體質點振動模型

由式(14)取彈性體圓環的波形函數

u=u0cos[nk(φ0+ωt)]

(15)

式中,u0為彈性體的最大徑向變形。

將彈性體展開為OXY坐標系下的矩形梁,如圖4所示。由于彈性體處于微變形狀態,故有x=rφ0,代入式(15)并整理得

圖4　彈性體質點振動分析

(16)

在彈性體外圓表面上任取一點,設初始位置為P0,彎曲變形后的位置為P(對應的彎曲角為β)。于是,質點在X和Y方向的振動位移ux和uy分別為

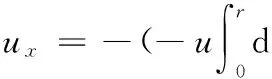
最大徑向位移u0比波長λ小很多,故β很小。因此,點P在X和Y方向的振動位移由下式近似計算：

對上式求導得質點P在X和Y方向的振動速度(切向和徑向的振動速度):

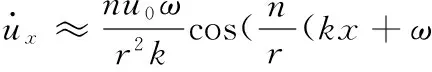
(17)

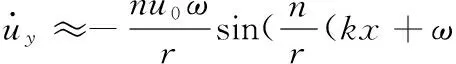
(18)

對振動速度求導即為振動加速度,不再列出。可以看出,彈性體質點切向和徑向的振動速度與滾動體個數n、彈性體半徑r、滾動體角速度ω以及最大徑向變形u0有關。

3　仿真計算與分析

由潤滑油物性參數可知,在本文所研究范圍內，潤滑油壓力較低,可以不考慮其壓縮性，即假定潤滑油是連續不可壓縮的[8]。

3.1彈性體變形和質點振動

振動分析時,振動位移反映振動幅度的大小，振動速度反映能量的大小,振動加速度反映沖擊力。彈性體質點的振動能量傳遞給儲油腔內的潤滑油，在振動沖擊力作用下實現潤滑油從儲油腔到摩擦面的供應。因此，通過對彈性體變形、彈性體質點振動速度和加速度的計算來研究儲油腔內潤滑油的流動在理論上是可行的。

利用有限元分析軟件Abaqus對彈性體變形和質點振動進行模擬計算，采用流固耦合技術對系統中潤滑油的流動進行仿真分析。分別建立固體域和流體域的計算模型，用直接耦合求解法在兩個模型間進行壓力和位移邊界條件的傳遞，即固體模型向流體模型傳遞位移和速度，并接受流體模型傳遞的壓力。采用三維實體六面體單元Solid185和四面體單元Solid187的混合單元(單元數為46 890,節點數為35 900),整體結構的有限元模型如圖5a所示。彈性體為圓(柱)環形零件，選用八節點單元Solid185,單元尺度為0.2～0.8 mm,模型見圖5b。

(a)整體結構有限元模型

(b)彈性體有限元模型圖5　結構件有限元模型

流體部分由初始真空區、初始滑油區和兩區域間的連通油孔組成，建立流體的有限體積模型如圖6所示，單元尺度為0.01～0.4 mm。

圖6　流體有限體積模型

取滾動體個數n=16,彈性體半徑r=17.5 mm,彈性體材料選用51CrV4彈簧鋼,彈性模量E=212 GPa,泊松比為0.28。仿真計算初始條件為:外圈轉速n=2400 r/min,工作載荷F=100 N在2α內均勻分布。選用航天用高黏度潤滑油，動力黏度為0.9 Pa·s。t1和t2時刻的彈性體中性圓在OXY坐標系下徑向變形見圖7。

圖7　彈性體中性圓徑向變形曲線示意圖

彈性體為薄壁圓環類零件，相對半徑而言,其厚度很小。因此,彈性體中性圓的變形曲線可看作其外圓或內圓的變形曲線，即彈性體變形曲線。由圖7可見,沿彈性體圓周方向的彎曲變形具有波形變化的特點,且具有近似周期性。彈性體的變形量u>0表示徑向伸長,彈性體的變形量u<0表示徑向壓縮。隨著時間的變化,變形沿X軸方向(彈性體圓周方向)移動。

圖8所示為某一時刻彈性體質點的振動速度和加速度變化曲線。可以看出,沿圓周方向彈性體質點具有不同的振動速度，即質點具有不同的能量；質點振動速度具有近似周期性變化的特點，一個周期內，振動速度有4個零點，零點的左右兩側分別對應正向速度和負向速度。同時，還可以看出，振動加速度亦具有正負值，說明沖擊力具有相反的兩個方向，分別為指向中心點和遠離中心點。加速度遠離中心點時，潤滑油從儲油腔供應到摩擦表面；指向中心點時，潤滑油從摩擦表面流回儲油腔。

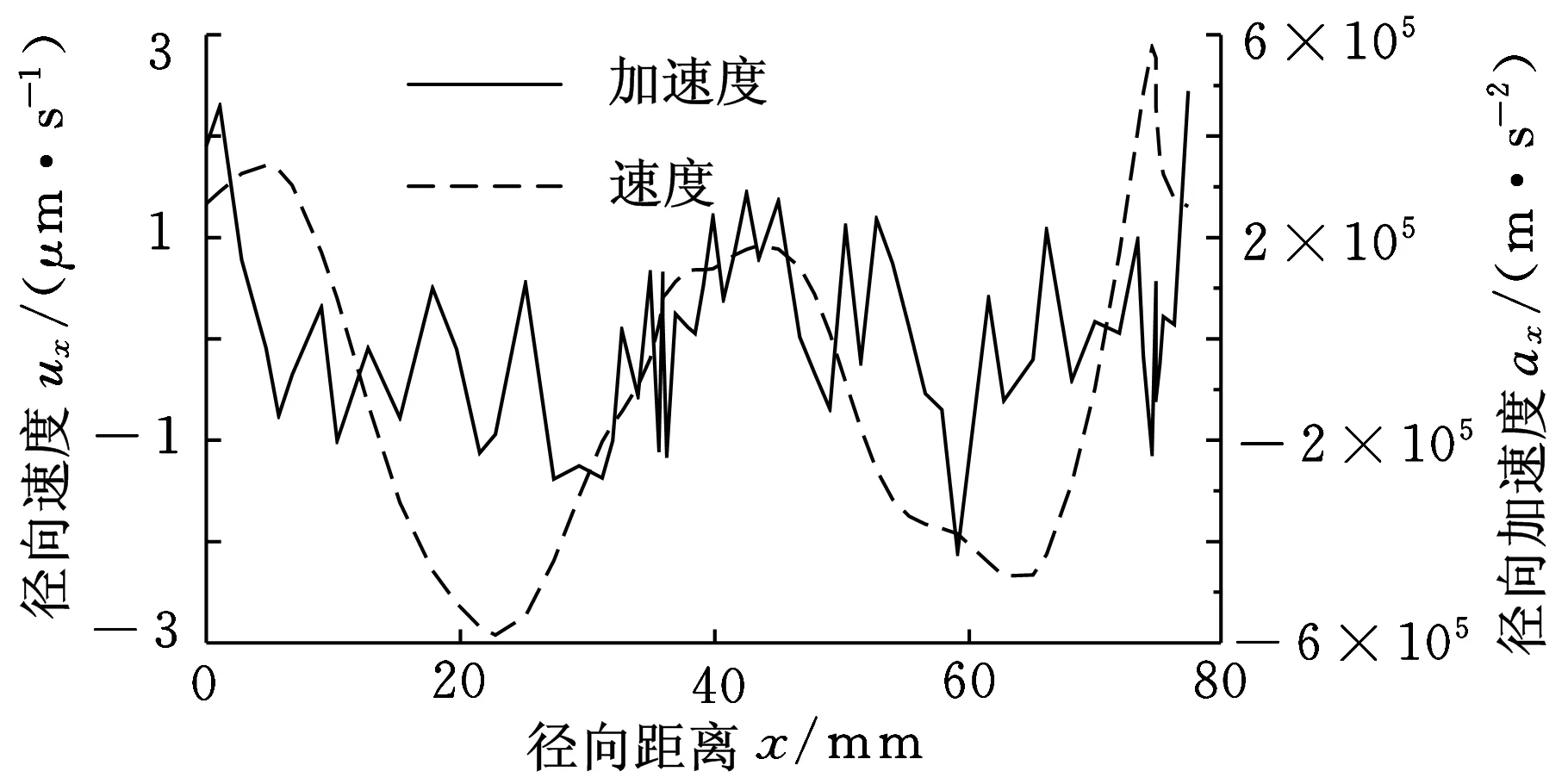
圖8　彈性體質點的徑向振動速度和加速度

3.2儲油腔內潤滑油向摩擦表面的供應

圖9為某一時刻潤滑油組分τ的分布云圖,可以看出,儲油腔(初始滑油區)內儲存的潤滑油經過連通油孔供應到需要潤滑的區域(初始真空區和滾動體表面)能夠實現基于諧波原理的潤滑油供應。

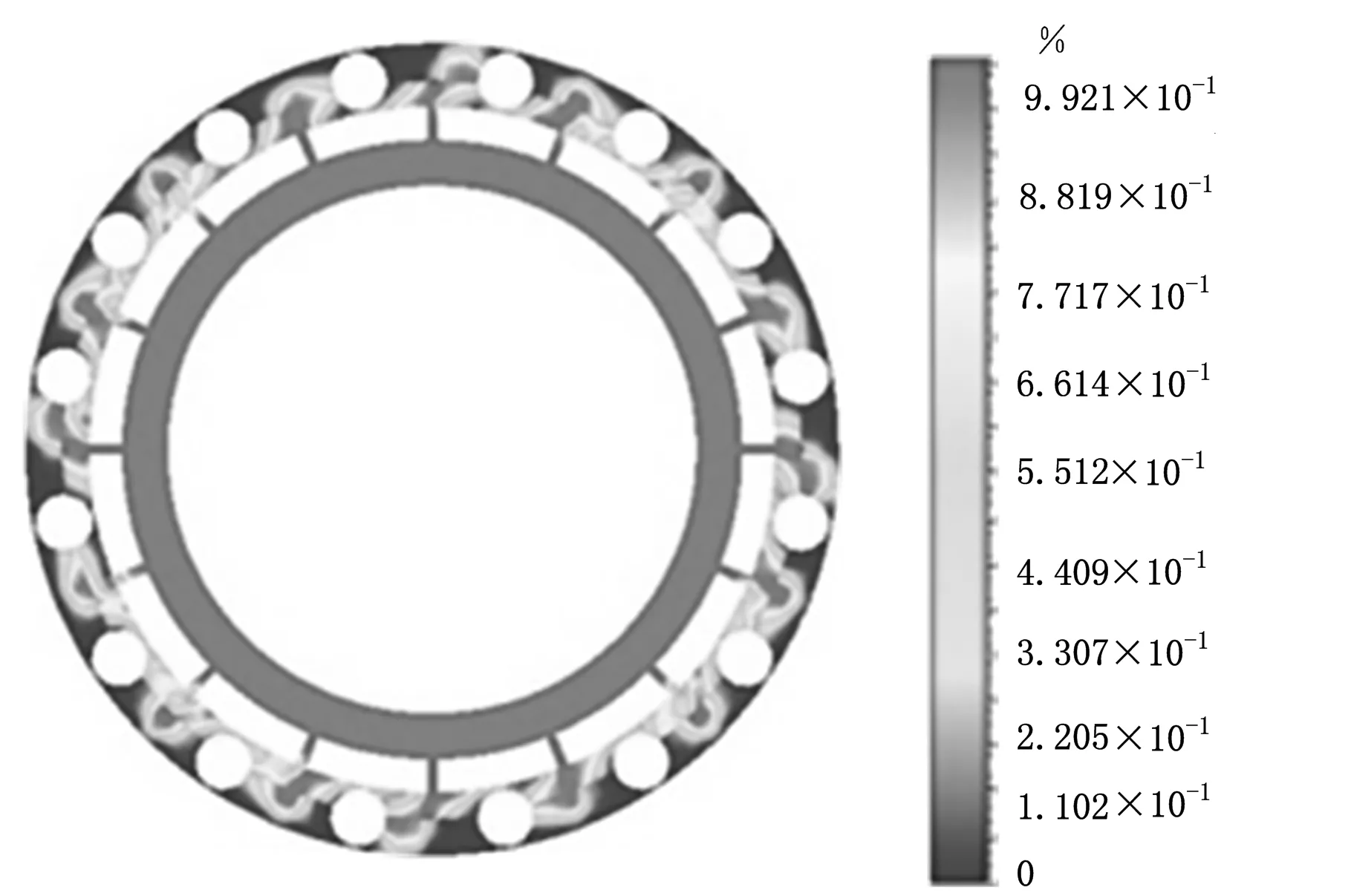
圖9　某一時刻潤滑油的組分分布

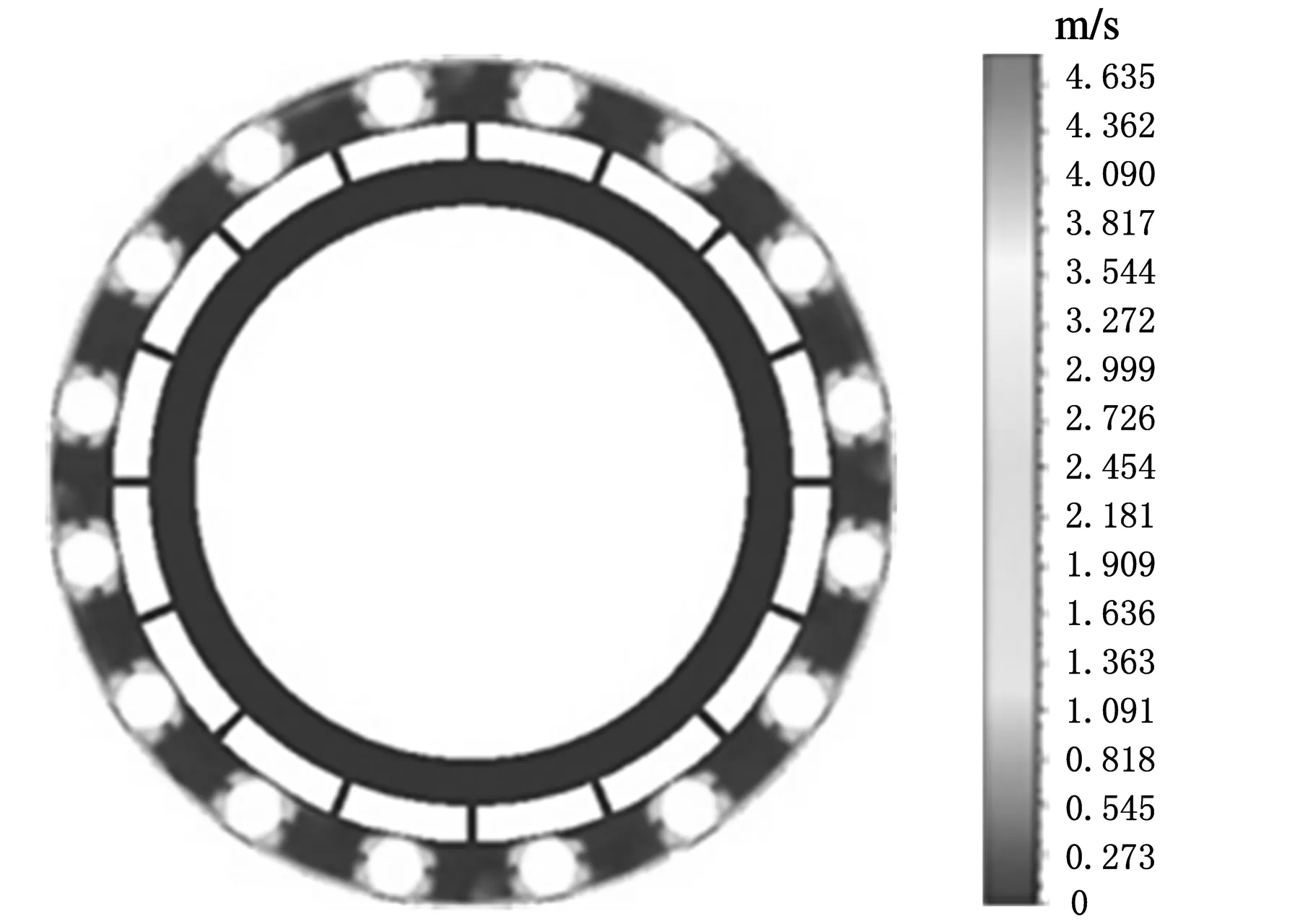
圖10　潤滑油速度分布示意圖

圖10為某一時刻潤滑油的速度云圖。可以看出,與滾動體接觸區域的潤滑油流速較高，最高達4.63 m/s(出現在滾動體與外圈的接觸面上);沿外圈內圓面圓周方向的潤滑油流速維持在3 m/s左右,其他區域的潤滑油流速較小。該潤滑油流速基本能夠滿足摩擦面對潤滑的需要。

圖11為連通油孔出口截面潤滑油壓力和油膜厚度隨時間變化曲線。可以看出，在很短時間內潤滑油壓力快速增大，說明儲油腔內的潤滑油經連通油孔供應到出口截面，但壓力的數值較小；此時出口截面的油膜厚度為零。之后隨著潤滑油壓力的進一步增大，油膜厚度逐漸增大；0.5～1.0 s時,潤滑油壓力基本上穩定在70.5 kPa,油膜厚度則緩慢增大,最大值為10 μm,能夠滿足摩擦面潤滑的需要。此外，系統中潤滑油壓力的最大值為70.5 kPa,遠小于其彈性模量1.7 GPa,說明本研究不考慮潤滑油可壓縮性的假設是合理的。

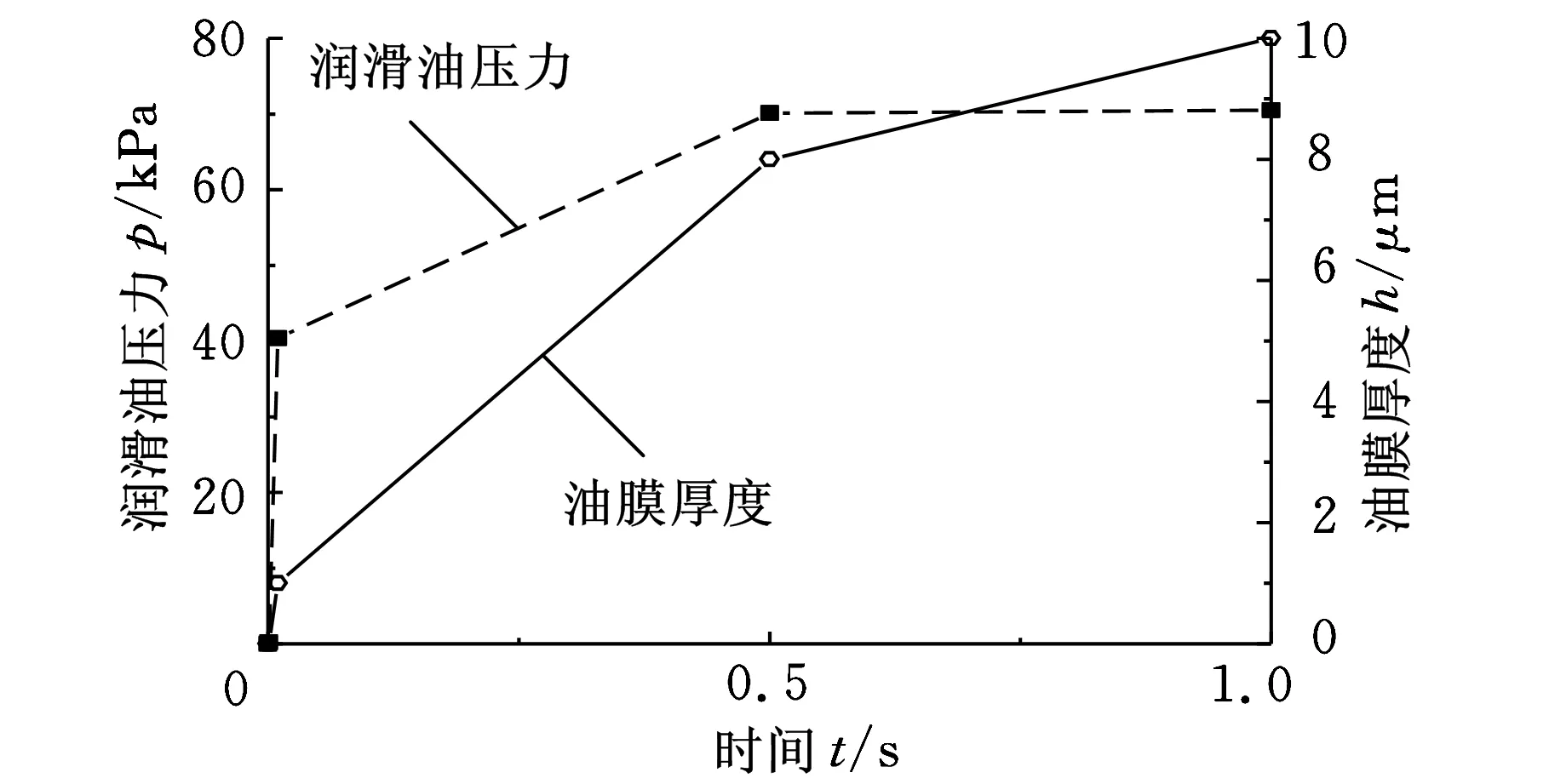
圖11　潤滑油壓力和流速

4　結論

(1)設計了液體潤滑儲油結構。外圈轉動時，工作載荷經滾動體作用于彈性體并使其產生彎曲變形和諧波振動；彈性體變形和質點振動使儲油腔內的潤滑油經連通油孔流向摩擦表面，實現液體潤滑。

(2)仿真結果驗證了所提出的液體潤滑供應方式的可行性，能夠實現基于諧波原理的潤滑油供應,開發了一種由系統內零件變形和質點振動供應潤滑油的新型潤滑方式。

[1]Vanhulsel A,Velasco F,Jacobs R,et al.DLC Solid Lubricant Coatings on Ball Bearings for Space Applications[J].Tribology International,2007,40:1186-1194.

[2]Kazuhisa Miyoshi.Solid Lubricants and Coatings for Extreme Environments:State-of-the-Art Survey,NASA/TM-2007-214668:7-15,E-15212[R].Cleveland,OH,United States:NASA Glenn Research Center,2007.

[3]王澤愛,陳國需.液體潤滑劑在航天器上的應用[J].潤滑油,2007,22(3)：37-42.

Wang Zeai,Chen Guoxu.Liquid Lubricants for Space Applications[J].Lubricating Oil,2007，22(3)：37-42.

[4]孫小波,王楓,葛世軍,等.航天長壽命軸承潤滑技術[J].軸承,2012(3):60-64.

Sun Xiaobo,Wang Feng,Ge Shijun,et al.Long-life Lubricating Technology for Bearings Used in Aerospace[J].Bearing,2012(3):60-64.

[5]姬芬竹.空間潤滑劑和液體潤滑系統的研究進展[J].潤滑與密封,2010,35(9):122-126.

Ji Fenzhu.Research Progress of Lubricants and Liquid Lubrication System in Space[J].Lubrication Engineering,2010,35(9):122-126.

[6]Sathyan K,Hsu H Y,Lee S H,et al.Long-term Lubrication of Momentum Wheels Used in Spacecraft-an Overview[J].Tribology International,2010,43(1):259-267.

[7]Ruan Bo.A Mixed Lubrication Model of Liquid/Gas Mechanical Face Seals[D].Atlanta:Georgia Institute of Technology,1995.

[8]李俊陽,王家序,周廣武,等.空間潤滑諧波減速器失效機理研究[J].摩擦學學報,2013,33(1):44-48.

Li Junyang,Wang Jiaxu,Zhou Guangwu,et al.Failure Mechanism of Harmonic Drivers for Space[J].Tribology,2013,33(1):44-48.

[9]Michael R.Life Test Failure of Harmonic Gears in a Two-axis Gimbal for the Mars Reconnaissance Orbiter Spacecraft[C]//Proceedings of the 38th Aerospace Mechanisms Symposium.Williamsburg,Virginia,United States,2006：6

[10]單輝祖.材料力學[M].北京:高等教育出版社,2010.

(編輯張洋)

Design and Implementation of Oil Supply Mode in Liquid Lubrication Based on Harmonic Principle

Ji FenzhuDu FarongGuo YuchenNie Lei

Beihang University,Beijing,100191

An oil-supply system in liquid lubrication system was designed based on harmonic principle. The basic structure and oil- supply mechanism were analyzed. The elastomer was one of the main parts. The deformation and particle vibration of the elastomer were as the key factors for oil supplying. The theoretical modes were founded on deformation curve and particle vibration trail of the elastomer. The elastomeric deformation was calculated and analyzed utilizing the finite element software.And the simulation analysis was done for the oil flowing from storage chamber to friction surfaces. The calculation results show that: the radial (bending) deformation of elastomer is emerged under the working load; and the particle vibration is occurred along the radial and circumference directions; the deformation and vibration make the oil flow to friction surfaces from the oil cavity through holes. So the oil supply mode in view of the harmonic principle can be achieved. The effectiveness of this oil supply mode was verified.

space; liquid lubrication; harmonic principle; oil supply mode; elastomer

2013-09-27

國家自然科學基金資助項目(51175018);航空科學基金資助項目(2011ZA51);北京市自然科學基金資助項目(3113030)

TH13< class="emphasis_italic">DOI

：10.3969/j.issn.1004-132X.2015.02.018

姬芬竹,女,1963年生。北京航空航天大學交通科學與工程學院副教授。主要研究方向為發動機熱管理和潤滑系統。獲發明專利2項。發表論文30余篇。杜發榮,男,1963年生。北京航空航天大學交通科學與工程學院副教授。郭雨琛，男，1988年生。北京航空航天大學交通科學與工程學院研究生。聶磊，男,1987年生。北京航空航天大學交通科學與工程學院研究生。