管道熱屈曲動力過程數(shù)值模擬

王立忠，王寬君，施若葦

(浙江大學(xué) 建筑工程學(xué)院，浙江 杭州 310058)

管道熱屈曲動力過程數(shù)值模擬

王立忠，王寬君，施若葦

(浙江大學(xué) 建筑工程學(xué)院，浙江 杭州 310058)

運(yùn)輸高溫高壓油氣的海底管道會發(fā)生整體熱屈曲現(xiàn)象。管道熱屈曲過程中可能會產(chǎn)生平衡狀態(tài)的躍遷(snap-through)，且這樣的躍遷過程必然會伴隨著動力響應(yīng)。管道熱屈曲動力過程中側(cè)向彈出的速度以及軸向縮進(jìn)的速度對管土相互作用參數(shù)的取值有很大影響，然而關(guān)于管道熱屈曲動力過程的研究卻很少。本文給出了數(shù)值模擬過程中管道系統(tǒng)阻尼值和升溫速率的確定方法，研究了管道初始幾何缺陷以及海床參數(shù)對管道熱屈曲動力過程的影響。

管道熱屈曲；動力過程；阻尼值；升溫速率；初始幾何缺陷；海床參數(shù)

高溫高壓管道在內(nèi)部溫度、壓力荷載以及海床軸向約束的作用下會產(chǎn)生巨大的軸力，當(dāng)軸力達(dá)到一定值時管道就會發(fā)生類似于歐拉梁失穩(wěn)的現(xiàn)象，如圖1所示，管道工程中把這樣的失穩(wěn)現(xiàn)象稱為管道整體熱屈曲(Global pipeline buckling)。如圖2所示，對于理想的平直管道，一定的溫度荷載對應(yīng)著兩個平衡狀態(tài)(曲線1)：①B點(diǎn)所示平衡狀態(tài)，其變形幅值較小且軸力沒有充分釋放，屬于不穩(wěn)定平衡狀態(tài)，②C點(diǎn)所示平衡狀態(tài)，其變形幅值很大且軸力得到充分釋放，屬于穩(wěn)定的平衡狀態(tài)[1]。在微小擾動下，處于B點(diǎn)平衡狀態(tài)的管道會發(fā)生失穩(wěn)現(xiàn)象，突然形變(snap- through)至C點(diǎn)的平衡狀態(tài)。對于初始幾何缺陷較小的情況，管道的失穩(wěn)過程也存在突然形變的現(xiàn)象，如曲線2中A點(diǎn)至D點(diǎn)；當(dāng)初始幾何缺陷增大后，突變現(xiàn)象消失，溫度荷載與屈曲狀態(tài)呈如曲線3所示的單調(diào)函數(shù)。借鑒鋼結(jié)構(gòu)穩(wěn)定理論[2]中對軸心受壓構(gòu)件失穩(wěn)的定義，管道熱屈曲模式可以分為如下兩種：①跳躍型(曲線2)：管道在失穩(wěn)過程中會發(fā)生形變上不連續(xù)的躍遷，與軸心受壓構(gòu)件的躍越失穩(wěn)模式[2]相似；②分岔型(曲線3)：管道的荷載形變曲線沒有極值點(diǎn)，但平衡狀態(tài)會發(fā)生明顯改變(平衡狀態(tài)的分岔)，與軸心受壓構(gòu)件的穩(wěn)定分岔失穩(wěn)模式[2]類似。需要注意的是穩(wěn)定分岔失穩(wěn)的定義是針對無缺陷軸心受壓構(gòu)件，而本文中定義的分岔型失穩(wěn)是針對有缺陷的管道。在實(shí)際工程設(shè)計(jì)中需要避免管道發(fā)生跳躍型屈曲失穩(wěn)，因?yàn)樘S型屈曲失穩(wěn)會使管道受到額外的動力荷載而更容易發(fā)生破壞。

圖2 管道熱屈曲溫度幅值曲線Fig. 2 Temperature rise versus bucking amplitude

目前關(guān)于管道熱屈曲的數(shù)值模擬大多采用靜力方法(Static- implicit)，這對于分岔型屈曲是適用的，但對于跳躍型屈曲，靜力算法忽略掉了管道失穩(wěn)過程中的有關(guān)狀態(tài)量，譬如管道彈出的速度。同時，采用靜力算法計(jì)算跳躍型屈曲失穩(wěn)時，收斂性很差，特別當(dāng)管道初始缺陷較小、管道變形的突變量較大時，靜力算法基本上無法收斂。趙天奉[3]采用了改進(jìn)的Riks算法，可以得到管道后屈曲狀態(tài)，但也無法模擬管道熱屈曲過程中的動力響應(yīng)。Liu等[4]基于ABAQUS采用顯式動力算法(Dynamic- explicit)分析了管道整體熱屈曲過程，并指出顯式動力算法可以模擬管道熱屈曲過程中的動力響應(yīng)。然而，顯式算法需要很小的時間增量步，其時間增量步取決于模型的最高固有頻率而與荷載的類型和持續(xù)時間無關(guān)，通常模擬需要取一萬到一百萬個增量步。

管道升溫至臨界屈曲溫度的過程顯然不可能在幾秒鐘完成，根據(jù)管道離熱源(油井)的距離通常需要幾分鐘到幾個小時不等[5]。管道的屈曲失穩(wěn)過程相對于管道整個升溫過程是短暫的，大多數(shù)時間內(nèi)管道處于靜力狀態(tài)，只有在屈曲失穩(wěn)的瞬間存在動力響應(yīng)。如果采用顯式算法，由于受最小時間增量步的限制，需要的時間增量步數(shù)量巨大。然而，采用隱式動力算法(Dynamic- implicit)沒有最小時間增量步的限制，對于動力響應(yīng)以外的時間段可以提高時間增量步大小，提高了計(jì)算效率。因此，本文將基于ABAQUS采用隱式動力算法模擬管道熱屈曲過程中的動力響應(yīng)。

1 數(shù)值模型建立

1.1模型基本參數(shù)

管道發(fā)生屈曲時管道與海床相互作用的長度較小，摩擦力對兩端幾乎沒有影響，兩端采用固支約束不會對管道屈曲產(chǎn)生影響。所以本文數(shù)值模擬采用的管道長度為1 000 m，管道末端為固支約束。管道中部設(shè)有正弦函數(shù)形狀的側(cè)向初始幾何缺陷，缺陷長度取100 m，缺陷幅值為vom，具體管道的有限元模型如圖3所示。管道的幾何和力學(xué)參數(shù)如表1所示，其中A是管道截面積，I是截面轉(zhuǎn)動慣量，E是管道材料的彈性模量，α是管道材料的膨脹系數(shù)，w是管道的有效重度，D是管道直徑。

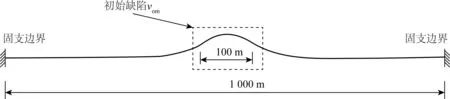
圖3 有限元模型Fig. 3 The finite element model

表1 管道參數(shù)Tab. 1 Pipeline parameters

管道采用B21H單元，即線性的二維梁單元，管道單元長度均為1 m，這樣設(shè)置可以統(tǒng)一管土相互作用參數(shù)。采用非線性土彈簧模擬管土側(cè)向和軸向相互作用，管土相互作用模型如圖4所示。軸向管土相互作用采用雙線性模型，滑移距離s取0.003 m。側(cè)向管土相互作用分別采用雙線性和三線性模型并進(jìn)行對比分析。根據(jù)White和Cheuk[6]的建議，滑移距離s(s1)和s2分別為0.1D和0.25D左右，取s=s1=0.06 m，s2=0.24 m。

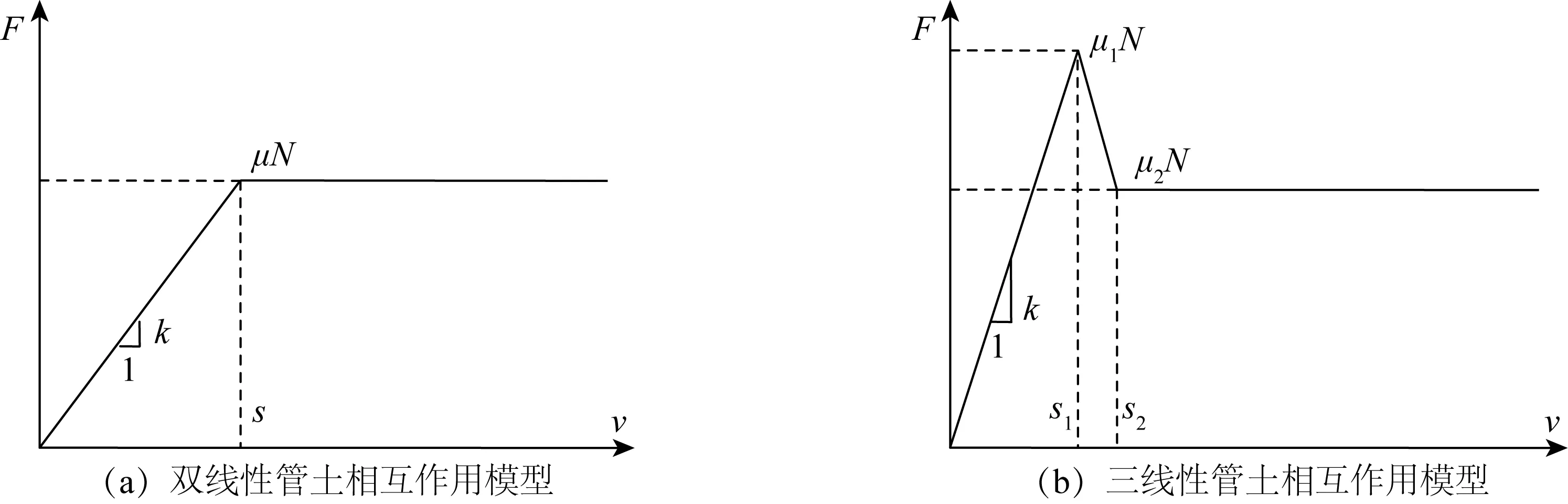
圖4 管土相互作用模型Fig. 4 Soil- pipe interaction model

1.2阻尼值和升溫速率的選取

(1)阻尼值的選取

在ABQUS隱式動力算法中，采用瑞利阻尼：

式中:α和β是由用戶自定義的參數(shù)，M為系統(tǒng)質(zhì)量，K為剛度矩陣。瑞利阻尼屬于數(shù)值阻尼，沒有物理意義。在數(shù)值試算中，取β=0；初始幾何缺陷為vom=1m；管土相互作用為雙線性模型，側(cè)向摩擦系數(shù)取μy=1，軸向摩擦系數(shù)取μx=0.5；升溫速率為0.01°C/s。

由于目前尚無管道熱屈曲過程中阻尼值選取的相關(guān)資料，DNV- RP- F105規(guī)范給出了管道渦激振動時阻尼比的取值方法[7]：

圖5 不同阻尼值下的管道中點(diǎn)側(cè)向位移與溫度的關(guān)系Fig. 5 Lateral displacement versus temperature of pipeline midpoint for different damping values

阻尼比是當(dāng)前阻尼值與臨界阻尼值的比值。任何一個振動系統(tǒng)，當(dāng)阻尼增加到一定程度時，物體的運(yùn)動是非周期性的，當(dāng)阻力使振動物體剛能不作周期性振動而又能最快地回到平衡位置的情況，物體振動連一次都不能完成時的阻尼值稱為“臨界阻尼”。方程(2)中，ζT是系統(tǒng)總的的阻尼比，ζstr是結(jié)構(gòu)阻尼比，ζsoil為土的阻尼比，ζh為水的阻尼比。ζstr根據(jù)管道配重的不同，取值范圍約為為0.005～0.02，ζsoil根據(jù)土的性質(zhì)不同，取值范圍約為0.01～0.03，通常ζh取0。對于渦激振動，管道懸跨段不與土體接觸，而管道側(cè)向屈曲過程中整個管道都與土體接觸，所以土體阻尼比需要相應(yīng)增大。另一方面，瑞利阻尼模型對于大阻尼系統(tǒng)(阻尼大約超過臨界阻尼的10%)是不可靠的[8]。因此，本文取阻力比為ζT=0.05。

為了確定自定義參數(shù)α的值，圖5給出了不同α情況下管道中點(diǎn)位移vo與溫度T的關(guān)系曲線。當(dāng)α=0.5和5時，管道失穩(wěn)時會發(fā)生動力抖動，之后逐漸接近靜力計(jì)算結(jié)果；當(dāng)α=20時，管道不存在動力抖動且變形值比靜力計(jì)算結(jié)果小，屬于過阻尼；當(dāng)α=10時，管道動力計(jì)算結(jié)果與靜力計(jì)算結(jié)果十分接近，此時的阻尼值為臨界阻尼。根據(jù)阻尼比的定義可以得到本文模型的阻尼值α=0.05×10 =0.5。

(2)升溫速率

管道系統(tǒng)的熱傳遞受很多因素影響，譬如石油的溫度，油氣與管道之間的熱傳導(dǎo)系數(shù)，管道絕熱層厚度，管道所處的環(huán)境溫度等。根據(jù)Alves 等[5]的算例，熱源處管道從0°C到50°C的平均升溫速率約為0.12°C/s，典型的管道升溫速率在0.01°C/s的數(shù)量級。

在數(shù)值試算中，管土側(cè)向相互作用取雙線性模型，側(cè)向摩擦系數(shù)μy=1，軸向摩擦系數(shù)μx=0.5；阻尼值取α=0.5；初始缺陷分別取vom=1 m；管道的升溫速率分別取0.01，0.1，1和10°C/s。

圖7 升溫速率為0.1和0.01°C/s時管道中點(diǎn)側(cè)向速度對比Fig. 7 Lateral velocity versus temperature of pipeline midpoint for 0.1 and 0.01°C/s

從圖6中可以看出，對于0.1°C/s和1°C/s的升溫速率，管道位移曲線基本吻合，且管道屈曲后側(cè)向彈出的速度會被系統(tǒng)阻尼消耗而逐漸減小至零。然而對于10°C/s的升溫速率，管道位移與其它兩種升溫速率相比已有明顯變化，且管道屈曲后側(cè)向速度會一直存在，數(shù)值計(jì)算不收斂。1°C/s的升溫速率可以得到收斂的計(jì)算結(jié)果，但其側(cè)向速度峰值比0.1°C/s時偏大約40%。

圖7對比了0.01°C/s和0.1°C/s升溫速率情況下管道中點(diǎn)的側(cè)向速度。升溫速率為0.01°C/s時，管道的峰值速度約為1.61 m/s；而升溫速率為0.1°C/s時，管道的峰值速度約為1.69 m/s，兩者相差不超過5%。然而采用0.01°C/s升溫速率所耗費(fèi)的計(jì)算時間是0.1°C/s的10倍，因此，本文數(shù)值計(jì)算中采用升溫速率為0.1°C/s是合適的。

2 參數(shù)分析

2.1初始幾何缺陷的影響

管土側(cè)向相互作用采用雙線性模型，側(cè)向摩擦系數(shù)取μy=1，軸向摩擦系數(shù)取μx=0.5。對于vom=0.5～10 m的初始幾何缺陷，管道中點(diǎn)軸力po、側(cè)向位移vyo與溫度T的關(guān)系如圖8所示。初始幾何缺陷vom=0.5和1 m時，管道發(fā)生跳躍型屈曲失穩(wěn)，其它初始缺陷情況下管道發(fā)生分岔型屈曲失穩(wěn)。管道屈曲失穩(wěn)前處于軸向受壓狀態(tài)，軸力隨溫度升高而增長，位移基本為零；管道屈曲失穩(wěn)后處于壓彎狀態(tài)，位移vyo迅速增長，軸力得到釋放。管道的臨界屈曲溫度Tcr隨其初始缺陷vom的變大而逐漸減小；但初始缺陷持續(xù)增大時，管道臨界屈曲溫度Tcr不會持續(xù)減小而是穩(wěn)定在23°C左右，如圖9所示。

圖8 不同初始缺陷下管道中點(diǎn)軸力和位移的變化Fig. 8 The influence of different initial geometric imperfection: (a) axial force, (b) displacement

圖9 管道屈曲失穩(wěn)臨界溫度與初始缺陷的關(guān)系 Fig. 9 The critical temperature versus initial geometric imperfection

管道中點(diǎn)側(cè)向速度uyo在升溫過程中的變化如圖10所示。初始缺陷vom=2 m時，管道在整個升溫過程中不發(fā)生動力響應(yīng)，側(cè)向速度基本為零；當(dāng)vom=1 m時，管道發(fā)生失穩(wěn)時的最大側(cè)向速度約為1.8 m/s,vom=0.5 m時管道最大側(cè)向速度約為5 m/s，可見管道熱屈曲失穩(wěn)時的側(cè)向速度隨初始缺陷的減小而增大。升溫過程中，離管道中點(diǎn)50 m處的軸向運(yùn)動速度ux50如圖11所示。管道屈曲失穩(wěn)時，軸向速度的數(shù)值比側(cè)向速度小一個數(shù)量級，軸向速度也隨初始缺陷的減小而增大。可以看出，管道初始缺陷越小管道發(fā)生跳躍型屈曲失穩(wěn)時的動力響應(yīng)越明顯。

管道失穩(wěn)時的側(cè)向與軸向速度大小對管土相互作用參數(shù)的取值有著很大的影響。土體的不排水抗剪強(qiáng)度su跟應(yīng)變率有關(guān)，且管道運(yùn)動速度影響海床土體中孔隙水壓力的產(chǎn)生和消散，從而影響土體抗力的大小[9]。通過基于動力算法的有限元計(jì)算能得到管道屈曲時的側(cè)向和軸向速度，從而為管土相互作用試驗(yàn)和數(shù)值模擬提供參數(shù)，確定管土相互作用加載速率的選取范圍。

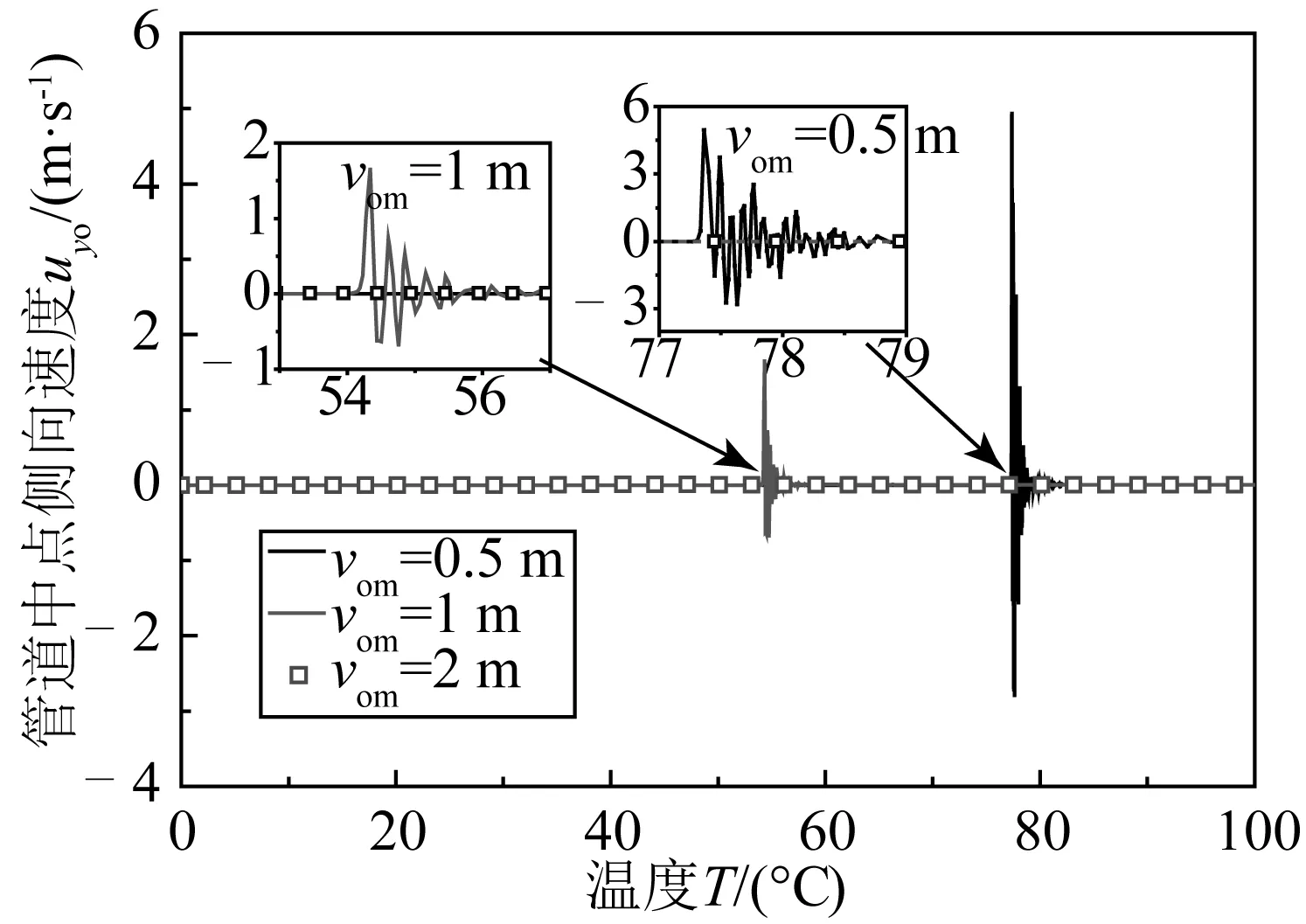
圖10 管道中點(diǎn)側(cè)向速度Fig. 10 Lateral velocity of pipeline midpoint

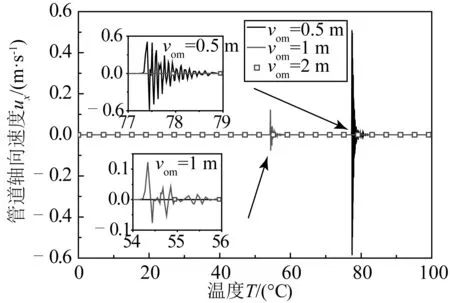
圖11 離管道中點(diǎn)50 m處的軸向速度Fig. 11 Axial velocity of the point 50 meters away from pipe midpoint

隨著初始缺陷的減小，管道失穩(wěn)時的突變量會逐漸增大。當(dāng)vom<1 m后，靜力算法通常只能計(jì)算到屈曲突變之前，隨后即無法收斂，不能得到屈曲突變的過程和后屈曲狀態(tài)。因?yàn)榇藭r管道屈曲失穩(wěn)前后所對應(yīng)的兩個平衡狀態(tài)的形變量相差過大，數(shù)值計(jì)算無法從前屈曲的平衡狀態(tài)迭代到后屈曲的平衡狀態(tài)。然而，無論初始缺陷值取多小動力算法都不會產(chǎn)生不收斂的問題，且動力算法可以得到管道熱屈曲過程中側(cè)向彈出和軸向縮進(jìn)的速度。因此，動力算法更適用于對管道熱屈曲的數(shù)值模擬，特別是初始缺陷較小且管道發(fā)生跳躍型失穩(wěn)的情況。

2.2管土相互作用參數(shù)影響

管土側(cè)向和軸向相互作用都采用雙線性模型，軸向摩擦系數(shù)取定值μx=0.5，對側(cè)向摩擦系數(shù)μy進(jìn)行參數(shù)分析。從圖12和13中可以看出，海床側(cè)向抗力減小會導(dǎo)致管道臨界屈曲溫度減小，且管道屈曲失穩(wěn)時的動力響應(yīng)會減弱；相同溫度情況下，海床側(cè)向抗力減小會導(dǎo)致管道屈曲幅值增大。以初始缺陷vom=1 m為例，側(cè)向摩擦系數(shù)為1.5和1時，管道會發(fā)生跳躍型失穩(wěn)；但當(dāng)側(cè)向摩擦系數(shù)減小到0.5時，管道發(fā)生分岔型失穩(wěn)。當(dāng)vom=2 m，側(cè)向摩擦系數(shù)為1和1.5時，管道發(fā)生分岔型失穩(wěn)；但當(dāng)側(cè)向摩擦系數(shù)達(dá)到3時管道會發(fā)生跳躍型失穩(wěn)。因此，管道屈曲失穩(wěn)的類型不僅與初始缺陷有關(guān)還與海床側(cè)向抗力有關(guān)，海床側(cè)向抗力越大管道越容易發(fā)生跳躍型失穩(wěn)。

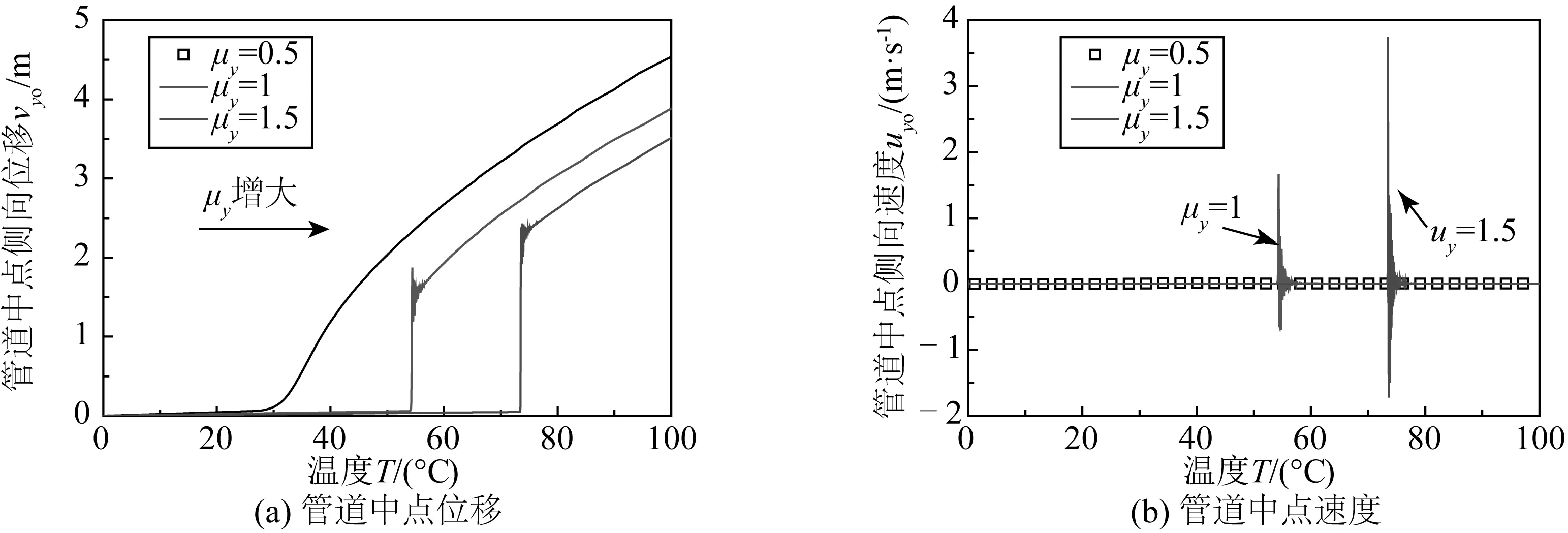
圖12 初始缺陷vom=1 m時管道中點(diǎn)側(cè)向位移和速度Fig. 12 Lateral displacement and velocity of pipeline midpoint for vom=1 m

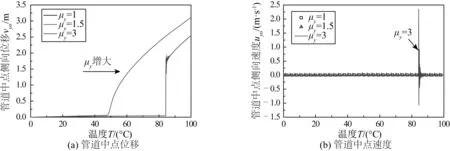
圖13 初始缺陷vom=2 m時管道中點(diǎn)側(cè)向位移和速度Fig. 13 Lateral displacement and velocity of pipeline midpoint for vom=2 m

管土側(cè)向和軸向相互作用都采用雙線性模型，側(cè)向摩擦系數(shù)取定值μy=1，對軸向摩擦系數(shù)μx進(jìn)行參數(shù)分析。從圖14和圖15中可以看出，軸向摩擦系數(shù)對管道的臨界屈曲溫度基本沒有影響，但管道的后屈曲變形幅值隨μx的提高而減小。管道發(fā)生熱屈曲以后，管道平直段會有向屈曲段擠進(jìn)的趨勢(feed- in)，軸向摩擦力約束了管道平直段的軸向擠進(jìn)從而抑制了屈曲變形。從圖14中可以看出，對于跳躍型屈曲，軸向摩擦系數(shù)越大，管道發(fā)生屈曲失穩(wěn)時的動力響應(yīng)越明顯，管道側(cè)向彈出的速度越大。然而，提高軸向摩擦力并不會改變管道屈曲失穩(wěn)的模式，對于vom=2 m的情況(圖15)，軸向摩擦系數(shù)從0.5增長到1時，管道的屈曲失穩(wěn)類型一直為分岔型失穩(wěn)。

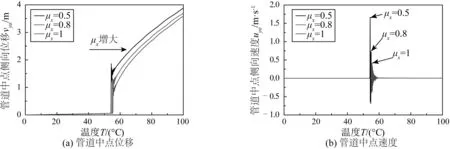
圖14 初始缺陷vom=1 m時管道中點(diǎn)側(cè)向位移和速度Fig. 14 Lateral displacement and velocity of pipeline midpoint for vom=1 m

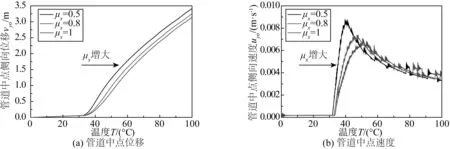
圖15 初始缺陷vom=2 m時管道中點(diǎn)側(cè)向位移和速度Fig. 15 Lateral displacement and velocity of pipeline midpoint for vom=2 m

海床對管道的軸向摩擦力影響管道后屈曲狀態(tài)，但對管道前屈曲狀態(tài)和臨界屈曲溫度沒有影響。這是因?yàn)楣艿狼疤幱谳S向壓縮狀態(tài)，軸向摩擦力不發(fā)揮作用；一旦管道發(fā)生屈曲失穩(wěn)形成屈曲段，管道平直段會產(chǎn)生向屈曲段擠進(jìn)的趨勢，此時軸向摩擦力開始發(fā)揮作用。軸向摩擦力越大對管道軸向擠進(jìn)的約束越大，從而管道屈曲段變形越小。

下面進(jìn)行三線性管土相互作用模型的分析，相關(guān)參數(shù)見表2。在三線性管土相互作用模型中，Hbrk=μy1w表示管道破土?xí)r海床對管道的最大抗力(break out resistance)，Hres=μy2w表示管道破土后海床對管道的殘余抗力(residual resistance)；其中μy1和μy2是海床與管道之間的摩擦系數(shù)，w是管道有效重度。三線性管土作用模型通常用來模擬“輕管”的側(cè)向管土相互作用過程。所謂“輕管”就是Vmax/V> 2.5的管道[10]，其中Vmax指管道整個生命周期中海床對其最大抗力，V是目前海床對管道的豎向抗力。Vmax/V越大會導(dǎo)致μy2/μy1越大。

表2 三線性管土相互作用參數(shù)Tab. 2 Parameters of trilinear response for soil- pipe interaction

從圖16中可以看出，μy1越大管道臨界屈曲溫度越高，管道屈曲失穩(wěn)時的動力響應(yīng)也會越明顯，管道側(cè)向彈出的速度越大。然而，管道屈曲后的幅值幾乎不受μy1的影響。因?yàn)榇藭r管道位移已經(jīng)相對較大，管土相互作用已經(jīng)進(jìn)入三段線的最后一段，此時海床側(cè)向抗力為Hres=μy2w，所以管道后屈曲變形是由μy2控制的。

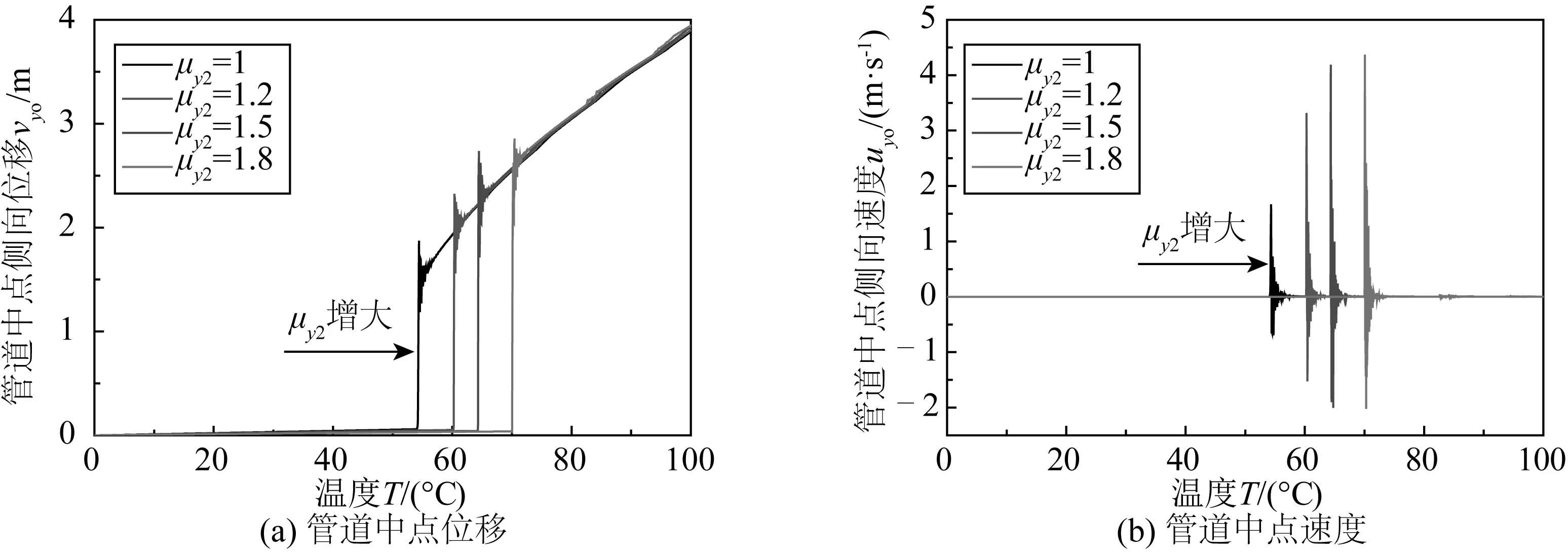
圖16 初始缺陷vom=1 m時管道中點(diǎn)側(cè)向位移和速度Fig. 16 Lateral displacement and velocity of pipeline midpoint for vom=1 m

從圖17可以看出，μy1影響管道的屈曲失穩(wěn)類型。當(dāng)μy1從1變?yōu)?.2時，管道從分岔型失穩(wěn)轉(zhuǎn)變成跳躍性失穩(wěn)。隨著μy1增大，管道的動力響應(yīng)越來越明顯，管道彈出的速度也越來越大。相對于雙線性的管土相互作用模型，三線性管土相互作用模型更準(zhǔn)確地模擬了“輕管”的管土相互作用模式。由于三線性管土相互作用存在峰值抗力和抗力跌落的過程，管道更容易發(fā)生跳躍型失穩(wěn)。

3 結(jié) 語

本文基于ABAQUS有限元軟件采用隱式動力算法(Dynamic- implicit)，對管道熱屈曲過程進(jìn)行了數(shù)值模擬，并給出了阻尼取值和升溫速率的合理取值。詳細(xì)結(jié)論如下：

1)隱式動力算法能模擬管道熱屈曲過程中的動力響應(yīng)，得到管道屈曲失穩(wěn)過程中的側(cè)向彈出和軸向縮進(jìn)速度，從而為管土相互作用模型提供參數(shù)。

2)管道的熱屈曲失穩(wěn)過程分為兩種：跳躍型失穩(wěn)和分岔型失穩(wěn)。管道發(fā)生跳躍型失穩(wěn)時會產(chǎn)生動力響應(yīng)，發(fā)生分岔型失穩(wěn)時沒有動力響應(yīng)。

3)管道初始缺陷越小越容易發(fā)生跳躍型失穩(wěn)，反之則發(fā)生分岔型失穩(wěn)。管道的臨界屈曲溫度隨其初始缺陷的增大而逐漸減小；但初始缺陷持續(xù)增大，管道臨界屈曲溫度不會持續(xù)減小而是穩(wěn)定在某一溫度。管道初始缺陷越小，其屈曲失穩(wěn)過程中的動力響應(yīng)越明顯，管道側(cè)向彈出的速度和軸向縮進(jìn)的速度越快。

4)海床對管道的側(cè)向抗力是除初始缺陷以外影響管道熱屈曲類型的另一個重要因素。在雙線性管土相互作用模型中，海床對管道側(cè)向抗力越大，管道越可能發(fā)生跳躍型失穩(wěn)，失穩(wěn)時的動力響應(yīng)也越大。在三線性管土相互作用模型中，管道破土?xí)r海床最大抗力Hbrk對管道熱屈曲的動力響應(yīng)影響很大，Hbrk越大管道越容易發(fā)生跳躍型失穩(wěn)，且失穩(wěn)時的動力響應(yīng)也越大。而管道屈曲失穩(wěn)后的變形由海床對管道的殘余抗力Hres控制。

[1] HOBBS R E. In- service buckling of heated pipelines[J]. Journal of Transportation Engineering, 1984, 110(2): 175- 189.

[2] 陳驥. 鋼結(jié)構(gòu)穩(wěn)定[M]. 理論與設(shè)計(jì). 北京: 科學(xué)出版社, 2003. (CHEN Ji. Stability of steel structures- theory and design[J]. Beijing: Science Press, 2003. (in Chinese))

[3] 趙天奉. 高溫海底管道溫度應(yīng)力計(jì)算與屈曲模擬研究[D]. 大連理工大學(xué), 2008. (ZHAO Tianfeng. Research on thermal stress and buckling of HT submarine pipelines[D]. Dalian: Dalian University of Technology, 2008. (in Chinese))

[4] LIU R, XIONG H, WU X, et al. Numerical studies on global buckling of subsea pipelines[J]. Ocean Engineering, 2014, 78: 62- 72.

[5] ALVES L, SOUSA J R M, ELLWANGER G B. Transient thermal effects and walking in submarine pipelines[J]. International Journal of Modeling and Simulation for the Petroleum Industry, 2012, 6(1):37- 44.

[6] WHITE D J, CHEUK C Y. Modelling the soil resistance on seabed pipelines during large cycles of lateral movement[J]. Marine Structures, 2008, 21(1): 59- 79.

[7] VERITAS N. Free spanning pipelines[M]. Det Norske Veritas, 2002.

[8] SYSTèMES D. Abaqus analysis user’s manual[M]. ABAQUS Inc., Dassault Systèmes, France, 2007.

[9] RANDOLPH M F, WHITE D J, YAN Y. Modelling the axial soil resistance on deep- water pipelines[J]. Géotechnique, 2012, 62(9): 837- 846.

[10] RANDOLPH M, GOURVENEC M R S. Offshore geotechnical engineering[M]. CRC Press, 2011.

Numerical simulation for the dynamic process of pipeline buckling

WANG Lizhong, WANG Kuanjun, SHI Ruowei

(College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China)

Subsea pipelines are used for transporting high temperature and high pressure oil and gas, which may lead to global buckling of the pipeline. In the process of thermal buckling, the snap- through of the pipeline always exists, which is regarded as a dynamic process. The velocities of the lateral and axial in the dynamic process have great effect on the evaluation of parameters in pipeline- soil interaction analysis. But the study of thermal buckling dynamic process is rarely seen. In this paper, the dynamic process of pipeline thermal buckling is simulated by ABAQUS, and a reasonable evaluation of damping value and heating rate is provided. The variation of the initial geometric imperfection and seabed parameters are also taken into consideration to analyse the dynamic process of pipeline thermal buckling.

subsea pipeline; thermal buckling dynamic process; damping value; heating rate; initial geometric imperfection; seabed parameters

TE832

A

10.16483/j.issn.1005- 9865.2015.05.010

1005- 9865(2015)05- 073- 08

2014- 07- 18

國家杰出青年科學(xué)基金資助項(xiàng)目(51325901)；國家自然科學(xué)基金面上資助項(xiàng)目(51279176)

王立忠(1969- )，男，教授,主要研究方向?yàn)楹Ｑ髱r土工程。E- mail: wlzzju@163.com