一種快速非線性海浪數值仿真方法

王　嵐，周霖儀，聶衛東

（1.中國船舶重工集團公司 第705研究所，陜西 西安，710075；2.中國艦船研究院，北京，100192）

一種快速非線性海浪數值仿真方法

王嵐1，周霖儀2，聶衛東1

（1.中國船舶重工集團公司 第705研究所，陜西 西安，710075；2.中國艦船研究院，北京，100192）

在海面微波散射等海洋軍事研究領域，關于非線性海浪的數值仿真問題日益受到重視。在借鑒已有研究成果的基礎上，提出了一種快速的非線性海浪數值仿真方法，其基本思想是依據非線性海浪的統計特性對線性仿真數據進行非線性修正，從而得到所需結果。通過采用基于JONSWAP譜的線性濾波并依據B分布特性進行非線性修正的方法對深水無破碎二維非線性海浪進行數值仿真。分析表明，該方法能夠快速而有效地模擬非線性海浪，所得仿真數據不僅體現了非線性海浪波面位移的偏態分布特性，而且在波動能量分布上，仿真結果與JONSWAP譜所代表的海浪記錄接近。

非線性海浪；JONSWAP譜；B分布；非線性修正

0　引言

迄今所提出的種種海浪線性模型都是將海浪描述為線性小振幅簡單波動的疊加，并假定作為組成波的這些簡單波動是隨機而相互獨立的，

疊加結果為具有各態歷經性的平穩正態過程，以此過程描述海浪即構成所謂線性海浪模型［1-4］。雖然這種模型具有理論推證完備和應用方便等優點，但它對海浪的描述與實際海浪現象是有偏差的，實際的海浪振幅相對于波長并不小，波面位移的概率分布是偏離正態的，而這種偏離反映了非線性的存在，可粗略地理解為這種非線性產生于波-波間的非線性相互作用，這種作用導致波-波間的能量轉移或產生新的波動［5］。非線性海浪的理論研究包括相互聯系的2個方面，一是從物理機制的角度研究波-波間的非線性相互作用；二是研究這種作用所產生的一些偏離正態的海浪統計特征，如偏度和峰度等。波-波間相互作用物理機制的研究在理論和應用上都很重要，但將這項研究的方法和結果直接用于非線性海浪的數值仿真是困難的。因此，一種可行的方法是根據海浪的非正態分布特性直接對線性仿真的結果進行修正，從而有效地進行非線性海浪的數值仿真。劉新安提出了一種非線性修正方法［6］，其依據為非線性海浪的A型Gram-Charlier級數形式分布［7］；Azed Jean-Pierre在其博士論文中，依據非線性海浪的B分布采用Monte Carlo法進行非線性海浪數值仿真［8］，研究了其在海面探測微波散射方面的應用。近年來，非線性海浪數值仿真方面的研究不算活躍，但仍有一些物理或視覺仿真的新方法不斷涌現，在一些綜述性的文獻中有所論及［9-10］。

文中按照上述思想探討了深水無破碎2D非線性隨機海浪的數值仿真，給出了一種基于JONSWAP譜進行線性濾波和依據B分布進行非線性修正的仿真方法，通過對仿真結果的分析，表明此方法具有快速而有效的優點，對某些工程實際問題具有應用參考。

2　海浪波面位移的B分布

實際海浪波面位移的統計分布是非正態的，這已被大量海上和實驗室的觀測結果所證實。雖然在一般情況下，以線性模型或正態過程為近似對許多實際問題的研究可以取得良好的結果，但隨著海洋科技的發展，特別是海洋遙感和海洋軍事技術的發展，正態過程的近似已經不能適應需求，因此海浪特征量非正態分布的研究日益受到重視。M.A.Srokosz對一水庫中測得的風浪試驗數據進行分析［11］，發現波面位移分布與隨機變量的Pearson分布族中的I型符合得很好［4］，其概率密度函數（probability density function，PDF）與M.S.Longuet-Higgins［12］和M.Aziz Tayfun［13］推導的2種形式的非正態PDF相比較，具有形式簡單且不會出現無意義的局部負值情況的優點，因此應用前景較好。Srokosz推導的PDF通過變量代換可化為更為熟悉的B分布形式。下面不采用Srokosz的推導步驟，而以另一種更為簡便的方法加以推導。

判斷Pearson分布類型的參數為

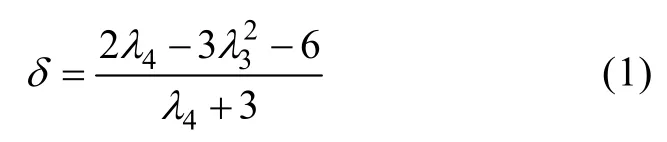
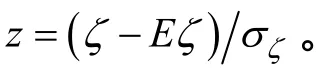
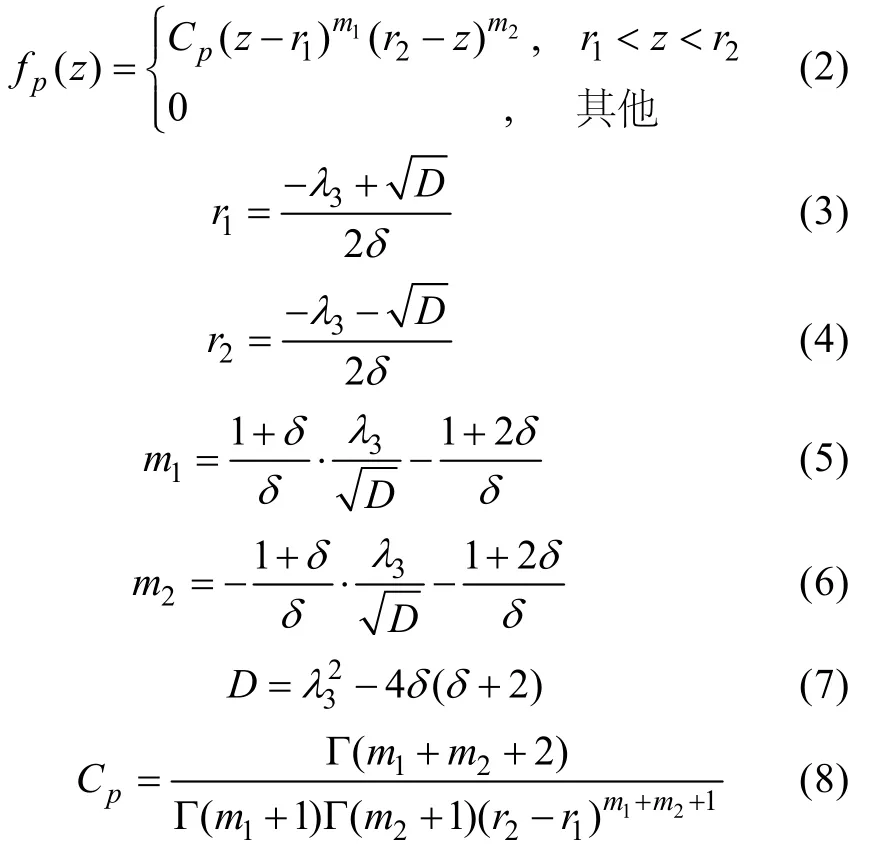
其中，Γ函數由下式確定

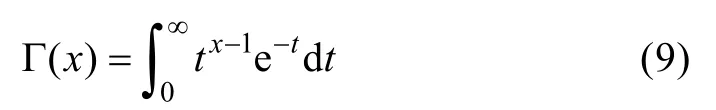
對式（2）作變量代換x=（z-r1）（r2-r1），則得到標準的B分布形式

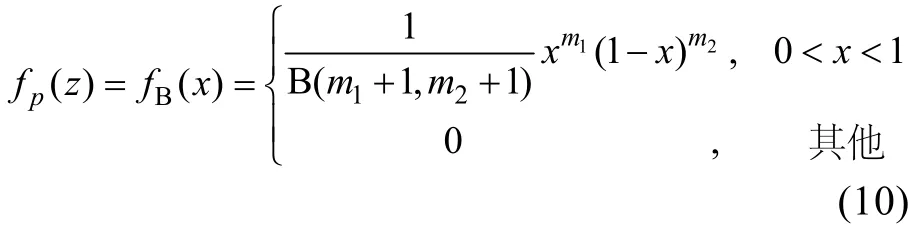
其中，B函數由下式確定

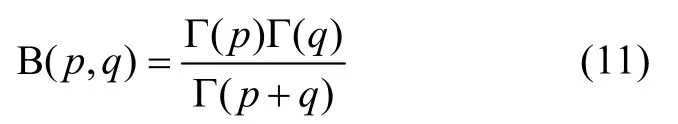
與式（10）對應的標準B分布形式的累積分布函數（cumulative distribution function，CDF）為

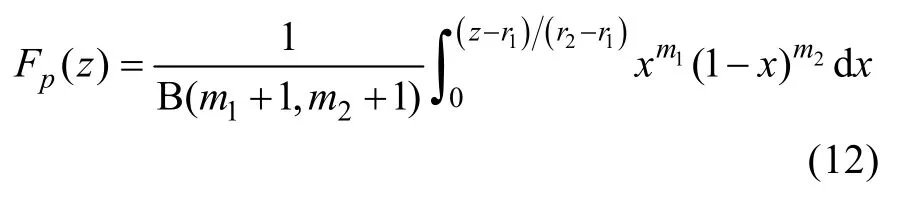
式（12）即為非線性海浪數值仿真時對線性（正態）海浪仿真結果進行修正的計算式。

3　線性（正態）隨機海浪數值仿真的非線性修正

設線性隨機海浪的波面位移為η，將其進行標準化處理，即w=（η-Eη）ση。根據線性海浪理論，w遵從標準正態分布，其PDF為

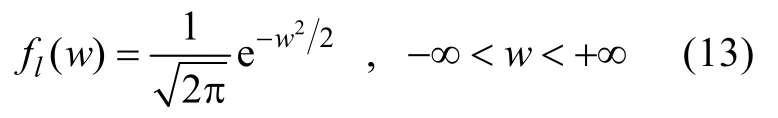
對應的CDF為

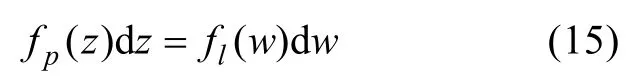
依據文獻［6］的論述，現假定標準化非線性海浪波面位移z與w存在某一函數關系：z=g（w）。根據波數守恒定律，對于不破碎波浪，g（w）為單調上升函數，則由概率論有

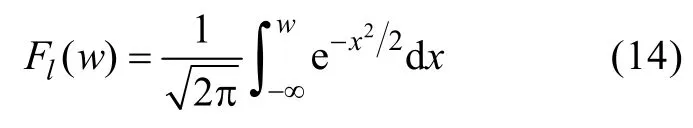
對式（15）積分，并注意積分限，得

就可以進行線性海浪的非線性修正了。由線性海浪的Longuet-Higgins模型［2］易證，2D海浪波面位移為一零均值的平穩正態隨機過程，通過數值仿真解算出線性海浪瞬時固定點標準化波面位移序列w（tn），然后利用式（16）反推非線性海浪瞬時固定點標準化波面位移序列z（tn），從實測數據中得到具有一定偏度的海浪波面位移的均值Eζ和方差σζ，由標準化運算的逆運算得到一段時間內固定點非線性海浪波面位移的數值仿真結果。

關于線性海浪的數值仿真，文獻［14］中有較為詳細的論述。這里采用線性濾波法進行計算，線性濾波法的最大優點在于計算脈沖響應函數和該函數與白噪聲的卷積時可以采用快速（逆）傅里葉變換算法，從而極大提高計算速度。因為JONSWAP譜的數據基礎較為充分，適用面較廣（甚至在颶風條件下仍適用），且考慮了風區參數，所以選取JONSWAP譜作為成形濾波器。值得注意的是JONSWAP譜表達式中峰頻前后有一參數不同，因此在離散化處理時必須先分兩部分進行，而后再合成為一個整體作傅里葉變換。線性濾波法的理論計算式為

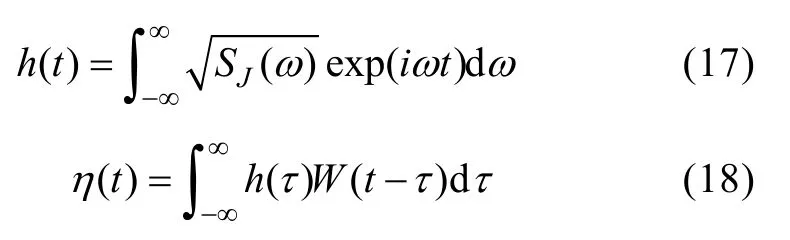
其中：SJ（ω）為JONSWAP譜；ω為波動的圓頻率；W（t）為白噪聲，在實際計算時用程序產生的一系列獨立的標準正態分布隨機變數作為離散的白噪聲序列來逼近理想白噪聲。

在MATLAB環境下計算6 000個點（相當于約100 min的波面位移記錄）約需1 s，與其他方法比較起來速度非常快。

4　非線性隨機海浪數值仿真結果分析

數值仿真計算前選取JONSWAP譜中的海況參數（風速、風區、峰升因子等），首先得到的是線性結果，對線性結果進行非線性修正時由于缺乏相應海況下的實際觀測數據，文中采取了一種簡便且不影響結論的折中方法：在海浪弱非線性的理論前提下，選取一定的波面位移分布偏度和峰度，由線性仿真結果進行修正得到的標準化非線性海浪波面位移序列估計頻譜，將JONSWAP譜峰值除以此譜峰值得到一個功率（能量）比例系數，而后將標準化非線性海浪波面位移序列乘以此比例系數的平方值，這樣便得到了所要的非線性波面位移仿真結果，這樣處理的前提是非線性修正的波面位移必須與JONSWAP譜所代表的海浪記錄具有相同的波動能量。

在線性濾波法計算中隨機白噪聲序列體現了海浪的隨機性，現以任意一次仿真結果來進行分析：選取的風速u=19 m/s ，風區x=50 000 m，峰度因子取平均值γ=3.3，圖1顯示了仿真得到的2D線性隨機海浪波高時間序列和局部放大圖，圖2和圖3分別為線性和非線性仿真結果估計譜S（ω）（稱為實現譜）與JONSWAP譜的對比，圖4為非線性修正后的海浪波高時間序列和局部放大圖。

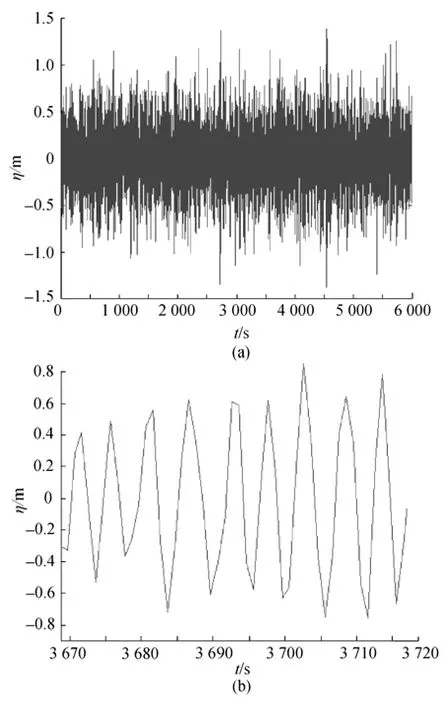
圖1　線性濾波仿真的2D波面位移序列及其局部放大Fig.1　Two-dimensional elevation of wave surface obtained by linear filtering and the enlarged partial view

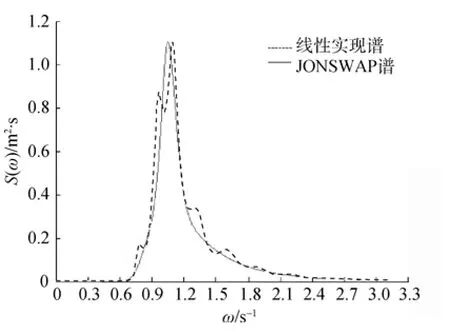
圖2　線性實現譜與靶譜的對比Fig.2　Comparison between linear simulation spectrum and target spectrum

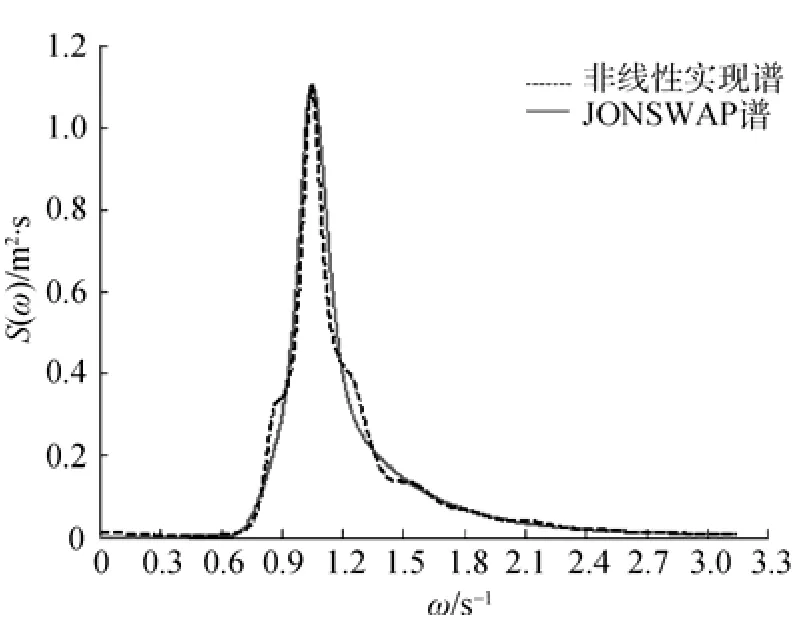
圖3　非線性實現譜與靶譜的對比Fig.3　Comparison between nonlinear simulation spectrum and target spectrum

圖4　非線性修正后得到的2D波面位移序列及其局部放大Fig.4　Two-dimensional elevation of wave surface ob tained by nonlinear correction and the enlarged partial view

線性仿真結果反映了線性隨機海浪外觀上和統計上的特征，即波面位移表現為上下對稱，其均值為2.2×10-5m，接近零，對于線性海浪，可以預見波面位移的偏度和峰度應分別為0和3，這2個參數線性仿真結果分別為0.007 1和2.900 5，接近理論值。非線性修正的輸入偏度為0.55，峰度仍為3，輸出為0.558 5和3.033 1，相當接近輸入值，波面位移表現為波峰部分陡峭而高，波谷部分平緩而淺，具有明顯的偏態分布特征。線性和非線性仿真的實現譜都是標準的傅里葉譜，前者與JONSWAP譜有一定的偏差，并且每次仿真出現的偏差（如峰頻偏移、多譜峰、高頻部分振蕩等）均不同，這反映了隨機白噪聲序列的影響，因為對理想白噪聲的逼近本身就帶來隨機的偏差，值得注意的是非線性實現譜與JONSWAP譜的吻合程度好于線性實現譜，這并非偶然的一次結果，多次重復仿真都表現出這一特征，一種可能的解釋是：在線性隨機海浪理論框架內提出的JONSWAP譜是半理論、半經驗的，雖然不是嚴格的傅里葉譜，但也是通過線性的統計方法擬合得到的，作為其數據來源的實際海浪觀測記錄本身就具有非線性（在統計上主要指偏態分布）的因素。因為非線性數值仿真的結果比線性仿真結果更為接近實際海浪，所以非線性實現譜也應更為接近JONSWAP譜。

5　結束語

非線性隨機海浪數值仿真的應用正日益廣泛，但其中理論上和技術上還有許多沒有克服的困難。文中以一種簡便的方法對非線性的深水二維無破碎風浪進行了數值仿真，分析表明，數值仿真結果在統計意義上較為接近實際狀況，非線性實現譜與JONSWAP譜吻合較好，也表明仿真結果在波動能量分布上與JONSWAP譜所代表的海浪記錄接近，達到了預期的效果。同時，仿真計算簡便快速，可為一些工程應用提供參考。

［1］Pierson，Willard J.A Unified Mathematical Theory for the Analysis，Propagation and Refraction of Storm Generated Ocean Surface Waves［R］.New York：New York University，1952.

［2］Higgins L M S.The Statistical Analysis of a Random Moving Surface［J］.Mathematical and Physical Sciences，1957，249（966）：321-387.

［3］Blair K.Wind Waves［M］.New Jersey：Prentice-Hall Inc.，1965.

［4］Ma T，Yang C Y，Hsiao G C.Optimal Design for Wave Spectrum Estimates［J］.Journal of Geophysical Research，1975，80（Oceans）：1937-1947.

［5］文圣常，余宙文．海浪理論與計算原理［M］．北京：科學出版社，1984：141-142．

［6］劉新安，黃培基．用波面高度分布的非正態特性反演非線性隨機海浪［J］．海洋學報，1994，16（3）：21-30．

［7］Aroian L L.Pearson System of Probability Functions［M］// Van Nostrand′s Scientific Encyclopedia.New York：D.Van Nostrand Company，Inc，1974.

［8］Pierre A J.A Review and Stochastic Simulations of the Nonlinear Properties of Ocean Waves：Applications for Remote Sensing［D］.New York：The City University of New York，2003.

［9］鄒建武，祝明波，董巍．海浪建模方法綜述［J］．艦船電子工程，2010，30（11）：10-14．

Zou Jian-wu，Zhu Ming-bo，Dong Wei.An Overview of Ocean Wave Modeling［J］.Ship Electronic Engineering，2010，30（11）：10-14.

［10］方貴盛，潘志庚．水虛擬仿真技術研究進展［J］．系統仿真學報，2013，25（9）：1981-1989.

Fang Gui-sheng，Pan Zhi-geng.Overview of Modeling Technologies on Water Simulation［J］.Journal of System Simulation，2013，25（9）：1981-1989.

［11］Srokosz，M A.A New Statistical Distribution for the Surface Elevation of Weakly Nonlinear Water Waves［J］.Journal of Physical Oceanography，1998，28（1）：149-155.

［12］Higgins L，M S.The Effect of Nonlinearities on Statistical Distributions in the Theory of Sea Waves［J］.Journal of Fluid Mechanics，1963，17（3）：459-480.

［13］MA T.Narrow-band Nonlinear Sea Waves［J］.Journal of Geophysical Research Oceans，1980，85（C3）：1548-1552.

［14］徐德倫，于定勇.隨機海浪理論［M］．北京：高等教育出版社，2001．

（責任編輯：許妍）

A Fast Simulation Method for Nonlinear Ocean Wave

WANG Lan1，ZHOU Lin-yi2，NIE Wei-dong1
（1.The 705 Research Institute，China Shipbuilding Industry Corporation，Xi′an 710075，China；2.China Ship Research and Development Academy，Beijing 100192，China）

Great emphases have been put on simulation of nonlinear ocean wave in some navy projects.This paper presents a fast method for simulating nonlinear ocean wave in deep sea.The basic idea of this method is to nonlinearly correct the linear simulation data according to the statistic characteristics of nonlinear ocean wave.First，a white noise is filtered by JONSWAP filter to obtain linear result.Then，the linear result is corrected to nonlinear one based on B-distribution characteristics to simulate the blue water two-dimensional unbroken wave.The wave data computed by this method shows the non-normality of real ocean wave.The power spectrum estimated from the nonlinear result is fairly close to JOSWAP spectrum，which indicates that the simulated wave energy distribution accords with the real wave data.

nonlinear ocean waves；JONSWP spectrum；B-distribution；nonlinear correction

P731.22；E993.1

A

1673-1948（2015）04-0316-05

2015-04-01；

2015-06-04

王嵐（1971-），女，高級工程師，研究方向為魚雷總體設計技術、控制技術等.