非自治二階哈密頓系統(tǒng)周期解的存在性

石璐, 安天慶

(河海大學(xué)理學(xué)院,江蘇南京210098)

非自治二階哈密頓系統(tǒng)周期解的存在性

石璐, 安天慶*

(河海大學(xué)理學(xué)院,江蘇南京210098)

用最小作用原理和臨界點(diǎn)理論研究了一類非自治二階哈密頓系統(tǒng)周期解的存在性問題。首先假設(shè)F(t,x)=F1(t,x)+F2(t,x)滿足假設(shè)(A),再使F1滿足次凸條件,并且在[0,T]上的積分趨于無窮,運(yùn)用最小作用原理,得到一個(gè)解的新的存在性結(jié)果。另外,將F1在[0,T]上的積分趨于無窮這一條件減弱為F1在[0,T]的一個(gè)正測度子集E上的積分趨于無窮,運(yùn)用最小作用原理,也能得到同樣的結(jié)果。

次凸位勢;周期解;臨界點(diǎn);最小作用原理

考慮非自治二階哈密頓系統(tǒng)

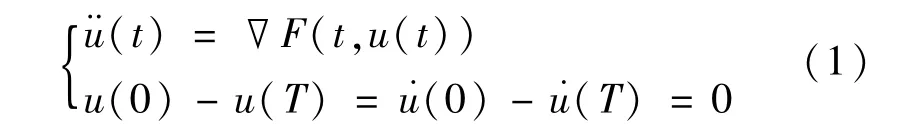
周期解的存在性問題。其中T＞0,且F:[0,T]× RN→R滿足下述假設(shè):(A)對每個(gè)x∈RN,F(t,x)關(guān)于t可測,對a.e.t∈[0,T],F(t,x)關(guān)于x連續(xù)可微,且存在a∈C[R+,R+],b∈L1([0,T];R+),使得

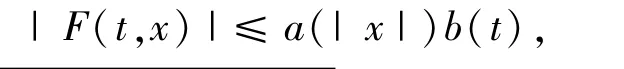
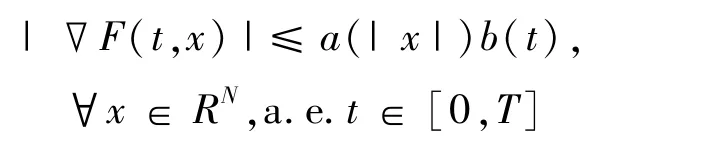
很多學(xué)者已經(jīng)用最小作用原理證明了問題(1)至少有一個(gè)解,且為φ在上的最小值。文中受到文獻(xiàn)[1-4]中結(jié)果與文獻(xiàn)[5-7]中條件的激發(fā),考慮了問題(1)中的次凸問題,同樣通過運(yùn)用最小作用原理,得到問題(1)的解的新結(jié)果。文中假設(shè)F(t,x)=F1(t,x)+F2(t,x)滿足假設(shè)(A)。

1 主要結(jié)果

定理1 假設(shè)F1,F2滿足假設(shè)(A),且

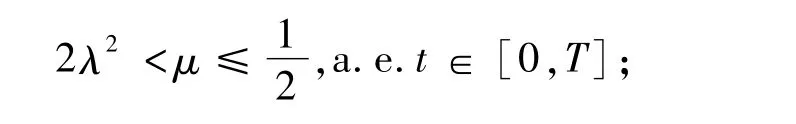
(2)?r∈L1(0,T;R+),α∈[0,2),且

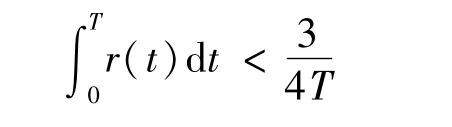
使得

注[2]若對于λ,μ＞0,x,y∈RN,有

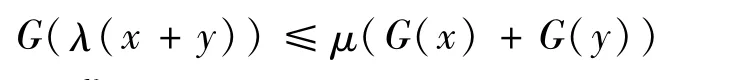
稱函數(shù)F:RN→R為(λ,μ)次凸。

定理2 假設(shè)F1,F2滿足假設(shè)(A),且

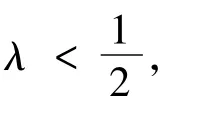
(2)?r∈L1(0,T;R+),α∈[0,2),且

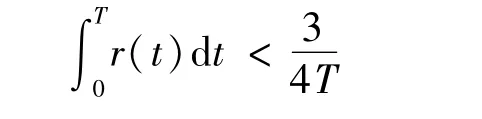
使得

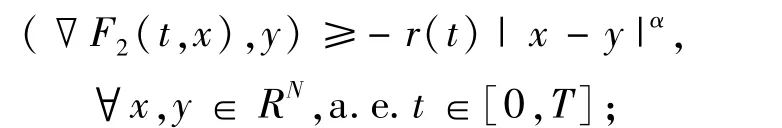
(3)?E?[0,T],且meas(E)＞0,使得

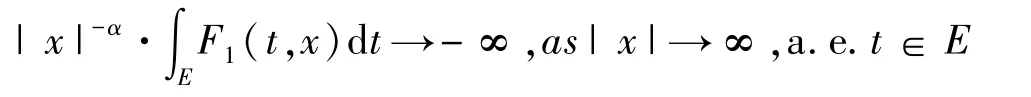
并且?γ∈L1(0,T),使得

則問題(1)至少有一個(gè)解,且為φ在H1T(Ω)上的最小值。

2 定理的證明

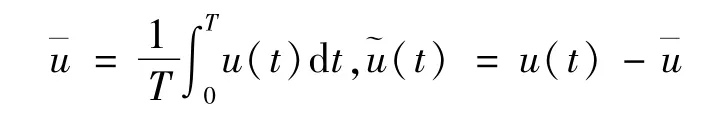
從而有Sobolev不等式和Wirtinger不等式:

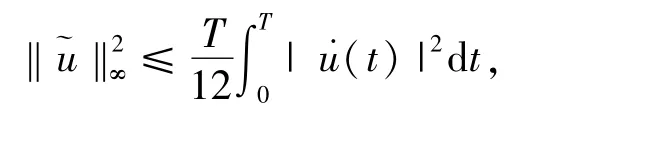
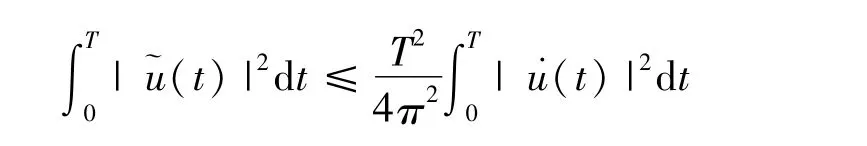
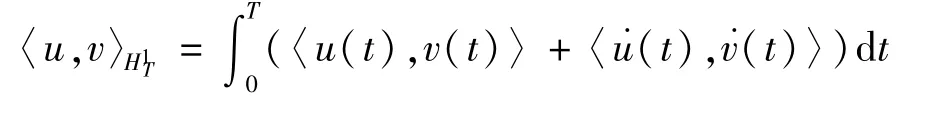
則對應(yīng)的范數(shù)為

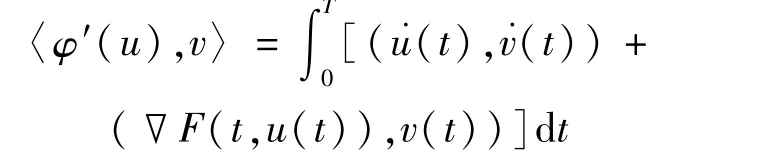
易知問題(1)的解即為φ的臨界點(diǎn)。

由文獻(xiàn)[1]可知,該泛函是下半弱連續(xù)的,因?yàn)閺?qiáng)制的下半弱連續(xù)泛函必有最小值點(diǎn),所以證明定理1和定理2時(shí),只考慮泛函的強(qiáng)制性。

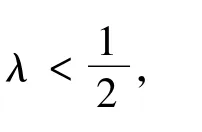
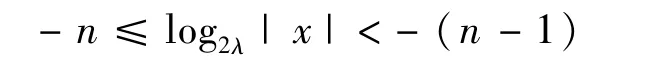
則由(2λ)-(n-1)＜|x|≤(2λ)-n,有

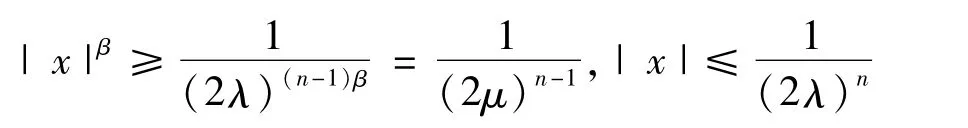
所以由條件(1)和假設(shè)(A),對于a.e.t∈[0,T]和所有的|x|≥1,有

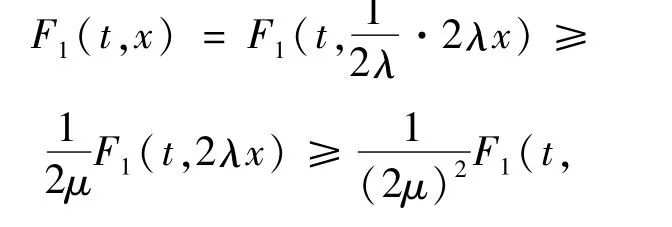
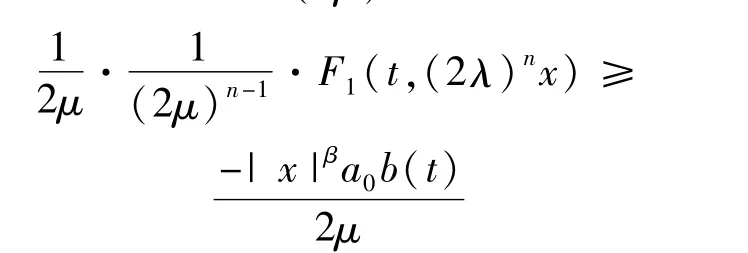
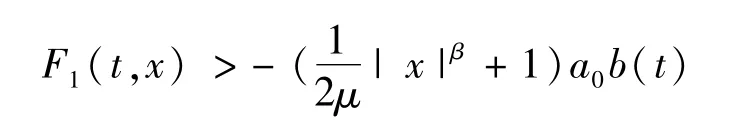
其中β＜2。

又F1(t,·)是(λ,μ)次凸,則

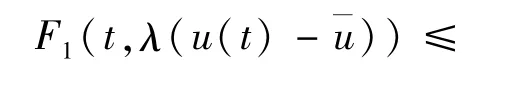
其中a0=max0≤s≤la(s)。

進(jìn)一步,知道對于a.e.t∈[0,T]和所有的x∈RN,有

即

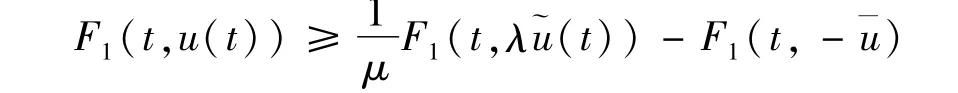
由條件(1)和Sobolev不等式,有

其中c1,c2均為正常數(shù)。

由條件(2),知道

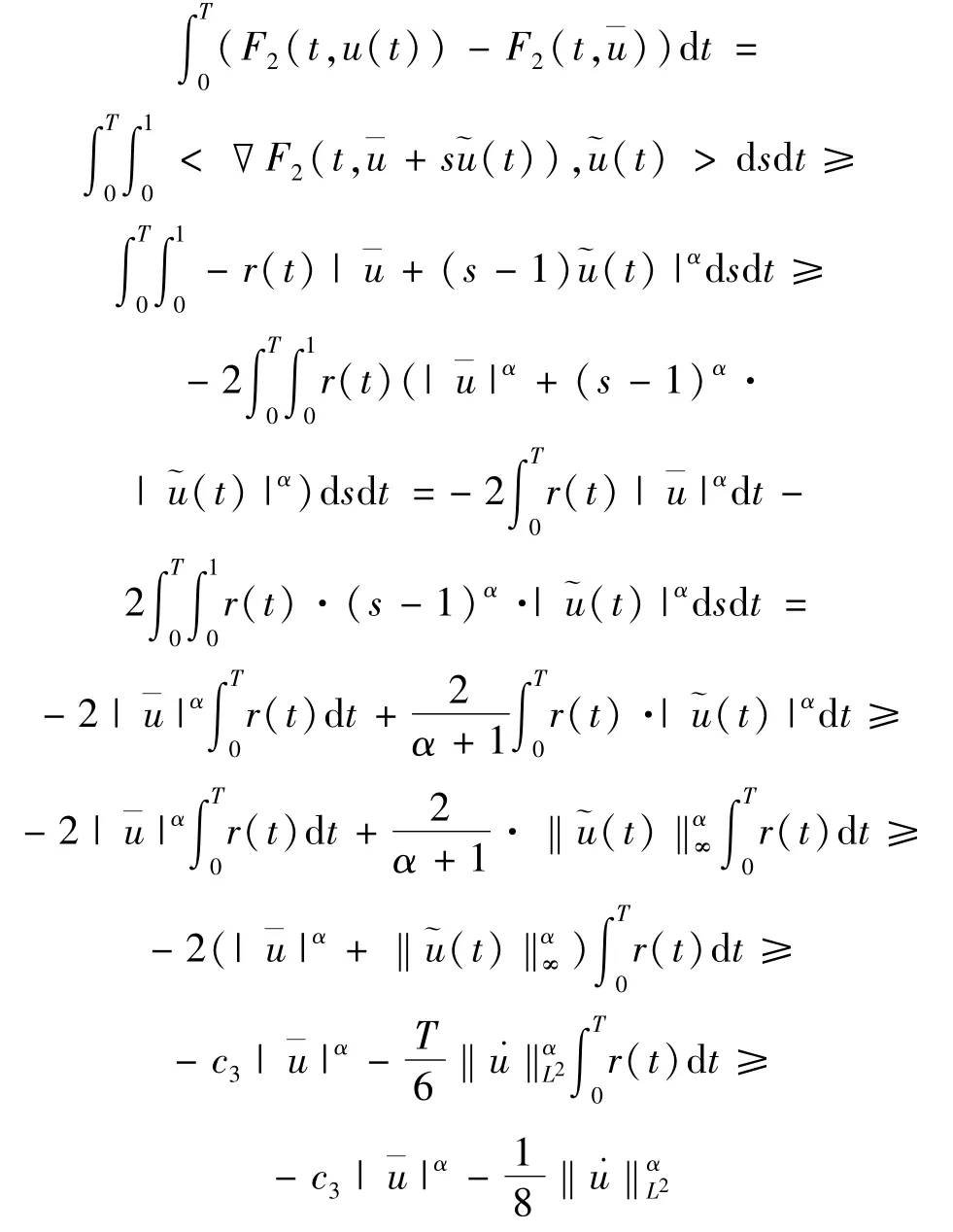
所以

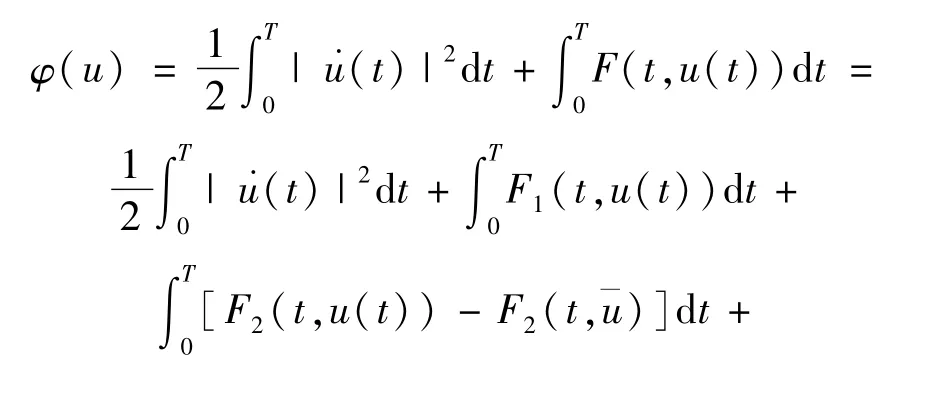
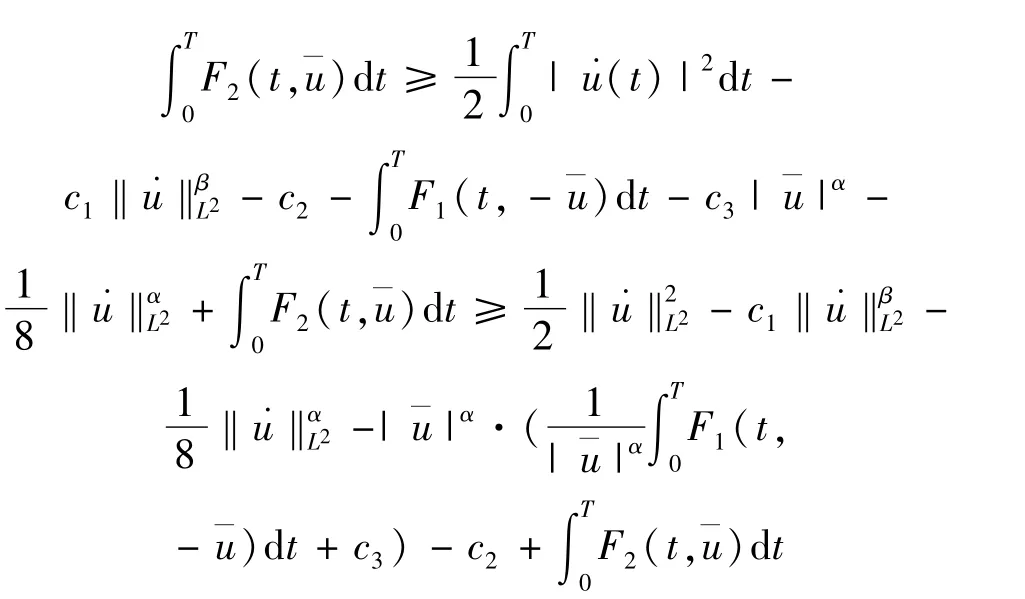
由于

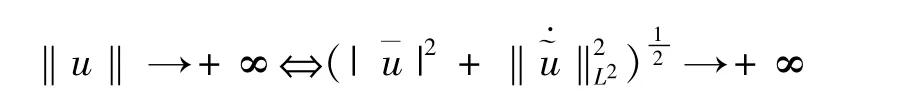
則由條件(3),β＜2,α∈[0,2),知道

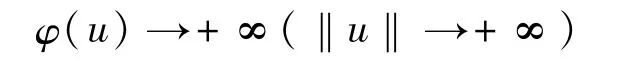
證畢。

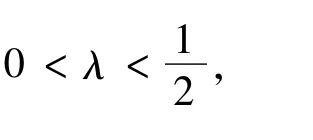
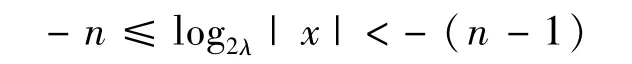
則由(2λ)-(n-1)＜|x|≤(2λ)-n,有

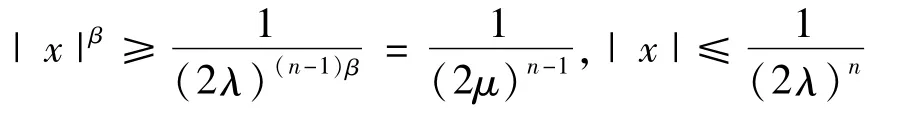
所以由條件(1)和假設(shè)(A),對于a.e.t∈[0,T]和所有的|x|≥1,有

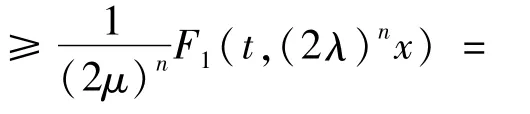
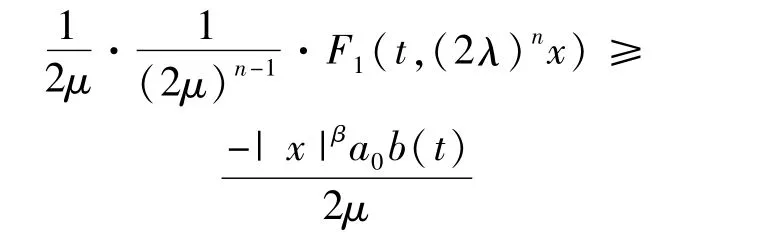
其中a0=max0≤s≤la(s)。

進(jìn)一步,知道對于a.e.t∈[0,T]和所有的x∈RN,有

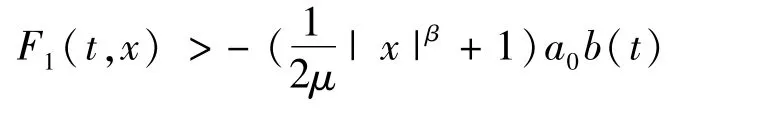
其中β＜2。

又F1(t,·)是(λ,μ)次凸,則

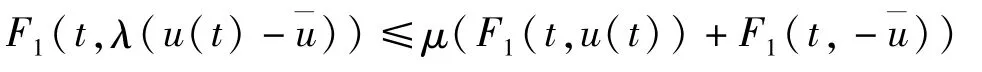
即

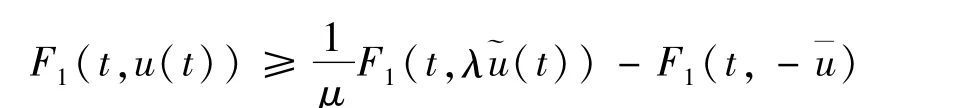
由條件(1)和Sobolev不等式,有

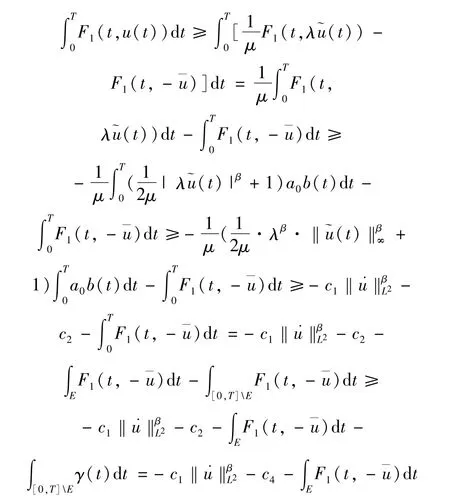
其中c1,c2,c4均為正常數(shù)。

由條件(2),知道

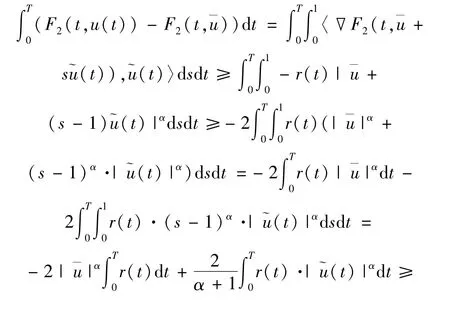
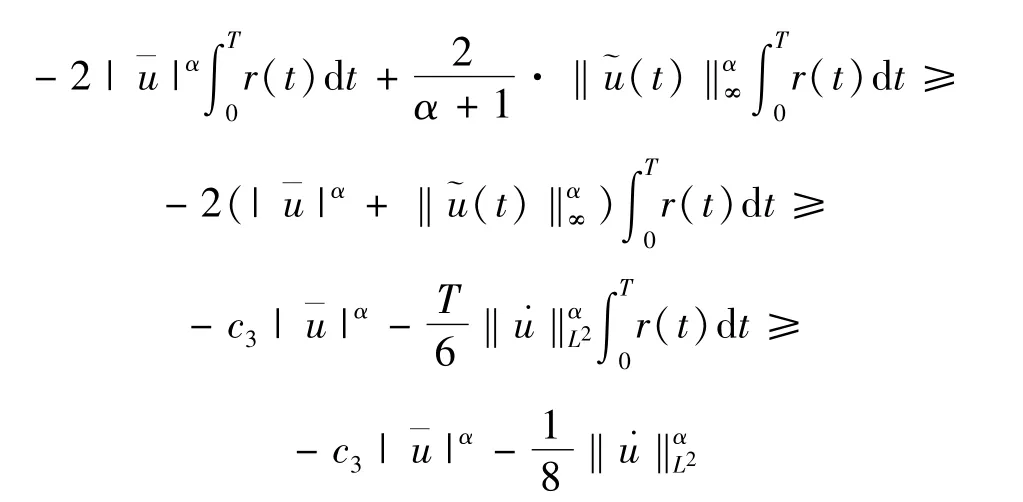
從而

由于

則由條件(3),β＜2,α∈[0,2),知道

證畢。

[1]Mawhin J,Willem M.Critical Points Theory and Hamiltonian Systems[M].New York:Springer-Verlag,1989.

[2]WU Xingping,TANG Chunlei.Periodic solutions of a class of nonautonomous second order systems[J].JMath Anal Appl,1999, 236:227-235.

[3]孟鳳娟.一類二階哈密頓系統(tǒng)周期解的存在性[J].河南科學(xué),2010,28(1):21-24.

MENG Fengjuan.Existence of periodic solutions for a class of second order Hamiltonian systems[J].Henan Science,2010,28 (1):21-24.(in Chinese)

[4]ZHAO Fukun,WU Xian.Periodic solutions of a class of nonautonomous second order systems[J].JMath Anal Appl,2004,296: 422-434.

[5]Nurbek Aizmahin,AN Tianqing.The existence of periodic solutions of nonautonomous second order Hamiltonian systems[J]. Nonlinear Analysis,2011,74:4862-4867.

[6]MA Jian,TANG Chunlei.Periodic solutions for some nonautonomous second order systems[J].JMath Anal Appl,2002,275:482-494.

[7]TANG Chunlei.Periodic solution of nonautonomous second order systems[J].JMath Anal Appl,1996,202:465-469.

(責(zé)任編輯:楊 勇)

Existence of Periodic Solutions for Nonautonom ous Second O rder Ham iltonian System

SHILu, AN Tianqing*
(College of Science,Hohai University,Nanjing 210098,China)

By using the least action principle and the critical point theory,this paper studies the existence of the periodic solutions for a class of non-autonomous second-order Hamiltonian systems.First,assuming that F(t,x)= F1(t,x)+F2(t,x)satisfies hypothesis(A),then F1meets the subconvex condition,and the integration tends to infinity in[0,T],we can obtain a new existence theorem by using the leastaction principle.Moreover,weweaken the condition that the integration of F1tends to infinity in[0,T]to the case that the integration of F1tends to infinity in a positive measure subset E of[0,T],we can get the same result by using the least action principle.

subconvex potential,periodic solutions,critical points,the least action principle

O 177

A

1671-7147(2015)01-0117-04

2014-09-12;

2014-09-25。

河海大學(xué)中央高校業(yè)務(wù)費(fèi)項(xiàng)目(B12020128)。

石璐(1990—),女,江蘇淮安人,基礎(chǔ)數(shù)學(xué)專業(yè)碩士研究生。

*通信作者:安天慶(1963—),男,甘肅古浪人,教授,博士生導(dǎo)師。主要從事非線性泛函分析等研究。

Email:antq@hhu.edu.cn