基于可靠度理論的巖質邊坡經濟風險評價

高 策，陳建康，吳震宇，周正軍，王 滔

(四川大學水利水電學院，四川 成都 610065)

0 引言

巖質邊坡穩定與邊坡破壞模式、所處位置、破壞方量密切相關。在邊坡實際開挖中，斷層出露、人工擾動等因素對邊坡穩定的影響較大。目前，評價邊坡穩定主要有2種方法，一種是基于安全系數的評價方法，這種方法雖然有統一的評價標準，但安全系數人為給定，且把不確定荷載、巖土參數等作為確定量考慮，這顯然是不符合實際的;另一種是基于可靠度理論的評價方法，該方法把影響邊坡穩定的各種因素作為隨機變量考慮，以概率論與數理統計為基礎，計算邊坡的可靠度指標和失效概率。如H.S.B.Duzgun等［1］研究了基于可靠度理論的巖質邊坡平面滑動破壞時的設計方法;B.K.Low［2-3］提出了基于Excel的可靠指標計算的新算法;R.Jimenez-Rodriguez等［4］采用不相交的割集模擬巖質邊坡平面滑動的體系可靠度問題;張興、廖國華［5］采用蒙特卡羅方法計算了多滑面邊坡的體系可靠度;譚曉慧等［6］以增量切線剛度法為基礎，推導了基于修正的Aitken加速法的非線性隨機有限元加速迭代公式，并將其應用于邊坡穩定的可靠度分析中;吳震宇等［7］采用Ditlevsen窄界限公式估算了巖質邊坡各失穩模式組成的串聯體系的可靠指標;李典慶等［8］提出了基于n維等效方法的巖質邊坡楔體穩定體系可靠度分析方法。

盡管可靠度理論在巖質邊坡穩定研究中已取得了一些進展，但由于沒有形成以可靠度分析為基礎的規范，缺乏統一的評價標準，且計算出來的可靠度和失效概率無法對邊坡的失穩風險進行直觀的評價。因此，尋找一個可以把風險量化的指標成為風險評價的首要問題。王偉等［9］以經濟作為風險評價指標，基于投資最省原則，確定邊坡可接受的可靠性指標或破壞概率，從而判定邊坡的穩定性;田斌等［10］以經濟風險分析為基礎，對巖質高邊坡加固方案進行分析;曾晟等［11］提出基于可靠度的圓弧滑動邊坡經濟風險分析模型優化方法。本文在此基礎上，以某工程邊坡為例，建立了巖質邊坡風險損失與支護量之間的關系，基于風險損失最小的原則，確定了該巖質邊坡較為合理的支護方案。

1 邊坡支護的經濟風險分析流程

1.1 支護條件下邊坡失效概率的計算

采用非線性有限元計算，通過逐步降低巖土體強度參數尋找潛在的滑移通道，并認為滑移通道上所有單元失效時邊坡即失穩。因此，有幾條滑移通道就有幾種失穩模式。假設有m種失效模式，第n個失效模式下有j個單元，依據Druker-Prager屈服準則構建單元的功能函數，定義第n個失效模式下第i個單元表示為，則功能函數為

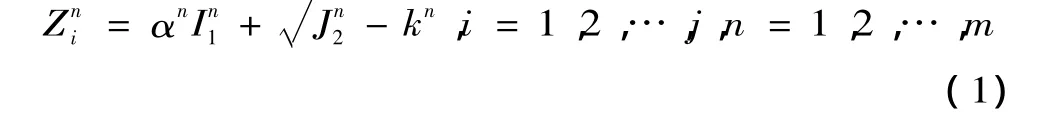
由于式(1)中含有不能顯式表達的應力項，采用不含交叉項的二次多項式構建單元功能函數的響應面方程為

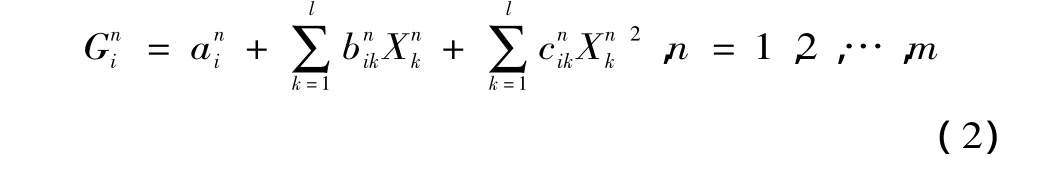
根據有限元計算和回歸分析得出待定參數后，就可以采用蒙特卡洛隨機抽樣法計算單元的失效概率和相關系數。當破壞通道上的所有單元都失效時，認為邊坡破壞失穩。因此，單一模式下失效概率可按并聯體系進行計算，采用PNET法［12］近似計算并聯體系的失效概率。在評價邊坡整體穩定性時，由于存在多種滑移通道，每一條滑移通道失穩，則邊坡整體失穩。因此，在求得各失穩模式的失效概率后，計算各失穩模式間的相關系數，最后按Ditlevsen［13］窄界限公式估算各失穩模式組成的串聯體系的失效概率。

1.2 風險分析流程

在風險分析中，考慮資金的時間價值時通常可從靜態和動態角度考慮。邊坡工程開挖過程通常為人為活動，實施周期較短，為簡化分析流程，可從靜態的角度進行分析。常規的邊坡穩定計算僅從保證邊坡安全的角度出發，難以量化地評價邊坡支護成本及風險損失之間的關系。邊坡風險損失可由邊坡失穩概率Pf和損失c這2個因素組成的函數表示，即

式中，R為邊坡災害活動的風險損失;Pf為邊坡發生災害活動的概率;c為邊坡災害活動產生的損失后果。

用邊坡的經濟指標來評價邊坡的風險，采用費用值來表示邊坡可靠性的影響效應。邊坡開挖的總費用Cs可表示為

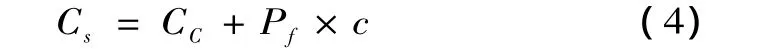
式中，CC為邊坡開挖和加固費用。

按照經濟風險評價的基本理念，對巖質邊坡的失穩風險及其支護效果進行分析和評價:

(1)根據邊坡的實際情況，先利用剛體極限平衡法對邊坡進行穩定計算，判定目標邊坡的穩定性，擬定必要的邊坡穩定處理措施(如削坡、錨固等)。

(2)確定處理措施的控制變量。對削坡選取削坡高度、削坡角度作為控制變量;對錨固措施可將錨固數量、錨索噸位等作為控制變量。

(3)根據具體處理措施確定成本Cc，在相應的處理措施下對邊坡進行可靠度分析，可以得到相應的Pf。根據最危險滑面的位置可以計算出滑體方量，從而間接得出滑動后造成的風險損失數額c。

(4)將Cc，Pf和c代入公式(4)，計算得到不同處理措施下邊坡開挖的總費用Cs，每種處理措施即可算出一個與之對應總成本，由此得到邊坡開挖總費用Cs和不同處理措施控制變量之間的關系曲線。若Cs值始終隨控制變量的變化而增大，則說明邊坡不需要治理或該治理措施效果不佳，不宜采用;若曲線具有極小值的拐點，則該極小值對應的邊坡破壞概率為邊坡可接受的破壞概率值，由此可得到對應的可靠性指標，此時的處理措施可作為邊坡的最優治理措施。巖質邊坡支護效果評價流程見圖1。

2 工程應用

2.1 工程概況

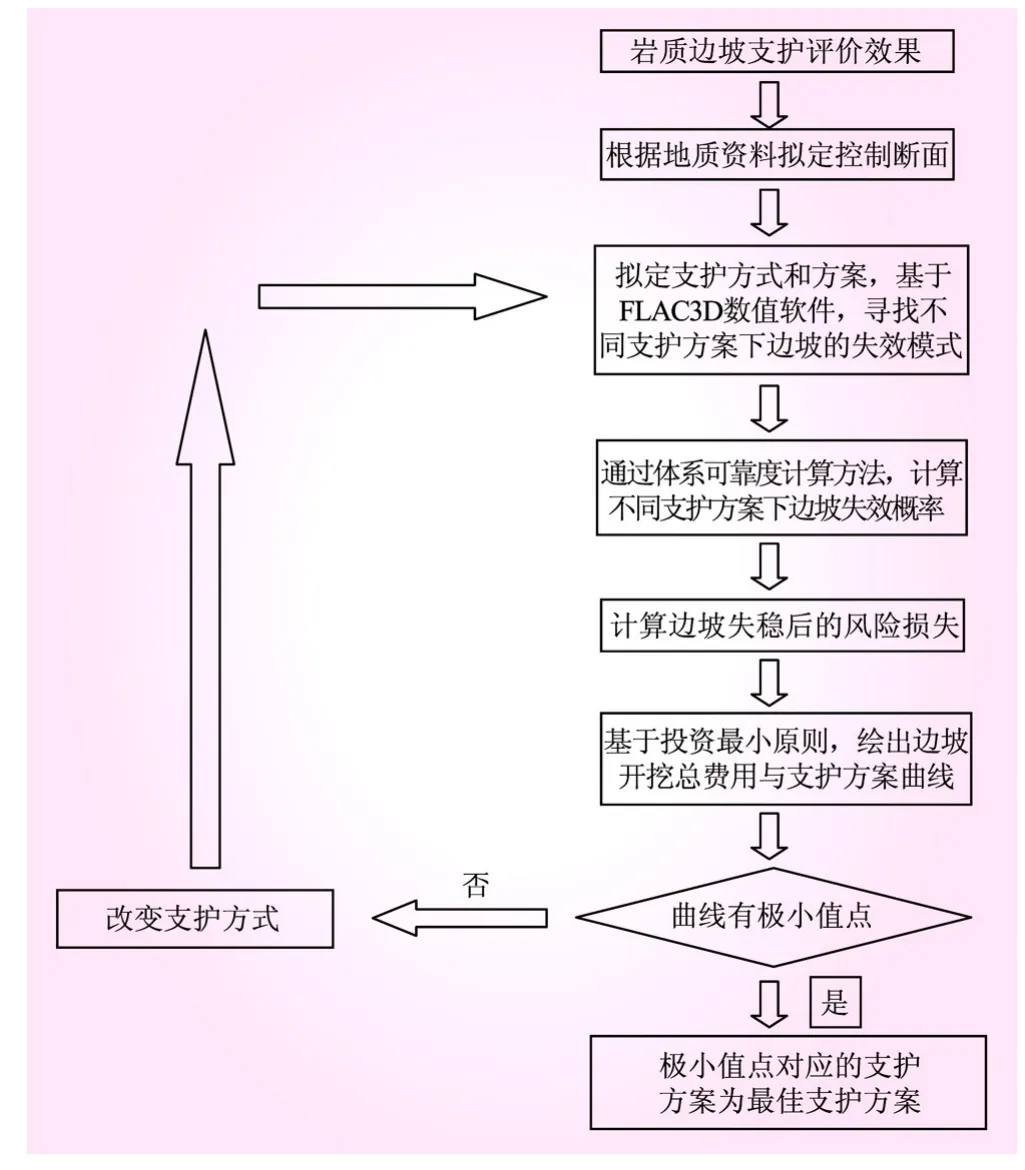
圖1 巖質邊坡支護效果評價流程

某料場位于某壩址下游，距壩址約7 km，沿河長約800 m，分布高程1690～2000 m，地形坡度40°～45°，開采坡比 1∶0.4 ～1∶0.3，部分強卸荷巖體采用1∶0.5，每隔30 m設置1條3 m寬馬道，分10級開挖。料場地層巖性為前震旦系斑狀流紋巖夾少量含絹云母片巖，巖石弱～微風化，巖質致密堅硬。基巖主要發育有4組構造裂隙，L1:N65°E/SE∠80°;L2:N25°～30°E/NW∠70°～75°;L3:EW/S∠80°～85°;L4:N45°～50°W/SW∠50°～60°。料場區域地下水不發育，無需考慮滲流影響。

2.2 邊坡處理措施確定

根據地質資料中邊坡的地質結構、斷層分布情況和構造情況，將斷面P10、P11、P12和P14作為控制斷面［14］。采用 Morgenstern-Price法，對地震工況下終采邊坡進行穩定計算。P10、P11、P12和P14安全系數分別為 0.973、0.985、0.952、0.933和0.991。

料場終采邊坡為B類Ⅲ級邊坡。根據DL/T 5353—2006《水電水利工程邊坡設計規范》，采用邊坡設計安全系數的下限值，即偶然狀況(地震工況)為1.00。計算結果可知，各控制斷面安全系數均不滿足要求，該邊坡需要支護處理。由于該料場邊坡滑移塊體大，采用削坡治理方案不經濟，故最終采用錨索支護進行處理。

2.3 邊坡失穩風險分析

2.3.1 計算模型及參數

基于FLAC3D軟件，采用三維等參元對邊坡地質模型進行網格劃分，裂隙、次級小斷層和擠壓破碎帶采用薄層實體單元模擬。邊坡計算模型共劃分為97698個單元和102718個節點。模型底部施加固端約束，側面施加法向約束。邊坡開挖前后網格劃分見圖2。巖體和結構面的屈服和破壞準則采用Druker-Prager準則。料場邊坡巖體和結構面力學參數見表1。

圖2 料場邊坡網格劃分

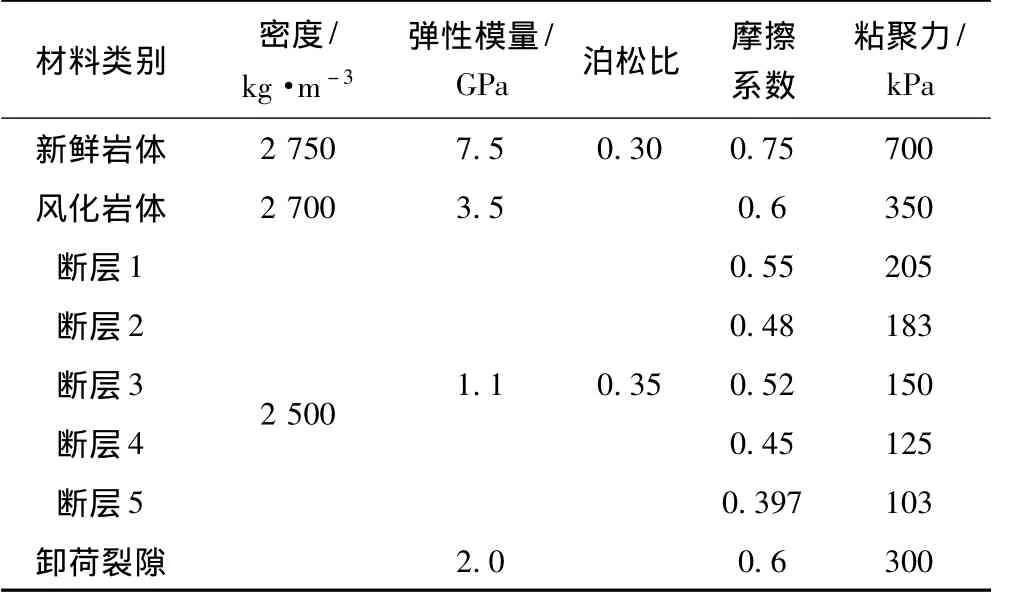
表1 料場邊坡巖體和結構面力學參數

2.3.2 支護方案

錨索由錨索單元模擬，預應力錨索的錨固作用通過在錨索兩端施加等效錨固力考慮，錨索支護按滯后開挖一級施加。采用開挖一級支護一級的方式，擬定了6種支護方案。方案1:無錨索支護;方案2:錨索數量5根，2、4、5、7、8級馬道錨索1根;方案3:錨索數量10根，1～7、9馬道布置1根錨索，8級馬道2根錨索;方案4:錨索數量15根，1、3、6馬道1根錨索，2、4、5、7馬道2根錨索，8級馬道3根錨索;方案5:錨索數量20根，1～4、7、9馬道2根錨索，5、8馬道3根錨索;方案6:錨索數量25根，1、9馬達2根錨索，2～8馬道3根錨索。以上支護方案錨索間隔均為6 m，噸位200 t。

2.3.3 不同支護量下的失穩風險

以巖體及結構面的摩擦系數和粘聚力為隨機變量，考慮地震的超越概率，根據式(1)～(7)計算，得到不同支護量下邊坡開挖失效概率。不同支護量下邊坡失效概率見圖3。從圖3可知，同一開挖步下，隨著錨索的增加，失效概率逐漸降低;相同錨索數量下，隨著邊坡不斷開挖，失效概率逐漸增大。

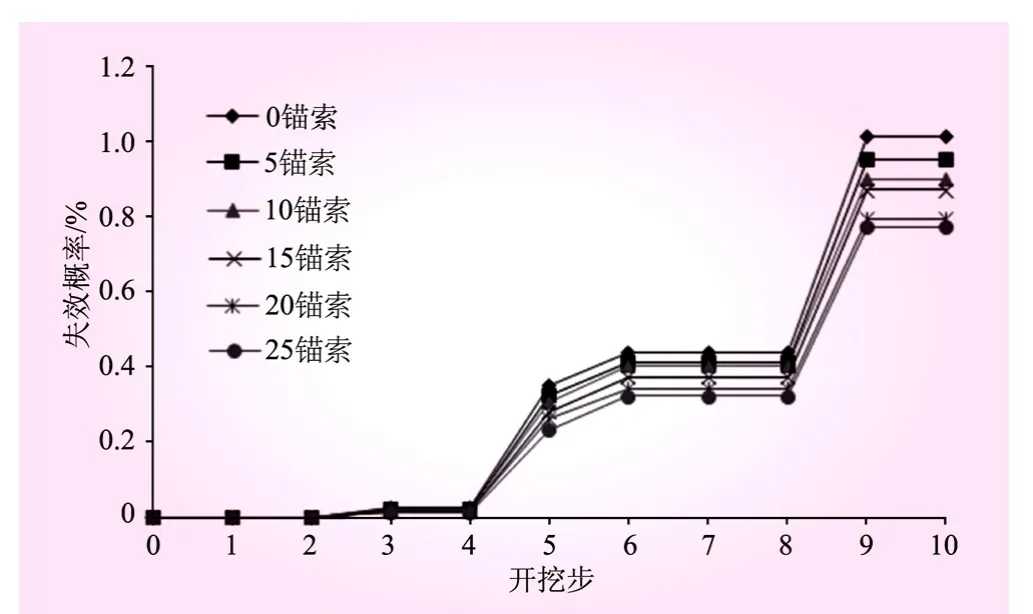
圖3 不同支護量、不同開挖步下邊坡失效概率

3 邊坡支護效果評價

本文計算中，邊坡滑移體滑移后的清除整理費為60元/m3，錨索造價為3.8元/m。根據本文給出的風險模型，得出不同支護量下各級開挖的風險損失(見圖4)。從圖4可知，在不同支護量下，邊坡各級開挖的風險分布與邊坡的失效概率分布類似。

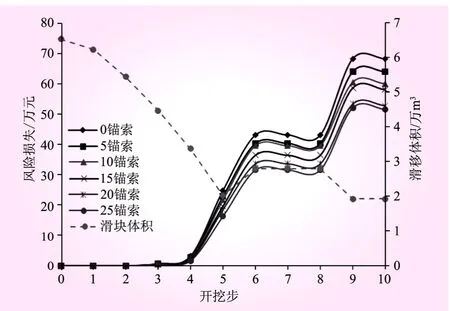
圖4 不同支護量下邊坡開挖風險

在天然邊坡和開挖1～4級中，邊坡的失效塊體的體積較大，其體積隨邊坡的開挖逐漸減小，邊坡的風險值也呈現減小的趨勢，但邊坡的風險值很小接近于0，主要原因為天然邊坡和開挖1～4級中邊坡的失效概率很低。在第5級邊坡開挖中，有緩傾角斷層出露，與陡傾角斷層形成不穩定的滑移塊體，滑移塊體的體積相對較小，其失效概率較大。第6級邊坡開挖中，有緩傾角斷層出露，并與陡傾角斷層構成較危險的滑移通道，其失效塊體的體積與失效概率均比第5級有所提高，風險值較大。第7、8級邊坡開挖中，邊坡沒有新的斷層出露，其風險主要受第6級開挖的滑移通道控制，兩級開挖的風險值基本相同。第9級開挖中，新的緩傾角斷層出現，與陡傾角斷層構成新的較危險的滑移塊體，其體積在整個邊坡開挖過程中最小，但因其失效概率最大，故風險損失值也最大。完建邊坡的風險，主要受第9級開挖后的滑移通道控制，其風險損失值比第9級開挖略有減小。

取完建邊坡作為研究對象，將費用成本值作為經濟指標衡量支護效益。完建邊坡費用總成本與支護量曲線見圖5。從圖5可以看出，隨著支護量的增加，邊坡的失效概率減小，風險損失減小，開挖加固費用增加，兩者之和總成本先減小后增加，在支護量為10處曲線出現最低點，表明支護方案3為較為合理的支護方案。

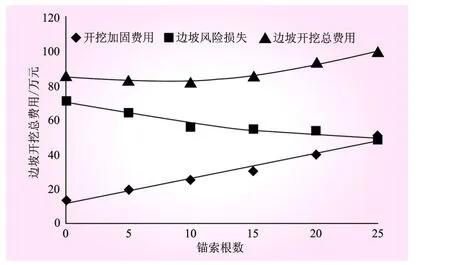
圖5 不同支護量下完建邊坡開挖總費用

4 結論

本文對某工程料場邊坡在不同支護條件下進行可靠度計算，應用經濟風險評價方法對不同支護方案進行評價，得到以下結論:

(1)結合可靠度計算成果，將計算得出的失效概率量化，以失效后造成的經濟損失作為評價指標，得到邊坡風險損失隨支護量增加而降低，支護量越多，邊坡的失效概率越小，即邊坡越安全的結論。與計算得到的失效概率規律相同，證明了該方法的可行性。

(2)完建工況下邊坡支護的總成本隨支護量的增加先減少后增加，出現極小值拐點，說明采用200 t級錨索擬定的支護方案是可行的，找出了邊坡失效風險與經濟損失的平衡點，并最終確定了較為合理的支護方案。

［1］DUZGUN H S B，YACEMEN M S，KORPUZ C A.A methodology for reliability-based design of rock slopes［J］.Rock Mechanics and Rock Engineering，2003，36(2):95-120.

［2］LOW B K.Reliability analysis of rock slopes involving correlated nonnormals［J］.International Journal of Rock Mechanics and Mining Sciences，2007，44(6):922-935.

［3］LOW B K.Efficient probabilistic algorithm illustrated for a rock slope［J］.Rock Mechanics and Rock Engineering，2008，41(5):715 –734.

［4］JIMENEZ-RODRIGUEZ R，SITAR N，CHACON J.System reliability approach to rock slope stability［J］.International Journal of Rock Mechanics and Mining Sciences，2006，43(6):847-859.

［5］張興，廖國華.多滑動面邊坡的破壞概率［J］.巖土工程學報，1990，12(6):55-62.

［6］譚曉慧.多滑面邊坡的可靠性分析［J］.巖石力學與工程學報，2001，20(6):822-825.

［7］吳震宇，陳建康，許唯臨，等.巖質邊坡穩定的體系可靠度分析及工程應用［J］.四川大學學報:工程科學版，2008，40(2):32-37.

［8］李典慶，周創兵，胡冉.基于n維等效方法的巖質邊坡楔體穩定體系可靠度分析［J］.巖石力學與工程學報，2009，28(7):1415-1424.

［9］王偉，楊敏，劉德富.基于經濟風險分析的邊坡穩定性評價［J］.同濟大學學報:自然科學版，2004，32(12):1603-1607.

［10］田斌，張萍，劉德富.巖石高邊坡加固方案決策的經濟風險分析［J］.工程地質學報，2007，15(Sl):502-506.

［11］曾晟，楊仕教，譚凱旋，等.基于可靠度的圓弧滑動邊坡經濟風險分析模型優化方法［J］.南華大學學報:自然科學版，2009，23(4):107-110.

［12］吳世偉.結構可靠度分析［M］.北京:人民交通出版社，1990.

［13］DITLEVSEN O.Narrow reliability bounds for structural system［J］.StrutMech，1979，4(1):117-122.

［14］李鵬，何江達，謝紅強，等.地震作用下巖質邊坡動力響應分析［J］.水力發電，2014，40(2):41-45.