基于仿真分析的橋梁承載能力評估

劉菊玖 劉望平

(廣州市市政工程設計研究院,廣東廣州 510060)

基于仿真分析的橋梁承載能力評估

劉菊玖 劉望平

(廣州市市政工程設計研究院,廣東廣州 510060)

橋梁結構承載能力是舊橋檢測的關鍵指標之一，結合廣州市某立交橋的模態測試結果,對比橋梁結構破損前后低階模態參數的變化,對橋梁的有限元模型參數進行仿真修正,依據經過仿真修正的計算模型對橋梁結構進行承載力檢算和評估。

橋梁結構;承載力;仿真分析;模態試驗

0 引言

橋梁結構的使用效能及耐用年限,主要由設計、施工和所使用材料的質量以及運營狀況而定。設計、施工和材料可能存在某些缺陷,這些缺陷使橋梁結構先天就存在某些薄弱點,橋梁在運營使用中又會受到不可避免的人為損害及各種大自然侵蝕而帶來后天病害。先天缺陷和后天病害的不利影響一旦結合在一起,再遇上荷載和外力的臨界組合,很容易使橋梁結構發生不能預見的損壞。一處或某幾處局部的損壞還可能產生連鎖反應,波及到更多的部位,發展成更大的損壞,以至危及橋梁主體結構的安全。

橋梁結構的檢查,是保證橋梁正常使用、進行維修加固的依據。及時的檢查可以較早地發現橋梁的病害,減小維修工作量；如果病害發現得越晚,維修工作量就越大。檢查不及時或者不充分都會使橋梁病害得不到及時發現而存在安全隱患。因此,橋梁結構檢查的目的在于隨時掌握結構的技術狀況和安全狀況,較早地發現缺損和異常情況,及時提出和采取必要的養護措施,保證行車和行人的安全,延長其使用壽命。

目前舊橋的承載能力鑒定的依據是《公路橋梁承載能力檢測評定規程》(JTG/T J21-2011)［1］,而且在實際中很多情況下依據荷載試驗來進行橋梁承載能力檢算。具體方式基本為：將通過荷載試驗獲得的撓度校驗系數η按照文獻［1］提供的撓度校驗系數η與檢算系數Z2的關系確定橋梁的檢算系數Z2，然后對橋梁進行檢算。然而,在某些情況下,很難進行荷載試驗,如跨鐵路橋梁、交通要道上的橋梁等,且荷載試驗費用大,費時長,因此,采用荷載試驗進行橋梁結構評估的方法在實際應用上受到了一定的限制。

該文以廣州市某立交橋為工程背景,基于模態試驗和仿真分析對結構的計算參數進行修正,并對結構的承載能力進行仿真驗算,從而對橋梁結構的承載能力的鑒定方法進行補充。該方法主要的優點是對交通影響小,費用低且速度快。

2 工程背景

該立交橋位于廣州市中心城區,為連接內環路的一重要出口,交通量很大,且跨越廣深鐵路。該橋建于1986年,是公跨鐵的單層立體橋,為斜支梁橋,斜交角度為58055’35’’,橋梁全長為430 m,其中橋長191.62 m,共計為9孔,即5×18 m+23 m+ 35 m+23 m+18 m。本橋主橋采用(23+35+23)m的單孔雙懸臂剛架加掛梁的結構形式。主跨35 m由2邊跨23 m變截面剛架各挑出6.76 m懸臂,兩懸臂間掛21.48 m預應力混凝土組合空心板式梁組成。

剛架橋截面采用變截面變高度多箱室箱梁,梁寬22 m,箱室高度由1 m變化到1.8 m；21.48 m掛梁采用梁高0.9 m的預應力混凝土組合空心板式梁。下部結構采用大懸臂隱式帽梁變截面薄腹橋墩,樁基為鉆孔灌注樁。

原設計荷載為汽-20,掛-100。主橋結構簡圖如圖1所示。

3 橋梁的自振頻率的計算機仿真求解

3.1 成橋時自振頻率求解［2］

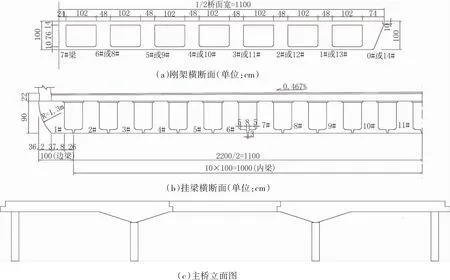
圖1 主橋結構簡圖

在工程技術領域中的很多力學問題和場問題,雖然人們已經得到了它們的基本方程和邊界條件,但能通過解析方法去求解的僅是少數方程性質比較簡單、邊界條件規則的問題,而絕大多數的方程沒有解析解。要解決這類問題的方法有兩種,一種是引入簡化假設,使問題的方程簡單化從而能夠用解析的方法求近似解,但這種方法通常并不可行,甚至得到錯誤解答。另一種方法是保留問題的復雜性,利用數值分析的方法求得問題的近似數值解,當單元劃分合理時,這種數值解具有滿足工程要求的足夠精度。

本文采用大型有限元計算軟件ANSYS,建立了該立交橋動力特性的三維有限元計算模型。在該橋三維有限元計算模型中,主要考慮了如下的建模要點：

(1)將梁部、橋墩等處理成beam188單元。

(2)由于結構的振動特性主要由結構的質量和剛度決定,故必須精確地模擬構件的剛度和質量。

(3)對于縱梁而言,梁單元的剛度即為縱梁本身的剛度,但梁單元的質量為橋面系的所有質量,除了縱梁本身的質量外,還包括了橫隔板、橋面鋪裝、欄桿、人行道、燈柱等,均以線密度的形式計入。

(4)縱橋向用彈簧單元來模擬伸縮縫的影響。

(5)剛架橋與異型掛梁通過主從約束進行連接。

(6)簡支梁與橋墩通過節點耦合的方式達到約束作用。

(7)考慮到埋土深度較大,墩底與地面彈性固結。

(8)立交橋的材料模型：剛架橋、箱梁梁體及橋墩均采用30號混凝土,21.48 m預應力混凝土組合空心板式掛梁梁體采用45號混凝土,預制塊件為25號混凝土,剛架橋及掛梁橋面鋪裝均為30號混凝土。

圖2為全橋的ANSYS模型圖。

圖2 全橋的ANSYS模型圖

對以上的模型進行動力分析,得到全橋的自振頻率及相應的振型,表1列出其前三階的計算結果。

表1 成橋時橋梁的前三階振型

3.2 模態試驗

通過對脈動信號進行譜分析,得出全橋豎向振動頻率為3.33 Hz,測點分別位于兩邊跨的跨中及中跨掛梁的中部,三個測點所測得的數據完全一致。這也是最重要的一個振形,因為它反映了該橋的豎向承載剛度,也就是主梁的剛度,這也是我們在下一階段的計算機仿真分析中參數修正的重要依據；縱橋向振動頻率因為行車干擾較大,不甚明顯,且縱向自振頻率主要反映橋墩的剛度,主梁彎曲剛度對其影響較小；因為橋梁較寬,且墩截面較寬,橫橋向振動不明顯。

表2 模態試驗實測橋梁的前三階振型

3.3 橋梁自振頻率的仿真求解［3-4］

3.3.1 橋梁自振頻率的影響因素分析

混凝土橋的動力特性主要受跨度、截面尺寸、混凝土彈性模量、邊界約束條件、墩高與墩剛度等因素的影響,這里我們以各參數的設計值為基準值1,通過變化有關參數的取值,研究橋梁的動力特性變化趨勢。

(1)混凝土彈性模量E

單純改變混凝土梁的彈性模量(保持其它參數不變),取彈性模量設計值為1,有限元分析結果見圖3。由圖3可見,豎向與橫向頻率隨彈性模量變化比較顯著,而縱向頻率的改變有限。當彈性模量提高到設計值的10倍時,豎向基頻增加約110%,橫向基頻增加約106%,縱向基頻增加約10%。

(2)梁裂縫的影響

混凝土都是帶裂縫工作的,裂縫的存在和發展,使相應部位構件的承載能力受到一定程度的削弱,同時裂縫還會引起保護層剝落、鋼筋銹蝕、混凝土碳化、持久強度低等,甚至危害橋梁的正常運行和縮短其使用壽命。

在有限元分析時,裂縫的影響簡單考慮為削弱截面尺寸。同時改變混凝土梁截面頂底板的厚度(保持其它參數不變),取截面尺寸的設計值為1,有限元分析結果見圖4。由圖4可見,豎向頻率隨截面厚度變化各階的反應不同,基頻是下降的,而其余頻率基本不變；橫向頻率和縱向頻率是明顯降低的,這表明增加梁頂底板厚度對梁剛度的貢獻要小于結構自重的影響。

(3)橋梁縱向約束彈簧剛度

橋梁兩端基本都存在伸縮縫,相當于在橋梁兩端對橋施加一定的縱向約束。很明顯,如果在有限元計算中不考慮縱向約束的影響,直觀概念上將會導致縱向頻率計算的偏差。在ANSYS有限元模擬中,可以通過增加接觸彈簧單元來模擬縱向伸縮縫,通過改變彈簧單元剛度,可以考察伸縮縫的影響(見圖5)。由圖5可知,增加縱向約束彈簧,對豎向和橫向各階頻率沒有任何影響,但是可以顯著增加縱向頻率。彈簧剛度增加10倍,縱向頻率增加了53%。

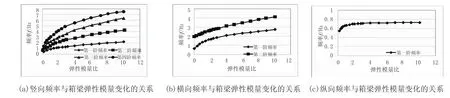
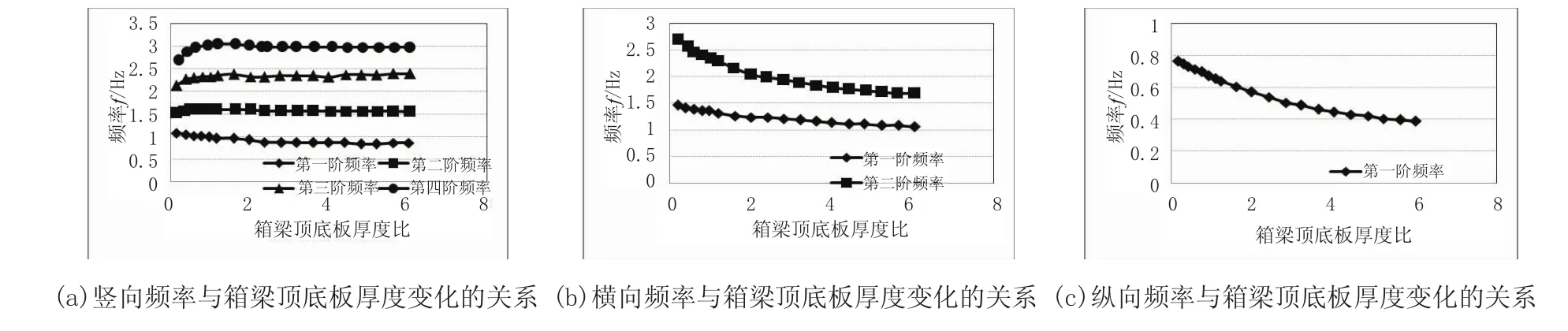
圖4 頻率與梁頂底板厚度變化的關系

圖5 頻率與縱向約束彈簧剛度變化的關系

由上述分析可知,梁混凝土彈性模量對三個方向振動最敏感,縱向約束只改變縱向頻率,增加梁頂底板厚度只會降低基頻。

3.3.2 橋梁自振頻率的修正

由現場實測結果可知,該橋在運營近30年后,混凝土的強度有了較大的變化,具體情況如下：現澆段和橋墩處混凝土實測強度為43.33 MPa,掛梁處混凝土實測強度為57.35 MPa；橋梁外觀上觀測顯示,瀝青鋪裝層基本完好,梁部由于涂抹水泥砂漿,裂縫觀測不是很清楚,但從已經觀測出的預制梁側面網狀裂紋情況,可以推斷該橋存在較大面積的裂紋。再結合以上的自振頻率的影響因素分析,本文對已建的ANSYS模型進行了如下的修正,主要有：

(1)根據實測所得混凝土的強度,得出其相應的彈性模量,修正材料特性。根據經驗公式(1)可求出不同部位混凝土對應的彈性模量。

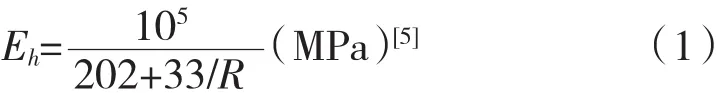
原來30號混凝土現在的彈性模量為3.376 × 1010Pa,原來45號混凝土現在的彈性模量為3.603 × 1010Pa。

(2)根據裂縫開展情況,對截面進行修正,即將部分截面適當削弱,通過調整部分截面質量線密度來保持橋梁的質量不變。

(3)降低縱向約束彈簧的剛度。

由此,重新計算經過修正的模型,該立交橋的修正后的自振頻率如表3所示。

表3 修正后的橋梁前三階振型

對比表2及3可以看出,經過修正后的橋梁前三階理論計算頻率與實測頻率非常接近,說明仿真分析的結果是理想的,可以用于結構的承載力驗算。

4 主橋承載能力驗算及評估［6]

在該橋的承載力驗算中,由于是對舊橋進行承載能力評估并結合目前的交通狀況,故在計算中汽車荷載偏安全的按照城市-A級考慮,按照規范考慮了兩種組合：

工況1:不考慮收縮、徐變,結構升、降溫,頂板升溫,基礎沉降,活載為城-A+人群荷載或掛-120。

工況2:考慮收縮、徐變,結構升、降溫,頂板升溫,基礎沉降,活載為城-A+人群荷載或掛-120。

限于篇幅,這里只列各工況的計算結果。

(1)工況1：斜墩支點處最大負彎矩截面承載極限狀態下截面抗力部分梁不能滿足要求,但是超出量并不大；而跨中截面則截面抗力比荷載效應不利組合相對大比的較多,富余量較大；正墩附近截面抗力則相對斜墩富余量大,相對跨中富余量小；對于21.48 m掛梁,跨中截面下緣沒有出現拉應力。總體上講,主橋在工況1下受力良好。

(2)工況2：斜墩支點處最大負彎矩截面承載極限狀態下截面抗力已經不能滿足要求,且超出比較大；而跨中截面抗力仍然有富余,但是富余量并不大；正墩附近截面抗力富余量也不大；對于21.48 m掛梁,跨中截面下緣沒有出現拉應力。總體上講,主橋在工況2下斜墩頂出現截面抗力不滿足要求,而跨中截面和正墩墩頂抗力富余量不大,其余截面受力良好。

(3)雖然現場發現牛腿部分有一些隱患,但是通過對牛腿的仿真分析結果上來看,強度是滿足受力要求的,且有較大的富余,對此部位以后在運營過程中要長期觀測,對出現的問題要及時解決。

5 結語

本文通過對廣州市一座舊橋采用仿真分析和模態試驗研究,簡要闡述了基于模態試驗和仿真分析相結合的方法在橋梁承載能力鑒定中的應用,從而對橋梁結構的承載能力的鑒定方法進行補充。尤其是在對跨越鐵路、交通量很大的橋梁的承載力進行鑒定時,由于很難采用荷載試驗的方法,采用該方法具有顯著的優點。

［1］ JTG/T J21-2011,公路橋梁承載能力檢測評定規程［S］.

［2］ 李德葆. 試驗模態分析及其應用［M］.北京：科學出版社，2001.

［3］ 張德文，［美］魏阜旋.模型修正與破損診斷［M］.北京：科學出版社,1999.

［4］ 朱晞，朱東生.診斷橋墩損傷參數識別法的研究［J］.蘭州鐵道學院學報,1995(1)：1-7.

［5］ 過鎮海.鋼筋混凝土原理［M］.北京：清華大學出版社,2013.

［6］ JTG D62-2012，公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.

U441+.4

B

1009-7716(2015)09-0083-04

2015-04-10

劉菊玖(1968-),男,湖北漢川人，高級工程師,現從事橋梁檢測與加固設計工作。