基于姿態可操作度的機械臂尺寸優化方法

賈世元，賈英宏，徐世杰

(北京航空航天大學 宇航學院，北京100191)

機械臂的設計有多種準則，大多數機械臂是在運動學可逆的情況下設計的.許多學者，如Roth和Lee等［1-2］最早開始分析機械臂的工作空間，并將其作為機械臂設計準則.文獻［1］討論了給定結構下機械臂工作空間的形狀，以及根據工作空間的形狀，如何設計機械臂的結構.Bergamaschi等［3］提出了一種計算工作空間邊界的方法，并以工作空間的體積為目標函數，優化了3R型機械臂.Snyman等［4］為確定平面機器人工作空間的邊界，提出了一種數值優化算法，計算了平面Stewart平臺和具有冗余串聯機械臂的工作空間.在工作空間的基礎上，Klein和 Yoshikawa等［5-6］學者，最早考慮并定義機械臂的靈巧度和可操作度指標.平面機器人的靈巧度一般用“轉角范圍法”［7］表示，空間機器人的靈活度通常采用“工作角法”［8］和“立體角法”［9］表示.Gosselin 和 Angeles［10］則將機械臂雅克比矩陣的條件數作為首要考慮因素進行機械臂設計，雅克比矩陣的條件數作為設計準則滿足了機械臂設計運動學可逆性要求，同時也為優化機械臂的路徑規劃提供了依據，但它并不適合作為機械臂設計的全局性能指標.Gosselin和 Angeles［11］又提出了將雅克比矩陣條件數和工作空間相結合的機械臂設計全局條件指標(Global Conditioning Index，GCI)，GCI是一種基于雅克比矩陣條件數在整個機械臂工作空間上分布的性能指標，它可以在整個工作空間上衡量機械手的運動學可逆性.文獻［12］采用基于各向同性條件數為目標函數，優化機構參數以最大化其運動學性能;文獻［13-15］以局部條件指標［13］或全局條件指標［14-15］為設計準則，優化設計不同構型的機械臂;文獻［16］對傳統的雅克比矩陣、可操作度及條件數等優化指標的意義及不足做了進一步的闡述.另外，文獻［17］提出了一種基于任務導向的可操作度指標，該指標是任務點處期望可操作性橢球和實際可操作性橢球之間的相似性.

隨著工業機器人及空間機器人任務要求的不斷提高，為滿足機械臂執行多任務的要求，使機械臂具有更好的通用性，機械臂的靈活性和可操作性顯得尤為重要.本文在基于以上設計指標的基礎上，引入“工作球”［7］的概念，定義了靈活性數值指標，以及姿態可操作度的算法，提出一種基于機械臂姿態可操作度的尺寸優化方法.靈活性的數值定義能夠體現出機器人末端作用器位置和姿態在理論上的存在性，且優化指標容易求取，優化算法能夠實現機械臂的全局優化.

針對某一構型的機械臂，利用逆運動學算法求得機械臂的單點靈活性，所求得的靈活性體現出了機械臂工作球上姿態的存在性;在靈活性指標的基礎上，繼而求得機械臂的姿態可操作度值，以姿態可操作度倒數為目標函數利用遺傳算法對機械臂結構參數進行優化，并繪制了優化前后機械臂的靈活性工作空間圖，優化后的機械臂能夠在可達空間中具有較好的可操作性;且優化后較優化前機械臂可操作性得到了明顯的提高.

1 靈活性以及姿態可操作度的定義

機器人的靈活性可用姿態概率系數來表示.以圖1所示的機械臂為例，R1、R2和R3為機械臂的前3個回轉關節，后3個關節可以看成一個球鉸，其球心在腕點Pw，末桿繞球鉸轉動即可實現后3個關節的運動.此時引入“工作球”的概念，在該機械臂工作空間內設立直角坐標系S(Oxyz)，P1(x1，y1，z1)為工作空間中某一工作點，以該工作點作為球心，以末端桿長為半徑，所作的球為“工作球”.在理想情況下，當機械臂運轉時，其腕點Pw可以到達該球面上的任意點，并使末桿通過該點到達工作點P1.但實際上，由于結構上的限制，腕點只能到達球面上的一定區域，該區域越大靈活性越好.在球面可達區域上采用數值離散點定義靈活性，表示該類機器人靈活性指標可用姿態概率系數φ表示，計算工作點P1靈活性時，在“工作球”上隨機取N個均勻樣本點，腕點能通過隨機均勻樣本點使末端點到達工作點的個數為n，此時定義姿態概率系數φ為

圖1 機器人末桿“工作球”Fig.1 “Working sphere”of robot end-effector

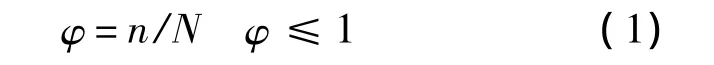
由式(1)可知φ值越大，機器人靈活性越好，當φ=1時，機器人靈活性能最好.

根據機器人正向運動學［18］可得

式中:i-1Ti為坐標系Si與坐標系Si-1之間的齊次坐標轉換矩陣;若已知機械臂末端作用器的位置和姿態，即0Tn已知，則由機械臂逆運動學可以求得關節空間中的坐標值，為求解q1，可用［0T1］-1同時左乘式(2)的兩端，得

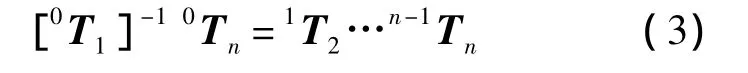
利用兩端對應元素相等，將方程化簡最終求得q1，由此可以得出一般的遞推步驟［4］為

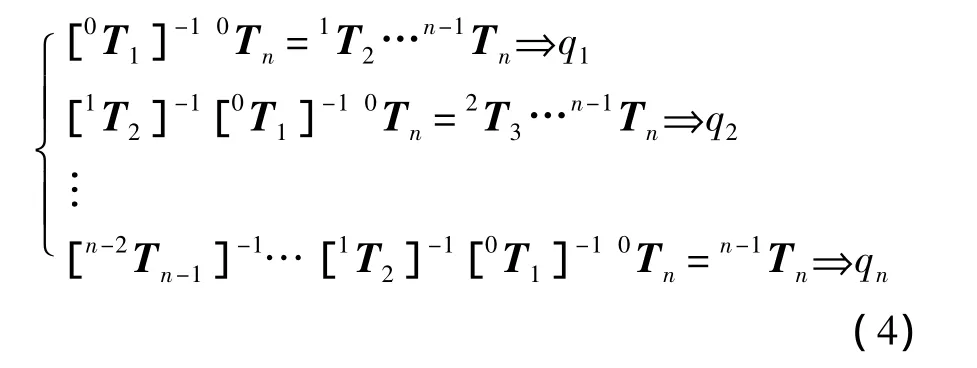
以式(1)的靈活性姿態概率系數只能判斷機器人在某點的靈活性，不能判斷機器人在整個可達工作空間上的整體操作性能，因此在靈活性的基礎上，定義了機器人的姿態可操作度，將可達操作空間中的點離散化，計算每一個離散化的點處的靈活性姿態概率系數值，之后加以統計，最后利用統計的百分比來表征姿態可操作度.即，機械臂可操作度可定義為一個標量指標λ(α)≤100%，其中0＜α≤1，α為姿態概率系數φ的值.姿態可操作度的意義就為:姿態概率系數大于α的工作空間占整個工作空間體積的百分比.例如，λ(0.75)=90%表示姿態概率系數α值大于0.75的工作空間占整個工作空間體積的百分比為90%.顯然，這個指標越大，機械臂整體可操作性越好.

機械臂可操作度指標的計算方法為

式中:m為工作空間中所取樣本點φ＞α的點的個數;M為工作空間中所取均勻樣本點的個數.

2 機械臂尺寸優化算法流程

將機器人的尺寸優化問題轉化評價函數J(h)最小值求解問題，性能指標為機器人姿態可操作度的倒數:

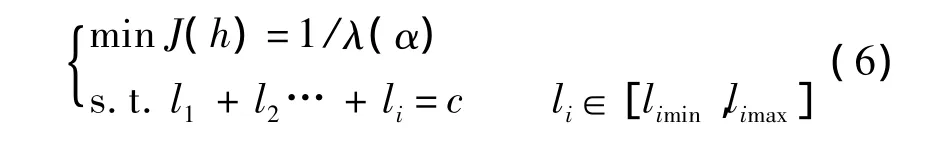
式中:c為機械臂優化桿長參數之和;［limin，limax］為桿長li的優化長度范圍，i為桿序號.

機械臂尺寸優化算法流程圖如圖2所示.

優化算法包括6個部分:

1)初始化種群，設定尺寸參數分布范圍及參數滿足的要求，設置進化代數計數器ig←0;設置最大進化代數I;生成K個體作為初始種群P(0)，其中I和K均為常數，且初始尺寸參數作為初始種群中的一個個體.

2)機器人末端作用器工作點及姿態生成，在工作空間區域內隨機生成M個工作點，在每個工作點上生成一個“工作球”，在“工作球”上隨機選取N個點，工作球上的一個隨機點到工作點的指向即為一個姿態.

3)當機器人的末端作用器在期望位置和姿態時，運用逆運動學算法求解機械臂各個關節角的值.

4)計算性能指標，對每個工作點根據逆運動學算法求得其姿態概率系數，對姿態概率系數大于α的工作點進行統計，得到機械臂在整個工作空間上的姿態可操作度，繼而取姿態可操作度的倒數為性能指標，計算出整個種群中的個體評價函數.

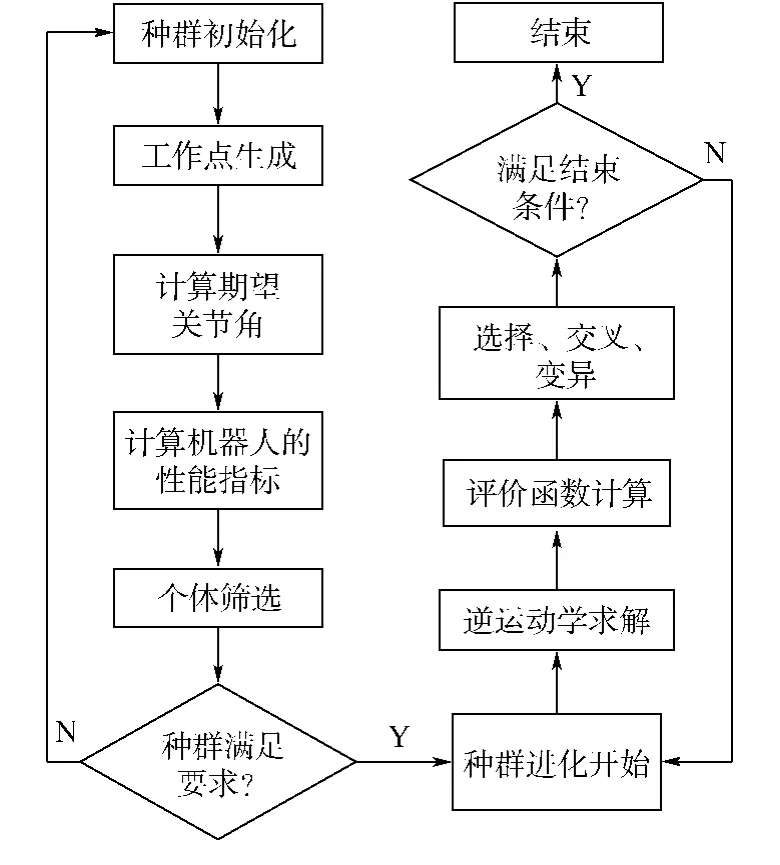
圖2 機械臂尺寸優化算法流程圖Fig.2 Flow chart of dimensions optimization algorithm for manipulator

5)種群進化，在完成評價函數計算后對種群內個體進行適應度評價，然后選擇個體進行交叉和變異操作，交叉算子和變異算子均采用固定值交叉概率和變異概率.

6)終止條件的判斷.若 ig＜I，則 ig←ig+1，進化到下一代;若ig≥I或ig＜I但滿足設定終止條件，則輸出最終解，終止計算.

3 機械臂尺寸優化算法示例

圖3為本文應用對象機械臂結構簡圖及桿件坐標系圖.其中lm和ln為相鄰桿間距.

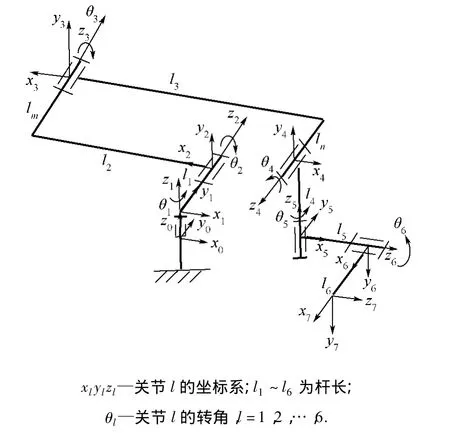
圖3 機械臂結構簡圖Fig.3 Structure schematic diagram of manipulator

由正向運動學式(2)可以求得機械臂末桿位姿矩陣［18］為

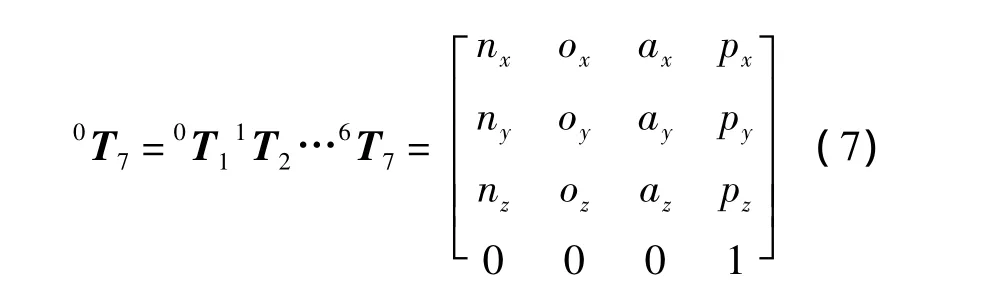
式中:向量 n=［nxnynz］T為法線矢量;o=［oxoyoz］T為方向矢量;a=［axayaz］T為接近矢量，3個矢量分別描述機器人末端操作器的姿態;矩陣0R7=［n o a］為坐標系S7相對基礎坐標系S0的旋轉變換矩陣;p=［pxpypz］T為坐標系S7的坐標原點o7在基礎坐標系S0中的位置矢量.

若已知末桿某一特定的位姿矩陣，為了求解關節角 θ1，根據遞推式(4)可用［0T1］-1同時左乘式(7)得

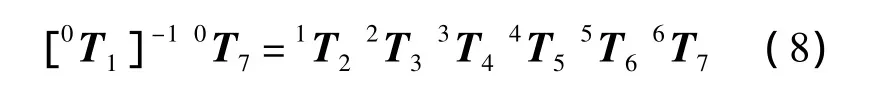
化簡式(8)得

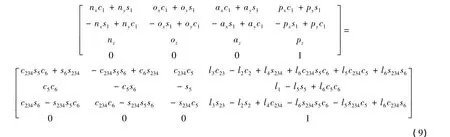
式中:ci=cos θi;si=sin θi;θijk= θi+ θj+ θk，θi、θj和θk分別為第i、j和k個關節的轉角;lj為第j節桿的長度.

將式(9)左側第2行第1列、第3列代入方程右側的第2行第4列并化簡得

式中:k1=l5ax+l6nx-px;k2=-l5ay-l6ny+py;k3=l1.

由式(9)左右兩側對應的第1行第3列，第3行第3列分別相等，利用雙變量反正切函數可以求得

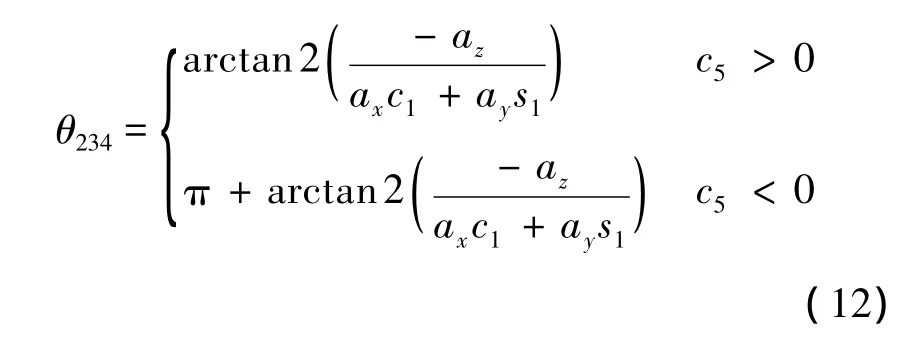
由式(9)左右兩側對應的第2行第1列、第2列分別相等有

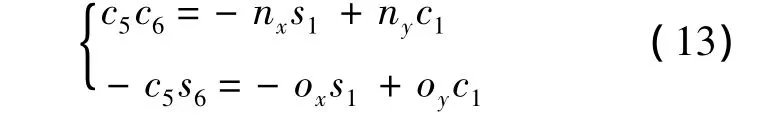
可以求得

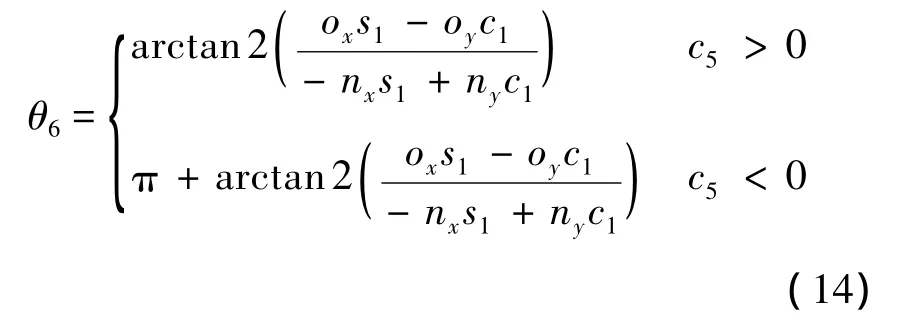
式(13)中第1式兩邊同乘以c6、第2式兩邊同時乘以s6并相減得

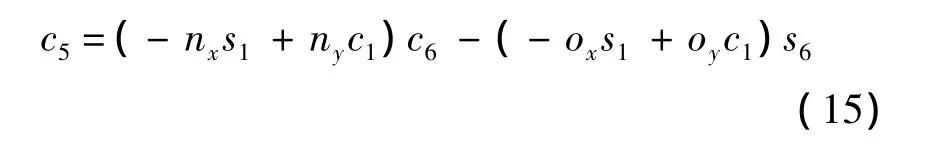
將式(9)中左側第2行第1列代入到右側第2行第4列化簡可以求得

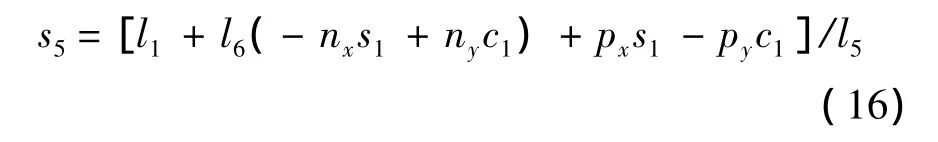
由θ5的正弦和余弦值，利用雙變量反正切函數可以求得

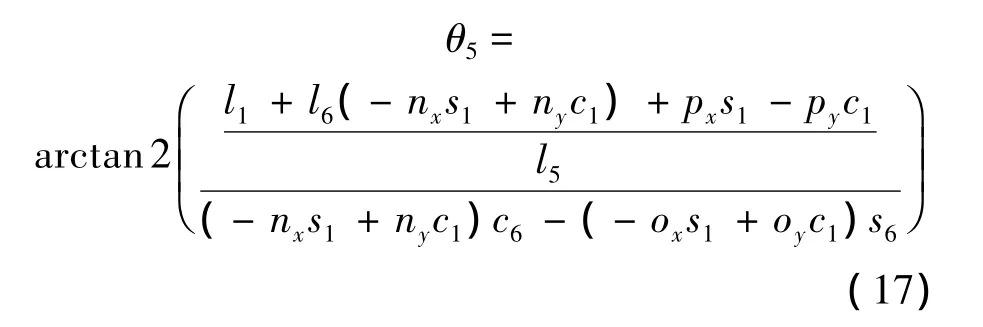
為了 求 θ2，根 據 遞 推 式 (4)，可 用［1T2］-1［0T1］-1同時左乘式(7)得

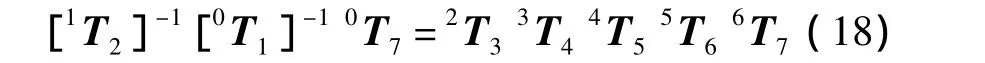
將式(18)中左右兩側矩陣中對應位置的對應元素相等可以推導出:

式中:

繼而可以求得

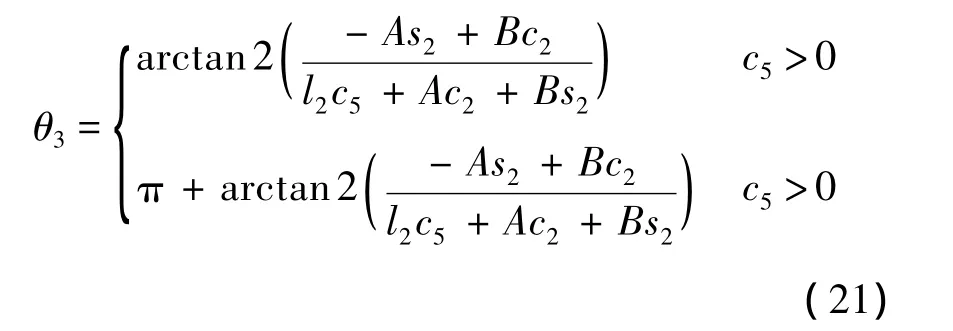
由式(12)、式(19)及式(21)可以求得

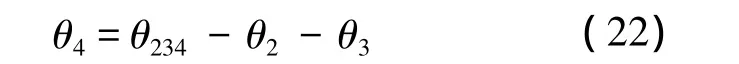
機械臂給定一種工作點位置和姿態后，利用逆運動學對該工作點位置的隨機姿態判斷關節空間中的解是否存在，從而求得單點靈活性的姿態概率系數，繼而可以求得機械臂工作空間中的姿態可操作度.

為保持機械臂結構原有的特征，不改變機械臂的自由度布局，選擇機械臂的桿長參數作為優化設計變量，則機械臂結構參數矩陣為

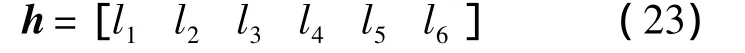
式中:l1～l6均為設計參數，與機械臂對應關系如圖3所示，設計優化參數范圍為 l1∈［0，0.5］，l2∈［0，1.0］，l3∈［0，1.0］，l4∈［0，0.5］，l5∈［0，0.5］，l6∈［0，0.5］，任意選擇一組優化初值為h0=［0.12 0.4 0.9 0.1 0.1 0.15］，初始種群個數20，最大進化代數為100，交叉概率0.8，變異概率0.2，優化過程中工作點M的取值為工作空間中的均勻樣本點，其具體值為M=1 200，每個工作點對應的工作球球面上所取的均勻樣本點為N=600，為使工作點的姿態概率系數α≥0.75，則n≥450，優化前工作點滿足姿態概率系數要求的點的個數為m=608，優化算法結束條件為適應度函數的平均變化小于10-4，適應度函數為

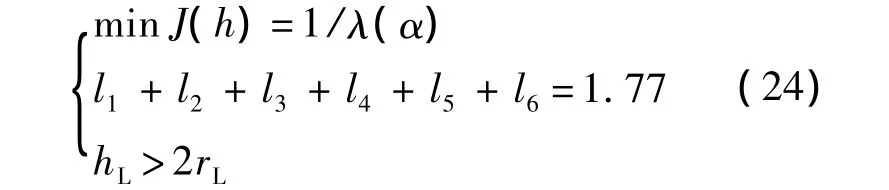
式中:hL為避免機械臂自身碰撞的最小安全距離;rL為機械臂連桿半徑.優化后結果如圖4、圖5所示，圖4所示為適應度函數曲線，圖5所示為桿長參數曲線，其中lk0和lk分別為連桿優化前后的桿長參數.

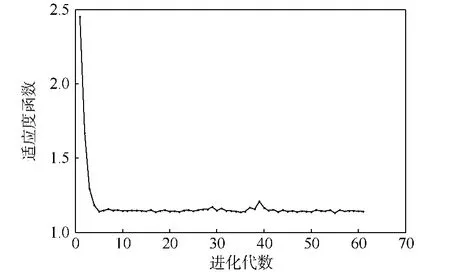
圖4 適應度函數曲線Fig.4 Curve of fitness function

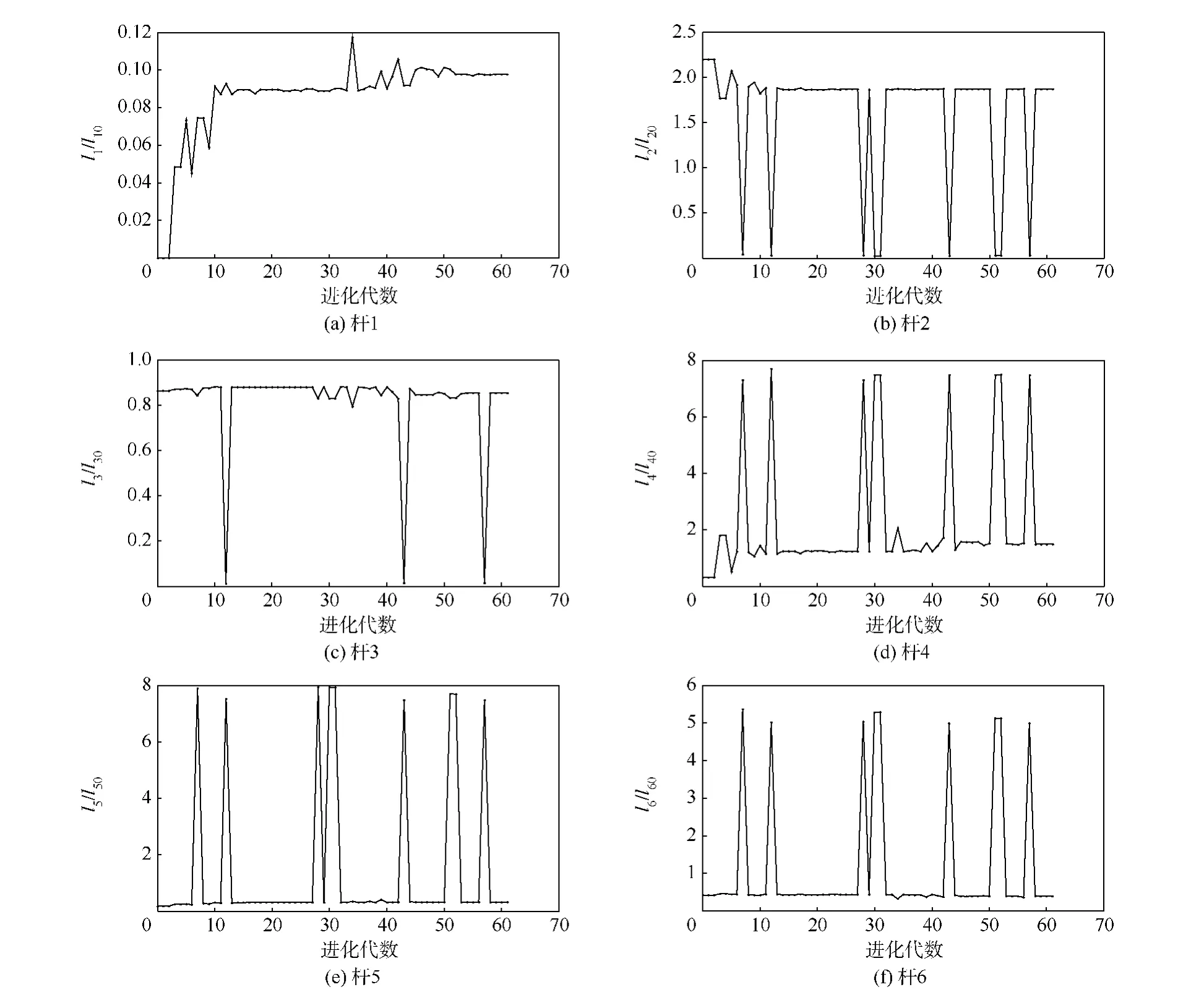
圖5 桿長參數曲線Fig.5 Parameter curve of link length

算法實際進化代數為61代，桿的最終優化尺寸參數為 h'=［0.012 0.749 0.768 0.149 0.033 0.059］;優化后滿足姿態概率系數的工作點的個數為m'=1092，則優化前和優化后姿態可操作度為

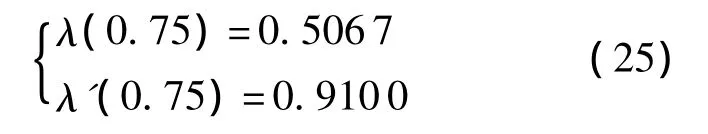
由優化結果可以看出l1桿縮短，優化后長度接近于零;l2桿長度增長，l3桿長度縮短，優化后l2和l3桿的長度基本相同;l4桿長度增長，l5桿和l6桿長度縮短.機械臂設計時短桿的長度應盡量縮短，整部機械臂可以看成由兩節大臂以及多節小臂組成，整體構型類似于人的手臂.

優化前后機械臂靈活性工作空間圖如圖6(a)和圖6(b)所示.顏色條數值表示工作點姿態概率系數的大小;綠色區域為滿足靈活性要求α≥0.75的工作空間，黃色區域為姿態概率系數0.5＜α≤0.75的工作空間，紅色區域表示姿態概率系數α≤0.5的工作空間.由圖6(a)可以看出優化前，工作空間的邊緣及內部紅色區域較大，靈活性較差;機械臂正上方部分區域為黃色，優化后黃色區域變為綠色區域，且工作空間邊緣及內部綠色區域均增大.

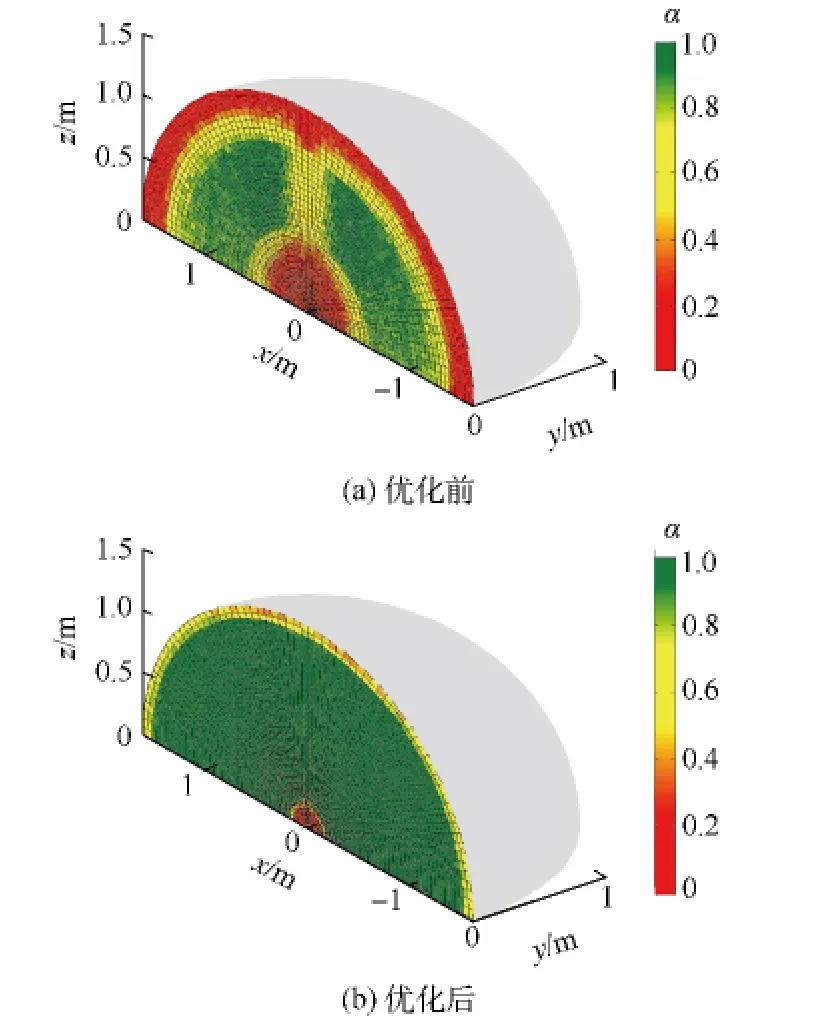
圖6 優化前后機械臂靈活性工作空間圖Fig.6 Spatial graph of dexterous workspace of manipulator before and after optimization

其他初始條件不變的情況下，討論優化算法中姿態概率系數αopt取值大小對結果的影響，針對機械臂靈活性而言，末端作用器可行姿態應達到一定范圍.因此，αopt的取值應大于0.5，否則算法的研究將不具有實際意義.優化算法中對αopt取表1中數值進行優化，其優化結果如表1中h'所示，優化后不同姿態概率系數下的姿態可操作度值如表2所示.

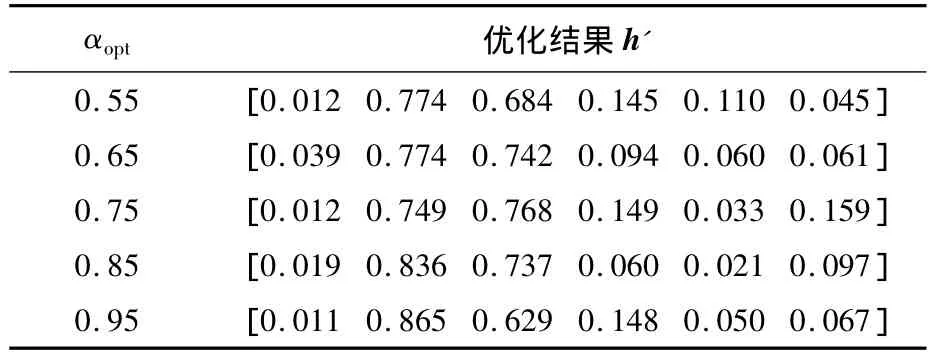
表1 不同αopt取值的優化結果Table 1 Optimal results of different values of αopt

表2 優化后不同α下的姿態可操作度值Table 2 Posture manipulability value of different α after optimization

從表1可以看出，優化算法中不同姿態概率系數下的優化結果均趨向于仿人型機械臂，即機械臂均由兩節大臂和多節小臂組成;從表2可以看出，優化算法中姿態概率系數αopt取值為0.55、0.65和0.75時，優化結果在相應的姿態概率系數下能夠得到較高的姿態可操作度值，當αopt增大到一定程度，優化后姿態可操作度值會逐漸降低，這與實際情況是相符的;但優化結果在姿態可操作度λ'(0.75)下評價時，可以看出優化結果h'(0.55)和 h'(0.95)相對較差，而優化結果h'(0.75)最好，要使優化結果在不同α下均具有相對較高的姿態可操作度，則αopt的取值不能太小也不能太大;另外算法采用數值仿真，αopt的取值太大，算法容易出現失真，因此優化算法中αopt的一般取值范圍為［0.7，0.85］.

4 結論

本文給出了靈活性的數值計算方法，在靈活性的基礎上提出了一種新的姿態可操作度的概念;以姿態可操作度的倒數為適應度函數，利用遺傳算法優化了機械臂的尺寸參數，使優化后的機械臂靈活性達到最優，優化結果可以得出:

1)機械臂的設計類似于人的手臂，由兩節長臂及若干節短臂組成，且兩節長臂的長度相差不大.

2)末端作用器的長度越短機械臂的靈活性越好，因此在設計機械臂時應盡量使短臂桿縮短，甚至可以設計為零桿.

3)優化后的機械臂靈活性較優化前的靈活性提高了40.33%，由此驗證了所提出的機械臂尺寸優化算法的合理性和有效性.

4)該算法中還可以加入不同約束條件實現對機械臂的尺寸優化;還可以實現機械臂的設計-優化-再設計-再優化以獲得靈活性較高的機械臂布局構型.因此，本文提出的機械臂尺寸優化方法在工程上具有實用價值.

References)

［1］ Gupta K C，Roth B.Design considerations for manipulator workspace［J］.ASME Journal of Mechanisms，Transmission，and Automation in Design，1982，104(4):704-711.

［2］ Cwiakala M，Lee T W.Generation and evaluation of a manipulator workspace based on optimum path search［J］.ASME Journal of Mechanisms，Transmission，and Automation in Design，1985，107(2):245-255.

［3］ Bergamaschi P R，Nogueira A C，Saramago S F P.Design and optimization of 3R manipulators using the workspace features［J］.Applied Mathematics and Computation，2006，172(1):439-463.

［4］ Snyman J A，du Plessis L J，Duffy J.An optimization approach to the determination of the boundaries of manipulator workspaces［J］.ASME Journal of Mechanical Design，2000，122(4):447-456.

［5］ Klein C A，Blaho B E.Dexterity measures for the design and control of kinematically redundant manipulators［J］.The International Journal of Robotics Research，1987，6(2):72-82.

［6］ Yoshikawa T.Manipulability of robotic mechanisms［J］.The International Journal of Robotics Research，1985，4(2):3-9.

［7］馬香峰.機器人機構學［M］.北京:機械工業出版社，1991:118-126.Ma X F.Robot mechanisms［M］.Beijing:China Machine Press，1991:118-126(in Chinese).

［8］朱建敏，許有恒.機器人工作靈活性的分析方法［J］.上海交通大學學報，1989，23(2):53-60.Zhu J M，Xu Y H.A method for analyzing the dexterity of a manipulator［J］.Journal of Shanghai Jiao Tong University，1989，23(2):53-60(in Chinese).

［9］劉淑春，許紀倩.工業機器人工作空間及靈活性［J］.北京科技大學學報，1989，11(2):142-147.Liu S C，Xu J Q.On the workspace and the dexterity of general industrial robot［J］.Journal of University of Science and Technology Beijing，1989，11(2):142-147(in Chinese).

［10］ Gosselin C，Angeles J.The optimum kinematic design of a planar three-degree-of-freedom parallel manipulator［J］.ASME Journal of Mechanisms，Transmission and Automation in Design，1988，110(1):35-41.

［11］ Gosselin C，Angeles J.A global performance index for the kinematic optimization of robotic manipulators［J］.ASME Journal of Mechanical Design，1991，113(3):220-226.

［12］趙新華，張威.基于條件數的3-RTT并聯機器人參數優化［J］.中國機械工程，2004，15(21):1903-1905.Zhao X H，Zhang W.Parameter optimization of the 3-RTT parallel manipulator based on the conditioning index［J］.China Mechanical Engineering，2004，15(21):1903-1905(in Chinese).

［13］ Toz M，Kucuk S.Dexterous workspace optimization of an asymmetric six-degree of freedom Stewart-Gough platform type manipulator［J］.Robotics and Autonomous Systems，2013，61(12):1516-1528.

［14］ Zhang P，Yao Z Q，Du Z C.Global performance index system for kinematic optimization of robotic mechanism［J］.ASME Journal of Mechanical Design，2014，136(3):1-11.

［15］ Liu H T，Huang T，Mei J P，et al.Kinematic design of a 5-DOF hybrid robot with large workspace/Limb-Stroke ratio［J］.ASME Journal of Mechanical Design，2007，129(5):530-537.

［16］ Merlet J P.Jacobian，manipulability，condition number，and accuracy of parallel robots［J］.ASME Journal of Mechanical Design，2006，128(1):199-206.

［17］ Lee S.Dual redundant arm configuration optimization with taskoriented dual arm manipulability［J］.IEEE Transactions on Robotics and Automation，1989，5(1):78-97.

［18］于靖軍，劉辛軍，丁希侖.機器人機構學的數學基礎［M］.北京:機械工業出版社，2009:278-288.Yu J J，Liu X J，Ding X L.Mathematical foundation of robot mechanism［M］.Beijing:China Machine Press，2009:278-288(in Chinese).

［19］霍偉.機器人動力學與控制［M］.北京:高等教育出版社，2005:23-28.Huo W.Robot dynamic and control［M］.Beijing:Higher Education Press，2005:23-28(in Chinese).