三角形機翼參數化有限元網格劃分與調整方法

許孟輝，邱志平

(北京航空航天大學航空科學與工程學院，北京100191)

三角形機翼(三角翼)是輕型飛機及殲擊機的典型代表構型之一.作為提高設計質量和縮短設計周期的重要途徑，計算機仿真技術及相關軟件系統在三角翼的初步設計和詳細設計中得到了大量應用［1-3］.而當前三角翼結構的有限元建模耗時低效，已成為限制其結構分析、設計與優化整體效率的瓶頸問題之一［4-7］.參數化有限元建模是提高有限元模型構建效率必不可少的手段之一.

MSC.Patran是國際航空航天器結構分析領域的基準軟件，也是工業領域內著名的并行框架式有限元前后處理及分析仿真系統.用戶可利用其強大的 PCL(Patran Command Language)語言［6-14］和編程函數庫將自行開發的應用程序、功能及應特殊要求開發的內容直接嵌入MSC.Patran的框架系統，或單獨使用或與其他系統聯合使用.本文以其為平臺引入三角翼結構的參數化有限元網格快速建立與調整方法，提高結構分析、設計與優化效率.

劉虎等［5-7］研究了機身/機翼結構的參數化幾何建模方法與參數化有限元建模方法，雖可以人工控制有限元節點與單元信息，但機翼結構的參數化有限元建模的前提是實現其參數化幾何建模.舒恪晟等［8］以PCL語言開發了機身結構參數化幾何建模軟件，但并未實現對應有限元建模.陳小前等［9］與何祖平和王德禹［10］在實現結構參數化建模過程中以基于MSC.Patran的參數化幾何建模為輸入，通過網格種子實現結構的有限元建模，無法實現對有限元節點與單元的人工可控.陳博等［11］、匡國強和張曉晶［12］與劉斌等［13］以不同分析目的為指導借助PCL語言實現結構的快速建模與分析，但所提方法無法應用于三角翼結構的參數化有限元建模，并且有限元的節點與單元信息可控性差.為克服結構參數化有限元網格劃分對參數化幾何建模的依賴，并且有效控制有限元節點與單元信息(位置或編號)，本文以典型多梁式三角翼結構為對象探討其參數化有限元網格劃分方法.

1 三角翼及其預處理

三角翼(如圖1所示)結構由主機翼(P11、P12和P13)、前緣襟翼(P2)和內外側副翼(P3和P4)組成，其中主機翼為厚蒙皮多墻式結構，主要包括翼梁、縱墻、翼肋、桁條和蒙皮等結構件.翼梁和縱墻承受機翼總體剪力和彎矩，并通過固支于機身而獲得支反力和支反彎矩;翼肋維持機翼剖面所需形狀，將自身及收集到的氣動載荷傳遞給蒙皮、翼梁/墻腹板組成的翼盒;蒙皮承受空氣動力，并在蒙皮與翼肋有連接的情況下傳遞氣動載荷給長桁和翼肋;桁條承受蒙皮局部氣動力并將其傳遞給翼肋.

由于機翼前后緣的翼型非常薄，腹板單元若按實際取，常常是畸形的，造成剛度矩陣奇異.一般情況下，按照剖面積不變的原則，將平面外形向內適當收縮，而翼型高度略微增加，如圖2所示，滿足剖面積S2+S3=S1.這樣，既不會使剛度矩陣奇異，又不會造成大的誤差［15］.

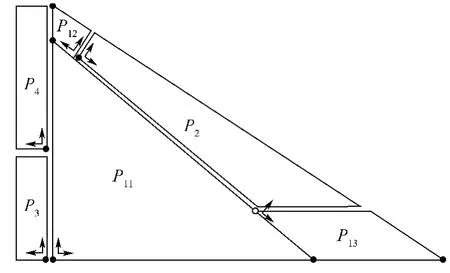
圖1 三角翼示意圖Fig.1 Sketch of a delta wing

圖2 修正原理圖Fig.2 Principle of amendment

通過剖面積等效處理后三角翼結構氣動外形如圖3所示，上下翼面一般為曲面，外形線為曲線時可采用不同精度的分段近似.

本文以圖3所示氣動外形為輸入，考慮方法的通用性，將其劃分為如圖1所示的6個部分，各部分有限元網格獨立建立，最后組成一個完整網格.通過選取表1所列之幾何參數，實現三角翼結構參數化網格劃分與調整.

圖3 氣動外形示意圖Fig.3 Sketch of aerodynamic configuration

表1 幾何參數列表Table 1 Geometric parameters list

2 參數化網格劃分

為滿足對不同精度有限元網格的需求，本文實現機翼展向、弦向和垂向3個方向的單元尺寸的參數化.由于網格單元可以通過節點按照特定順序連接而自動生成，節點的生成與管理是整體參數化網格劃分的關鍵.對于由不同區域有限元網格組合而形成整體有限元網格的大型結構而言，為預防出現編號重復或編號不協調，規定節點與單元的編號格式是非常必要的.同時，滿足一定格式的編號方法對實現節點和單元的管理(如單元分組等)十分有益.

2.1 節點編號定義

節點本質上可視為二維數組，分別存儲節點編號和節點空間位置，其中節點編號規則由設計人員自定義實現，節點空間位置信息由幾何求交運算或數值計算確定.為方便確定三角翼有限元網格的節點空間位置，在不同分區建立適當的局部坐標系，如圖1所示.

根據有限元建模“由大及小劃分，以小代大模擬”的基本思路，圖1中三角翼結構的不同分區可視為一種粗略的有限單元劃分格式.進一步，在不同分區內部，以翼肋為切入點對節點進行編號，通過翼肋與其他各個結構件的相交關系定義節點編號顯示格式:

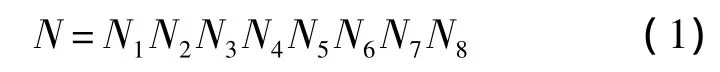
對應的節點編號數值計算格式為

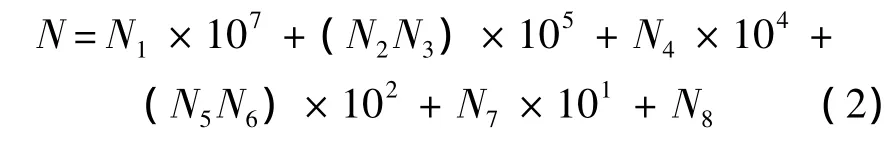
圖4 左側機翼ab梁腹板的節點編號Fig.4 Numbers of nodes on web of beam ab of left wing

式中:N1為機翼位置序號，左側機翼取值為1，右側機翼取值為2;N2N3為不同分區內的翼肋序號.區域P11編號范圍為0～19;區域P12編號范圍為20～29;區域P13編號范圍為30～39;區域 P2編號范圍為40～49;區域P3編號范圍為50～59;區域P4編號范圍為60～69;N4為翼肋間節點序號，取值范圍為0～9;N5N6為不同分區內的梁/墻序號;N7表示梁/墻間節點序號，取值范圍為0～9;N8為上下蒙皮間節點序號，取值范圍為0～9，上蒙皮節點取值為0，下蒙皮節點取值為9，中間節點取值范圍為1～8.

根據式(1)所確定的節點編號格式，圖4給出了左側三角翼ab梁腹板的節點編號.需要注意的是，編號格式中各變量的取值范圍確定了式(1)的實際適用范圍，可根據具體問題予以調整.

2.2 單元編號定義

網格單元通過滿足自定義編號規則的網格節點按一定順序連接而自動生成.根據網格節點編號規則，單元編號顯示格式定義為

相應的數值計算格式為

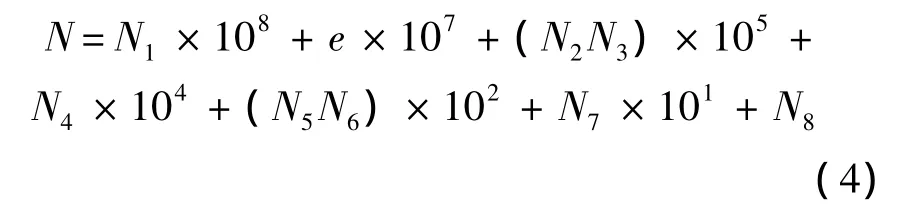
式中:Ni含義與式(1)和式(2)中對應含義相同，i=1，2，…，8;e為單元類型序號，規定:

1)殼單元:蒙皮取值為0，梁/墻腹板取值為1，肋腹板取值為2，斜肋(位于區域 P13和P2)腹板取值為3.

2)桿單元:梁/墻/緣條與桁條取值為4，肋緣條取值為5，斜肋緣條取值為6.

值得注意的是，在三角形單元和四邊形單元過渡區內，為避免單元編號非協調性，本文對三角形單元編號進行了修正，如將單元編號中的N2N3(或N5N6)以N2N3+20(或N5N6+20)代替.

2.3 網格劃分

2.3.1 骨架布局的確定

在自定義氣動外形所對應的主受力盒區P11中，設計人員給定局部坐標系下的梁/墻位置參數及翼肋位置參數，在加工工藝等約束下，需要定義翼肋沿x方向貫穿位置，即通過圖5中y與y1、y2的自定義邏輯關系計算翼肋貫穿位置的x坐標值，以確定機翼骨架幾何布局滿足設計人員的要求.本文引入工藝參數a，通過初步判斷翼肋貫穿截止坐標并依此建立初步有限元網格.借助第2.3.4節網格細化操作可確定翼肋最終的理想貫穿截止位置.

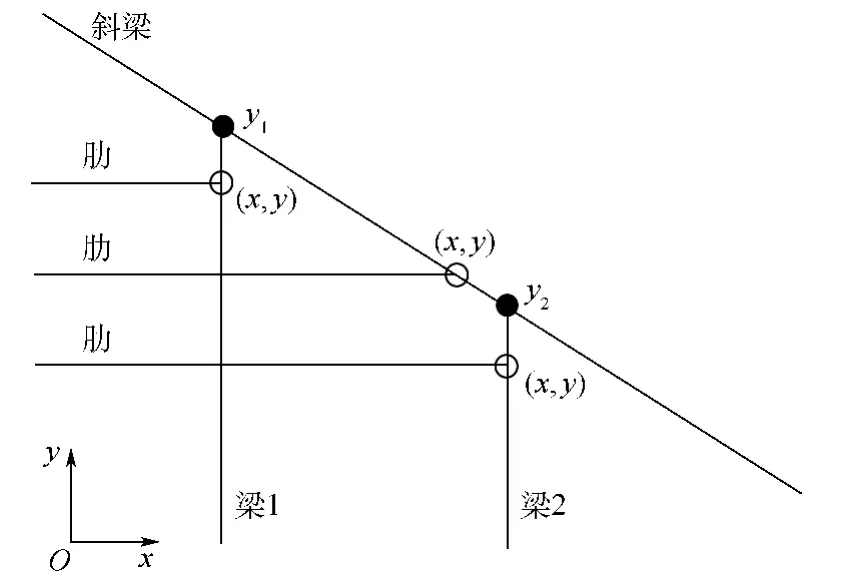
圖5 肋端點位置圖Fig.5 Sketch of rib end locations

2.3.2 節點布置的確定

在給定三角翼所有幾何參數的情況下，其不同分區內由梁/墻、翼肋、桁條等圍成的單位分區主要有5種情形，在上下翼面間的中面處的投影如圖6所示.因此，需要分別確定在此5種不同情形下的節點布置方式.

引入對應骨架布局等邏輯判斷的形狀矩陣M2×5，該矩陣的每一列分別依次存儲從左下角頂點坐標起沿逆時針方向的各頂點坐標，若無對應頂點，則初始化對應元素為0，如圖7所示.

圖6 骨架結構的中面投影單位分區形狀Fig.6 Shapes of unit region of projections of skeleton components on middle plane

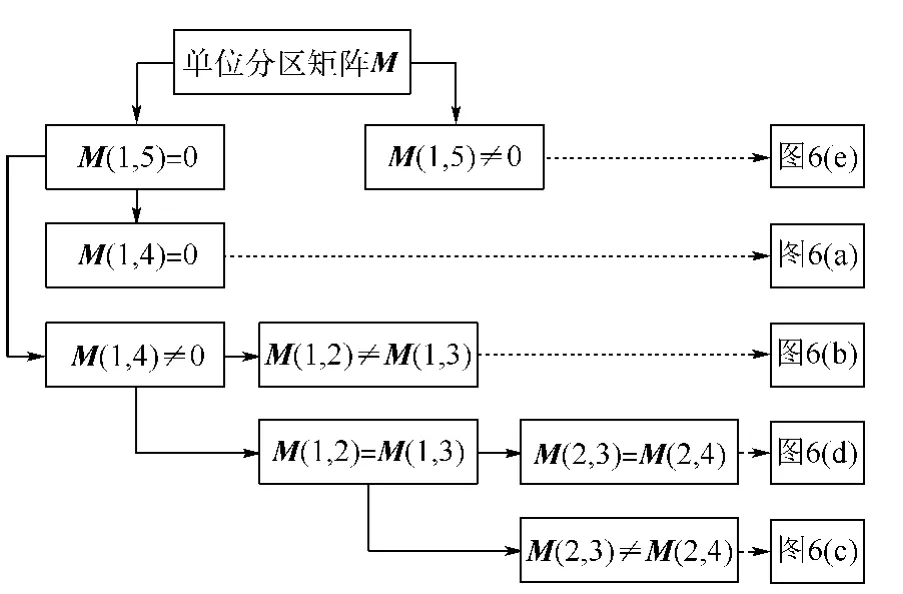
圖7 形狀矩陣與單位分區的關系Fig.7 Relationships between geometrical matrix and unit regions

通過形狀矩陣M確定不同單位分區的節點布置方式.值得注意的是，決定節點間距的單元尺寸是設計人員輸入參數.因此，需要引入非矩形單位分區的節點布置截止原則.以圖6(a)所示機翼中面的三角形單位分區為例，基于弦向單元尺寸由左向右依次布置底邊的節點，當待布置節點與右下角頂點之間的距離滿足一定關系，則待布置節點取作右下角頂點.進一步，以底邊弦向節點為基礎，逐列布置每個底邊節點對應的展向節點，當待布置展向節點與底邊節點對應的斜邊節點(通過底邊節點的垂線與斜邊的交點)之間的距離滿足一定關系時，待布置節點取作底邊節點對應的斜邊節點.而距離關系可以由設計人員通過單元長細比等參數自定義.通過三角翼中面的布置節點投影至上下翼面，并可以根據垂向單元尺寸參數確定腹板位置處的節點，最后將中面輔助節點刪除.

2.3.3 有限元網格劃分

按照指定順序依次連接已有的節點可以生成相應的有限單元并分組，在該過程中通過弦向相鄰2列的節點數目之間的關系確定四邊形單元與三角形單元的具體節點連接方式.對于相鄰單位分區間的單元連接則借助相應形狀矩陣完成.進一步，由式(4)賦予相應單元編號，至此已建立初步有限元網格.根據機身兩側三角翼的對稱性，另一側三角翼的有限元網格可以通過兩機翼間距對稱生成，并賦予相應的節點編號和單元編號.

2.3.4 有限元網格細化

基于已建立的三角翼有限元網格，設計人員可以對其完成進一步細化，以2個梁/墻編號和2個翼肋編號作為參數完成機翼開口設置，以翼肋貫穿位置調整參數確定翼肋理想貫穿位置，以梁/墻編號為參數完成相應的桁條等網格劃分，這些網格細化操作均可以通過刪除已有單元與部分關聯節點完成.

值得注意的是，本文以三角翼結構的有限元網格劃分為重點，不同分區間的連接、單元屬性、邊界條件及載荷等的設置則仍通過MSC.Patran完成.

3 參數化網格調整

在很多情形下，設計人員期望以當前有限元網格為基礎以較小代價完成網格一定幅度的調整.如內/外側副翼中翼肋的位置調整、適應不同飛行狀態的前緣襟翼及內外側副翼等活動舵面的旋轉角度調整等.

3.1 位置調整

內/外側副翼中翼肋的位置調整是通過指定翼肋序號與待移動新位置坐標2個參數完成.值得注意的是:①限于主受力盒區中梁、墻、翼肋間相交的關系復雜，不宜進行翼肋和梁/墻位置的局部調整;②由于結構件的位置調整是通過節點移動完成，為避免引起氣動外形的大幅變化，位置調整僅適用于一定距離內的結構件位置移動.而大幅度的結構件位置調整亦可以通過結構件重新參數化網格劃分完成.

3.2 角度調整

在不同飛行狀態下，前緣襟翼和內/外側副翼的旋轉狀態是不同的.為快速建立不同飛行狀態下三角翼結構的有限元網格，可以通過旋轉角度參數實現活動舵面有限元網格的角度調整.

4 實例

基于所提參數化網格劃分方法，本文借助PCL語言開發了三角翼結構參數化有限元網格劃分模塊，如圖8所示.并對圖3所示的三角翼結構進行參數化有限元網格劃分.

圖8 參數化網格劃分模塊Fig.8 Parametric meshing module

4.1 有限元網格劃分

在給定2種不同的幾何參數與有限元尺寸參數前提下，所生成的三角翼結構初始有限元網格如圖9所示，對應的骨架有限元網格如圖10所示.

在第2種參數設置下，通過給定開口參數、翼肋貫穿位置參數及桁條對應梁/墻序號參數，可以得到細化的骨架有限元網格，如圖11所示.

圖9 情形1和情形2下的機翼有限元網格Fig.9 Finite element(FE)meshing of wing in Case 1 and Case 2

在建立有限元過程中，相應的分組同步完成，如圖12所示.

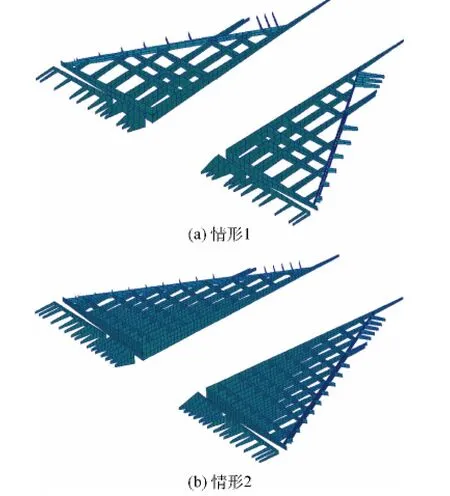
圖10 情形1和情形2下的骨架有限元網格Fig.10 FE meshing of skeleton in Case 1 and Case 2

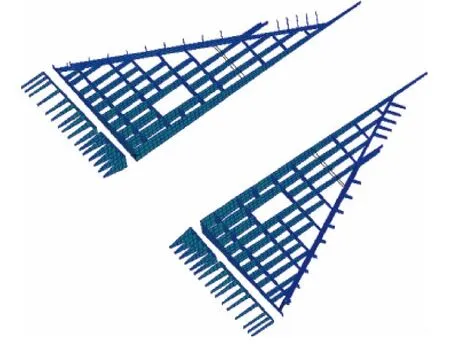
圖11 細化的骨架有限元網格Fig.11 Refined FE meshing of skeleton

圖12 自動分組結果Fig.12 Consequences of auto-group

4.2 有限元網格調整

通過給定內/外側副翼的翼肋序號與待移動新位置參數，可以對相應結構件進行位置調整，如圖13所示.

通過給定前緣襟翼、內/外側副翼的旋轉角度參數，可以建立活動舵面在調整角度后的有限元網格，如圖14所示.

圖13 副翼的肋位置調整Fig.13 Location modifications of ribs of aileron

圖14 舵面的角度調整Fig.14 Angle modifications of control surfaces

5 結論

本文以多梁式三角翼結構為對象探索了參數化有限元網格劃分和調整方法，定義了統一簡潔的有限元節點和單元編號規則，引入翼肋貫穿截止準則及形狀矩陣完成單位分區的有限元網格劃分，通過網格細化完成開口設置、翼肋貫穿截止位置修正及桁條網格劃分，并進一步探索了內/外側副翼的翼肋位置小幅調整及旋轉舵面的角度調整方法.本文探索為三角翼的結構分析與多學科設計優化奠定了基礎，形成具有借鑒意義的結論如下:

1)本文所定義有限元節點與單元的編號規則協調統一實用，便于實現節點和單元的后續操作，如開口設置等.

2)所引入之翼肋貫穿截止準則簡便，綜合網格細化方法，滿足任意輸入參數下機翼內部構型的判斷與修正.

3)所定義之形狀矩陣M有效簡化了有限元節點布置、單元生成及不同單位分區間單元連接，對不同形式的單位分區具有普遍適用性.

4)活動多面的角度調整功能有利于開展不同飛行狀態下的結構分析等;但限于所輸入之幾何氣動外形，內外側副翼的翼肋位置調整適用于小幅調整.

5)由于平直機翼氣動外形相對規則，本文方法適用于平直機翼的有限元參數化網格劃分與調整.

References)

［1］ Roberts R W，Canfield R A，Blair M.Sensor-craft structural optimization and analytical certification，AIAA-2003-1458［R］.Reston:AIAA，2003.

［2］ Mike R.MD Nastran 2006 DMAP programmer’s guide［M］.Spmta Ana:MSC Software Corporation，2005:xii-xiv.

［3］ Hermann T M，Mamarthupatti D，Locke J E.Postbuckling analysis of laminate composites utilizing commercial FEA software，AIAA-2005-0194［R］.Reston:AIAA，2005.

［4］金海波，丁運亮.飛機概念設計中的外形參數化模型的研究［J］.南京航空航天大學學報，2003，35(5):540-544.Jin H B，Ding Y L.Parameterization model for aircraft concept design［J］.Journal of Nanjing University of Aeronautics and Astronautics，2003，35(5):540-544(in Chinese).

［5］白振東，劉虎，武哲.低可探測機身參數化造型與優化［J］.北京航空航天大學學報，2007，33(12):1391-1394.Bai Z D，Liu H，Wu Z.Parametric modeling and optimization of low observability fuselage in aircraft conceptual design［J］.Journal of Beijing University of Aeronautics and Astronautics，2007，33(12):1391-1394(in Chinese).

［6］羅明強，馮昊成，劉虎，等.民用飛機機翼結構快速設計及自動化調整［J］.北京航空航天大學學報，2009，35(4):468-471.Luo M Q，Feng H C，Liu H，et al.Rapid wing structure design and automated scheme adjustment for civil aircraft［J］.Journal of Beijing University of Aeronautics and Astronauctics，2009，35(4):468-471(in Chinese).

［7］羅明強，馮昊成，劉虎，等.機翼結構有限元的快速建模及自動化調整［J］.北京航空航天大學學報，2011，37(6):680-684.Luo M Q，Feng H C，Liu H，et al.Rapid wing structural finite element modeling and automated adjustment［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37(6):680-684(in Chinese).

［8］舒恪晟，金海波，姜琬.基于Patran二次開發的機身結構參數化建模［J］.飛機設計，2011，31(2):30-32.Shu K S，Jin H B，Jiang W.Fuselage structure parametric modeling based on secondary development of Patran［J］.Aircraft Design，2011，31(2):30-32(in Chinese).

［9］許林，郭中全，陳小前，等.基于PCL的高超飛行器結構參數化建模［J］.計算機工程，2008，34(22):1-3.Xu L，Guo Z Q，Chen X Q，et al.Parametric modeling for hyper sonic vehicle structure based on PCL［J］.Computer Engineering，2008，34(22):1-3(in Chinese).

［10］何祖平，王德禹.基于MSC.Patran二次開發的結構參數化建模及其集成開發環境［J］.航海工程，2005(2):17-20.He Z P，Wang D Y.Parameterized modeling based on MSC.Patran and its integrated development environment［J］.Ship ＆Ocean Engineering，2005(2):17-20(in Chinese).

［11］陳博，陳秀華，汪海.MSC.Patran二次開發及其集成開發環境［J］.機械設計與制造，2007(7):71-73.Chen B，Chen X H，Wang H.Redevelopment of MSC.Patran and its integrated development environment［J］.Machinery Design ＆ Manufacture，2007(7):71-73(in Chinese).

［12］匡國強，張曉晶.基于MSC Patran參數化建模的飛艇蒙皮織物面內剛度預測［J］.計算機輔助工程，2009，18(3):42-45.Kuang G Q，Zhang X J.In-plane stiffness prediction on fabric of airship envelop based on parameterized modeling of MSC Patran［J］.Computer Aided Engineering，2009，18(3):42-45(in Chinese).

［13］劉斌，韓慶，鐘小平.基于MSC.PCL的飛機結構穩定性系統開發［J］.科學技術與工程，2010，10(28):7082-7088.Liu B，Han Q，Zhong X P.Development of aircraft structure’s stability system based on MSC.PCL［J］.Science Technology and Engineering，2010，10(28):7082-7088(in Chinese).

［14］ MSC.Patran PCL reference manual［Z］.2007.

［15］葉天麟，周天孝.航空結構有限元分析指南［M］.北京:航空工業出版社，1996:514-515.Ye T L，Zhou T X.Guide for finite element analysis of aerospace structures［M］.Beijing:Aviation Industry Press，1996:514-515(in Chinese).