一類非局部非線性擴散方程解的全局爆破

裴海杰，李中平，楊麗，杜宛娟

（西華師范大學(xué)大學(xué)數(shù)學(xué)與信息學(xué)院，四川南充637009）

一類非局部非線性擴散方程解的全局爆破

裴海杰，李中平，楊麗，杜宛娟

（西華師范大學(xué)大學(xué)數(shù)學(xué)與信息學(xué)院，四川南充637009）

主要研究在Dirichlet邊界條件或Neumann邊界條件下的一類非局部非線性的擴散方程問題.在適當?shù)募僭O(shè)下，證明解的存在性、唯一性、比較原則、以及解對初邊值條件的連續(xù)依賴性，并就給定的初邊值條件，證明解在有限時刻全局爆破.

非局部擴散；Dirichlet邊界條件；Neumann邊界條件；全局爆破

1　引言及主要結(jié)果

主要研究一類帶有Dirichlet邊界條件的非局部非線性擴散方程：

和一類帶有Neumann邊界條件的非局部非線性擴散方程：

其中，J：RN→R是單調(diào)遞減的光滑徑向?qū)ΨQ函數(shù)，滿足

顯然函數(shù)f在有限時刻t=T處爆破.此時，方程（1.1）、方程（1.2）具有爆破邊界條件.過去數(shù)十年里，關(guān)于擴散模型的研究已取得許多重要成果.比如經(jīng)典的熱方程ut=△u，多孔介質(zhì)方程ut=△um（其中m＞1），Non-Newton擴散方程但這些擴散模型都是局部的.有關(guān)局部擴散爆破研究可參看綜述文獻［10-12］及專著文獻［13-14］.

最近非局部方程

被廣泛地應(yīng)用于對非局部擴散模型的描述.正如在文獻［4］中所提及的那樣，如果將u（x，t）看作是某種群在點x處t時刻的密度，J（x-y）是該種群從x點躍到y(tǒng)點的概率分布，那么

文獻［3］中，C.Cortazar等研究了如下Cauchy問題：

其中，核函數(shù)J：R→R為非負的光滑函數(shù)，在區(qū)間［-1，0］嚴格遞增，［0，1］嚴格遞減，且滿足看作是種群在點x處t時刻的密度，為從y點躍到x點的概率分布，那么便是種群從其他地方遷移至x處的速率.與之相應(yīng)的，為種群遷離x到達其他地方的速率.作者證明了問題（1.4）具有自由邊界.

文獻［1］中，Bogoya先后研究了如下三個問題：

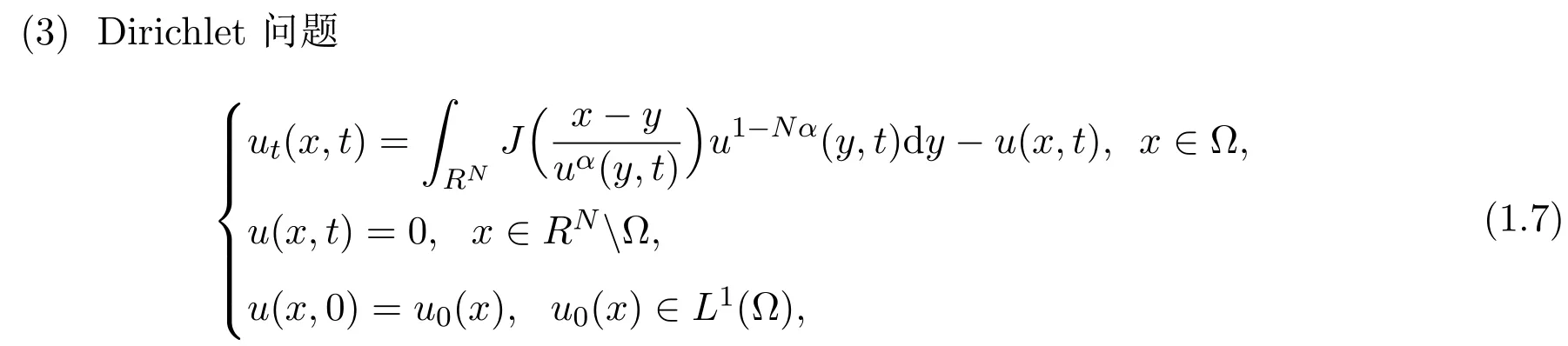
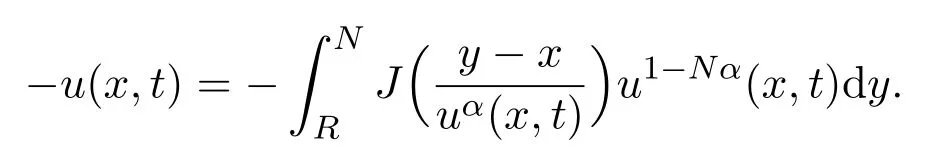
作者證明了對于問題（1.5）：如果初值條件u0（x）是有界的緊支的，那么相應(yīng)的解存在自由邊界.對問題（1.6）：對每一個非負的u0∈L1（?），都存在唯一解，使得u∈C（［0，∞）；L1（?）），而且特別地，如果且那么方程的解在內(nèi)將一致有成立.對問題（1.7）：如果函數(shù)u0是非負有界的，那么方程的解在內(nèi)將一致有成立.

Bogoya在后續(xù)工作中（見文獻［2］），研究了帶有爆破邊界條件的方程（1.1）與方程（1.2），其中爆破條件f=（T-t）-γ.該文證明了，當γ≤1時，解在有限時刻T全局爆破，并給出了爆破速率.

受上述文獻啟發(fā)，研究帶有經(jīng)典對數(shù)形式的爆破邊界條件方程（1.1）與方程（1.2），其中f=-ln（T-t）.與冪級數(shù)形式相比，對數(shù)形式的爆破邊界條件，其最大不同之處就在于，對數(shù)形式的奇異速率要比冪級數(shù)形式的情況慢得多.關(guān)于帶有對數(shù)形式邊界流的擴散方程研究可參看［8-9］及其相關(guān)參考文獻.

現(xiàn)在敘述本文的主要結(jié)果.

定理1.1（解的存在唯一性）設(shè)g0（x）∈L1（?）且是一個非負函數(shù)，那么對一切f∈L∞（（0，∞）；L1（RN?）），如果存在常數(shù)C使得f≥C＞d≥0，那么方程（1.1）與方程（1.2）存在唯一解.

定理1.2（解對初邊值條件的連續(xù)依賴性）設(shè)u（x，t），v（x，t）是方程（1.1）或方程（1.2）的解，相應(yīng)的初始值為u0及v0，且邊界條件分別f1，f2，那么存在一個正常數(shù)C：=C（t0）＞0，對某一確定的t0，有下式成立：

定理1.3（比較原則）設(shè)u（x，t），v（x，t）是方程（1.1）（或方程（1.2））的的兩個連續(xù)解，且相應(yīng)的初始值為u0，v0，以及邊界條件分別f1，f2，如果當x∈?時u（·，0）≤v（·，0），以及對所有的（x，t）∈（RN?）×［0，∞），有f1≤f2成立，那么對一切（RN×［0，∞），有u（x，t）≤v（x，t）.

定理1.4（全局爆破）設(shè)u（x，t）是方程（1.1）（或方程（1.2））的連續(xù)解，f（x，t）=-ln（T-t），則方程的解在有限時刻全局爆破，且

2　定理證明

定理1.1的證明本文將在Banach空間B=C（［0，t0］；L1（?））上證明方程（1.1）解的存在性與唯一性.方程（1.2）解的存在性與唯一性證明與方程（1.1）情形相似，這里不再贅述.

［1］Bogoya M.A nonlocal nonlinear diffusion equation in higher space dimensions［J］.Math.Anal.Appl.，2008，344：601-615.

［2］Bogoya M.Blowing up boundary conditions for a nonlocal nonlinear diffusion equation in several space dimensions［J］.Nonlinear Anal.，2010，72：143-150.

［3］Fife P.Some Nonclassical Trends in Parabolic-like Evolution，in：Trends in Nonlinear Analysis［M］.Berlin：Springer，2003.

［4］Cortazar C，Elgueta M，Rossi J D.A nonlocal diffusion equation whose solution develops a free boundary［J］.Ann.Henri Poincare，2005，6（2）：269-281.

［5］Ignat L，Liviu I，Rossi J D.A nonlocal convection-diffusion equation［J］.Funct.Anal.，2007，251：399-437.

［6］Ignta L，Liviu I，Rossi J D，et al.Decay estimates for nonlinear nonlocal diffusion problems in the whole space［J］.Journal d′Analyse Math′ematique，2014，122：375-401.

［7］Ignat L，Rossi J D，Antolin A S.Lower and upper bounds for the first eigenvalue of nonlocal diffusion problems in the whole space［J］.Differential Equations，2012，252：6429-6447.

［8］Li Z P，Mu C L.Global existence and blow-up analysis for a nonlinear diffusion equation with inner absorportion and boundary flux［J］.Dynamical Systems，26（2）：147-159.

［9］Li Z P，Mu C L.Critical exponents and blow-up rate for a nonlinear diffusion equation with logarithmic boundary flux［J］.Nonlinear Anal.，2010，73：933-939.

［10］Deng K，Levine H A，The role of critical exponents in blow-up theorems：the sequel［J］.Math.Anal.Appl.，2000，243：85-126.

［11］P′erez-Llanos M，Rossi J D.Numerical Approximations for a Nonlocal Evolution Equation［J］.SIAM J.Numerical Analysis，2011，49：2103-2123.

［12］Levine H A.The role of critical exponents in blow up theorems［J］.SIAM Rev.，1990，32：262-288.

［13］Samarskii A A，Galaktionov.V.A，Kurdyumov.S.P，et al.Blow-up in Quasilinear Parabolic Equations［M］.Berlin：Walter de Gruyter，1995.

［14］Wu Z Q，Zhao J N，Yin J X，et al.Nonlinear Diffusion Equations［M］.Singapore：World Scientific，2001.

Global blow-up for a nonlocal nonlinear diffusion equation

Pei Haijie，Li Zhongping，Yang Li，Du Wanjuan

（Department of Mathematics and Information，China West Normal University，Nanchong637009，China）

In this paper，we mainly study a nonlocal nonlinear diffusion equation with Dirichlet boundary conditions or Neumann boundary conditions.Under suitable hypotheses，we will prove existence，uniqueness and the validity of a comparison principle for solutions of these problems，as well as solutions of the problems depend continuously on initial and boundary data.Moreover we will prove that the solution globally blows up in finite time with a given initial and boundary datum.

nonlocal diffusion，Neumann boundary condition，Dirichlet boundary condition，global blow-up elementary method，conjecture

O175.2

A

1008-5513（2015）06-0588-08

10.3969/j.issn.1008-5513.2015.06.006

2015-04-25.

國家自然科學(xué)基金（11301419）；四川省教育廳重點項目（13ZA0010，14ZB0143）；西華師范大學(xué)大學(xué)生科技創(chuàng)新項目（42714081）.

裴海杰（1991-），碩士生，研究方向：偏微分方程.

李中平（1980-），博士，教授，研究方向：微分方程.

2010 MSC：35B44，35B51，35F31